基于马尔可夫模型的电动重载卡车市场需求预测方法

李洪宇,付凤平,张世科

(国网河北省电力有限公司营销服务中心,河北 石家庄 050035)

0 引言

为了维护生态环境,减少对化石能源的消耗,很多车辆使用了绿色能源作为动力,如家用电动汽车、公交车等逐渐采用了电力动力,而且重载卡车进入电动化时代。将电动重载卡车投入市场前,需要详细了解客户对该类产品的需求,并作出产品分析。

现有研究中,文献[1]以TEI@I方法论为主要算法,设计了一个针对于航空客运的产品框架,在分解EEMD时间序列的过程中,基于数据驱动对每个序列之间的关系进行了的分析,并结合计量经济学等相关研究,设计了一套产品预测智能算法。将该方法应用于电动重载卡车,其市场需求预测模型所得到的预测结果较为稳定,但是该方法只能预测短时间内的市场需求,在时间较长的市场需求预测中效果极差。文献[2]为研究了水产品物流资源的合理配置,预测了该产业的冷链需求,基于RBF神经网络模型,设计了一套多元线性回归算法,分别计算了冷链物流的各项需求分析,并对分析结果作出了综合性的总结,得到了一个误差极小的预测模型。将该模型应用于电动重载卡车市场需求预测模型中,可以得到较好的预测精度,但是其需要大量的数据支撑,计算效率较差。

为解决现有方法的不足,本文提出基于马尔可夫模型的电动重载卡车市场需求预测方法,可有效预测电动重载卡车的市场需求,为电动重载卡车行业的规划和发展提供帮助。

1 电动重载卡车市场需求灰色预测模型

根据已有信息对含有不确定因素的信息进行模糊预测时,可以使用灰色预测方法。将所有移植数据相勾连,通过系统数据的发展趋势进行相关性规律的变动[3]。设置FM(1,1)模型作为数据随机性的非负序列,此时的原始数据列为

式中:Y(0)为所有需要进行预测的原始数据对;n为原始数据列的数据个数。随着随机性数据的增加,预测结果也会逐渐发生变化。此时,可以将增加处理后的原始数据预测结果用公式(2)表示

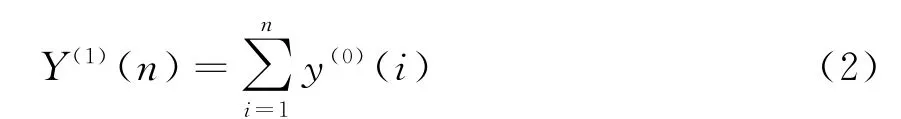
通过公式(2)可以得到一个新的数据队,即Y(1)(n),i为常数。在累加数据的过程中,有一些关联度很弱的相对误差序列,需要在背景值中计算累减的生成序列[45]。此时可以将公式(1)中的原始序列以此展开,并代入最小二乘法进行参数向量的辨识,得到

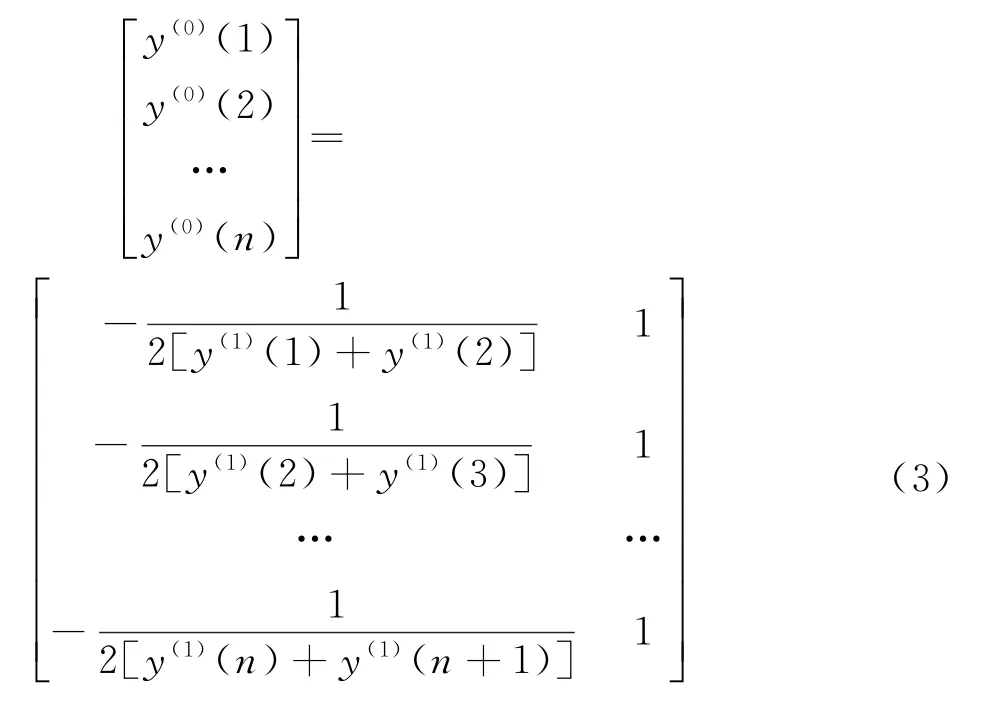
通过公式(3)可以计算关联度的检验误差,在预测值以及原始值的关联中,如果大于0.5,则可以判定其为相对满意的状态。在后验差的检验中,标准差的计算公式为

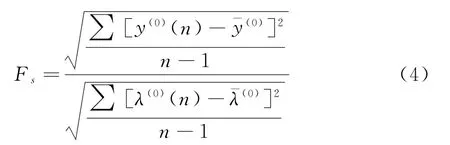
式中:Fs为最小误差概率;λ(0)(n)为绝对误差的相对标准差;为原始序列的标准平均值;为第1序列的相对标准差平均值[6-8]。根据公式(1)—(4)可以得到电动重载卡车市场需求灰色预测模型。

2 基于马尔可夫模型修正误差参数

在马尔科夫模型中,存在多个转移状态,而且每个被转移状态都需要依赖前一个状态,这样就能够得到一个具备模型连贯性的算法模型。由于灰度预测模型在随机发展中的不确定性,需要通过马尔可夫模型对误差参数进行修正,以提高市场需求预测的准确率[9]。在马尔科夫链中,有一个随机数列,被集中于状态空间中。此时的状态空间被过去状态的条件概率集中在同一个函数,等待条件概率的转移。假设此时的随机变量均为一个完整数列,则这些条件概率分布的函数可以表示为

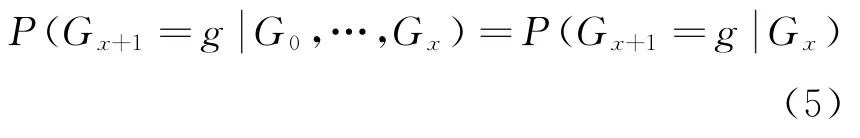
式中:Gx为当前时段内的变量状态;Gx+1为过去状态下的变量分布概率;G0为第1序列的随机变量状态;L为随机变量分布;g为条件概率转移状态。在这样的状态转移过程中,有一个具备N阶不同参数的概率分布条件,可以将五元组表示出2个隐含状态和1个直观状态[10]。此时的隐藏状态中有1个初始时刻的概率矩阵,将这个初始矩阵作为隐藏状态与观察状态的转译概率,可以得到马尔可夫模型的转移拓扑图,见图1。

如图1所示,在转移拓扑模型中,具备5个隐藏状态的转移概率,此时可以通过计算隐藏状态与转移状态的相对矩阵,得到马尔可夫模型的参数修正结果[11]。

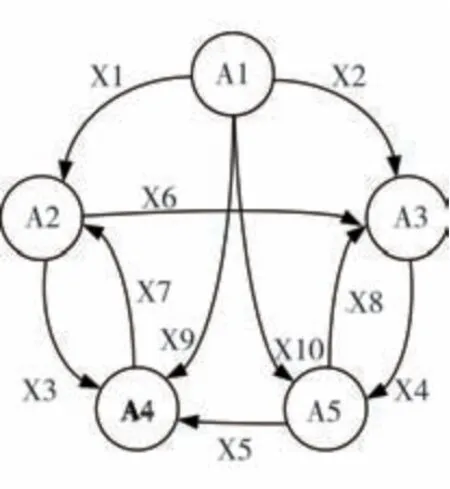
图1 转移拓扑模型

3 市场需求预测算法的构建

通过以上方法获得市场需求预测的参数修正结果后,可以据此设计多个基于马尔可夫模型的电动重载卡车市场需求预测算法,算法流程如图2所示。

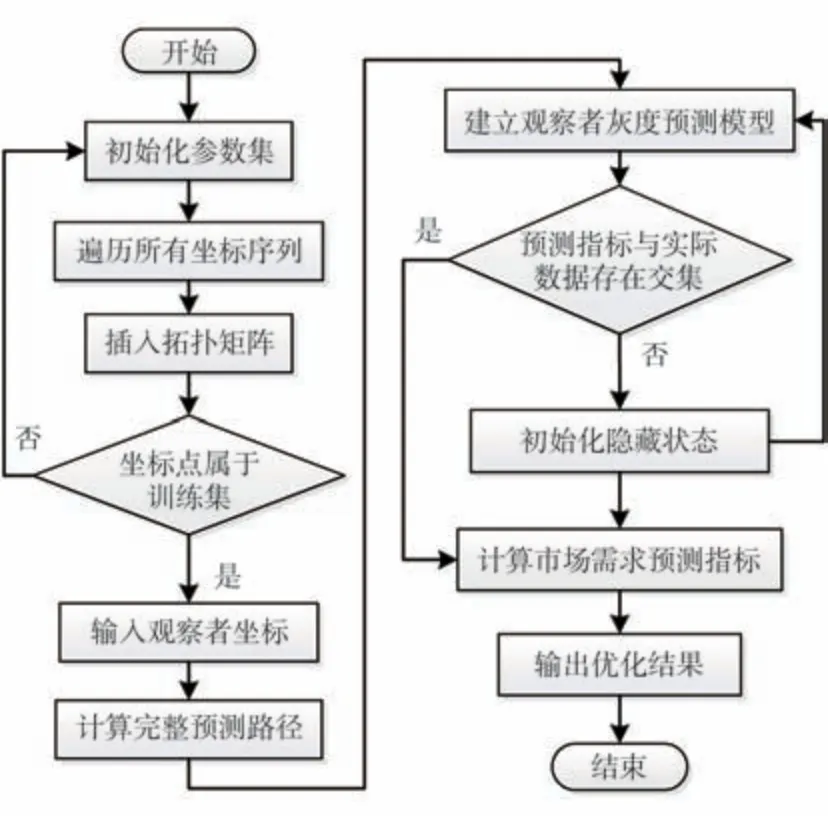
图2 算法流程

如图2所示,在初始化参数集后,需要将所有时间坐标节点全部遍历,将其中的任意序列均插入到拓扑矩阵中。若寻找到不属于训练集的坐标点,则重新初始化参数集。输入所有已知的观察点坐标,并计算市场需求的预测路径。建立观察者的灰度预测模型,以便通过时间推移的方式获取更久远时间段的预测结果[1213]。判定预测指标与实际数据的交集程度,此时若存在交集,则可以直接计算市场需求,并得到预测指标;若不存在交集,则需要初始化隐藏状态,并重新建立灰度预测模型,此时的预测模型可以计算时间段较长的市场需求。

4 市场需求量预测

4.1 确定影响因子及建立预测模型

文中设计了一种基于马尔可夫模型的电动载重卡车市场需求预测方法,为测试该预测方法的准确性,以2014—2017年电动载重卡车的市场销售数据为基础,对2018—2021年的电动载重卡车市场销售额进行预测分析,并与已经统计出结果的数据进行对比,判断该方法的准确性[14]。2014—2017年电动载重卡车的市场销售数据如表1所示。

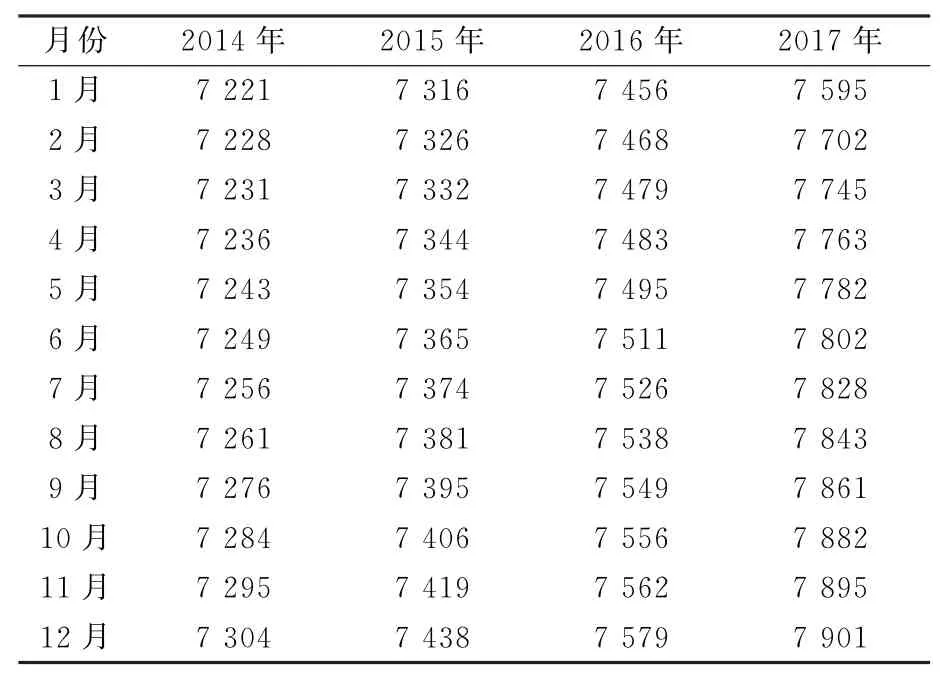
表1 2014—2017年电动载重卡车销售数据 辆

在现有电动载重卡车市场销售量的研究中,对销售额度影响最大的因素主要有货物运输里程、公路运货量、区域人口数量、城市化率、电力消费总量5种因素。设置变量的选择标准,在不同的条件下,设相关系数Pf＜0.01,且不低于0.9。在多元线性回归方程中,可以计算自变量与因变量之间的关系,此时的模型函数为

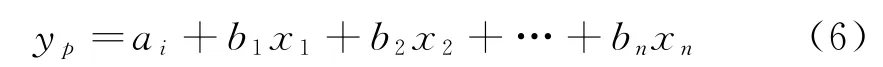
式中:yp为多元线性回归模型的因变量参数值;b1、b2、bn为变量x1、x2、xn的系数,此时n=1、2、3、4、5;ai表示5个影响因素之间的相关性[15]。通过SPSS统计分析方法将5种影响因素对电动载重卡车市场的需求进行相关性验证,可以得到矩阵

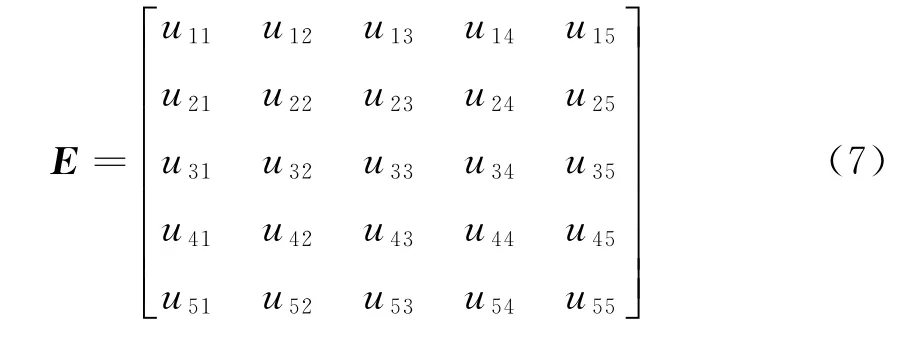
式中:E为5种影响因素对电动载重卡车的市场需求相关性权重指数,i、j=1、2、3、4、5;u11为载重卡车的货物运输里程;u22为单位里程公路的运货量;u33为区域人口数量;u44为城市化率;u55为电动载重卡车的电力消费总量。根据以上因素,建立电动载重卡车的市场需求量组合预测模型[16]。为了提高预测的精准度,使用标准差法计算组合权重,设置指数平滑模型的多元回归标准差分别为σi和σj。此时可以得到2个参数的计算公式

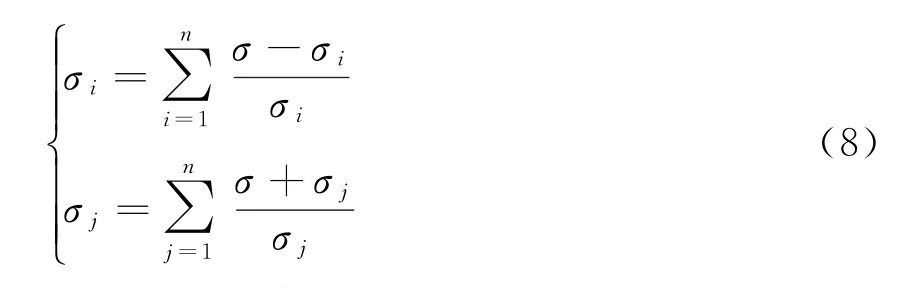
在计算2个参数的模型权重后,可以根据该组合权重,建立预测模型

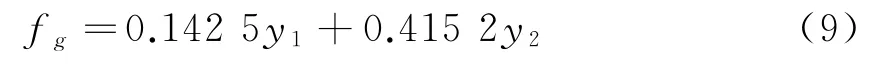
式中:fg为市场需求的预测值;y1为指数平滑预测值;y2为多元回归预测值。根据该预测模型,可以直接预测该产品的市场需求。

4.2 市场需求量预测结果

结合上文中得到的预测模型,对比基于TEI@I方法论的预测模型以及基于RBF神经网络算法的需求预测方法,得到2018—2021年的电动载重卡车市场销售额预测结果。获取2018—2021年电动载重卡车市场的整体销售额,作为该产品的实际需求量数据,用以对比不同方法的预测差异值。2018—2021年电动载重卡车市场的整体销售额如表2所示。

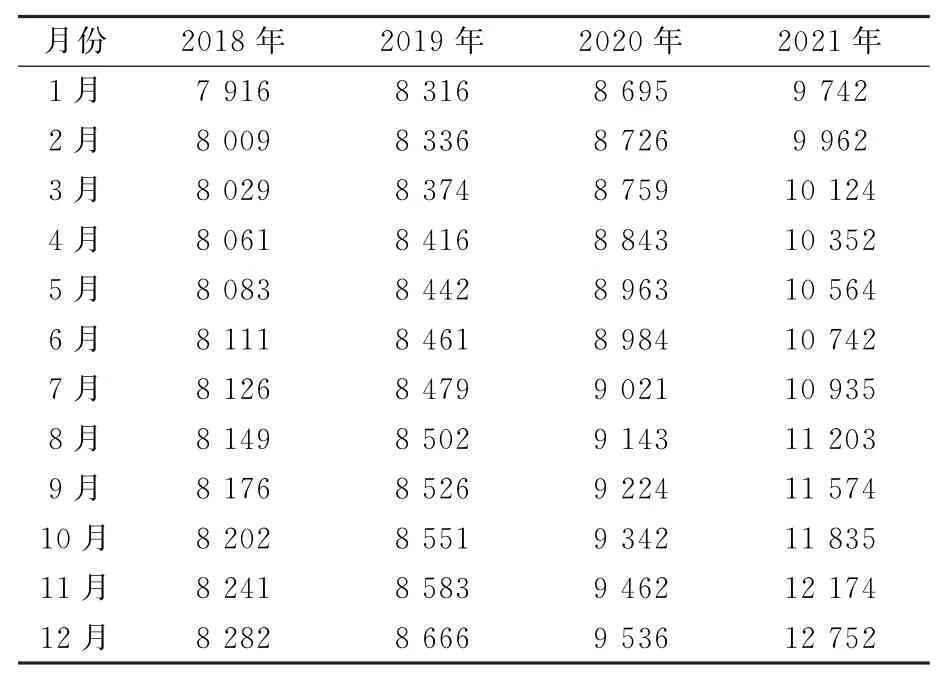
表2 2018—2021年电动载重卡车销售额 辆

得到2018—2021年实际需求量数据后,计算预测结果与实际需求量之间的差异值,计算公式为

式中:λ为预测结果与实际结果之间的差异值;fx为该产品的实际需求量。通过以上公式计算,得到了不同方法的预测差异值,如图3所示。

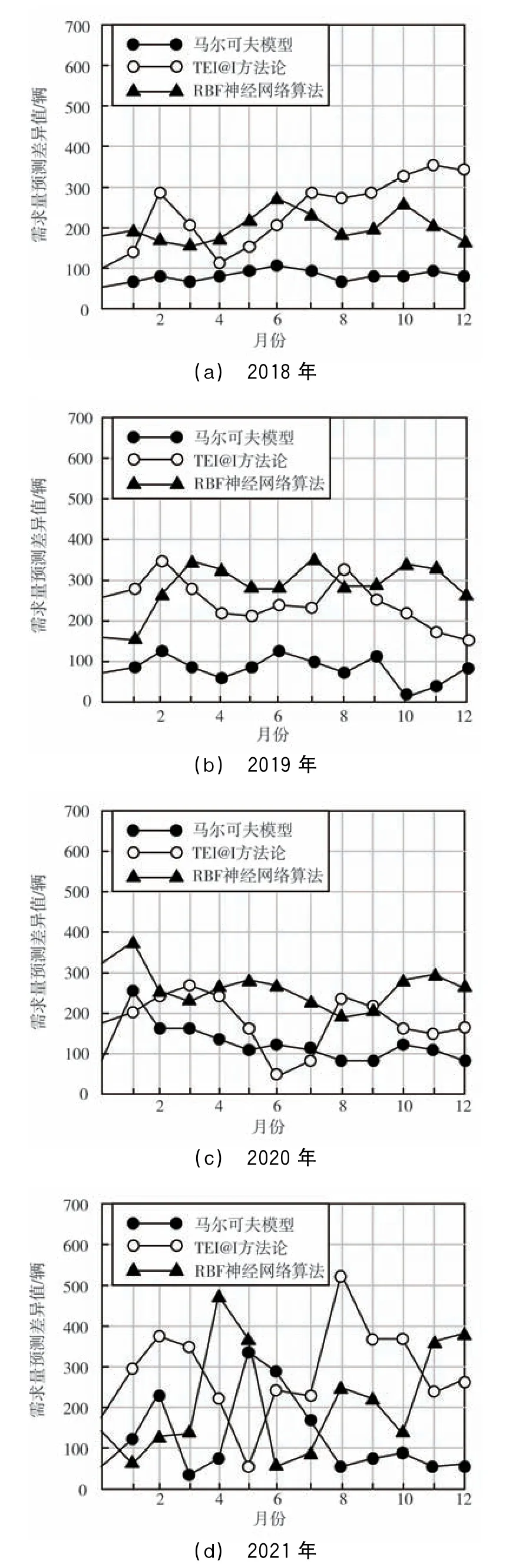
图3 不同方法的预测差异值

如图3所示,自2018年起,随着时间点的后移,3种市场需求预测模型的差异值变化幅度在不断增加,2018年的差异值相对平稳,但是时间越向后,差异值的变化趋势就越明显,且通过马尔可夫模型得到的需求量预测差异值明显小于其他2种方法。为了使结果更加直观,将不同方法的需求量预测差异平均值以表格形式进行展示,如表3所示。

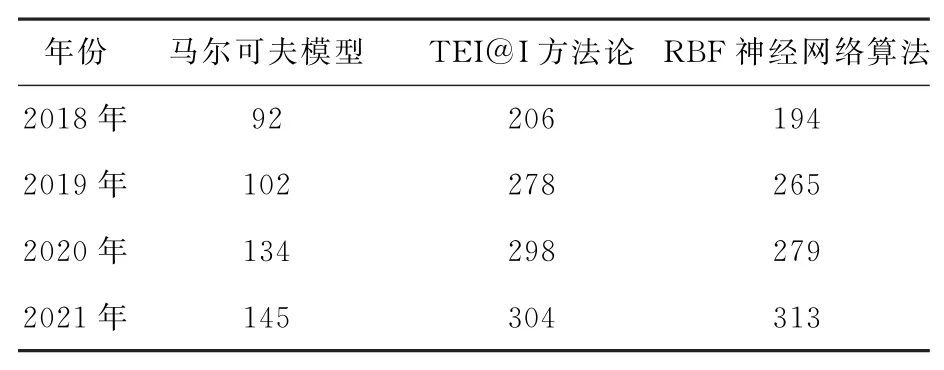
表3 不同方法的需求量预测差异平均值 辆

马尔可夫模型的需求量预测差异平均值最高为145辆,而另2种方法的需求量预测差异平均值均超过300辆以上,由此可以说明本文设计的马尔可夫模型的需求量预测差异平均值较低,对于电动重载卡车市场需求预测的准确度更高。

5 结论

本文基于马尔可夫模型设计了一个电动重载卡车的市场需求预测方法,构建灰色预测模型,使用马尔可夫模型对参数进行优化与改正,实现基于马尔可夫模型的电动重载卡车市场需求预测方法的设计。并通过实验验证了设计方法能够有效对2018-2021年内电动重载卡车的市场需求进行精准预测,预测结果较为稳定。虽然设计方法的预测精度较高,但是由于时间的限制,本文并未分析电动重载卡车市场存在的制约性,因此,在接下来的研究中,将着重分析市场需求预测过程中的影响因素,不断完善设计方法,在预测过程中重点关注影响因素带来的变化,提高预测方法的准确性,以期为电动重载卡车未来的规划与推广提供一定的技术支持。