基于混凝土损伤模型的盾构隧道极限承载力研究

施成华，王祖贤，刘建文，雷明锋, ，彭立敏，彭铸

(1.中南大学 土木工程学院，湖南 长沙，410075；2.中南大学 重载铁路工程结构教育部重点实验室，湖南 长沙，410075)

城市地下轨道交通系统的开发利用是解决现代化都市交通拥挤、土地资源紧张等问题以及建设资源节约型和环境友好型社会的重要途径，国内外普遍采用机械化自动化程度高、施工速度快、安全可靠的盾构隧道技术修建城市地下轨道交通隧道[1-3]。随着城市的发展，近年来在地铁邻近区域进行的工程活动日益增多，由此引发既有盾构隧道围岩应力场发生变化，进而造成盾构隧道出现大变形、接头渗漏水等病害，更有甚者直接导致结构失效[4-5]。作为设计服役寿命达100 a的地下永久性设施，构建行之有效的计算分析方法对不同应力水平下盾构隧道的极限承载力和服役性能的研究具有重要意义。当前，针对该问题的研究可归为3类：解析计算模型、模型试验研究和数值模拟。人们对盾构隧道环向解析力学模型的研究很多，通常基于线路最不利断面结合荷载-结构模式进行隧道横截面的力学计算，此类模型可归为平面应变问题的二维或假三维模型，应用广泛且极具代表性的模型包括匀质圆环模型(惯用法模型)、等效刚度圆环模型(修正惯用法模型)、多铰圆环模型以及梁(壳)-弹簧模型[6-10]。惯用法模型认为盾构隧道管环为匀质圆环，接头刚度与管片刚度保持一致，忽略薄弱的接头结构对整体刚度的影响，因而又被称为完全等刚度环模型。该模型计算简便，但明显高估了整体结构的刚度，导致对得到的变形量估计不足，高估了结构的承载力。在此基础上，考虑接头弱化作用的修正惯用法模型应运而生，该模型认为管环在全圆周上具有相同的弯曲刚度，并引入刚度有效率对结构刚度进行折减，但其主要问题在于刚度的合理取值难以统一[8]。多铰圆环模型则将管片接头模拟为自由铰和弹性铰，该模型的主要缺陷在于：一方面，模型自身为多铰非静定体系，结构稳定依赖围岩约束；另一方面，模型仅适用于地质条件较好的情况，而在软弱围岩条件下其计算结果存在较大偏差，模型适用性受限[9]。梁-弹簧模型采用直梁或曲梁模拟管片单元，采用旋转弹簧和剪切弹簧模拟环内纵向接头和环间接头，因而，环内的抗弯及环间的抗剪效应都能得到有效模拟，且能够计算和评估管片错缝拼装效果，从而将平面问题拓展为假三维问题[10]。在此基础上，研究者又相继提出梁-接头模型[11]、壳-弹簧模型[12]、非均质等效梁模型[1]等，尽管如此，接头刚度的合理取值仍未得到有效解决，大多基于经验或模型试验选取。

基于模型试验开展的研究最为直接，尤以原型试验的结果最可靠。然而，限于试验场地、设备、费用等因素，开展盾构隧道足尺原型试验的研究很少。大部分原型试验以验证设计隧道在特定地层条件和围岩荷载下结构的稳定性和安全性为目的。SCHREYER等[13]对德国Elbe River Tunnel进行了足尺试验以验证结构的承载力和稳定性。NAKAMURA等[14]则对日本Kyoto矩形地铁盾构隧道进行了足尺试验，根据设计荷载作用下结构的力学行为试验结果，验证了结构的安全性，还论证了所采用的设计方法的可靠性。FENG等[15]则以国内大型水下盾构隧道狮子洋隧道为研究对象，基于足尺试验研究了管片接头的压弯力学行为。随着既有线邻近区域工程活动的日益频繁，施工扰动对既有盾构隧道结构的影响不可忽视。LIU等[16]通过制定合适的加载制度模拟隧道周围应力场的变化，对上海典型地铁盾构隧道开展了足尺模型试验，研究了隧道结构的极限承载力、接头力学行为以及结构失效破坏模式。

解析法虽计算简便，但由于其模型参数的合理取值不易确定且模型过于简化，因而在分析复杂问题时应用受限。模型试验则存在耗资、耗时较高等问题，部分试验还对场地、环境及设备有严格要求。相比较而言，基于有限元平台的数值模拟技术是分析复杂问题最常用且高效的手段之一。在针对盾构隧道的数值建模中，其薄弱的接头部位对隧道整体刚度及服役性能影响显著，因此，对接头部位的处理是盾构隧道数值建模的关键所在。最为简便的做法是将盾构隧道简化为等效均质环，并采用刚度折减系数对刚度进行折减[17-19]。该模型虽建模简单、计算高效，但刚度折减系数对计算结果影响较大。另一种则将接头模拟为线性弹簧或者接头单元，仍是一种简化的做法，计算结果对弹簧刚度和接头单元参数的取值敏感，难以真实地反映力学行为[20-21]。近年来，对于盾构隧道的模拟朝着更为精细、复杂的方向发展，基于非线性接触理论发展而来的盾构隧道三维非连续接触模型被普遍采用[22-25]。该模型基于非线性接触理论模拟接头管片与管片之间、衬砌与围岩之间的相互作用关系，最后建立三维精细化盾构隧道拼装模型，在盾构隧道纵、环向力学分析及结构动力响应研究方面具有较强的适应性。

然而，解析模型普遍基于弹性理论求解，数值模拟方法则考虑了围岩、螺栓等材料的塑性变形。可见，既有研究大多是在弹塑性理论框架内进行的，而混凝土材料具有性能劣化、刚度退化等非线性力学特性，采用现代损伤力学理论描述较合适。盾构隧道承受极限承载力时，势必出现结构大变形、裂纹发展等现象，最终导致结构失效破坏。因此，在分析此类结构损伤失效问题时，应突破传统弹塑性理论分析框架，采用损伤力学理论较合理。目前，人们对混凝土管片的损伤劣化行为研究很少。文献[26]基于混凝土损伤模型对卸载作用下盾构隧道的损伤劣化行为进行了研究，构建了一套有效的分析计算方法。但由于结构变形较小，引起结构的损伤以局部损伤为主，结构完整性和安全性程度较高，远未达到失效破坏的程度。为此，本文作者提出一种基于损伤的盾构隧道极限承载力分析方法，以合理地模拟结构的损伤渐进破坏行为。首先，引入一种基于能量的应力分解的双标量弹塑性损伤本构模型以描述混凝土材料的损伤劣化行为；而后，基于三维非连续接触模型构建盾构隧道精细化数值计算模型，通过与文献[16]中足尺模型试验结果进行对比，验证本文分析方法的有效性，进而探讨盾构隧道的极限承载力及损伤特性。

1 混凝土弹塑性损伤本构模型

混凝土作为一种准脆性材料，具有典型的单边效应，受拉时表现为脆性，而受压时表现为塑性，且抗压强度显著高于抗拉强度[27-28]。一般采用双标量损伤本构模型描述混凝土在这种拉、压状态下截然不同的力学特性，其应力-应变关系可表述为

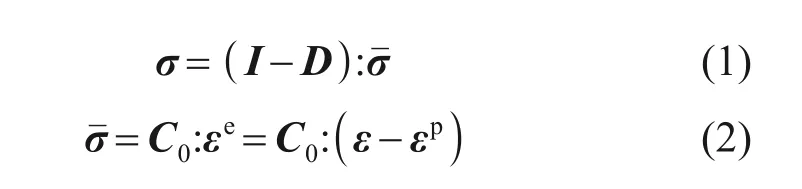
式中：σ为名义应力张量；为有效应力张量，反映混凝土无损部分的应力状态；I，D和C0分别表示4阶单位张量、4阶损伤张量和4阶刚度张量；εe为弹性应变张量，为应变张量ε与塑性应变张量εp之差，εe=ε-εp；:为张量的双并积运算。

由式(1)和(2)可知，在理论塑性模型中，损伤和塑性变形相互耦合，求解时需反复迭代多次，计算效率较低。此处采用经验塑性模型进行求解，其表达式为[29]

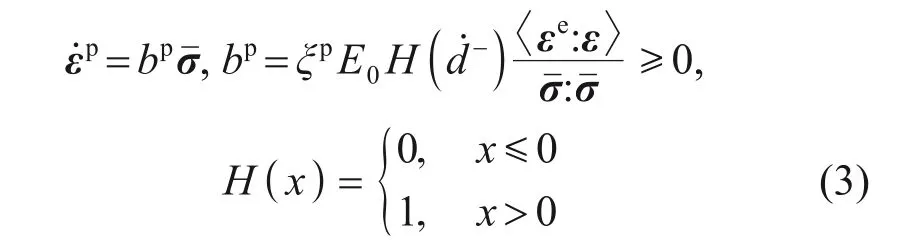
式中：为塑性应变率张量；bp为与塑性应变率相关的系数；ξp为模型参数；E0为混凝土弹性模量；-为压损伤；为McCauley符号，其运算法则为；H(·)为Heaviside函数。

为区分混凝土材料在拉、压应力状态下的力学行为，有效应力张量可表示为正(拉)有效应力张量和负(压)有效应力张量之和：

文献[26,30]指出，经典正/负应力分解策略无法保证刚度张量的主对称性以及在单轴拉时会产生不合理的侧向变形，并非最优的分解策略。而基于能量的分解策略能够克服这一缺陷，单轴受拉时模拟的侧向变形始终处于弹性加/卸载状态，不会产生不合理的侧向变形。基于能量分解策略的正/负应力张量可表示为：

引入拉/压损伤变量d+/d-，混凝土双标量损伤模型的名义应力σ与拉/压有效应力张量的关系可表示为

由此，式(1)中的4阶损伤张量可改写为

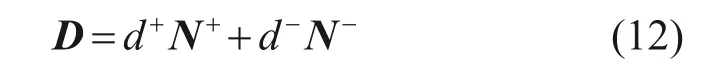
损伤演化法则可参考规范文献[31]给出的单轴条件下混凝土损伤本构模型，损伤由应变驱动。根据损伤一致性条件和能量等效原则，多轴应力状态下单元的等效应变可表示为

在一般应力状态下，混凝土拉/压损伤演化法则可表达为

2 模型的建立

2.1 三维非连续接触模型

文献[16]对上海通用地铁盾构隧道开展了隧道环足尺加载试验，试验结果可为本文数值模型有效性验证提供参考，隧道的结构形式如图2 所示。管环由6块预制钢筋混凝土管片通过高强螺栓拼装而成，分为1 块封顶块F(对应的圆心角为16°)、2块邻接块L1和L2(圆心角为65°)、2块标准块B1和B2(圆心角为65°)以及1块封底块D(圆心角为84°)。隧道外径为6.20 m，壁厚为0.35 m，环宽为1.20 m。每个接头通过2根直螺栓将相邻管片连接，螺杆和螺帽尺寸(直径×长度)分别为30 mm×400 mm 和50 mm×30 mm。

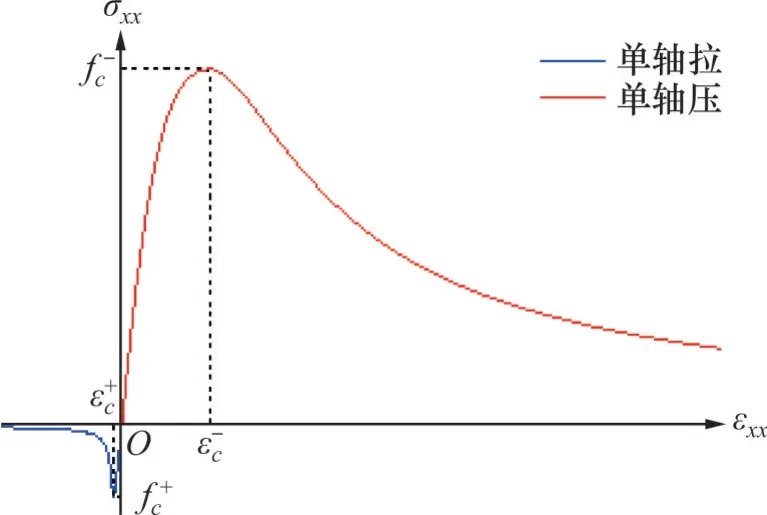
图1 混凝土单轴拉、压应力-应变曲线Fig.1 Stress-strain relationship curve of concrete under uniaxial tension and compression

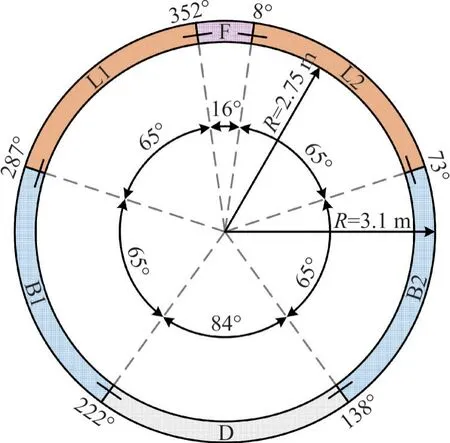
图2 盾构隧道结构型式Fig.2 Geometry of shield tunnel

基于三维非线性接触理论构建精细化三维数值计算模型，文献[22-26]详细研究了该模型，并将其成功应用于盾构隧道纵、环向力学行为分析、结构静动力响应特性以及损伤劣化行为研究。本文基于ABAQUS 有限元平台构建的单环精细化数值模型如图3所示。模型中考虑钢筋的作用，环内侧和外侧环向主筋直径分别为20 mm 和16 mm，内、外侧主筋数量分别为8 根和10 根。钢筋采用梁单元B31模拟，螺栓和管片则采用三维实体单元C3D8R 模拟，钢筋和螺栓均嵌入(embedded)管片实体单元中。接头管片与管片之间相互作用关系采用“面面接触”模拟，接触面法向行为采用“硬接触”模拟，切向行为采用Cloumb摩擦模拟，若接触面闭合，则接触面可传递摩擦力[22-26]。

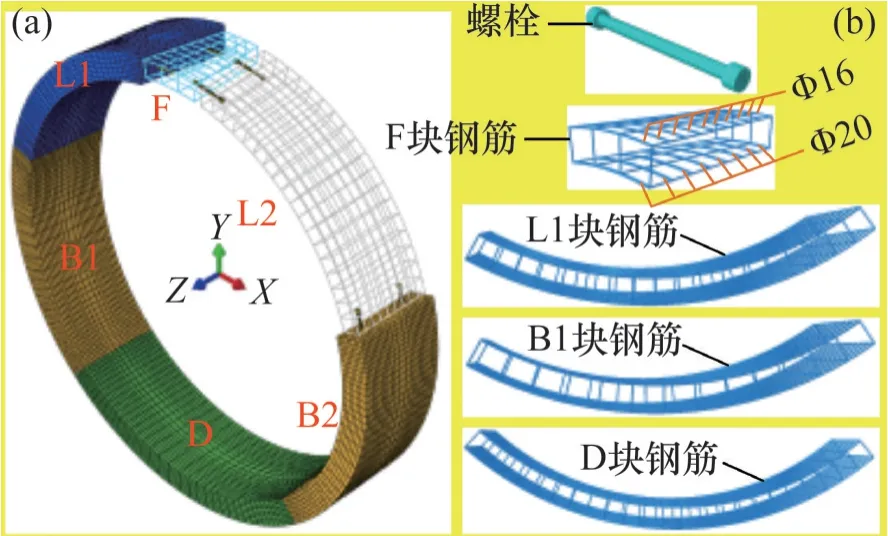
图3 盾构隧道单环精细化数值计算模型Fig.3 Refined numerical calculation model of a segment ring of shield tunnel

2.2 本构模型及材料参数

钢筋和螺栓采用理想弹塑性本构模型模拟，弹性模量和泊松比分别取200 GPa 和0.3，钢筋等级为HRB 335，屈服强度335 MPa；螺栓为5.8 级高强螺栓，屈服强度为400 MPa。管片混凝土等级为C55，采用前述损伤本构模型，模型参数见表1。考虑到计算中涉及结构大变形及单元失效等因素，调用ABAQUS/Explicit求解器能有效克服计算收敛困难等问题，因此，需编制用户材料VUMAT子程序才能采用混凝土损伤本构模型进行数值计算。

表1 管片混凝土相关力学参数Table 1 Related mechanical parameters of segmental concrete

2.3 加载制度

模型中荷载施加位置与文献[16]所述试验保持一致，如图4(a)所示，在24个圆心角间隔15°布置的加载点通过千斤顶施加指向圆心的径向荷载P1，P2和P3。在拱顶和拱底各布置3个加载点施加荷载P1；在两侧拱腰处各布置5 个加载点施加荷载P2；其余加载点则施加荷载P3。试验加载过程如图4(b)所示，分2个阶段加载：第一阶段，P1，P2和P3均从0 kN 开始线性增加，P2加载至275 kN，P1=1.54×P2，P3=0.5×(P1+P2)；第二阶段，P2保持不变，P1保持线性增加直至达到极限荷载(结构破坏)，P3亦呈线性增加且在整个加载过程中保持P3=0.5×(P1+P2)。

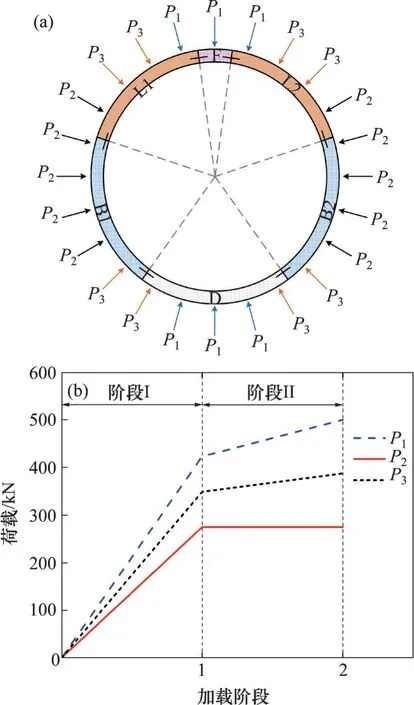
图4 加载方案Fig.4 Loading scheme

3 计算结果分析

3.1 结构变形

图5 所示为数值模拟结果与试验结果的对比。由图5(a)中的原始试验结果可见，在试验过程中，结构刚度(荷载-收敛变形曲线的斜率)在加载初期较小而后增大。但对理想无损结构而言，其刚度应在加载初期最大，之后，随着材料屈服，损伤的发展而逐渐衰减。造成这种现象的原因可能是试验模型管片拼装、加载设备与模型之间、量测设备与模型之间存在间隙，初期加载使得间隙闭合，由此造成该阶段出现较大位移，而数值模拟较难反映此类间隙的影响。为此，需要对试验原始值曲线进行适当调整，将合理刚度阶段曲线延拓，以消除初始间隙的影响。

图5(a)所示为加载过程中的荷载-收敛变形曲线(P1-x曲线)，图5(b)所示为加载过程中荷载增量-收敛变形增量演化即结构刚度演化曲线(ΔP1-Δx曲线)。由图5可知：本文基于损伤模拟得到的P1-x曲线与调整后的试验曲线接近。可以发现单环隧道加载失效破坏可近似划分为3个阶段。

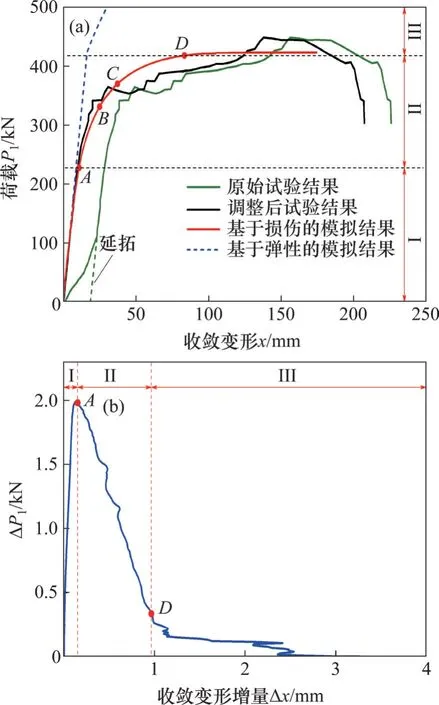
图5 数值模拟结果与试验结果的对比Fig.5 Comparison of the results obtained by numerical simulation and experiment

1) 阶段I：线弹性阶段，对应于P1-x曲线和ΔP1-Δx曲线的OA段，对应的荷载范围为0≤P1≤227.62 kN，位移范围为0≤x≤10.67 mm(0≤x≤0.17%Dt，Dt为隧道直径)。该阶段结构整体保持线弹性状态，刚度较大。

2) 阶段II：损伤-屈服阶段，对应于P1-x曲线和ΔP1-Δx曲线的AD段，对应的荷载范围为227.62≤P1≤418.12 kN，位移范围为0.17%Dt≤x≤1.34%Dt。该阶段结构刚度逐渐衰减，管片萌生裂纹、发展、连通，部分接头螺栓和钢筋逐渐进入屈服阶段。

3) 阶段III：失效破坏阶段，对应的荷载范围为P1≥418.12 kN，位移范围为x≥1.34%Dt。该阶段结构刚度逐渐衰减至0，管片出现大面积损伤，多条裂纹贯通，螺栓大部分屈服，结构出现多个塑性铰，最终失效破坏。

根据以上分析，结构的极限承载力可定义为P1-x曲线上D点对应的荷载，即本文模拟得到的单环盾构隧道的极限承载力为418.12 kN，而试验得到的极限承载力为448.00 kN，相差约6.67%。一般而言，正常服役状态下的盾构隧道不太可能出现如此显著的收敛变形，在日常检测中也容易发现和规避。此外，我国地铁相关规范[32]明确规定盾构隧道最大收敛变形应控制在0.4%Dt～0.6%Dt以内，分别对应于图5(a)中P1-x曲线上的B点和C点对应的收敛变形，相应的荷载分别为331.19 kN和370.26 kN，此时，结构性能约处于阶段II 的中后期。由此，本文定义盾构隧道结构的正常服役性能极限承载力为最大收敛变形达到规范规定的限值0.6%Dt时对应的荷载，此时，结构处于损伤-屈服阶段中后期，尚留有约11.45%富余承载力。另一方面，通过对比基于弹性本构的模拟结果可以发现，P1-x曲线呈线性增加，对其破坏失效的过程亦不能得到有效模拟，明显高估了结构刚度和承载能力。可见，传统方法将混凝土管片模拟为弹性体存在局限性。

3.2 管片裂损特性

图6和图7所示为加载过程中管片损伤发展云图。由图6 和图7 可知：由于混凝土抗拉强度较低，管环受荷载作用时结构出现明显的拉损伤(裂纹)；随着荷载逐渐增大，在拱顶、拱底内缘最先出现裂纹，接缝螺栓连接处由于螺栓拉应力的作用亦出现较明显的局部损伤。

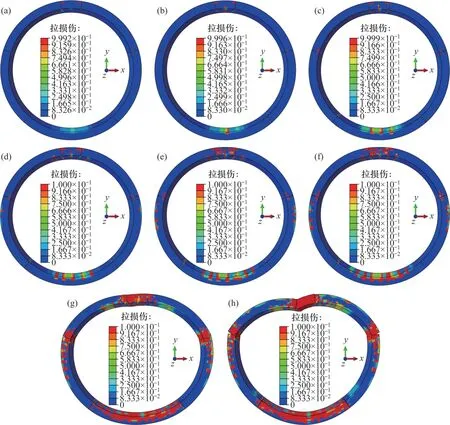
图6 混凝土管片拉损伤演化规律Fig.6 Tensile damage evolution of concrete segment

当加载至线弹性阶段末段时(A点荷载状态，如图6(b)所示)，拱顶和拱底内缘已出现浅层裂纹，结构由线弹性状态逐渐过渡至屈服-损伤阶段。继续加载时，拱顶和拱底裂纹数量、裂纹深度均逐渐增大，在P1达到270 kN 左右时(如图6(d)所示)，在拱腰外缘开始出现裂纹，拱顶则新发展2 条裂纹；而后，拱顶、拱底和两侧拱腰处裂纹数量、深度随着荷载增加继续增大；当达到盾构隧道正常服役性能极限承载力时(C点荷载状态，如图6(f)所示)，拱底内缘和两侧拱腰外缘出现数条裂纹，拱顶管片出现大面积损伤，部分裂纹呈现相互连通之势。进入损伤-屈服阶段末期时(D点荷载状态，如图6(g)所示)，拱底内缘出现大面积损伤区域，两侧拱腰外缘裂纹数量进一步增加，拱腰处接头(73°和287°)和拱顶接头(8°和352°)损伤严重，接头塑性铰初步形成。加载至结构失效破坏时，整环结构最终在拱顶和拱腰接头处形成4 个塑性铰。

此外，由图7可见：在整个加载过程中，结构的压损伤并不显著，在结构失效阶段(如图7(c)和图7(d)所示)，拱顶外缘和拱腰接头内缘由于应力集中出现较明显的压损伤，混凝土管片表现为接缝位置局部压溃，352°接头外表层混凝土受剪剥落。

图8 为试验中的管片裂损情况，由图8 可见：在拱顶接头(352°接头)外缘以及拱腰接头(73°接头和287°接头)内缘有明显的混凝土压溃剥落，与数值模拟的受压损伤云图较吻合(见图7(c)和(d))；拱腰接头内缘存在纵向贯穿的拉裂纹(见图8(b)和图8(c))。本文基于损伤的模拟结果(损伤云图6(h))也反映了此试验现象。由图8(d)可知：除接头部位外，受拉裂纹主要分布于拱顶、拱底内缘以及两侧拱腰外缘，拱腰以大量微裂纹为主，而拱底则出现数条连通的宏观裂纹。本文基于损伤的数值模拟得到的受拉损伤云图与足尺试验结果中的受拉裂纹分布较类似，能够在一定程度上反映结构裂纹的分布规律与演化特性。

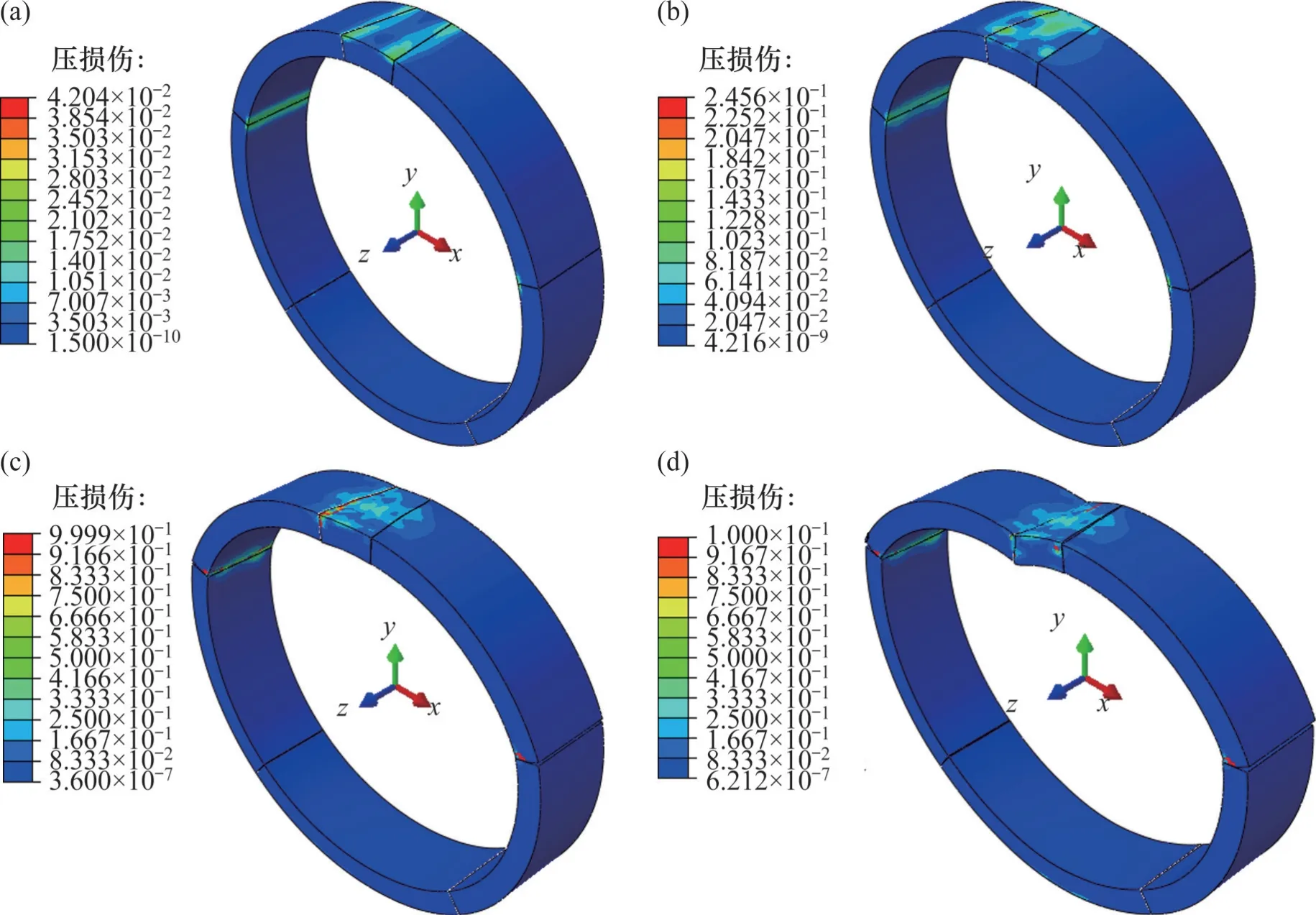
图7 混凝土管片压损伤演化规律Fig.7 Compressive damage evolution of concrete segment

图8 试验中管片裂损情况Fig.8 Segment cracking in the experiment

3.3 结构内力及应力

图9所示为本文模拟得到的单环盾构隧道的轴力和弯矩分布图，轴力以截面受压为负，0°和180°分别对应拱顶和拱底位置，90°和270°则分别对应两侧拱腰位置。由图9可知：在结构破坏之前(图5(a)中D点对应荷载(418.12 kN)之前)，管环各部位轴力随着施加外荷载的增加而呈非线性增加；结构破坏后，由于在拱顶和拱腰位置已形成塑性铰，这2 个部位轴力在阶段III 呈现快速下降趋势，应力重分布后，尚未达到破坏的拱底转而承担转移而来的荷载，由此，拱底轴力出现非线性快速增加的态势。从图9(a)可明显观察到P1=420 kN 时的轴力分布曲线在两侧拱腰和拱顶位置明显穿插至其余曲线之中，轴力衰减明显，而在拱底位置则与其他曲线保持较一致变化规律，逐渐向圈内收缩，轴力增加。从图9(a)可以明显观察到在6处接头位置处轴力显著增加，每处接头影响范围对应的圆心角在6°左右。产生该现象的原因可能是接头部位应力集中，接缝处管片与管片面面接触之间过高的法向应力最终积分为轴力，表现为接头部位轴力曲线出现突变现象。

在图9(c)和图9(d)所示的管环弯矩分布图中，在拱顶左右45°区域和拱底左右50°区域出现内侧受拉，其余部位出现隧道外侧受拉。由图9(c)可见：当P1小于图5(a)中D点对应荷载(418.12 kN)时，衬砌弯矩分布曲线在两侧拱腰处向外膨胀，而在拱顶位置向内收缩；但P1为420 kN 时的管环弯矩分布曲线则与此规律相反。结合图9(d)可知，在结构破坏之前，管环各部位承受的弯矩随着外荷载的增加而增加，但在结构破坏后，拱顶和拱腰部位承受的弯矩显著下降。

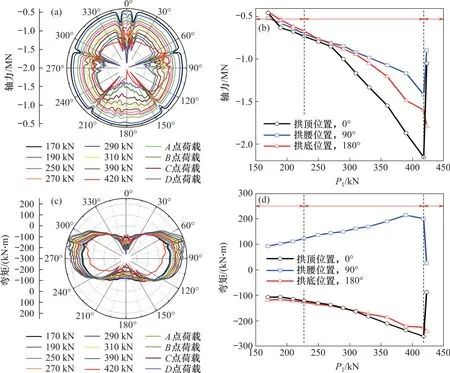
图9 管环结构轴力和弯矩Fig.9 Axial force and bending moment of segment ring

由此可见，结构损伤的发展导致其所承担的内力发生明显改变。需注意的是，结构失效后，衬砌管环实际处于卸载状态，所承担的内力快速衰减。用传统弹塑性模型进行分析时，由于没有考虑材料的损伤劣化特性，因而无法模拟结构内力的衰减过程，而本文基于混凝土损伤的数值模拟结果能够较好地反映该过程。

结构的损伤分析与传统弹塑性分析的显著区别在于因损伤发展而导致的单元应力重分布现象，因此，需研究结构应力分布的演化与损伤发展之间的关系。

图10 所示为拱底封底块D 管片钢筋的应力云图。由图10 可知：封底块钢筋内侧主筋承受拉应力而外侧主筋承受压应力，拉、压应力随着荷载的增加而增加。通过与管片损伤云图(图6)对比可知，管片裂损的部位与钢筋最大拉应力出现的位置一致。在混凝土裂损之前(见图10(a))，钢筋应力连续分布；当P1=190 kN时，封底块出现第一条裂纹，从图10(b)也可观察到管片损伤开裂引起的应力重分布导致内侧主筋中心部位出现明显的局部拉应力集中，但应力较小，约为43.74 MPa，远低于屈服强度335 MPa；随着荷载的增加，封底块出现的裂纹数量逐渐增多，内侧主筋出现应力集中的区域也相应扩大；当达到结构正常服役性能极限状态时(图10(f))，内侧主筋已出现多条应力集中带，最大拉应力达202.8 MPa；在管片大面积损伤时，钢筋应力集中带逐渐连接成片，出现大范围的拉应力集中现象，最大拉应力可达329.6 MPa，已接近钢筋屈服强度。

图10 封底块D钢筋应力云图Fig.10 Stress nephograms of reinforcement in block D

图11所示为拱腰处标准块B1管片钢筋的应力云图。从图11 可见：拱腰处管片钢筋的应力随荷载增加的发展规律与封底块的较类似，外侧主筋承受拉应力，而内侧则承受压应力，在结构失效之前，最大拉、压应力随着荷载增加而增加，最大拉应力达186.1 MPa 左右，低于钢筋屈服强度；在管片出现第一条裂纹之前(P1≤270 kN)，钢筋应力分布连续；在管片出现第一条裂纹时，应力重分布导致外侧主筋出现明显的局部应力集中带；而后，随着裂纹数量增加，应力集中带的区域也逐渐增加；当荷载达到极限承载力时(图11(e))，外侧主筋已出现数条大面积应力集中带，而后结构失效破坏，B1 块承受的弯矩和轴力衰减(图9(b)和(d))，相应地，钢筋应力较低。

图11 标准块B1钢筋应力云图Fig.11 Stress nephogram of reinforcement in block B1

图12 所示为混凝土管片最大主应力云图。分析图12与隧道损伤云图(图6)可知：在裂纹出现之前(见图12(a))，管片最大主应力分布较为连续，拱顶、拱底内缘和拱腰外缘承受较大的主拉应力；而当拱底和拱顶出现裂纹时(见图12(b))，可观察到明显的应力重分布现象，在裂纹区域材料失效，因而单元应力降低(红色区域消失)，可在封底块和封顶块看到明显的应力不连续分布现象；继续加载至250 kN，拱底损伤区域增加，最大主应力区域面积逐渐减少，该部分单元力学性能已进入劣化下降阶段，拱腰外缘和拱顶邻接块内缘红色区域面积逐渐扩大且分布连续，此时，拱腰处裂纹尚未发展；当加载至270 kN 时(见图12(e))，拱腰两侧出现第一条裂纹，应力分布不连续，同时拱顶新增2条裂纹，红色应力集中区消失；当加载至结构正常服役性能极限状态时(见图12(f))，拱顶、拱底和两侧拱腰因出现数条裂纹而导致结构最大主应力区域面积进一步减小，应力逐渐向未损伤区域逐渐转移；当结构失效破坏时，管片已出现大面积损伤，结构处于卸载状态，最大主应力区域面积很小。

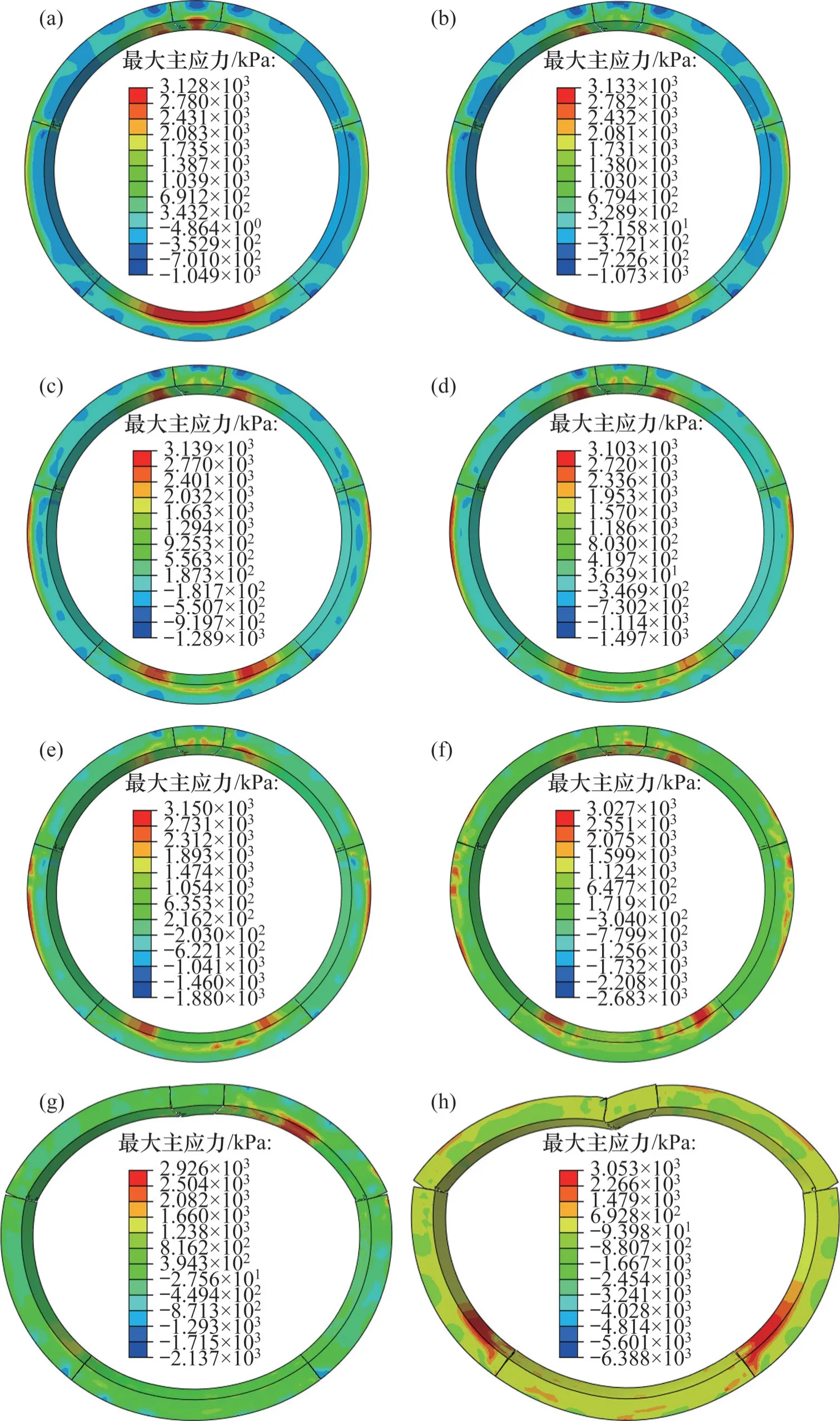
图12 混凝土管片最大主应力云图Fig.12 Nephograms of the maximum principal stress of concrete segment

图13所示为接头螺栓应力与荷载之间的关系。由图13 可知：由于管片开裂导致结构具有非线性刚度，接头螺栓的应力随着荷载增加而呈非线性增加；在P1为370 kN 左右时，拱顶352°接头螺栓率先屈服，稍后，右侧8°处螺栓在P1为378.54 kN时屈服，LIU等[16]由试验得到的该处螺栓屈服时的P1为352 kN；当P1达到411.71 kN左右时，拱腰两侧接头螺栓开始进入屈服状态，试验中对应的P1为392 kN；拱底138°和222°两处接头螺栓在结构失效时仍处于弹性状态，最大应力分别为271 MPa和260 MPa 左右。由此可见，在该试验加载条件下，拱顶接头部位最薄弱，拱腰处接头较易屈服，而拱底处接头偏于安全。值得注意的是，C点荷载(结构正常服役性能极限状态)和D点荷载(结构极限承载状态)与接头螺栓屈服时对应的荷载较吻合。当达到D点荷载时，拱顶和拱腰4处接头螺栓已全部屈服，结构失效破坏。

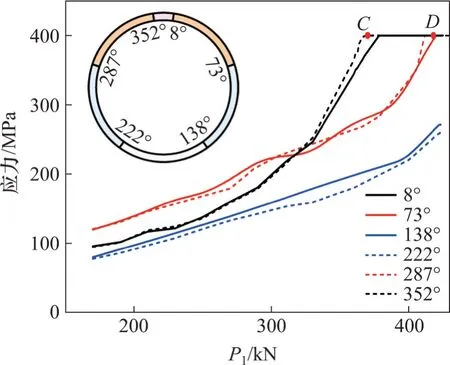
图13 螺栓应力与荷载之间的关系Fig.13 Relationship between bolt stress varied and load

3.4 讨论

通过与试验结果对比，本文基于混凝土损伤本构模型对单环盾构隧道加载直至失效破坏过程的模拟方法的可靠性和合理性得到了验证，加载过程中结构的变形、内力的传递、损伤演化过程、失效模式以及应力重分布等均得到有效反映。管环结构的失效破坏模式表现为拱顶和拱腰附近接头部位出现4 个塑性铰，模拟的极限承载力约为418.12 kN，对应的收敛变形为1.34%Dt，大幅度超过规范允许值。该量值的收敛变形在盾构隧道中较大，在实际工程中不太容易发生，需重点研究具有现实意义的、能客观反映结构服役性能状态的变形指标。

在试验加载机制中，隧道结构的正常服役性能极限承载力的模拟值和试验值分别为370.26 kN和364.74 kN，两者十分接近，此时，管环在拱顶、拱底和两侧拱腰出现多条纵向离散裂纹，但尚未互相连通形成大面积损伤，继续加载时，开始出现成片大面积损伤。此外，当数值模拟的荷载达到370 kN 左右(试验荷载为352 kN)时，拱顶封顶块接头螺栓呈屈服状态，接头塑性铰已具雏形。由此可见，将隧道最大收敛变形限定在0.6%Dt有一定的合理性，可以较合理地反映结构的服役状态，对应的正常服役性能极限承载力为350～370 kN。

4 结论

1) 通过与足尺试验结果对比，本文方法得到的荷载-收敛变形结果与试验结果较吻合，模拟得到的结构损伤开裂结果与试验结果较一致。本文得到的极限承载力为418.12 kN，试验值为448.00 kN，相对误差仅为6.67%。随着加载过程中单元损伤的发展，结构内力的变化以及应力重分布现象也能得到有效模拟。可见，本文基于混凝土损伤本构模型对单环盾构隧道加载直至失效破坏过程的模拟方法具有可靠性和合理性。

2) 隧道结构的失效破坏过程可分为3 个阶段，即线弹性阶段、屈服-损伤阶段和失效破坏阶段。在试验加载制度下，模拟的阶段I和II的荷载限值分别为227.62 kN和418.12 kN，收敛变形限值分别为0.17%Dt和1.34%Dt。

3) 当隧道收敛变形达到规范规定限值0.6%Dt时，对应的隧道结构的正常服役性能极限承载力模拟值为370.26 kN，此时，拱顶、拱底和两侧拱腰出现多条纵向离散裂纹，拱顶接头螺栓进入屈服状态，接头塑性铰已具雏形。可见，将隧道最大收敛变形限定在0.6%Dt有一定的合理性，可以较合理地反映结构的服役状态。

4) 拱顶接头部位最薄弱，拱腰处接头部位次之，而拱底处接头偏于安全。盾构隧道结构的失效模式表现为拱顶和拱腰接头螺栓屈服、混凝土开裂最终形成接头塑性铰而被破坏。