耦合磁滞的电-机械转换器多场建模及参数优化

陈淑梅 ，柯旭锟 ，吴荣钰 ，黄惠，杜恒，李雨铮

(1.福州大学 机械工程及自动化学院，福建 福州，350108；2.流体动力与电液智能控制福建省高校重点实验室，福建 福州，350108)

我国的高端液压元件制造在智能装备制造领域处于“卡脖子”的现状，尤其是高速开关阀的性能亟待提升[1-2]。电-机械转换器作为高速开关阀的核心部件，是阀芯产生高频开关的关键驱动元件，它的响应速度决定了高速开关阀的性能[3]。电磁式的高速开关阀涉及电磁激励、机械开关和液力影响的非线性耦合变量关系，在对整阀进行结构参数设计时，各个物理参数之间的相互作用不可忽略，通过建立电-机械转换器模型来研究其动态特性的方法，对高速开关阀的设计与制造具有重要意义。

BANGURA[4]提出一种用于电机驱动系统设计的电磁场-电路耦合模型，该模型包括直接与状态空间模型耦合的电机二维磁场的有限元模型，采用了一种先进的闭环控制结构，即传统的转矩(或电流)矢量控制，应用于三相绕场无刷起动发电机样机的设计与分析。邱家俊等[5-7]对电机的机电耦联和磁固耦合开展了大量研究。自21 世纪以来，许多学者对电磁高速开关阀物理模型的建立进行了重点研究。针对电磁耦合问题，张胜昌等[8]在研究柴油喷射器用电磁高速开关阀时提出了一种电-磁-机-液耦合方法，建立了非线性的耦合微分方程组，并进一步考虑了磁饱和、涡流等问题；ANGADI 等[9]建立了电磁阀的多物理综合理论模型，考虑了电磁、热力学和固体力学的耦合效应，能够对由于元件热膨胀引起的电磁阀内部应力、应变进行预测，从而降低了线圈短路、电阻降低等故障率。蔡胜年等[10]实现了对电路-磁路-机械-液压之间的物理场耦合建模，并对电磁力、开关响应、流量特性等进行了实验研究并验证了模型的准确性，可为相关控制阀的系统设计提供了参考。

随着近几年对电磁阀多物理场耦合模型的研究不断深入，研究者针对不同结构的电磁阀提出了更加精准的物理模型。FANG等[11]研究了一种高速开关阀执行机构的多物理场模型，将模型分解为机械、电磁子模型，分别建立了弹簧/质量/阻尼系统、非线性电阻/电感系统；TAN 等[12]提出了一种基于有限体积混合激励线性执行器动态特性的优化设计方法，并建立了损耗模型、电磁模型和力学模型，利用三维有限元法进行了优化设计计算。根据试验结果，涡流损耗占总损耗的44.9%，涡流使响应时间增加了8.6%以上，验证了耦合模型的必要性。

学者们对电-机械转换器研究逐渐深入，建立了电、磁、机械等子模型，能较好地描述高速开关阀的运动状态，但是，并没有考虑各个子模型包括各物理量的耦合关系在多物理场模型中的实现，且没有考虑磁滞对高速开关阀的电磁力及频响的影响。因此，本文提出利用COMSOL Multiphysics 建立电-机械转换器的电-磁-固多物理场耦合仿真模型，同时引入J-A磁滞模型拟合磁性材料的磁滞特性，完成电-机械转换器动态仿真模型的建立；搭建了电-机械转换器电磁力测试试验台，验证模型的准确性；最后，运用该模型对电气参数(线圈匝数、激励电压)和结构参数(工作气隙、衔铁长度、弹簧刚度)进行仿真分析，研究各参数对频响的影响，进一步提出缩短转换器频响的措施，为电-机械转换器的优化设计提供依据。

1 结构及原理

1.1 微小型电-机械转换器结构

本文的研究对象是一种典型的弹簧复位式-螺线管型高速开关阀的电-机械转换器，其结构主要由线圈、动衔铁、磁轭、复位弹簧等组成，如图1所示，图中，Fm为电磁力，Fp为弹簧预紧力。高速开关阀的阀芯位移取决于铁芯和衔铁之间的工作气隙，且由限位挡板锁定。

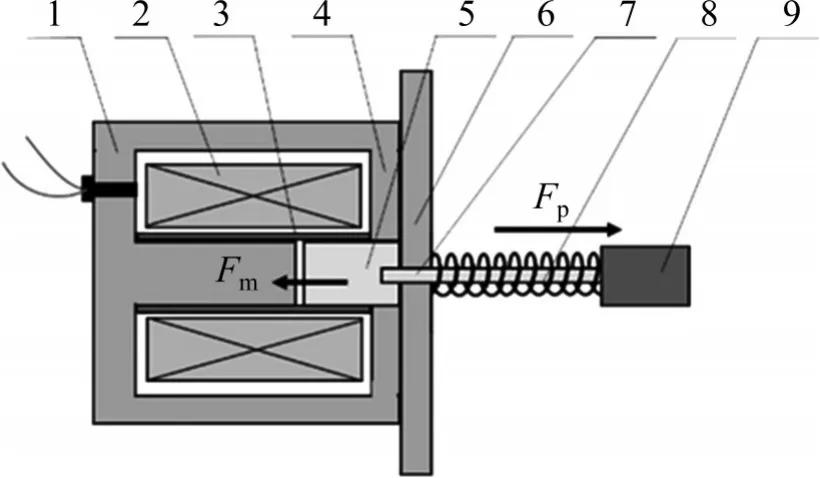
图1 电-机械转换器结构示意图Fig.1 Structure of electro-mechanical converter

1.2 工作原理

电-机械转换器动态过程由外部电压激励、电-磁能量转换和磁能释放产生机械动作3 个部分组成，如图2 所示，图中，R为线圈电阻；L为线圈电感；N为线圈匝数，V为电源电压；Fsp为弹簧力；Ff为摩檫力；m为衔铁质量。外部电压通过驱动电路对线圈进行激励，线圈中的电流产生磁场；衔铁在磁感应强度的作用下产生电磁吸力，电磁吸力克服阻力带动阀芯产生运动；电压切断后，电磁力下降，在弹簧预紧力的作用下，衔铁带动阀芯反向运动。

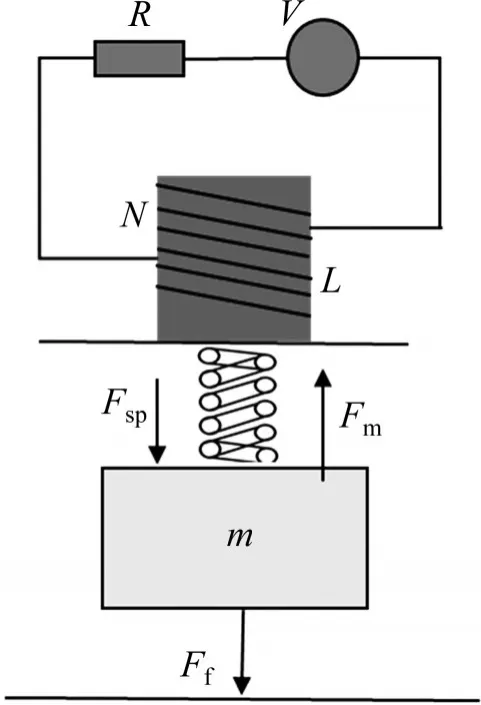
图2 电-机械转换器工作原理图Fig.2 Schematic diagram of electro-mechanical converter

2 多物理场耦合模型建立

2.1 耦合关系

电-机械转换器由激励到运动的过程是从电能到磁能再到机械能的转化过程。电-机械转换器的耦合作用如图3 所示，图中，U为激励电压；i为线圈电流；ϕ为单匝电流产生的磁通量；t为加载时间。在电能转化成磁能的过程中，励磁线圈中电流的变化将导致磁回路中的磁通量发生变化；衔铁运动后，磁路磁阻发生变化，引起线圈电感改变，即励磁线圈中会产生反向的感应电势，对原有电路电流的上升产生阻碍。在磁能转化到机械能的过程中，衔铁在电磁吸力的作用下发生运动，工作气隙随之改变，从而使得总磁路磁阻(包括气隙磁阻和铁芯磁阻)变化，导致总磁通发生变化，电磁吸力产生改变，最终影响电-机械转换器的运动状态。

图3 电-机械转换器的耦合关系示意图Fig.3 Schematic diagram of coupling relationship of electro-mechanical converter

2.1.1 电路激励子环节

电路激励环节是将外部电压加载到线圈，产生驱动电流进而生成磁场的过程。驱动电流的上升时间会影响电磁力的增大，从而影响了电-机械转换器的响应时间。考虑电感受磁路磁阻变化的影响，可得电-机械转换器的电压激励方程、磁阻、电感关系式如下：

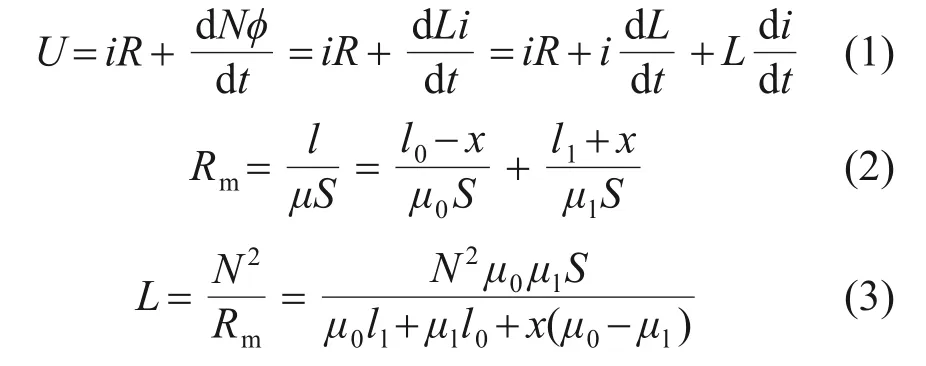
式中：Rm为总磁阻；l为总磁路长度；l0为初始气隙长度；l1为铁芯磁路长度；μ0为真空磁导率；μr为软磁材料的平均磁导率。

2.1.2 磁路转换子环节

电-机械转换器的响应速度主要取决于电磁力，磁路环节在其中发挥着重要的转化作用。它实现了电-机械转换器从电激励到转换成磁能，并在磁路中产生电磁力使得衔铁运动的转化过程。选用麦克斯韦应力张量法的电磁力公式如下：

“我们不是朋友，是敌人。呦呦姐脾气是不好，但是个好人，这样一个人，怎么会有敌人？就像我一样，我没敌人，要说有的话，也只有胡人。”

式中：n为S面的法向量；F为作用于S面内电荷上的库仑力；T为应力张量元；r为所选取计算空间的半球面半径。

2.1.3 机械运动子环节

电-机械转换器的响应速度是影响高速开关阀的重要因素，其高频响应性体现在衔铁开启和关闭的响应过程中。不通油(干式)的电-机械转换器在开启过程中除了受到电磁力外，还需要克服弹簧预紧力和机械摩擦阻力，可以得到运动件在开启和关闭时的动力学方程如下:

式中：k(x0+x)和k(x0+0.6-x)分别为开启和关闭弹簧力；k为弹簧刚度；D=为阻尼系数；x为衔铁位移；为运动件的加速度；Ft为剩余电磁力。

2.2 基于COMSOL的磁滞动态建模

根据转换器的结构及主要参数(如表1 所示)，在COMSOL 中建立电-机械转换器的二维轴对称模型。在材料参数设置方面，上磁轭、下磁轭、衔铁的磁性参数都设置为电工纯铁DT4 的磁性参数。线圈设置为铜材料，导向套和螺纹杆部件均为不导磁材料设置成不锈钢材料，线圈框骨架设置成橡胶材料。利用COMSOL 自带网格划分的功能模块，将电-机械转换器结构分成运动部分的网格和静止结构的固定网格。调用四边形映射网格来划分运动的工作区域，利用三角形自由网格划分其余静止部分的结构以及空气域。调用网格大小设置将运动部分的网格进行细化，使计算的结果更精确。所建立的二维轴对称模型及其网格划分如图4所示。

图4 二维轴对称模型及网格划分Fig.4 Two-dimensional axisymmetric model and meshing

表1 转换器的关键参数Table 1 Key parameters of converter

图5 所示为COMSOL 中电-磁-固耦合模型的实现方案。该模型应用了AC/DC 模块的电磁场接口以及数学模块的全局常微分方程、系数形式偏微分方程和事件接口来模拟转换器动态过程的多物理场耦合模型，其中，电路部分应用式(1)～(3)，机械运动部分应用式(5)和式(6)。将各部分建立耦合关系。最后，通过动态求解器求解亚毫秒级电-机械转换器的运动过程，直接计算电-机械转换器的磁感应强度分布、激励电流、动态电磁力、位移等动态变化。

图5 COMSOL电-机械转换器实现电-磁-固耦合模型Fig.5 Electromagnetic-solid coupling model of electro-mechanical converter in COMSOL

软磁材料内部的磁化性能会在磁化过程中体现出来，工程中通常运用磁化曲线和磁滞回线2种方法进行模拟[13]。电-机械转换器开关过程是典型的磁性材料磁化和退磁过程，电工纯铁B-H磁化曲线如图6所示。B-H磁化曲线无法精确地拟合动态的磁化情况，尤其是在电-机械转换器受高频激励的工作场合，与实际的磁化情况有较大的偏差。因此，提出以J-A磁滞模型[14-15]模拟电工纯铁的磁滞特性，求解5 个基本参数[16-20]代入COMSOL 中建立模型，得到动态磁滞回线如图7 所示。从图7可以看出：铁磁性物质的第一次磁化沿着非磁滞线进行，退磁曲线和下一次的磁化曲线会形成1个回环。

图6 电工纯铁的磁化曲线Fig.6 Magnetization curve of electrical pure iron

图7 动态磁滞回线Fig.7 Dynamic hysteresis curves

2.3 动态磁滞响应结果分析

为进一步分析磁滞特性对开关响应性能的影响，在建立的COMSOL的磁化模型中分别设置BH磁化曲线模型和J-A动态磁滞模型，并进行仿真对比。2种转换器模型得到的激励和响应曲线如图8所示。从图8可以看出：B-H磁化模型下的最大电磁力为34.2 N，J-A磁滞模型下的最大电磁力为35.8 N，比前者大1.6 N。2 种模型的电-机械转换器的电气延迟时间均为0.65 ms，运动时间为1.50 ms，总时间为2.15 ms。B-H磁化模型下的电-机械转换器关闭时间为2.60 ms，J-A磁滞模型的关闭运动时间为2.73 ms，两者相差0.13 ms。产生以上现象的原因是J-A磁滞模型模拟了实际软磁材料退磁时存在磁滞现象，相比于B-H磁化模型，它的磁感应强度无法完全随电流的下降而下降。

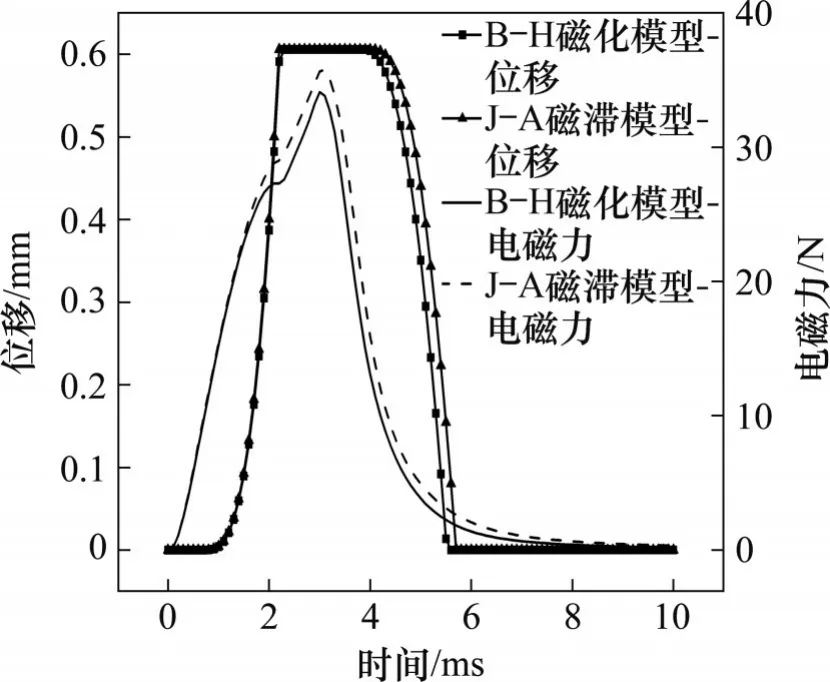
图8 J-A磁滞模型和B-H磁化模型电磁力和位移曲线Fig.8 Electromagnetic force and displacement curves of J-A and B-H model

3 模型验证

3.1 电磁力测试试验台的搭建

为验证融合磁滞的COMSOL 多物理场仿真模型的准确性，加工转换器样机，激励线圈的直径为0.7 mm，匝数为200，样机工作气隙为0.6 mm，整机外径为29 mm，长为45 mm，符合本项目对微小型转换器尺寸的技术要求；设计了静态电磁力测试试验台，其主要由电压激励装置、电-机械转换器样机、高精度微调节位移机械台、拉压式力传感器、电流传感器以及Labview 采集系统和Ni 采集卡组成，各传感器规格见表2。

表2 主要传感器的规格Table 2 Specifications of main sensors

电磁力测试试验台示意图如图9所示，样机和力传感器分别通过支撑固定架固定在X-Y轴移动台上，移动台通过锁紧机构进行固定。机械台由X-Y轴移动台、滑动导轨、固定支撑座组成，通过滑动导轨对样机和传感器相对位置进行调整并固定，微调节螺旋手柄对样机工作气隙进行调整。衔铁等运动部件通过螺纹与力传感器进行硬性连接。样机(无复位弹簧)和力传感器分别被固定安装在试验机械台上，能够直接测量电磁力随时间的动态变化，而不受弹簧预紧力的影响。线圈与电压激励装置相连，使线圈产生激励电流。

图9 电磁力测试试验台示意图Fig.9 Schematic diagram of electromagnetic force test bench

3.2 结果及分析

对电-机械转换器样机进行电磁力测试试验，将衔铁和力传感器固定连接，在不接外阻的条件下，线圈匝数为200，激励电压为15 V，激励时间为2 ms。实验测试和仿真结果对比如图10 所示。从图10 可见：实验和仿真的最大电磁力分别为57.440 N 和57.068 N，相对误差为0.65%，仿真比实验早0.1 ms到达峰值。实验测量的上升的电磁力曲线与仿真曲线较吻合，在电磁力下降阶段，实验曲线存在一定的抖动，仿真得到电磁力的下降时间为7.5 ms。对比仿真结果可以看出，电磁力的实验曲线与仿真曲线的变化趋势和幅值接近，表明了多物理场耦合电磁力仿真模型的准确性。

图10 激励时间2 ms时转换器的电磁力曲线对比Fig.10 Comparison of electromagnetic force variation curves of converts for excitation time of 2 ms

4 影响因素及优化分析

4.1 电气参数的影响

电-机械转换器的电气参数包括匝数、电流、电压等。在电压为15 V、激励时间为3 ms 下，不同线圈匝数转换器的电流和电感变化曲线如图11所示，线圈匝数分别为160，180，200，220和240匝。从图11 可以看出：随着线圈匝数的增加，线圈电感在初始值从9×10-4H增加到2×10-3H。这是因为在衔铁运动过程中，磁路的总磁阻减小，导致电感增大，完全开启时的电感从1.6×10-3H增加到3.6×10-3H；在相同的激励时间下，电感越大，电流变化越慢，导致最大电流越小。

图11 不同匝数转换器的电流和电感曲线Fig.11 Current and inductance of converts of different turns

不同匝数转换器的电磁力和位移曲线如图12所示。从图12 可见：在激励的5 ms 内，线圈匝数越多，最大电磁力也越大。但从局部放大图可以看到，匝数增多使得电流一开始上升速度较慢，导致电磁力上升越慢。这是因为线圈匝数增加不仅会使总磁通量增加，也会使得总磁阻增大；随着匝数的增加，开启响应时间从2.5 ms 缩短至2.1 ms；开启保持时间由于电磁力的增大而延长，但对关闭运动时间几乎没有影响。这是因为总磁通量的增大量始终大于总磁阻的增大量，因此，匝数越多，开启响应时间越短；但随着匝数的增加，对频响的提升率越来越小，同时，匝数增加会使线圈容腔体积与散热间隙发生变化，结合仿真结果与理论分析，设计线圈的匝数取220左右，综合效益最好。

图12 不同匝数转换器的电磁力和位移曲线Fig.12 Electromagnetic force and displacement of converts with different turns

不同电压激励下电磁力线和位移曲线如图13所示。从图13 可以看出：在不同激励电压下，激励时间均为3 ms；线圈两端电压越大，电磁力越大，最大电磁力从23.55 N 上升到107.30 N，达到最大电磁力的时间也越短。这是因为线圈两端的电压越大，产生的电场强度越大，磁感应强度越强，衔铁受到的电磁力也就越大；随着电压增加，开启响应时间从2.7 ms缩短至1.4 ms。激励电压升高使电流的上升速度和最大电流都得到提升；磁场强度快速上升在转换器中产生电磁吸力，且在磁轭的磁感应强度饱和前，激励电流越大，电磁吸力越大；电磁力的大幅度增大使得开启时间缩短，开启保持时间延长，但关闭运动时间几乎不变。由于纯铁DT4 的电导率较高，约为9.93×106m·Ω，仿真可得15，18，24，36 V 激励0.3 ms 时产生的涡流密度分别为24.32，32.83，36.58 和47.24 A/mm2，方向与激励电流的方向相反。因此，通过高压来增大转换器的频响，反而会产生显著的涡流损耗，设计时，激励电压应尽可能小，取值在12～15 V之间。

图13 不同激励电压下电磁力和位移曲线Fig.13 Electromagnetic force and displacement curves under different excitation voltages

4.2 结构参数的影响

4.2.1 弹簧刚度

电-机械转换器关闭时所产生的复位力是由弹簧预紧力和开启过程中的压缩力所提供的。弹簧刚度系数对于启动与关闭阶段的作用是相反的；在开启段，由于弹簧刚度的存在，弹簧进一步产生压缩力。弹簧起阻碍作用影响运动部件的加速度，导致开启时间变长；在关闭段，压缩力能提供更大的关闭加速度，从而缩短关闭时间。不同弹簧刚度下位移曲线如图14 所示。从图14 可见：随着弹簧刚度增加，开启时间几乎没有明显变化，这是由于微小型电-机械转换器的工作气隙极小，不同弹簧系数的仿真运动过程产生弹簧阻力差值相较于电磁力而言较小，因此，几乎对开启的动态特性没有影响。但是，在关闭阶段，衔铁运动基本由弹簧力主导，因此，关闭时间缩短显著。从图14 还可以看到：与弹簧刚度系数8 N/mm 相比，弹簧刚度系数14 N/mm 时的关闭时间缩短了0.3 ms。但需要注意的是，弹簧刚度过大会导致衔铁无法完全开启。因此，本文选择弹簧刚度系数在8～14 N/mm 范围内，适当增大弹簧刚度以减少开启和关闭的总时间。

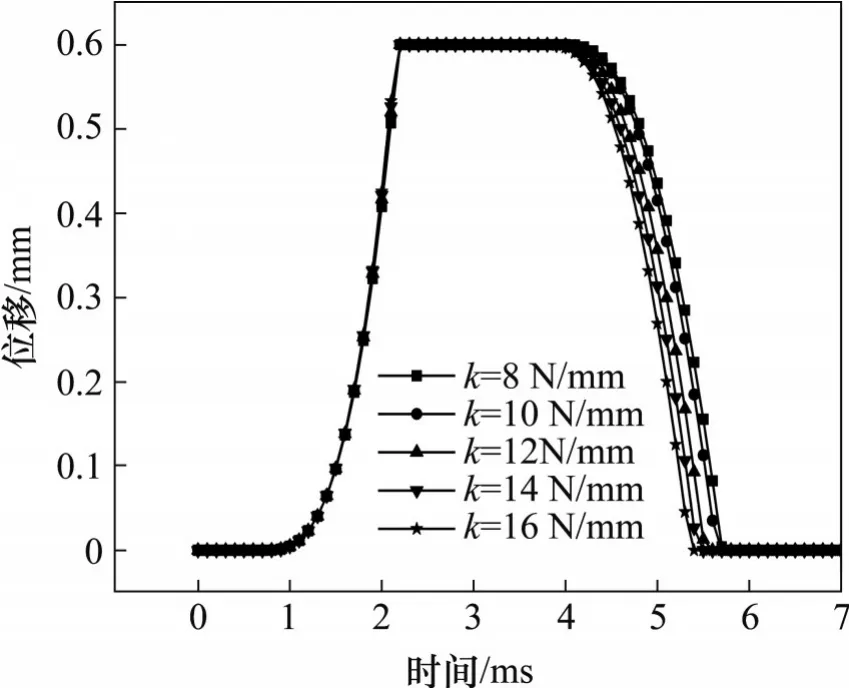
图14 不同弹簧刚度下位移曲线Fig.14 Displacement curves under different spring stiffness

4.2.2 衔铁长度及质量

衔铁长度的改变会引起磁路的变化从而影响频响。原设计的衔铁长度为10.8 mm，现分别缩短至9.8，8.8，7.8，6.8 mm。不同衔铁长度的电磁力曲线和位移曲线如图15 所示。从图15(a)可以看出：当衔铁长度为10.8 mm时，最大电磁力为34.96 N，随着衔铁长度的减小，电磁力依次减少0.44，1.02，2.01 和3.37 N。这是由于衔铁长度的缩短使得衔铁中心距离主磁极中心越来越远，磁场强度有所下降，减缓了电磁力的上升速度。值得注意的是，衔铁长度每缩短1 mm，衔铁质量从16 g 减少到2.9 g 左右；而质量减小有利于减小惯性力。从图15(b)可见：当衔铁长度为10.8 mm 时，开启响应时间为2.24 ms，关闭时间为1.64 ms；随着衔铁长度减小，开启响应时间依次缩短了0.04，0.10，0.15 和0.20 ms，关闭时间分别减少了0.11，0.21，0.32 和0.39 ms。这是因为在开启时间段内，改变衔铁长度带来的两种效果叠加后，质量减小起主导作用，因此，衔铁长度越短耗时缩短；同时，后半段主要由弹簧力复位衔铁质量减少带来的响应速度提升更加显著。推杆的螺纹装配长度为6 mm，考虑到安全性，在8～10.8 mm 范围内适当减小衔铁的长度，以减少开关时间。

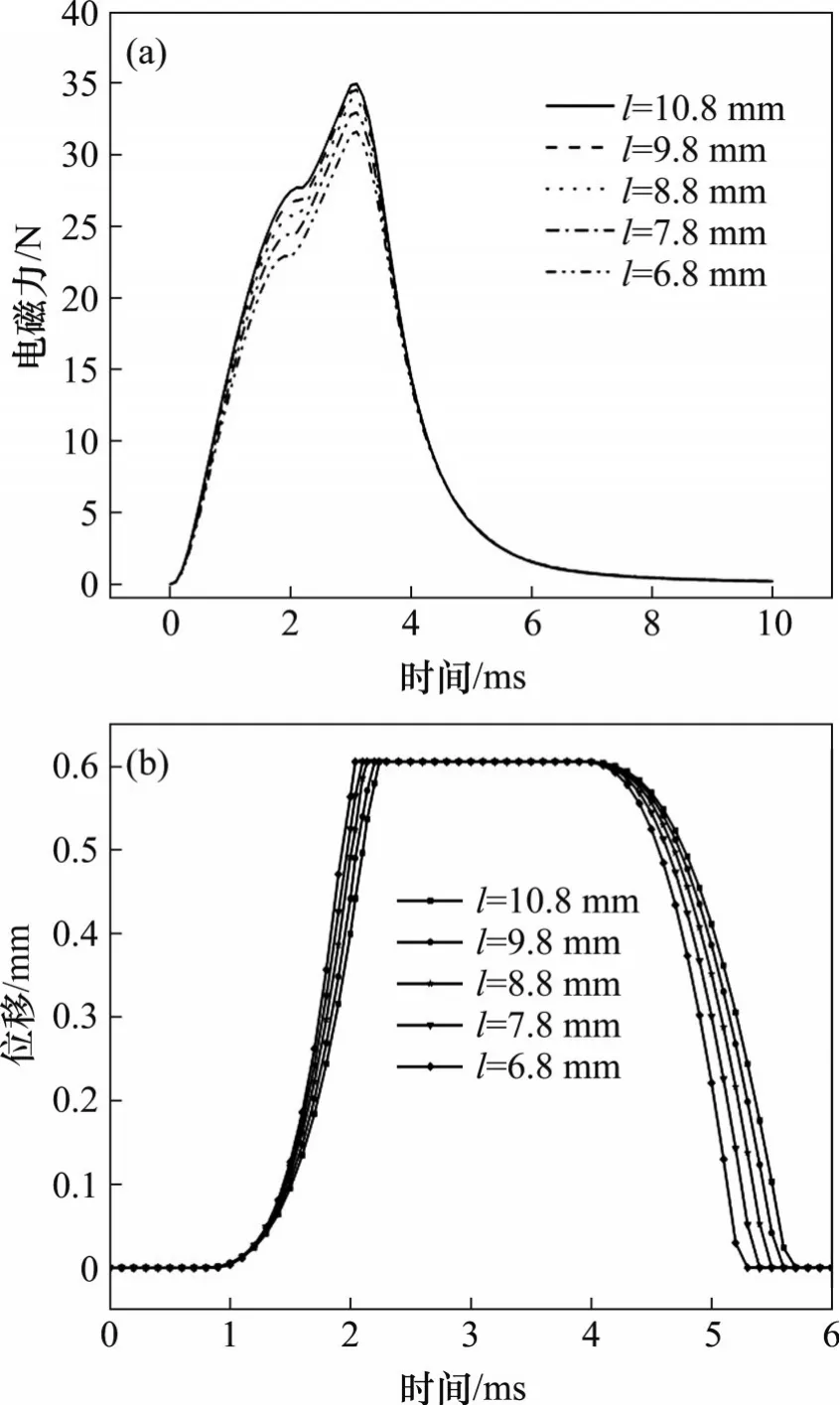
图15 不同衔铁长度转换器的电磁力曲线和位移曲线Fig.15 Electromagnetic force and displacement curves of converts with different armature lengths

4.2.3 工作气隙

工作气隙决定了衔铁的工作行程。在不同工作气隙下，激励同种电流的静态电磁力变化曲线如图16所示。从图16可见：当工作气隙从0.2 mm增大到0.6 mm 时，最大电磁力从51.14 N 下降至19.23 N。这是由于工作气隙直接影响气隙的磁阻和软磁材料的磁阻，而软磁材料的磁导率远远大于空气的磁导率，因此，随着工作气隙的增大，总磁阻会显著增大，导致电磁力减小。

图16 不同工作气隙转换器的电磁力曲线Fig.16 Electromagnetic force of converts at different working air gaps

不同气隙转换器的开启关闭时间如表3 所示。从表3 可以看到：当工作气隙从0.2 mm 增大到0.6 mm 时，开启时间从1.37 ms 增加至2.64 ms，关闭时间从2.45 ms增加至2.94 ms。因此，通过增加阀芯位移来提升流量的方法，在一定程度上会影响高速开关阀的启闭时间。

表3 不同工作气隙转换器的开启关闭时间Table 3 Open and close time of converts at different working air gaps

5 结论

1) 与B-H曲线模型相比，本文建立的融合磁滞的电-机械转换器多场耦合模型仿真得到的电磁力大1.6 N，更接近实际实验值，同时，该模型的关闭运动时间存在一定延迟。

2) 激励电压对频响的影响显著，但考虑涡流损耗带来的巨大温升，电-机械转化器的激励电压不宜过大，应控制在12～15 V之间；增加衔铁长度会使所受电磁力越大，运动质量也增大，减小衔铁长度带来的增益更大，衔铁长度取值范围为8.0～10.8 mm，线圈匝数选取220，弹簧刚度范围为8～14 N/mm。对于不要求大流量的高速开关阀，应尽量降低电-机械转换器的工作气隙来提升阀的响应性能，使得电-机械转换器达到最理想的频响。