新型多旋翼无人机结构设计及其控制系统算法

赵俊杰，束攀峰

（江苏理工学院 电气信息工程学院，江苏 常州 213001）

近年来，多旋翼无人机得到了深入的研究，其广泛应用于基础设施检测、灾害情况检测等危险或繁琐的活动中。无人机有升降、左右、前后线运动以及俯仰、横滚和偏航角运动，对于其位置控制[1-3]和姿态控制的研究较多[4-7]。传统多旋翼无人机具有同一特点，即每个旋翼轴线都是平行的，并垂直于机身平面，因此，只能提供四个有效控制分量：垂直于机身的升力；俯仰扭矩；横滚扭矩；偏航扭矩。为了实现前后、左右线运动，就需要对上述四个控制分量加以组合，因此，传统多旋翼无人机是一种多输入多输出、非线性、强耦合的欠驱动系统[7]。因为强耦合特性，飞行控制算法需要通过完成无人机的姿态控制才能实现其位置控制，而不能独立控制无人机的位置（只有处于水平姿态时，才能实现原地盘旋）。当前，无人机越来越多地被用作服务机器人，对于与环境的交互，这种移动性的丧失成为无人机应用的一个限制因素[8]。Ryll[8]提出了一种新型全驱动四旋翼无人机的结构设计和控制算法，在无人机的每个机臂上增设了可独立转动的舵机以调整每个驱动电机的角度，从而实现了无人机六自由度独立可控；但这种设计明显增加了结构的复杂性和控制难度。

为了解决上述问题，本文提出了一种新型多旋翼无人机结构设计及其飞行控制算法。新型多旋翼无人机需要有八个以上的驱动旋翼，并且旋翼转轴轴线和机身应成一定角度向内或者向外倾斜设置，通过旋翼推力组合可以独立实现向前、向后、向左、向右和向上的驱动力，以及俯仰、横滚和偏航扭矩；因此，其可以实现六自由度独立可控，而不需要进行解耦运算，也不需要线运动和姿态运动的内外环控制，即能够独立控制线运动和角运动。新型多旋翼无人机只需控制驱动电机的转速就可以直接进行位置控制，其响应可以更快，能更好地提高操控性能。由于线运动和角运动可以独立控制，其可以在一定的角度范围内以任意姿态角进行位置操控，这对于一些特殊的操控需求，比如定点摄影摄像、基础设施的定点检查等都是非常有利的。

针对多旋翼无人机模型中存在非线性因素和不确定参数的控制问题，鲁棒控制[9-12]、自适应控制[13-15]等很多控制算法得到了广泛应用。为了实现新型多旋翼无人机的飞行控制，本文设计了基于自适应控制理论的新型全驱动多旋翼无人机的位姿控制算法。首先，基于新型多旋翼无人机的线运动和角运动动力学方程，建立了全驱动动力学方程；然后，基于Lyapunov稳定性理论和自适应控制理论，设计了自适应控制算法；最后，在Mat-Lab上验证了新型多旋翼无人机的飞行性能和自适应控制算法的有效性。

1 新型多旋翼无人机的数学模型

新型多旋翼无人机的动力学模型具有多输入多输出、六自由度独立可控的特点。如图1所示，新型多旋翼无人机拥有八个独立驱动旋翼（拥有八个以上旋翼的无人机也可以应用同样的方法），每个电机和机身平面成一定角度θk向内或向外倾斜固定安装。如图2所示为旋翼结构。图2（a）为旋翼向外倾斜，图2（b）为旋翼向内倾斜。

图1 新型多旋翼无人机结构示意图

图2 旋翼结构示意图

需要指出的是，本研究所针对的多旋翼无人机的旋翼倾斜角安排，也可以旋翼全部向内倾斜或者全部向外倾斜，只需满足结构上左右对称即可；另外，为了近似于常见多旋翼无人机结构，倾斜角度θk选择θk∈[ π/4 0]。

为了建立数学模型，先建立如图1所示机体坐标系B和惯性坐标系E。图1显示，机体坐标系固定于无人机机身上，原点和无人机机身几何中心重合，坐标轴zb垂直于机体平面，坐标轴xb和yb分别与机臂平行。为了描述无人机的轨迹追踪运动，在惯性坐标系中机体坐标系原点的坐标为X=[x,y,z]T，机体坐标系的姿态为Θ=[ϕ,θ,ψ]T，在机体坐标系下多旋翼无人机转动角速度为ω=[p,q,r]T。为了能建立起新型无人机全驱动动力学方程，单个旋翼的推力有如下推力分量：

其中：θk是旋翼相对于机身平面的倾斜角；kb和ωi分别是旋翼的推力系数和转速；fiv(t)和fil(t)分别是平行于zb和平行于电机所在机臂的推力分量。因此，得到多旋翼无人机机体坐标系上推力分量为：

其中，fbx、fby和fbz分别是机体坐标系xb、yb和zb方向上的合成推力分量。由式（1）可得在惯性坐标系中多旋翼无人机的线运动动力学方程为：

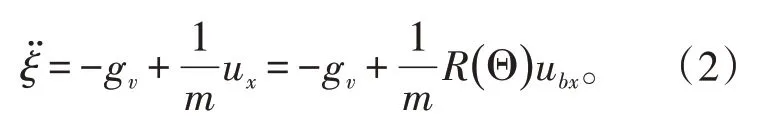
其中：

fx、fy和fz分别是惯性坐标系x、y和z轴方向上的合成推力分量；R()Θ是由机体坐标系至惯性坐标系的正交旋转变换矩阵。将式（2）代入式（1）后，可得到：

其中：sθk=sinθk；cθk=cosθk。需要指出的是，为了能够实现多旋翼无人机线运动的三自由度独立可控，驱动矩阵A1是行满秩矩阵。传统的多旋翼无人机只能在Zb方向有推力，其线运动动力学方程驱动矩阵的秩为1，非满秩矩阵，需要借助满秩矩阵R(Θ)才能实现三自由度可控；因此，传统多旋翼无人机的线运动和角运动是强耦合关系。新型多旋翼无人机的角运动驱动扭矩为：

其中：

kd是旋翼的阻力系数；τbx、τby和τbz分别是机体坐标系xb、yb和zb轴方向上的合成扭矩分量。虽然kb和kd是未知数，但kb/kd假定为固定的已知量。根据上式可得多旋翼无人机的角运动动力学方程为：

其中：J=diag[Jx Jy Jz]；ω=[p q r]T。

根据上式可得：

其中：

A2∈R3×8是行满秩矩阵。因此，新款多旋翼无人机的角运动是三自由度独立可控的。

由上述线运动动力学方程（3）和角运动动力学方程（4），可得新型多旋翼无人机的全驱动动力学方程为：

其中：

I3∈R3×3是单位矩阵；A3∈R6×8是行满秩矩阵。多旋翼无人机的角速度ω(t)和惯性坐标系欧拉角Θ(t)有如下的关系：

其中：

03∈R3×3是单位零矩阵；ξg=[x y z ϕ θ ψ]T是无人机实时位姿信号。

为了在惯性坐标系中描述新型多旋翼无人机的六自由度动力学方程，由式（5）和式（6）可得到：

2 目标位姿信号追踪控制算法设计

为了设计新型多旋翼无人机的六自由度控制

算法，引入目标位姿信号ξgd，并且其一阶和二阶微分信号同样是连续有界信号。无人机的轨迹追踪误差信号为为了设计轨迹追踪控制算法，引入新的误差信号其中，α是正的设计参数。如果误差信号e(t)趋于0，则也将趋于0，就能实现追踪目标位姿信号的目的。e(t)的一阶微分为：其中：

ΘmkJ是包含了未知参数的矩阵；ξk是包含已知信号的向量；um是包含电机转速的向量。为了实现自适应控制，设计如下自适应控制算法：

将式（8）代入式（7）后，可得：

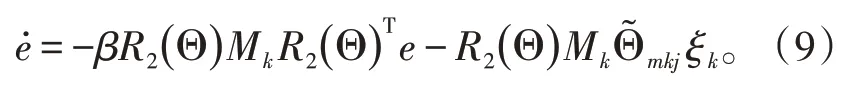
为了验证误差信号e(t)和的收敛性，设计了正值函数，代入式（9）得到其一阶微分如下：

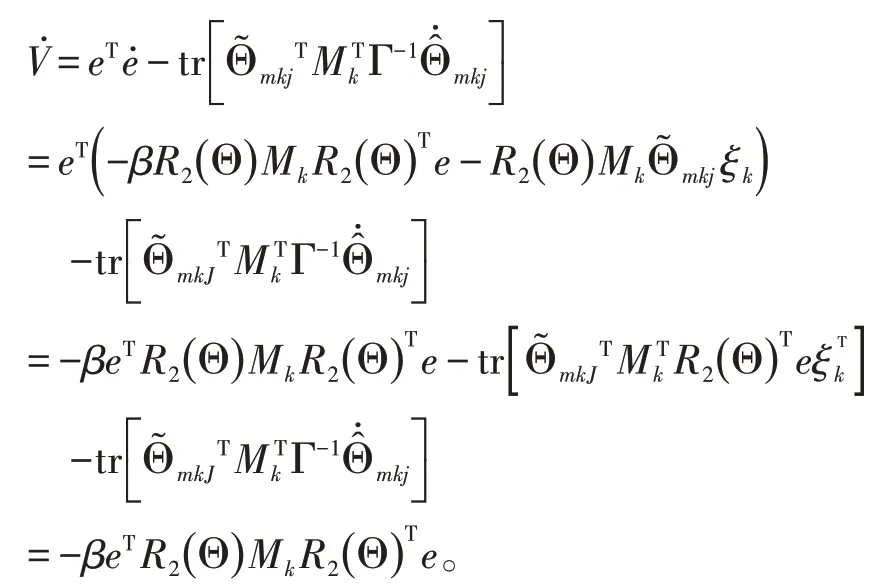
由上式可得：e(t)为渐进稳定；为有界稳定。因此，也将渐进稳定，即无人机实际位姿信号ξg能够追踪目标位姿信号ξgd。

3 仿真与结果分析

为了验证新型无人机结构设计和控制算法的有效性，使用Simulink建立新型多旋翼无人机的数学模型和控制器。如表1所示，为新型多旋翼无人机模型参数值和实际参数值。表1显示二者有一定的误差。

表1 多旋翼无人机模型参数

控制器中参数设置为α=40、β=400、Γ=I6。为了验证新型无人机的六自由度独立可控特性，设计了如下三种验证状况。

（1）目标位姿信号ξgd中姿态信号不变，位置信号变化如图3所示。位置三自由度的信号分别

图3 姿态信号不变，目标位置信号对应的轨迹

图4 姿态信号不变，目标位姿信号和实际位姿信号

图5 位置信号不变，目标位姿信号和实际位姿信号

（3）目标位姿信号ξgd中位置信号和姿态信号同时独立变化，如图6所示。位置三自由度的信号分别显示在图7（a）图7（c）和图7（e）中，其中，虚线显示的是目标位置信号，实线显示的是实际位置信号。姿态三自由度的信号分别显示在图7（b）图7（d）和图7（f）中，其中，虚线显示的是目标姿态信号，实线显示的是实际姿态信号。可以看出，新型无人机可以实现六自由度独立可控运动。

图6 位置信号和姿态信号同时独立变化，目标位置信号对应的轨迹

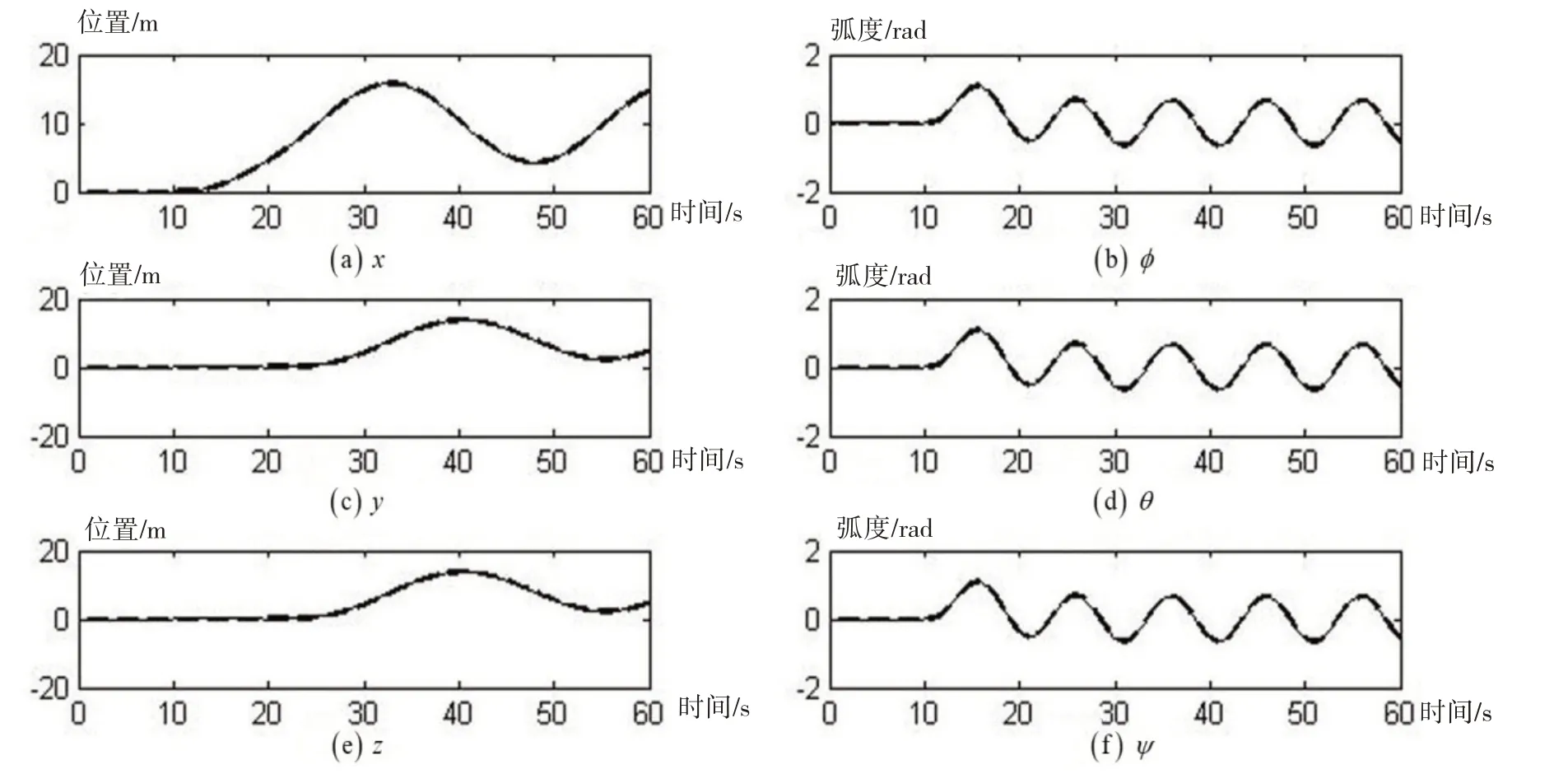
图7 位置信号和姿态信号同时独立变化，目标位姿信号和实际位姿信号

4 结论

针对传统多旋翼无人机的线运动和角运动是强耦合关系，不能实现六自由度独立可控的问题，本文提出了一种新型多旋翼无人机六自由度独立可控结构设计以及相应的飞行控制算法。新型多旋翼无人飞行器由八个独立驱动电机驱动旋翼，和机身平面成一定的夹角排列，实现了六自由度独立可控运动。利用自适应控制算法，实现了新型多旋翼无人飞行器的轨道追踪控制和姿态控制，并仿真验证了控制算法的有效性。