基于M序列编码的平面磁感应式角度传感器研究

石洪

连云港杰瑞电子有限公司

1 引言

平面磁感应式角度传感器是一种基于磁感应原理并采用PCB工艺制作的传感器[1]。该传感器既具有传统旋转变压器类磁感应传感器的优点，如抗干扰能力强及环境适应性好，并且由于采用PCB工艺，传感器的体积更小、重量更轻，因此广泛应用于工业、航空、国防等空间狭窄及环境恶劣的场合[2-4]。

目前平面磁感应式角度传感器大多采用游标编码方式获取绝对位置，解算时需要粗精通道的精度误差不能超过纠错范围[5]。然而，随着高精度平面磁感应式角度传感器的极对数增加，纠错范围急剧减小，导致传感器使用过程中容易出现角度跳变的问题[6，7]。鉴于此，本文提出了一种基于M序列的平面磁感应式角度传感器的编码方法，可以实现平面磁感应式角度传感器的绝对位置测量，并提升传感器的纠错范围。

2 游标式平面磁感应角度传感器结构及工作原理

游标式平面磁感应角度传感器由定子与转子两部分组成，结构如图1所示。其中，定子由环形激励线圈EX、粗通道正弦接收线圈C_sin、粗通道余弦接收线圈C_cos、精通道正弦接收线圈F_sin和精通道余弦接收线圈F_cos五部分组成。粗精通道的正弦接收线圈与余弦接收线圈在空间角度上分别相差1/4周期。粗精通道的正、余弦线圈的周期数互为质数。转子部分由内外环两路铜箔阵列组成，铜箔阵列的周期分别与粗精通道的正余弦线圈的周期一致[8-10]。

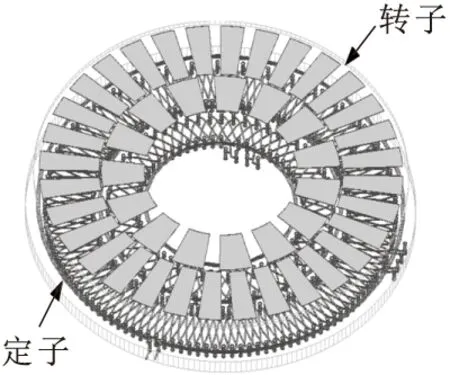
(a)总体结构

定子的环形激励线圈注入交变信号U(t)=Umsin(ωt)时，将会产生一个环形时变磁场，而转子的铜箔在该时变磁场中将会产生涡流，影响磁场分布[11]。当传感器转子转动时，根据法拉第电磁感应定律，此时精通道正、余弦接收线圈产生的感应电动势与转子转动角度θ相关，具体为

ec_sin(t，θ)=kcsin(mθ)sin(ωt)
ec_cos(t，θ)=kccos(mθ)sin(ωt)
eF_sin(t，θ)=kFsin(nθ)sin(ωt)
eF_cos(t，θ)=kFcos(nθ)sin(ωt)

(1)

式中，m和n分别为粗、精通道的线圈周期数；kc和kF为粗、精通道的线圈耦合系数。

将粗、精通道的四路模拟信号经过检波、滤波可以获得不含载波的模拟信号，为

(2)

式中，θc和θF为粗、精通道模拟信号检波后的相位角。

且θc和θF与转子转动角度θ的关系为

ic×2π+θc=mθ
iF×2π+θF=nθ

(3)

式中，ic和iF为粗、精通道模拟信号随着转子转动角度θ变化的周期。

式(2)中的模拟信号经过ADC采集，再进行反正切计算，即可求得粗精通道模拟信号检波后的相位角θc和θF，有

(4)

根据求取的相位角θc和θF，可以计算出精通道模拟信号变化周期iF，有

(5)

式中，mod()为取余函数。

将式(4)和式(5)代入式(3)中，即可获得传感器转子转动角度θ，有

(6)

实际使用过程中，由于制造、安装等影响，求取的相位角θc和θF均存在一定误差，设其分别为Δθc和ΔθF，为了避免iF计算错误导致转子转动角度θ出现粗大误差，根据式(5)可以推出Δθc和ΔθF需要满足以下的纠错范围。

iF×2π-πiF×2π+π>m(θF+ΔθF)-n(θc+Δθc)

(7)

将式(7)进行化简，可得

(8)

由式(8)可知，基于游标编码的平面磁感应式角度传感器的纠错范围随着传感器的极对数增加而减小。另一方面，为了提高传感器的精度，必须增加传感器的极对数，因而游标编码限制了平面磁感应角度传感器向高精度方向的发展。

3 M序列编码的平面磁感应角度传感器结构及工作原理

3.1 M序列的原理及编码方法

M序列是最长线性反馈移位寄存器序列的简称，该编码方式具有循环性和可预测性的特点[12]。如图2所示，通过a0，a1，…，an-1的n级串联移位寄存器和c0，c1，…，cn的反馈逻辑线路可构成M序列发生器，图中，c0，c1，…，cn的取值为0或1，分别表示反馈线路的断开和接通。在脉冲信号的控制下，所有寄存器的值通过反馈回路进行模2的加法运算获取an的值，同时各个寄存器中的值也依次传递到下一级的寄存器中[13-15]。

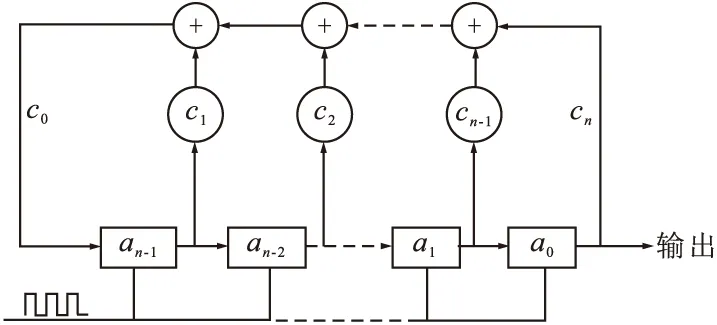
图2 线性移位寄存器原理

图2中的逻辑表达式为

(9)

如果c0，c1，…，cn的取值满足式(10)所示的n阶本原多项式，即可生成循环周期为2n-1的M序列[16]，有

(10)

以4阶的M序列为例，其本原多项式为

F(x)=x4+x1+1

(11)

将寄存器a1～a4的初始值设置为0001，由此生成的15位M序列编码为000111101011001。实际应用过程中，为了保证编码器角度的连续性，需要在M序列中的起始点再加入一个0，构成16位的编码0000111101011001。

3.2 M序列编码在平面磁感应式角度传感器的应用

基于M序列的平面磁感应式角度传感器采用4阶的M序列编码方式，传感器结构如图3所示。传感器由定子与转子两部分组成，转子部分由内外环两路铜箔阵列组成，定子由精通道激励线圈EX、精通道正弦接收线圈Rsin、精通道余弦接收线圈Rcos、粗通道激励线圈E1～E8、粗通道接收线圈R1～R8、粗通道磁场补偿线圈K1～K4六部分组成[17]。

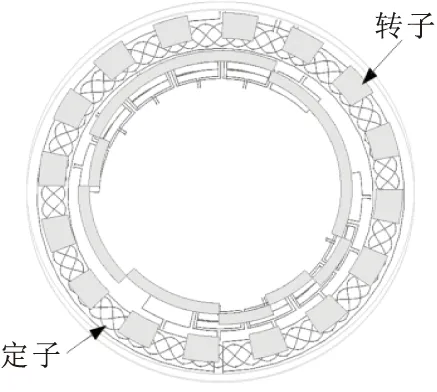
(a)总体结构

传感器的精通道结构及工作原理与前述游标编码一致，此处不再赘述。传感器的粗通道采用差分的M序列进行编码，如图3c所示，粗通道接收线圈R1～R8的接收区域划分为T1、T2两个区域，并反相连接。同时转子的粗通道铜箔也划分为两个区域，如图3b所示，分别按照1111000010100110及0000111101011001进行敷铜，其中，0表示敷铜区域，1表示不敷铜区。

粗通道激励线圈E1～E8注入交变信号U(t)=Umsin(ωt)时，将会分别产生一个时变磁场，而转子的铜箔在该时变磁场中将会产生涡流，影响磁场分布。粗通道接收线圈R1～R8随着转子铜箔的转动，产生变化的感应电动势。

接收线圈R1～R8除了受到激励线圈E1～E8的磁场影响外，还会受到临近激励线圈的磁场影响，其中线圈R1、R4、R5、R8由于临近激励线圈的数量与其他粗通道接收线圈不一致，导致其磁场强度相对较弱。为了保证粗通道接收线圈R1、R4、R5、R8产生的感应电动势与其他接收线圈一致，在其外围再各加一个用于平衡磁场强度的补偿线圈K1～K4。当补偿线圈K1～K4也注入交变信号U(t)=Umsin(ωt)时，接收线圈R1～R4中线的磁场强度补偿前后对比如图4所示。

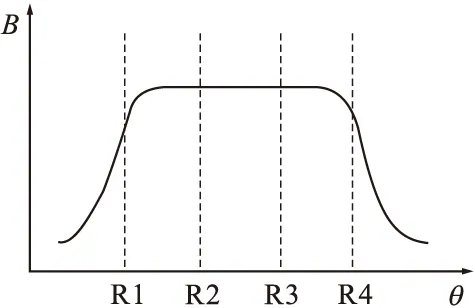
(a) 补偿前

以接收线圈R1为例，根据法拉第电磁感应定律，接收线圈R1的T1、T2两个区域产生的感应电势为

(12)

式中，k1和k2分别为无铜箔覆盖区域的接收线圈耦合系数和有铜箔覆盖区域的接收线圈耦合系数；ST1和ST2为T1和T2两个区域的总面积；θT1和θT2分别为T1和T2被铜箔覆盖区域的夹角。

将两路信号叠加即可得到接收线圈R1的最终输出电信号，为

eR1(t，θT1)=eT1(t，θT1)+eT2(t，θT2)

(13)

对粗通道接收线圈R1进行磁场仿真，其中交变信号U(t)的幅值设置为3.3V，频率设置为2MHz，定转子间距设置为1mm，仿真结果如图5所示，图中0°与22.5°时的信号幅值不一致是由于ST1，ST2的夹角相同，但面积不相等。

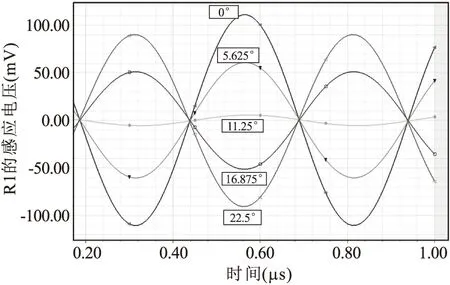
图5 接收线圈R1输出信号与转子的位置关系

由图5及式(12)可知，当T1、T2上方的转子铜箔为“01”时，R1输出最大正向电信号，该信号经过检波器、比较器处理，可以转换为逻辑“1”。而当T1、T2上方的转子铜箔为“10”时，R1输出最大反向电信号，该信号经过检波器、比较器处理，可以转换为逻辑“0”。

R1～R4四路接收线圈输出电压信号经过检波器、比较器处理，即可获得与转子转动角度θ相关的M编码，但这种码值不能直接使用，需要通过LUT(look-up-table)转换为二进制的粗通道角度θc，其关系如表1所示。将θc与精通道角度θF进行组合，获得转子转动角度θ。

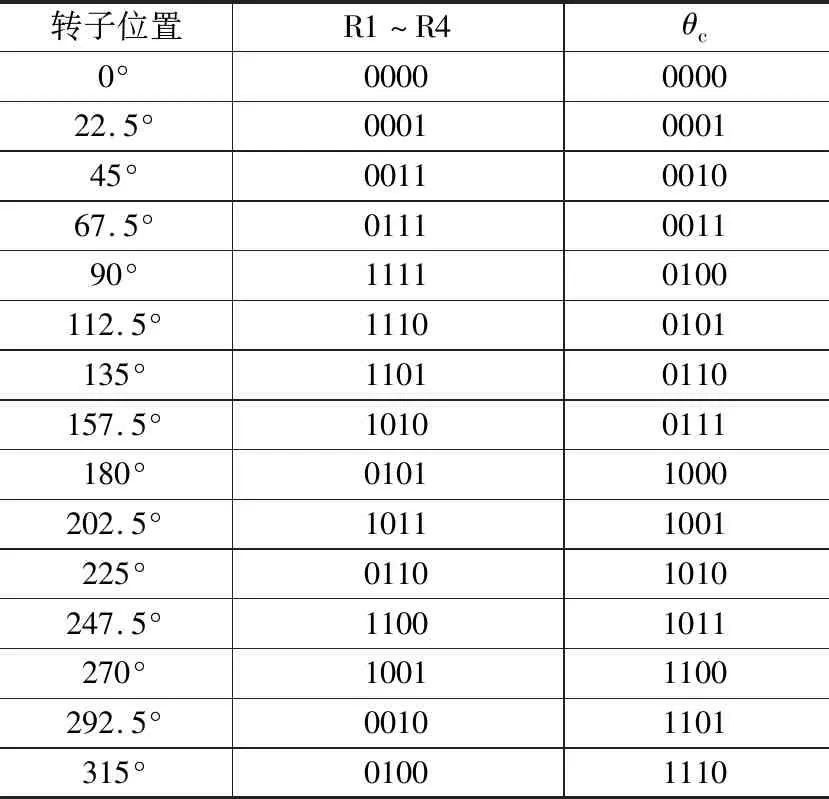
表1 转子位置与R1～R4输出关系

4 M序列编码的平面磁感应角度传感器的容错分析

传感器转子转动过程中，T1、T2区域上方的转子铜箔可能处于“10”与“01”的中间状态，由图5可知，此时R1～R4输出信号幅值较小，逻辑判断处于临界状态，直接读取R1～R4的M码值进行解算就会出现错误。针对该问题，提出一种双组接收线圈结构，即再增加一组R5～R8接收线圈，新增加的线圈与原来的线圈在空间上相差π-π/n，为便于理解，将线圈沿直线展开，其结构如图6所示。

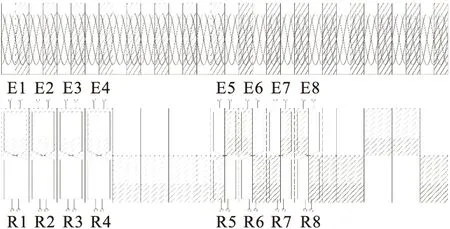
图6 双组接收线圈的相对位置关系

当接收线圈R1～R4接收信号处于临界状态时，线圈R5～R8输出信号处于稳定状态。因此θF在0～π/2或3π/2～2π时，FPGA选择读取R1～R4的M码值进行解算获得θc，而当θF在π/2～3π/2范围时，FPGA可以切换读取R5～R8的M码值进行解算获得θc。

不同于游标编码的绝对角度是通过粗精码道差值计算获得的，M编码的绝对角度直接通过读取R1～R4或R5～R8的码值获得，并且R1～R8是完全独立的线圈，只需要保证R1～R4或R5～R8各自读取的码值正确，基于M序列的平面磁感应式角度传感器就不会出现粗大误差。以接收线圈R4、R8为例，线圈输出电压信号的幅值与精通道角度θF的关系如图7所示。

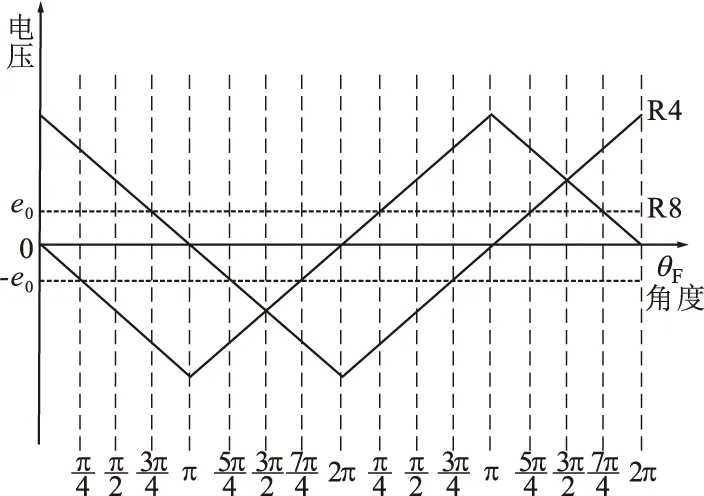
图7 接收线圈输出电压与精通道角度关系

由图7可知，设粗通道信号处理电路中的比较器阈值为e0，若粗精通道角度的误差只要满足下式要求，基于M序列的平面磁感应式角度传感器就不会出现粗大误差，即

(14)

对比式(8)和式(14)可知，在极对数较多的情况下，相比游标编码方式，M序列编码的纠错范围更大且更不容易出现粗大误差。

5 传感器样机和实验

5.1 样机与实验平台

根据上述传感器模型，分别设计了φ100mm游标编码和M序列编码的平面磁感应式角度传感器样机，如图8b所示，其中游标编码的传感器的粗精通道周期数量为3和32，而M序列编码的传感器粗精通道周期数量为8和32。搭建如图8a所示的实验平台，该实验平台采用九江精密测试技术研究所研制的TS-200型单轴速率位置转台(测量精度3″)为基准，待测传感器与转台同轴安装，通过上位机软件采集基准转台与传感器的角度进行对比分析[18]。

(a)测试系统

5.2 实验结果与讨论

为了比较不同安装偏心量下两种传感器受到的影响情况，对两种传感器的转子在不同安装偏心下的准确性进行对比测试。基准转台匀速转动，以1°的间隔采集传感器的数据，结果如图9所示。实验测得基于游标编码的传感器在0.15mm的偏心量下出现粗大误差，误差大概为90°，为精通道单周期角度的整数倍，并且随着偏心量的增加，出现误差的区间在逐渐增大。基于M编码的传感器在0.25mm的偏心量下出现粗大误差，误差大概为22.5°，为粗通道的最小单周期角度，并且出现误差的区间相比游标编码的更小。可以看出，基于M编码的传感器具有更宽容的安装要求，更不容易出现粗大误差。

图9 传感器在不同偏心量时的准确性

为了对比两种传感器的测量精度，将两种传感器的转子偏心量均调节到0mm，在0°～360°范围内，基准转台按照2°的间隔进行步进，分别采集两种传感器的输出角度与基准转台角度进行对比，传感器误差曲线如图10所示。实验测得，游标编码的传感器整周期误差为0″～12.5″，M编码的传感器整周期误差为0″～10″。由此可见，在相同的精通道周期数下，基于M序列编码的传感器与基于游标编码的传感器测量精度均可达±10″。

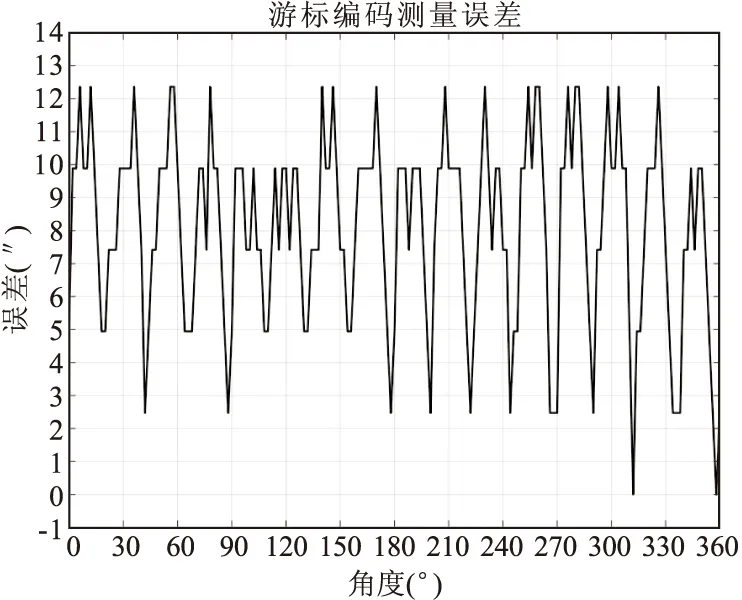
图10 传感器误差曲线

6 结语

目前平面磁感应式角度传感器的绝对编码方式较单一，本文提出了一种基于M序列编码的平面磁感应式角度传感器。传感器的粗码道采用差分的M序列编码方式，并通过双组接收线圈组合的方式，提高了传感器可靠性。

通过对比分析游标编码与M序列编码的纠错范围，表明在极对数较多的情况下，M序列编码方式纠错范围更大，更适合高精度的平面磁感应式角度传感器。

样机实测表明，基于M序列编码的平面磁感应式角度传感器的安装范围更宽，能够更好地实现可靠的绝对位置测量。因此，本文所研究的绝对编码方法为平面磁感应式角度传感器的编码方式提供了新思路。