短电弧铣削加工窄隙流场固液两相仿真及试验研究

吴敏，常星星，高茂洋，马浩骞

安徽天航机电有限公司

1 引言

随着科技与社会的发展，航空航天及深海技术对材料的要求越来越严格，针对超硬材料的加工多采用放电加工技术(EDM)等非传统的材料去除方式。王津[1]对连续放电过程中间隙内流场气、液、固进行三维仿真模拟计算，得出极间内气泡是蚀除物抛出间隙的主要因素；常伟杰等[2]对超声振动辅助电火花铣削流场进行了仿真研究发现，超声波可以减小加工间隙内颗粒的聚集同时使其分布更均匀，有利于排屑；黄青宇[3]基于电火花加工材料去除机理，探究了蚀除物运动规律，并结合FLUENT软件模拟得出抬刀运动是减小边角损耗的主要原因；何巍杨等[4]通过非电参数对短电弧加工的压力场、速度场的影响进行仿真发现，增大压力有利于提高加工效率；Jithin S.等[5]应用CFD软件模拟出电极跳变下加工间隙中流场，证明了电极跳变对加工中颗粒的分布影响较大；Tamang S.K.等[6]通过实验与FLUENT软件仿真计算，分析了蚀除颗粒在间隙中的分布情况符合Rosin-Rammler二态分布。因此，通过对放电加工间隙流场内蚀除物分布状态进行仿真分析，并得出其与工件加工速度和电极损耗的变化规律，对工艺的改进和加工参数的选取至关重要。

短电弧铣削加工技术原理是基于一定比例的气液混合工作介质下，当工件与工具之间的距离接近时，极间介质被电压击穿形成放电通道[7]，放电群组诱发产生的电弧热侵蚀将通过放电通道转移到工件表面。当一个电弧激发放热完成后，在脉冲电源的激励下，热源离子将诱导产生下一个电弧[8]，随着一连串的电弧与高压水气作用，受热的局部工件将熔化、凝固形成蚀除物，因此短电弧加工材料去除机制与电火花和高速电弧类似。其加工原理如图1所示。

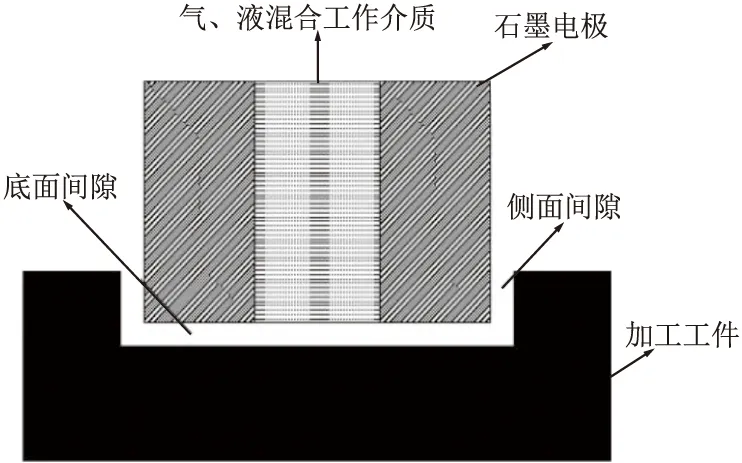
图1 短电弧加工原理

由于短电弧加工窄隙通常为微米级别，若蚀除物在加工过程中未及时排除，在间隙堆积会引起“二次放电”现象，导致加工条件恶化，甚至会出现短路状况，影响短电弧加工的稳定性和加工精度。研究窄隙中流场的运动规律可以提高材料去除率和加工工件表面精度，随着放电加工的进行，研究窄隙过程较复杂，难以用仪器直接测量计算出流场蚀除物运动情况，因此，需借助仿真软件对流场进行探索研究，并结合实验进行验证。

2 窄隙流场理论分析

为了简化理论分析，对短电弧间隙内流体作如下假设：①极间的流场仅考虑质量守恒和能量守恒，不考虑对热场和磁场的影响；②极间的流体为不可压缩且连续。

(1)质量守恒方程

间隙流场内流体质量守恒方程的微分形式为

式中，ρ为流体密度(kg/m3)；t为时间(s)；符号∇表示散度；v为速度矢量。

可以把∇(ρv)分解为x，y，z三个方向，即

式中，ux，uy，uz分别为x，y，z方向的速度分量(m/s)。

对于不可压缩流体，ρ为常数，则有

(2)颗粒运动方程

短电弧在加工过程中，蚀除物在间隙流场会在液体冲击力与重力的作用下运动，其空间三维运动方程为

式中，up为蚀除物运动速度(m/s)；u为流体的速度(m/s)；ρρ为蚀除物的密度(kg/mm3)；g为x方向的重力加速度(m/s2)。

(3)连续性方程

式中，U为工作液的平均速度(m/s)；η为工作液的动力黏度(kg/(m·s))；k为湍流能(m2/s2)；ε为湍动流扩散率(m2/s3)。

3 流场仿真模型及结果分析

3.1 仿真模型

为了提高本次仿真的准确性，对侧面窄隙与底面窄隙进行计算，侧面窄隙由加工后的轮廓直径减去加工前的电极直径获得，其差值的1/2即为侧面窄隙。

底面窄隙计算步骤为：在短电弧加工开始产生电弧时，记下数控显示柜上的z轴数据z0，把加工工件表面与工具底部表面上的附着物清理干净后，手动使电极与加工的工件底部轮廓相接触，记下z轴数据z1，两者差值的绝对值为底面窄隙。对于底面窄隙与侧面窄隙，采用三次实验进行测定求平均值，并结合电火花加工研究情况，得出底面间隙与侧面间隙均为0.1mm。采用合适的比例建立如图2所示几何模型。

图2 间隙流场几何模型

3.2 仿真分析

在ICEM中建立几何模型并进行网格划分，将划分好的网格导入FLUENT求解器中，并初始化边界条件，当计算结果合格时再采取后处理方式进行输出，若求解计算不合格，需检查边界条件或优化网格，直至得出合理结果。模型采用Simple算法处理连续相，工作介质气液混合选择Mixture模型，网格类型选择Cooper，边界条件为：入口处选用Velocity-inlet，出口为Pressure-outlet，其他边界设置为wall，试验中介质为液态水，密度为998kg/m3，黏度为1.005×10-3Pa·s，孔径为0.006mm，入口速度为1.5m/s，将数据代入计算得出雷诺数为8951，介于8000～12000之间，因此本实验仿真选择湍流模型。根据上面计算的雷诺数和实验中所用的数据可得进出口的湍流动能为0.0002m2/s2，一般在湍能计算中要求涡流黏性比分子大两个数量级或以上，取湍流耗散率为0.01m2/s3[9]。

图3为工具电极转速为400rad/s、入口介质压力为1.5MPa、加工深度为1mm的压力图。可以看出，工作液在电极内孔壁流动时，压力几乎无明显变化，在工件底面会形成一个明显的半圆弧形状区域。这是由于介质在拐角处短时间内会形成巨大的压力差，有利于侧面间隙的颗粒运动排除，同时当介质流入两边间隙时，压力逐渐减小直到与外界的大气压接触排除，此时压力值最小。为更好地探究不同加工深度时的压力变化，在图中从内壁右边缘处做垂直于工件表面的垂线，垂线与工件交点为a，逐渐向左边等距共取5点，分别为a，b，c，d，e，每点间距离为10μm，后文模型均按图3进行规定。

图3 间隙流场的压力云图(加工深度为1mm)

图4为加工深度分别为1mm，2mm，3mm，4mm各点上的压力图。由图可知，当加工深度改变时，流场的压力变化不明显，但从b点到a点时压力差较大，这是因为在a点处工作介质会转变方向由底面间隙流入侧面间隙；同时，在加工深度为3mm时，从e点到a点的压力差较大，这有利于间隙颗粒的排除和降低电极损耗。

图4 不同加工深度时的压力变化

图5为工具电极转速为400rad/s、入口介质压力为1.5MPa、加工深度为1mm的速度图。由于进口长度大于出口长度，对于相同体积的流体来说，入口处的速度相对于出口处较小，同时在拐角处的速度很小趋近于零，这是由于在加工过程中会有一部分蚀除物与电极损耗物聚集在一起形成颗粒，降低流体速度。

图5 间隙流场的速度云图(加工深度为1mm)

为进一步探究不同加工深度下的速度变化，图6为不同加工深度下的速度变化结果。在加工深度为3mm时，间隙内各点速度较大，当冲液速度大于颗粒蚀除物的自身重力时，颗粒会产生一定的加速度，有利于蚀除颗粒的排除，减小二次放电的发生。同时，从电极中心处间隙位置到侧面间隙流体的速度逐渐的增大，说明电极的中心边缘的颗粒堆积较小，有利于排屑。由动量守恒原理，在间隙的拐角处颗粒与壁面发生碰撞动能减小，即a点处的速度值降低。

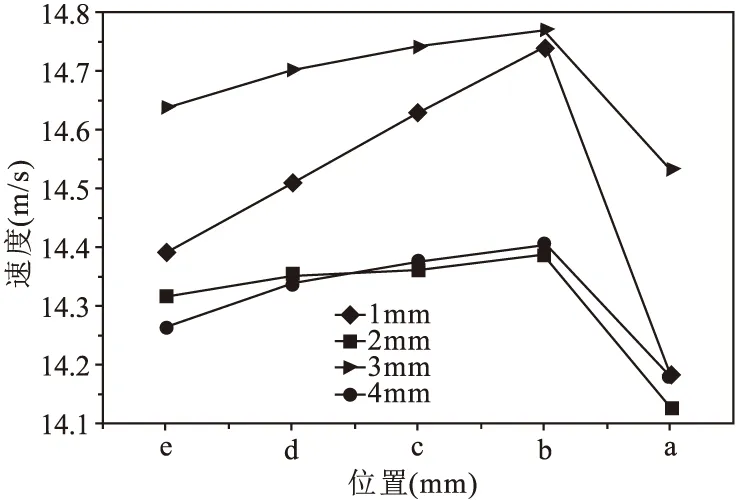
图6 不同加工深度下的速度变化

短电弧在加工过程中存在电极损耗，因此蚀除的颗粒会有所差异，工件铸铁的密度为7550kg/m3，石墨的密度为2250kg/m3，这里统一设置为惯性颗粒(steel)。

在连续相收敛后加入离散相颗粒，同时增加边界条件，设定出口和入口为escape模型。所有的wall为reflect边界条件，由恢复系数定义式为入射角与反射角的角度之比，当入射角与反射角相等时，比值为1，表示颗粒在壁面间碰撞时无动量和能量的损耗，因此设定reflect为常数且为1。等边界条件施加完毕后，将离散相颗粒的计算结果重新代入连续条件下进行迭代，重新计算流场的连续相，操作重复直至结果收敛。

图7为颗粒分布，可以明显地发现，粒子的富集区集中于拐角处，在电极的旋转与气液冲击下，越靠近电极的边缘处颗粒浓度越大。当粒子在狭小空间内不能及时被排除时，会增加活跃的粒子与电极碰撞的机率，因此导致电极损耗量增加，有效解释了短电弧在加工时工具存在“边角损耗”现象。

图7 粒子分布

图8为粒子停留时长与路径关系。可以看出，部分粒子在间隙中停留的时间相对较长，这些粒子会沉降在底面间隙与侧面间隙的拐角处，由于这些粒子在短时间不能有效排除，会增加“二次放电” 情况的发生，这对于工件精度有不利的影响，严重时会产生短路现象。为提高加工的稳定性，有必要减少这部分粒子的停留时间。

图8 粒子停留时长与路径关系

4 实验验证

在探究加工深度的变化对电极损耗率与加工工件的表面质量影响，选择电参数和非电参数时遵循统一的原则。实验采用正极性加工方式，工件为铸铁，工具为外径18mm的墨电极、内孔6mm的石墨，气液混合比150:1，电压为20V，占空比为60%，频率为1000Hz。图9为加工深度分别为1mm，2mm，3mm，4mm的工件。对加工的工件与电极进行处理计算，并采用显微观察其粗糙度，结果如图10所示。

(a)1mm

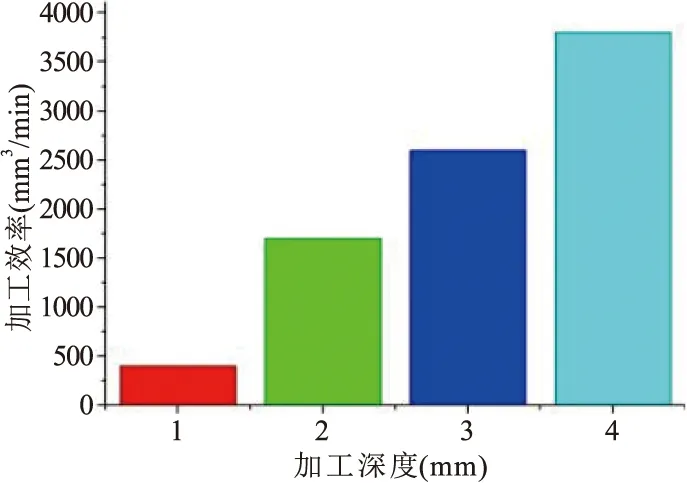
由图10可知，随着加工深度的增加，单位时间内材料的去除量变大，即加工效率明显增加，同时深度越大，蚀除颗粒在间隙内相对更难排除，增加与电极的碰撞机率，导致电极损耗加大，在加工深度为3mm时，电极相对损耗量最小，有利于加工的稳定性与可持续性，从流场的速度场与压力场分析可有效证明仿真结果的准确性。由于工件表面质量与电参数有很大关系，因此在非电参数下加工深度对粗糙度的影响不明显。

图10 加工效果

5 结语

流场仿真中间隙内颗粒分布比较均匀，在间隙的拐角处会形成富集区，由于颗粒停留的时间较长，会引起非正常放电加工，严重时会出现短路现象，同时增加与电极碰撞的机率，使得电极有着明显的“边角损耗”，即尖角变钝。

短电弧铣削加工深度增加时，加工效率明显提高，但对表面质量却没有很大改善，当加工深度为3mm时，颗粒在间隙内流动最快且有利于排屑，降低了粒子与电极之间的碰撞机率从而减小了电极损耗，有利于加工的稳定性与可持续性。