滑翔导弹轨迹跟踪与能量管理模型设计与仿真

尹中杰，王 磊，施振兴，王韦钰，杨建东，蔡克荣

（上海机电工程研究所，上海 201109）

随着高超声速技术的发展，以美国为代表的军事大国正在大力发展临近空间高超声速飞行器，并在完成一系列的飞行试验后提出了武器化的HSSW、AHW等项目，其中滑翔类项目因具有响应时间短、飞行速度快和机动性强等优势成为后续发展中具有潜力的方案［1］。

在制导模型设计方面，由于滑翔导弹弹道在干扰情况下会偏离标称，造成较大的位置、速度散布并产生额外的控制负担，所以，轨迹跟踪与能量管理建模方法引起了国内外学者的广泛研究。

在轨迹跟踪建模方面，李晓龙［2］将高度控制回路转化为经典控制理论中的二阶无静差系统，提出一种具备高度跟踪的制导模型。在此基础上，刘凯［3］应用极点配置方法，给出保证闭环稳定性的PD制导模型参数设计准则，从而完成考虑气动不确定性的轨迹纠偏，但是由于上述跟踪模型缺少速度反馈回路，所以无法在扰动情况下保证速度的一致性，存在末速散布大的问题。

在能量管理建模方面，李瑜［4-5］通过规划倾侧角-速度剖面模型构建H-V 再入走廊，结合航向误差走廊模型优化倾侧反转时机，在满足终端高度、速度约束的同时，将航向角误差控制在一定范围内。在此基础上，傅瑜［6-7］基于预测制导模型，通过在线积分得到末端状态并以迭代的方式实现控高控速的目的。但是由于上述模型全程采用基于弹道偏角误差门限的倾侧翻转逻辑进行横侧向通道轨迹控制，存在横侧向航迹不固定、位移偏差大的问题，并不适用于有着严格禁飞安全距离约束的滑翔导弹。

综上所述，考虑到现有模型在跟踪滑翔导弹航迹时，存在横侧向位移偏差大无法满足禁飞安全距离约束和末速散布大的问题。这里首先基于任务预划分手段以减小末端速度、位置散布为目的，将弹道预先划分为控速段与跟踪段。在跟踪段利用线性二次型调节器以位移加权误差最小为优化指标，完成轨迹跟踪制导模型设计。在控速段在轨迹跟踪制导律纵向通道附加空气刹车攻角修正量，结合倾侧角翻转逻辑完成能量管理模型设计。最后开展拉偏条件下的对比仿真和蒙特卡洛打靶，通过对照分析位置、末速散布方式，验证本文制导模型控制精度优于传统方案，从而为滑翔导弹轨迹跟踪方案提供潜在的技术途径。

1 动力学建模与问题描述

1.1 动力学建模

在弹道坐标系中建立动力学模型，采用倾斜转弯模式（Bank To Turn，BTT），整个再入过程均为无动力状态，在球形大地假设下给出三维动力学模型，即

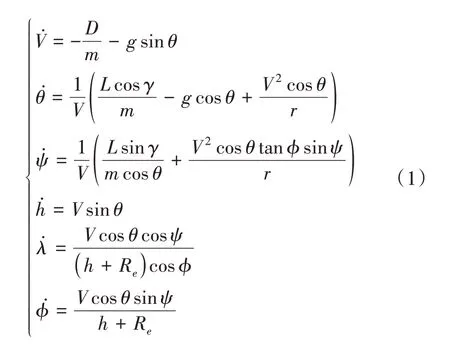
式（1）中，V是速度，θ是弹道倾角，ψ是弹道偏角，h是高度，λ是飞行器在地表投影点的经度，φ是飞行器在地表投影点的纬度，Re为地球半径，g是重力加速度，m是飞行器的质量。γ是倾侧角，D是阻力，L是升力，L和D的计算方法由式（2）给出，即

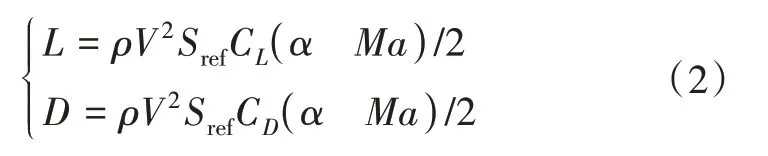
式（2）中，ρ表示大气密度，可以视为高度的函数，Sref为参考面积，CL和CD分别表示升力和阻力系数为攻角α和马赫数Ma的函数。

1.2 航迹跟踪问题描述

轨迹跟踪制导问题可以描述为，对于给定的滑翔段标称轨迹，即

其中，(t)为标称弹道状态量，为射击系z项标称位移和速度，(t)为控制量。

利用线性二次型控制器设计原理，设计如下的状态反馈控制器：

其中，(t)为控制量修正值，e(t)为状态量标称值与实际值之差。

状态反馈控制器基于设定的综合考虑制导控制偏差与偏差控制量积分的加权性能指标函数，即

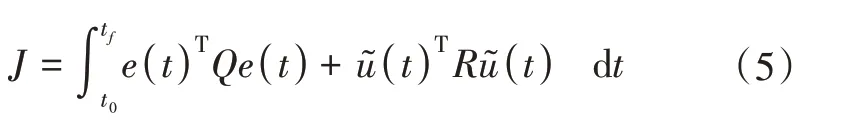
计算满足J最小的状态反馈控制器系数，使得飞行器能够用较小的加权偏差控制量确保实际飞行状态与跟踪标称飞行轨迹中装订值的总的偏差加权值最小。即

则轨迹跟踪制导问题转化为如下的状态反馈控制器参数优化设计问题：

1.3 能量管理问题描述

能量管理问题可以描述为基于事先规划的滑翔段标称轨迹，在轨迹跟踪制导律纵向通道附加空气刹车攻角修正量Δαc，在正拉偏（速度大于标称）情况下以大攻角指令形式实现降速，即

其中，KL为设定的空气刹车减速增量系数。

大攻角产生的额外升力通过设计倾侧角指令γc，以倾侧的方式确保升力纵向分量等于标称攻角产生的升力，实现高度跟踪。同时为避免倾侧产生较大横侧向位移，设置倾侧角反转逻辑，即

其中，为滑翔段标称轨迹弹道偏角。

综上，能量管理模型在正拉偏情况下以小范围牺牲横侧向精度的方式，通过空气刹车进行减速，从而消除散布，实现较高的速度，高度制导精度。

2 任务预划分手段

在得到离线规划好的弹道后，需要基于任务预划分手段预先划分为控速段与跟踪段，结合轨迹跟踪与能量管理模型实现减小末端速度、位置散布的目的。具体流程如下：

（1）读取标称弹道数据，导弹任务初始化为stageenergy=1，其中stageenergy=1 为控速段状态，0 为跟踪段状态。

（2）针对减小末速散布的需求，为提高空气刹车减速效率，基于动压Qv分配导弹任务，即

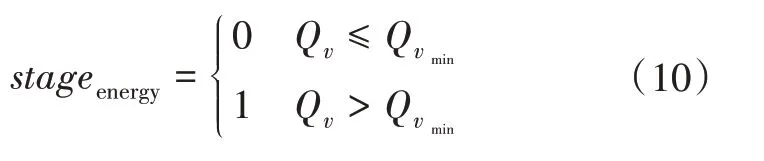
其中，Qvmin为控速段动压门限。

（3）在任务状态依旧为stageenergy=1 时，为避免在减速段因为标称倾侧角幅值过大，弹道偏角误差频繁大于误差门限导致震荡，基于再次分配任务，即

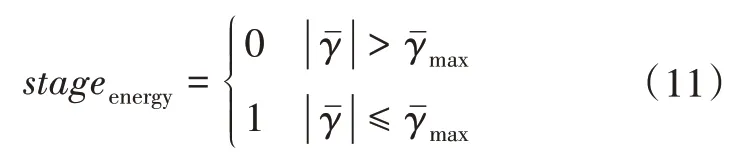
其中，为控速段倾侧角门限。

（4）在任务状态依旧为stageenergy=1时，为避免在绕飞时产生较大横侧向位移偏差，导致无法满足禁飞安全距离约束，基于导弹与禁飞区航程ΔR再次分配任务，即

其中，ΔRmax为禁飞区航程约束门限。

在依次完成步骤（1）～（4）的判断后，导弹基于当前状态分别选择相应模型进行制导指令解算，如图1所示。

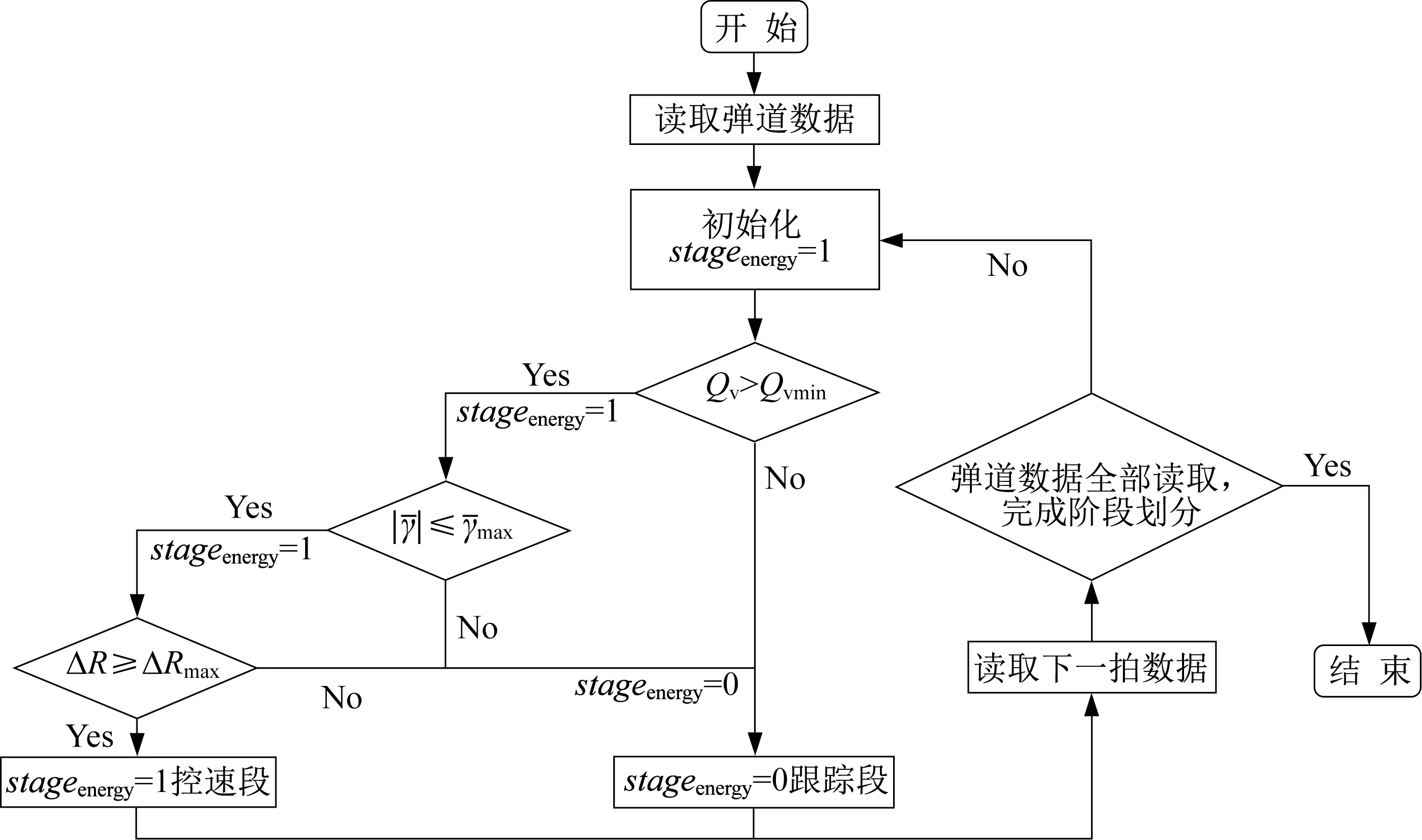
图1 任务预划分手段流程图Fig.1 Flow chart of task pre-division means

3 轨迹跟踪模型

将高度h、射击系Z项位移影响作为关注状态量，引入位移微分项对状态方程扩维，沿飞行轨迹线性化可得

描述为状态空间形式为

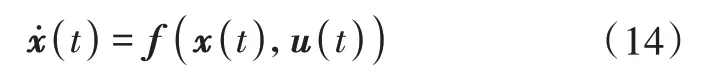
考虑飞行过程中与标称轨迹的偏差，沿着e(t)=0，(t)=0进行线性化可以得到

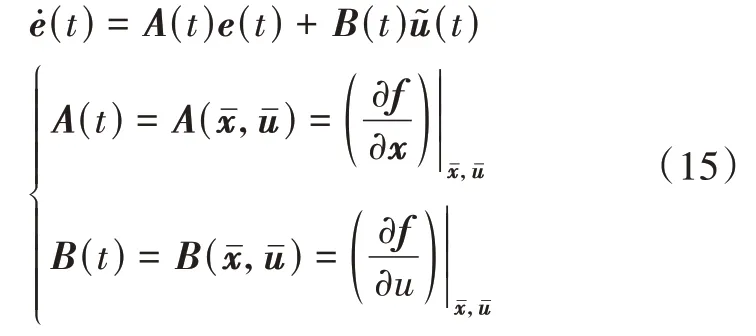
针对线性化后的时变系统，这里需要设计一个状态反馈控制器，即

通过线性二次型调节器配置反馈矩阵K，找到一组控制量u(t)。假设存在一个常量矩阵P使得

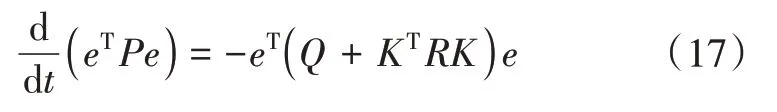
代入J后

令K=R-1BTP，则

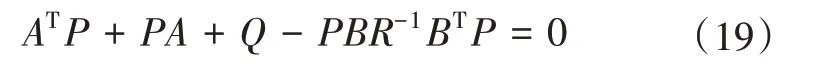
在此基础上，通过求解黎卡提方程得到矩阵P与控制参数K，轨迹跟踪模型可以表示为

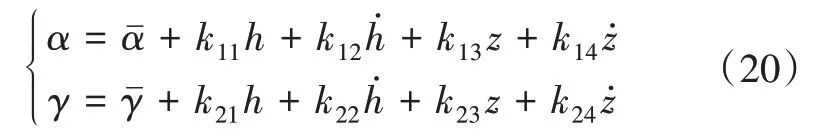
4 能量管理模型

在导弹处于控速阶段，在轨迹跟踪制导律纵向通道附加空气刹车攻角修正量Δαc，以设定的大攻角指令αc实现降速，即

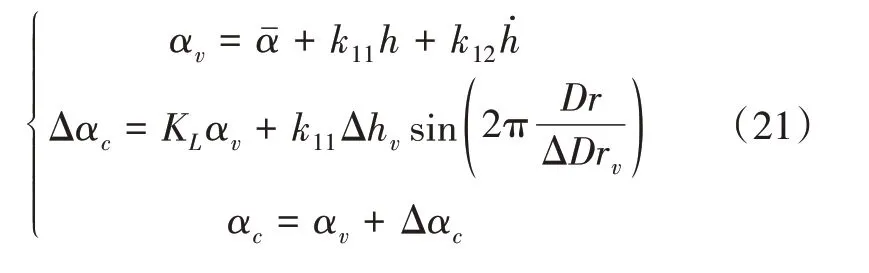
其中，αv为确保导弹在纵向通道稳定跟踪的指令攻角，Δhv为设置的高度小量，ΔDrv为设置的航程小量。

大攻角产生的额外升力通过设计倾侧角指令γc，以倾侧的方式确保升力纵向分量等于标称攻角产生的升力，实现高度跟踪。在无法在线使用气动库的情况下，需要提前拟合升力系数，从而完成倾侧角指令设计。

由式（2）可知，在已知马赫数的情况下，升力系数与攻角相关，可基于最小二乘法将不同马赫数下的升力系数拟合成以攻角为自变量的函数，即

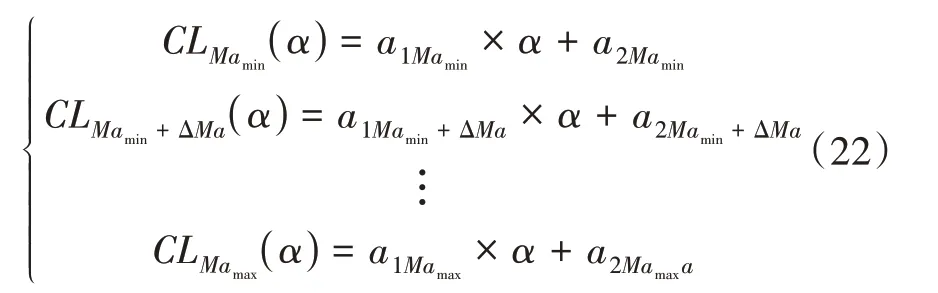
其中，ΔMa为气动库中马赫数各节点之间的步长。

在此基础上，再次利用最小二乘法将各个节点的参数拟合为以马赫数为自变量的函数，则线性回归模型为

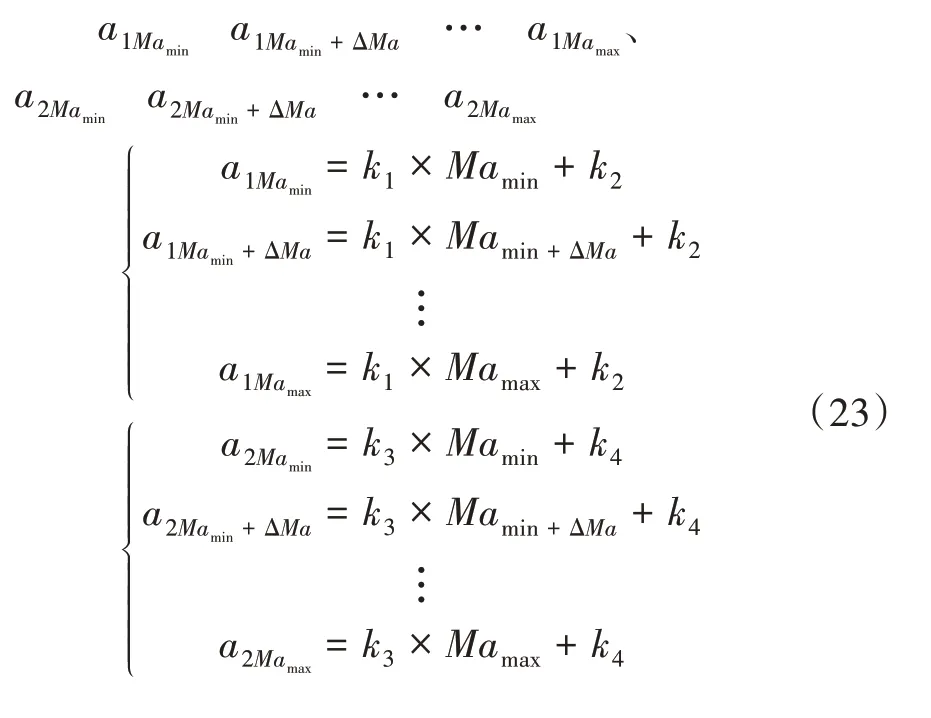
写成矩阵形式为

采用最小二乘法对未知参数估计，即求解k的估计值

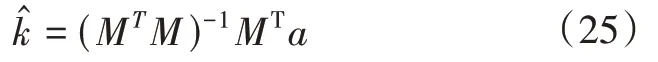
完成对升力系数的拟合，即

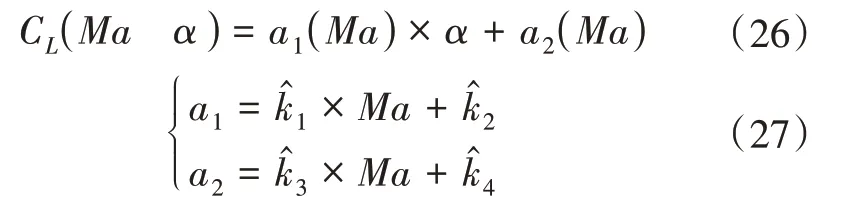
基于升力系数拟合函数，保证升力纵向分量等于标称攻角所产生的升力倾侧角指令，可以为以下形式：

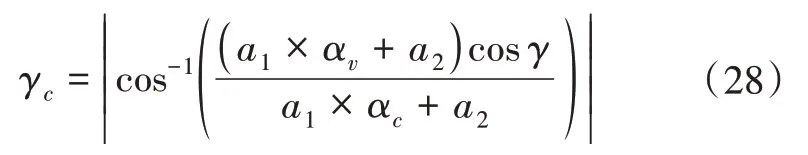
当倾侧角指令超出范围（γc≥γcmax）后指令限幅，为避免限幅后升力纵向分量大于标称攻角所产生的升力，从而无法进行高度跟踪。这里需要减小空气刹车攻角，则

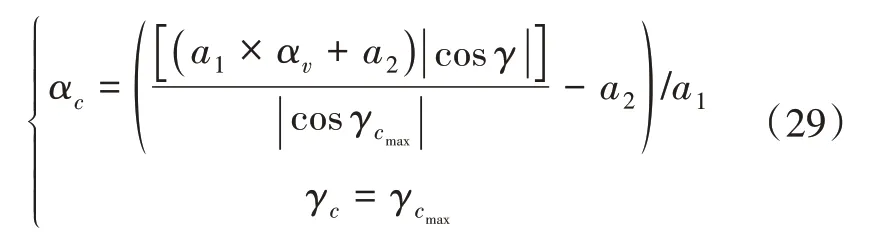
在此基础上，为避免倾侧产生较大横侧向位移，需要设置倾侧角反转逻辑。当弹道偏角误差大于误差门限Δψfz时，改变倾侧角符号，当弹道偏角误差小于门限时，保持倾侧角符号不变。

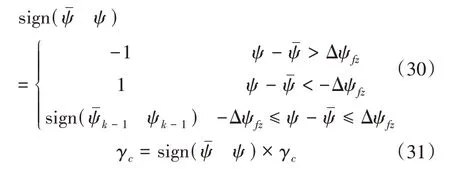
式（31）中，k- 1表示上一拍。

5 仿真分析

5.1 仿真输入

假设导弹发射点经纬度为（0.0°，0.0°），计划绕过经纬度为（-8.5°，1.4°）、（-6.5°，0.9°）的两个40 km半径禁飞区，并到达距离经纬度为（11.6°，1.8°）的目标点。这里导弹初始弹道倾角为85.0°，弹道偏角为0.0°，以末速最大为指标，优化得到图2中的攻角、倾侧角剖面，并积分得到图3中满足禁飞约束的离线规划标称弹道。

图2 标称攻角、倾侧角-航程曲线Fig.2 Curves of nominal attack angle VS range and pitch angle VS range

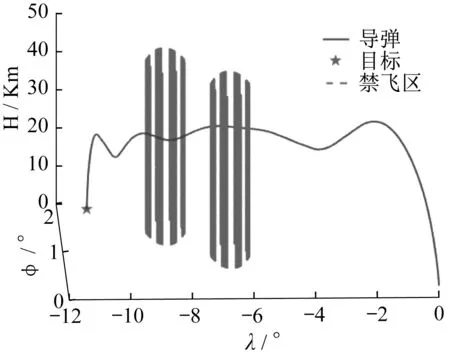
图3 导弹轨迹图Fig.3 Trajectory graph of missile

在此基础上，结合图2的攻角、倾侧角剖面，这里兼顾禁飞区绕飞阶段的横侧向制导精度需求与控速需求，基于任务预划分手段以航程为自变量，将弹道滑翔段提前分为三段，分别是50~250 km 的轨迹跟踪段、250~600 km的能量管理控速段和600~1100 km的轨迹跟踪段，实现分段航迹纠偏与控速。

5.2 轨迹跟踪与能量管理仿真分析

本小节考虑气动、推力不确定性的轨迹跟踪仿真分析，通过与传统算法对比末速散布ΔVf与最大、终端位置偏差(ΔHmaxΔZmax)、(ΔHfΔZf)的方式，验证建立的模型是否具有稳定跟踪标称弹道并减小末速散布的能力。

图4为标称状态与拉偏状态下进行能量管理的攻角、倾侧角对照曲线。其中，轨迹跟踪与能量管理模型在航程为50~250 km、600~1100 km 的跟踪段，基于当前时刻的位置、速度偏差解算修正指令，通过在标称值上附加攻角与倾侧角的方式确保跟踪误差不发散；在250~600 km 的控速段，通过纵向通道附加空气刹车攻角修正量并多次反转倾侧角的方式，在小范围牺牲横侧向精度的情况下实现控高控速的目的。

图4 攻角、倾侧角-航程曲线Fig.4 Curves of attack angle VS range and pitch angle VS range

图5-7 为基于表1拉偏条件，分析能量正向拉偏弹道仿真的速度和位置误差-时间曲线。图5中分别为标称状态、采用轨迹跟踪与能量管理模型和传统P/D 跟踪模型的速度-时间曲线。在标称状态末速Vf为668 m/s 的情况下，轨迹跟踪与能量管理模型在保证跟踪误差不发散的同时，通过空气刹车的方式有效降低了散布。最大末速偏差由P/D 制导的328 m/s 降为180 m/s，速度一致性得到大幅提升。

表1 拉偏信息表Tab.1 Pull deviation information table

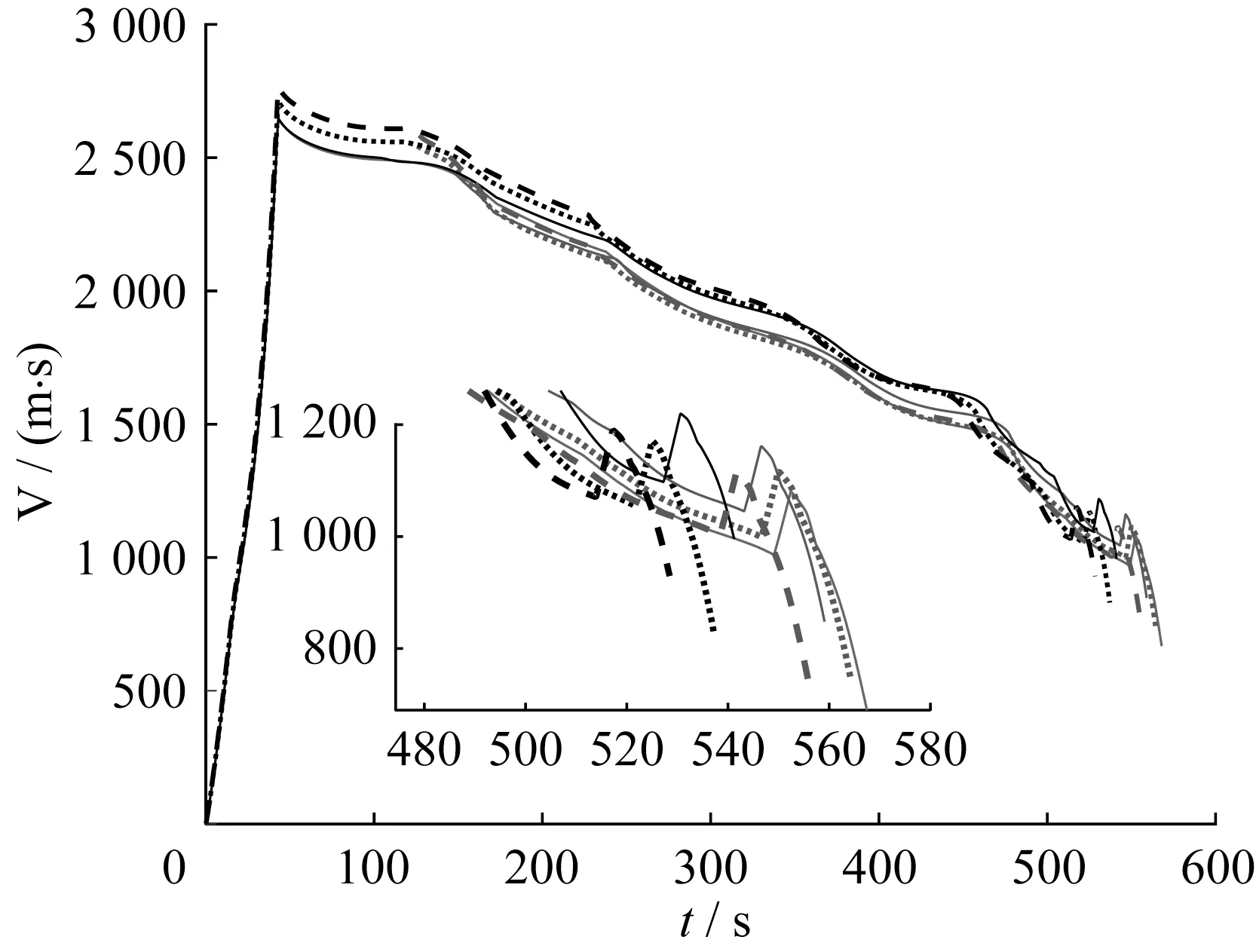
图5 速度-时间曲线Fig.5 Curve of speed VS time

图6-7 中分别为使用轨迹跟踪与能量管理模型和传统P/D 跟踪模型的高度、横向位移误差-时间曲线。结合表3可知，由于本文方法在控速段以小范围牺牲横侧向精度的方式进行空气刹车减速，所以在控速段产生了一定的横侧向位移，导致误差最大值（1030 m）大于传统P/D 控制（284 m）。但是如图8所示，控速模型设置了最大弹道偏角偏差，当控速段实际弹道偏角误差大于误差门限时改变倾侧角符号，从而通过翻转避免产生较大横侧向位移并导致误差发散。

图6 高度误差-时间曲线Fig.6 Curve of height error VS time

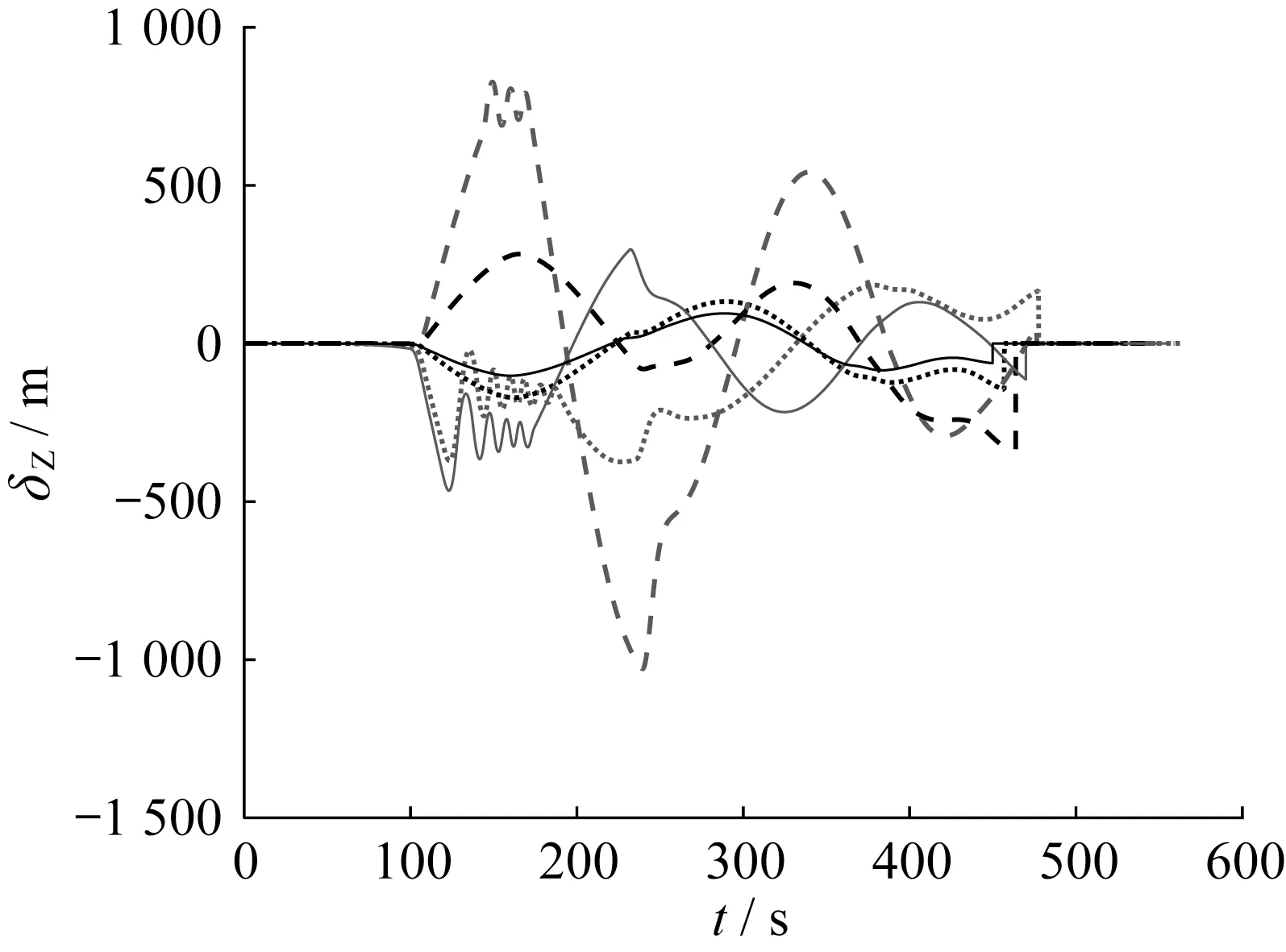
图7 Z项位置误差-时间曲线Fig.7 Curve of position error of Z axis VS time

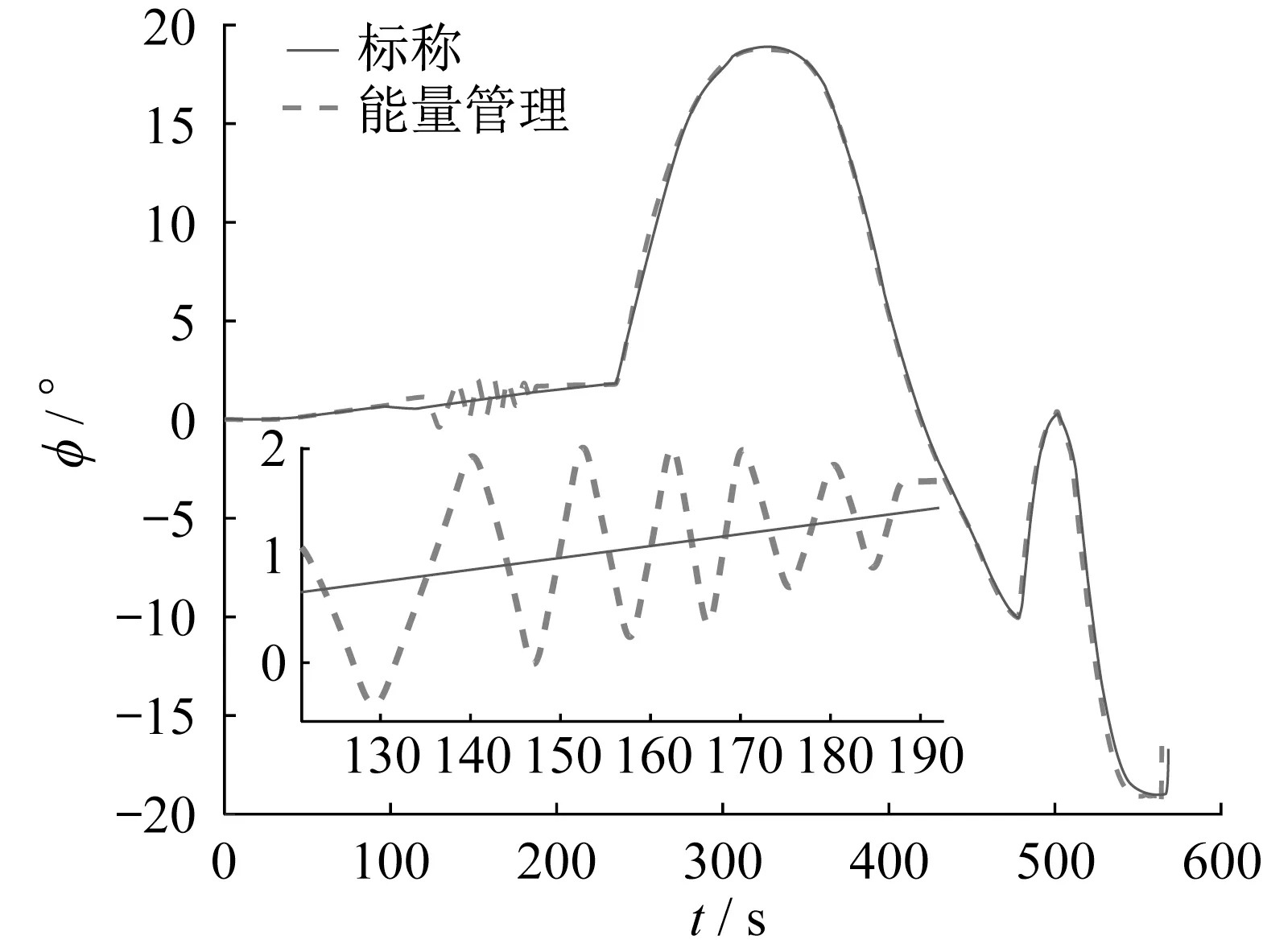
图8 弹道偏角-时间曲线Fig.8 Curve of deflection angle VS time

表2 拉偏数据对比表Tab.2 Comparisons of simulation results

表3 位置偏差对比表（最大值）Tab.3 Comparison of the maximum position error

结合表4，通过与P/D 控制对比终端位置偏差可知，两者控制误差不明显。因为本文方法在600~1100 km 的跟踪段重新引入轨迹纠偏模型，所以能够在控速段引入了较大的位置偏差后快速进行轨迹纠偏，使得跟踪误差收敛。

表4 位置偏差对比表（终端）Tab.4 Comparison of terminal position error

5.3 蒙特卡洛仿真分析

本小节开展气动、推力偏差和大风组合干扰情况下的蒙特卡洛打靶仿真，以概率分析的方式对比轨迹跟踪与能量管理模型与P/D 模型的末速散布及位置偏差，如图9-11，验证本文模型制导控制精度是否优于传统方案。

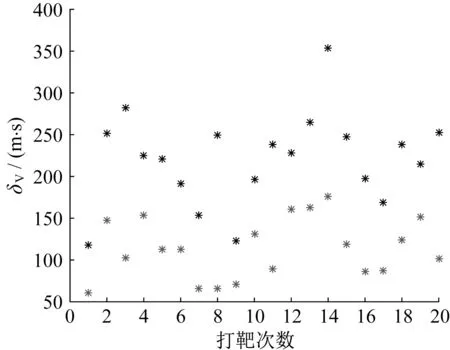
图9 ΔVf蒙特卡洛打靶Fig.9 Monte Carlo shooting of ΔVf

由图9可知，在20次的蒙特卡洛打靶仿真中，轨迹跟踪与能量管理模型ΔVf全部小于200 m/s，60%概率ΔVf小于100 m/s；而P/D 模型只有35%概率ΔVf在200 m/s以内。

由图10-11 可知，2 种模型ΔHmax、ΔZmax全部在2 km 以内，轨迹跟踪+能量管理模型有95%概率在1 km，而P/D 模型为100%；ΔHf、ΔZf在1 km 以内概率均为100%。

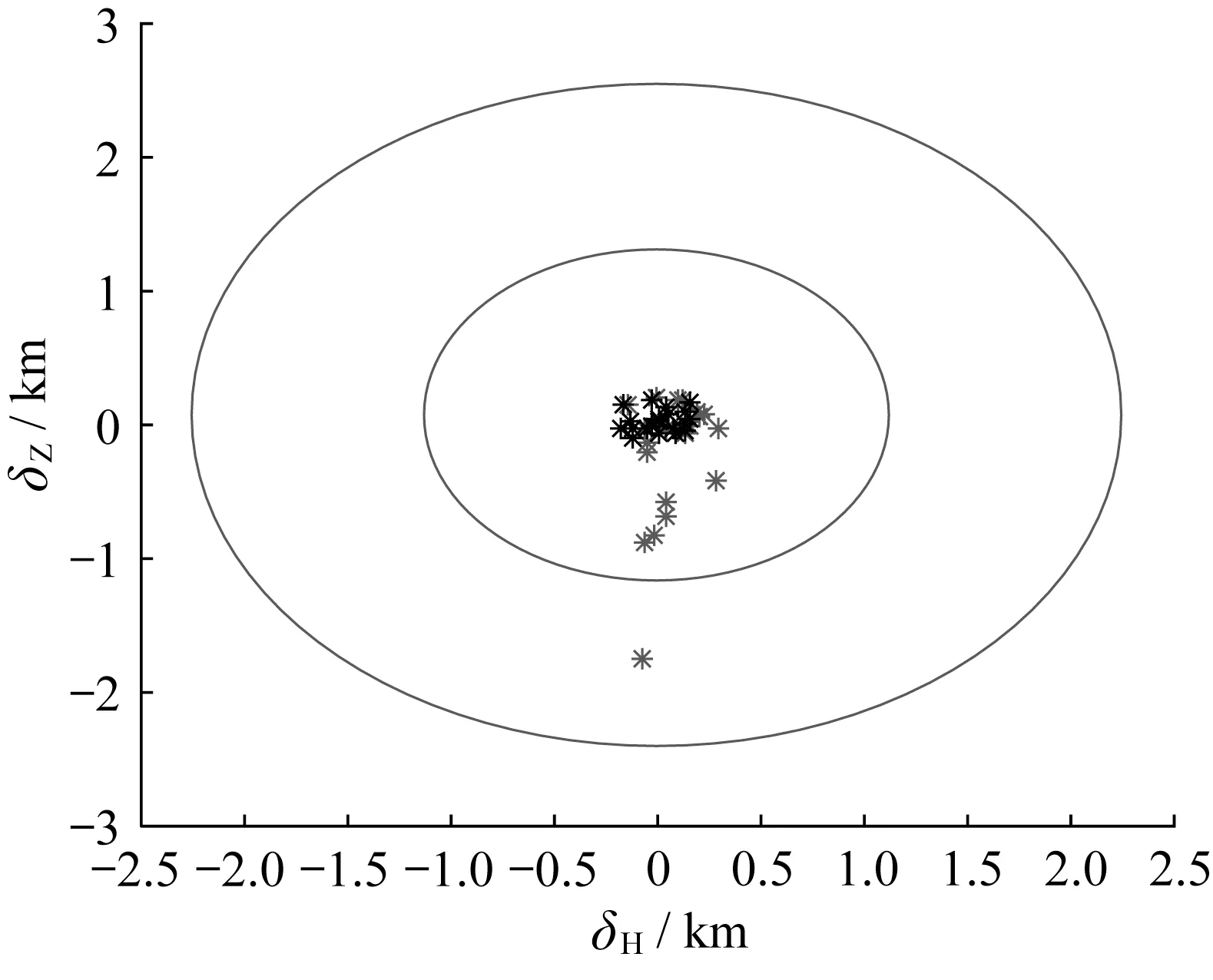
图10 ΔZmax-ΔHmax蒙特卡洛打靶Fig.10 Monte Carlo shooting of ΔZmax VS ΔHmax

图11 ΔZf-ΔHf蒙特卡洛打靶Fig.11 Monte Carlo shooting of ΔZf VS ΔHf

综合6.2和6.3小节拉偏情况下的数学仿真可知，2 种模型的终端位置偏差相似，但轨迹跟踪+能量管理模型具有更小的末速散布，从而避免产生额外的控制负担。

6 结 论

本文针对干扰情况下弹道偏离标称，造成较大的位置、速度散布并产生额外的控制负担的问题。首先基于任务预划分手段以减小末端速度、位置散布为目的，将弹道预先划分为控速段与跟踪段。在此基础上，各段分别建立轨迹跟踪模型和空气刹车+倾侧角反转逻辑模型，实现考虑不确定条件的分段在线纠偏与控速。最后开展蒙特卡洛打靶对比仿真，通过对照分析最大、终端位置偏差和末速散布的方式，验证了本文模型制导控制精度优于传统方案，从而为滑翔导弹轨迹跟踪方案提供潜在的技术途径。