基于平面电容传感器阵列的动态手势识别技术

王子懿, 沈三民, 佘硕铖

(中北大学 仪器科学与动态测试教育部重点实验室, 山西 太原 030051)

0 引 言

随着计算机技术的发展, 智能机器和虚拟现实等相关技术也得到了极大的发展, 因此, 人机交互便成了近年来被广泛研究的热点之一[1]。 基于动态手势识别的人机交互也逐渐受到各个领域的青睐。

动态手势识别是指对人手部运动轨迹进行识别, 关注某一段时间的连续动作, 更加符合人的表达习惯, 而与其对应的静态手势识别只是关注某时刻的手部外形特征。1996年,Kadous等[2]利用PowerGlov设备, 运用实例学习和决策树判别的方法对95个手势识别, 识别率为80%; 哈尔滨工业大学的吴江琴等[3]利用美国Vinual Technologies公司的CyberGlove型数据手套, 将人工神经网络与隐马尔可夫模型(HMM)相结合, 成功建立了120个简单手语词的手语识别系统。 虽然基于可穿戴设备的手势识别可以准确获得手势信号,但由于穿戴设备不够方便且降低了手指的灵活性,基于视觉与感应传感器的非接触手势识别应运而生。1997年,Grobel等采用HMM 对手部图像进行处理, 手势识别率达95%;2011年,Kurita教授分析了人体静电分布情况, 并利用静电感应信号实现了对双足机器人的控制[4]。2006年,Wimmer等利用平面电容传感器识别动态手势, 实现了非触的屏幕控制[5]。 目前, 利用视觉的手势识别技术受光线影响较大, 而基于感应传感器的主要的3种方式中, 激光与静电方式受光线与气候的影响较大, 电容检测方式较前两种受环境影响较小, 并且现行的电容检测方式主要实现了简单的位置解算。

本文将使用卡尔曼滤波与基于视觉手势识别的HMM 方法[6], 实现对平面电容传感阵列的信号捕捉与手部运动轨迹提取, 并完成简单图形的识别。

1 平面电容传感阵列识别机理

1.1 平面电容传感器的电场分布

电容传感器的激励电极与感应电极通常情况下呈平行对立放置, 所以, 两电极间的电场线也在两极板之间平行均匀分布。 当两个电极慢慢张开, 传感器内部原本均匀平行的电场线逐渐向外扩张, 直至两极板完全打开至共面状态时, 两极板之间的边缘电场占主要地位, 而内部电场却十分微弱, 如图1所示。 平面电容传感器阵列正是利用这一效应识别敏感区域内的动态手势[7]。

图1 平行板电容旋转为平面电容Fig.1 Parallel plate capacitance rotation to a flat capacitor

人体脂肪的相对介电常数约为12.7, 肌肉的相对介电常数约为66.2, 均大于空气的介电常数。因此, 当人体靠近平面电容传感器时, 传感器敏感空间内介质的介电常数会发生改变, 传感器容值也会相应改变。

1.2 平面电容传感器阵列的动态手势识别原理

基于平面电容传感器阵列的动态手势识别流程如图2所示。 首先, 由平面电容传感器阵列感应手部运动, 电容检测系统采集感应数据[ΔCij]n×m, 不同时刻的手部空间位置的变化即是手部运动轨迹。 由于环境噪声等因素造成手部运动轨迹的平滑度低, 因此, 采用卡尔曼滤波对手部运动轨迹进行降噪处理为(x,y)[8]。 利用手部位置跟踪HMM 算法解算出某时刻对应的手部的空间位置(Xs,Ys), 并匹配预先设置的动态手势识别图形Gi, 最后, 通过上位机根据识别的图形进行相应的交互操作。

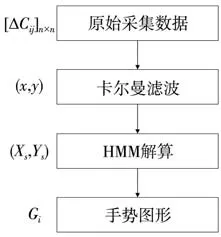
图2 基于平面电容传感阵列的动态手势识别过程Fig.2 Dynamic gesture identification process based onflat capacitive sensing array

2 电容传感器阵列结构设计

平面电容传感器激励电极与感应电极结构与位置的不同, 将影响该传感器的电容分布。 其中,主要的电极形状有圆形, 矩形, 梳齿形, 螺旋形等[9-10]。 各种形状的传感器在COMSOL软件中得出的网格划分图如图3所示。

图3 4种形状传感器的尺寸与网格Fig.3 Size and grid of four shape sensors

使用COMSOL软件仿真获得的4种形状电极的三维电场图与电势图如表1所示。 由表1中的三维电场图可以看出, 敏感空间主要分布于电极间隙。 对于圆形与矩形电极而言, 该区域相对整个电极平面来说面积较窄; 对于梳齿形与螺旋形电极而言, 电极间面积相对较大且分布相对均匀, 且由于梳齿形及螺旋形电极的电极相互感应部分较多, 在相同电极大小的情况下, 这两种形状的电极电场模较大[11]。 经过仿真与理论分析可知, 螺旋形电极敏感空间较大且较为均匀。 因此, 本文采用螺旋形电极进行平面电容传感阵列的设计。

表1 4种形状电极的电场图与电势图Tab.1 Electric field map and potential map of four shape electrodes

通过对比表1中的仿真结果, 最终确定了单个电极的形状采用螺旋形结构, 由于采用蜂窝形结构可以在同样的传感面积内加入更多的传感单元, 故本文设计的传感器阵列采用六边形结构,共19个电极单元, 如图4所示。 在电极平面中,通过六边形结构将每个电极单元包裹起来形成屏蔽电极地, 这样设计可以有效减少相邻电极单元之间的串扰, 并且六边形的设计可以在相同的空间内堆积更多的电极单元(平面最密堆积)[12], 增加手势识别的精确度。 电极宽度、 电极长度、 电极厚度、 基板的厚度、 基板的介电常数等均通过仿真方法进行确定[13]。 经过仿真与实验验证, 最终设计出来的基于平面电容传感器阵列的尺寸如下:交互界面的面积约为460 mm×540 mm, 屏蔽地宽度为10 mm, 单个传感器半径约为80 mm, 其电宽度与极间距均为5 mm。

图4 平面电容传感器阵列结构图示Fig.4 Structure illustration of planar capacitance sensor array

如图4所示, 传感器正面为电极单元和屏蔽地的铜层组成, 并在底面添加衬底与保护电极,其中衬底为绝缘衬底, 保护电极是在平面电容传感器的衬底背面覆盖导体并接地, 这样可以一定程度地减少环境产生的寄生效应, 从而减小杂散电容, 减小噪声的干扰[14]。

3 手部位置跟踪算法

当手部处于传感器阵列敏感区域时, 会与各个电极形成多电容, 但每个位置的感应强度有所不同, 手部距离越近的传感器感应越强。 因此, 可以根据不同传感器感应的大小(检测系统的输出电压变化大小)引入线性加权法来估计手部的空间位置。 其计算式如下

式中:ΔVi为电容检测系统各通道的电压变化值,(xi,yi)为平面电容传感器阵列中每个传感器的电极质心坐标。 当手部从远处移动到传感器阵列的感应区域时, 手部处于某传感器的电极正前方,此时手部与该传感器的电极距离最近, 电容检测系统对应的检测通道输出电压变化值最大, 因此,其在坐标计算时权重最大。 本文通过设定电压阈值点来判断手势运动的开始点和结束点, 即当传感器阵列中任意传感器的信号输出超过阈值, 则认为手部运动开始, 当传感器阵列中所有传感器的信号输出均不超过阈值, 则认为手部运动结束。图5为根据式(1)计算得到的坐标绘制的手部运动轨迹。 两次试验的手部运动轨迹都为“V”形, 从图中可以看出, 经过新的手部运动轨迹跟踪方法得到的轨迹曲线平滑度差, 会大大降低对轨迹图形的识别效率, 因此, 需要对轨迹曲线进行平滑处理。 本文选择的卡尔曼滤波方法动态手势识别中被广泛应用。

图5 根据手部位置跟踪方法得到“V”形轨迹Fig.5“V”trajectory according to the hand positiontracking method

本文通过卡尔曼滤波算法对手部运动轨迹在MATLAB软件上进行仿真[15]。 仿真时, 在真实的手部运动轨迹上叠加10%的白噪声, 使用卡尔曼滤波后得到的手部运动轨迹如图6所示。 从图中可以看出, 经过手部位置跟踪算法解算后的手部运动轨迹散布在真实轨迹周围, 经过卡尔曼滤波后, 手部运动轨迹变得平滑且接近于真实轨迹。

图6 卡尔曼滤波算法仿真结果Fig.6 Kalman filter algorithm simulation results

手势识别的实质是曲线识别和匹配。 曲线识别和匹配中, 常用链码(又称为freeman 码)描述曲线, 链码匹配算法描述链状结构时具有显著优越性, 因此被广泛应用于曲线、 图形的模式识别等领域[16]。 本文采用的平面电容传感器的电极数较少, 因此无需采用过多方向链码, 选用8方向链码即可对手部运动轨迹每个时段的运动方向进行离散化(如图7所示), 由该图可见,8方向在二维空间内均匀分布。 如果采用8方向链码编码表示图8所示的运动曲线, 则曲线的编码为8822。 通过上述的链码对曲线编码, 其编码值构成特征向量, 即得到特征观察量O={O1, …,Ok}, 再利用HMM 识别算法对手部运动轨迹进行识别[17]。

图7 空间运动8方向链码图示Fig.7 Space motion 8 direction chain code illustration

图8 待编码的运动曲线Fig.8 Sport curve to be encoded

HMM 识别算法主要通过观测出的坐标结果来预测本次手势内容, 该模型主要包含观测量O,隐含状态S; 参数矩阵包含初始状态分布矩阵π,状态转移概率矩阵A及观测状态概率矩阵B。 首先需要使用EM 算法中的鲍姆-韦尔奇算法(Baum-Welch algorithm)对不同手势的矩阵模型(π,A,B)进行训练, 然后通过向前向后算法求出当前观测序列在不同模型下出现的概率, 同时设定一个概率阈值, 若出现概率均没有超过设定的概率阈值, 则认为此次手势识别失败, 否则, 出现概率最大的模型即为当前手势识别结果。

4 图形设计与试验验证

本文主要实现0～5数字的文字识别, 预设的交互图形见图9。 由于0～5中有些数字形状较为复杂, 为了提高图形识别率, 本文对其进行了简化处理。 利用简化处理后的交互图形, 可以降低识别的难度。 数字图形的简化与原图形基本类似,仍能从简化图形中直观看出对应的数字, 这样不会降低用户体验。

图9 预设的数字图形与文件操作图形Fig.9 Preset digital graphics and file operation graphics

在进行动态手势识别图形试验时, 对于HMM 模型的训练样本数为50, 人手距离电极平面约为200 m。 每种图形的测试数为25。 根据每次试验中正确次数计算出成功识别图形的正确率。从表2可以看出, 数字“1”这类较为简单的图形状识别率最高为100%, 其余数字图形的识别率均在88%以上, 平均识别率达到95%。

表2 动态手势识别结果Tab.2 The result of dynamic gesture identification

在通过对各个数字进行识别后发现, 较为简单且直观的数字识别率较高, 如果图形较为复杂, 则识别率会相应降低。 因此, 在基于手势识别进行人机交互的命令设计时, 可以设置一些较为简单的图形, 其一方面可以相应的提升传感器的识别率, 另一方面也可以降低使用难度, 提高用户的体验感。

5 结束语

本文利用平面电容传感器对人体的敏感性,开展了基于平面电容传感阵列的动态手势识别应用研究。 使用手部位置跟踪算法得到了手部运动轨迹曲线, 再利用卡尔曼滤波算法对手部离散位置进行预测和平滑处理, 显著提高了噪声条件下手部运动轨迹的位置解算精度。 并运用HMM 算法对手势轨迹进行识别, 实现了对预设交互图形的匹配。 最后, 通过实验验证了该系统对数字图形0～5的识别, 平均识别率高达95%, 可以较好地运用于基于动态手势识别的简单的人机交互。