纯反馈系统的自抗扰预设定有限时间量化控制

吴思涵，李小华*，张立鹏，赵洪利

(1.辽宁科技大学 电子与信息工程学院，辽宁 鞍山 114051;2.辽宁科技大学 图书馆，辽宁 鞍山 114051)

在实际生产和生活中，存在大量非线性系统，其中很多可用纯反馈模型描述，如柔性关节机械臂系统[1-2]和化学反应系统[3]等.这些系统可采用网络控制，但网络控制存在丢包和带宽限制等问题，故要量化处理控制信号[4-5]、降低信号传输频率，以防止信号在传输中丢失、保证系统的控制性能.

在工业控制中，PID(proportional integral derivative)控制仍然占据主导地位.为了提升PID的控制效果，文献[6]提出了一种自抗扰控制方法.与自抗扰控制有关的研究分为2大类：一类是直接设计系统的自抗扰控制器，并应用于实际系统[7-9]；另一类是基于反步法控制将扩张状态观测器(extended state observer，简称ESO)、跟踪微分器(tacking differentiator，简称TD)分别用于估计未知项、虚拟控制函数的导数，以避免出现微分爆炸现象[10-12].

文献[13]提出预设性能控制，该控制能使系统的跟踪误差满足预先设定的动态和稳态性能要求.由于预设性能控制能同时保证系统动态性能和稳态性能，因而已成研究热点[14-16].

有限时间控制分为：精确有限时间控制[17-18]和实际有限时间控制[19-22].精确有限时间控制能使被控制的量在有限时间内收敛至平衡点，而实际有限时间控制仅在有限时间内收敛至平衡点附近的小邻域，且没有考虑暂态过程.文献[22]将预设性能控制与有限时间控制相结合，提出了一个预设有限时间性能函数，能同时进行暂态性能控制和有限时间控制，且此类有限时间控制的停息时间是设计参数，与系统初始状态无关.

自抗扰控制能改善系统的抗扰性能，预设有限时间控制能同时改善系统的暂态和稳态性能，因此该文将二者结合起来，针对一类具有量化输入的非仿射纯反馈系统，提出一种自抗扰预设定有限时间量化控制策略.

1 系统控制问题的描述

该文考虑的非仿射纯反馈非线性系统为

(1)

(2)

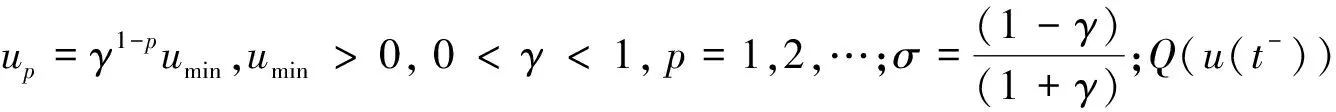
从(2)式可看出，Q(u)∈{0,±up,±up(1+σ),p=1,2,…}.由文献[23]可知

Q(u)=J(u)u(t)+L(t)，

(3)

其中：J(u)为u的未知函数，满足1-σ≤J(u)≤1+σ;L(t)为t的未知函数，满足|L(t)|≤umin.

该文基于反步法设计系统(1)的自抗扰预设定有限时间量化控制器，使跟踪误差满足预设定有限时间控制要求的动态和稳态性能，系统有界稳定，且具有抗干扰性.

这里给出对系统(1)的假设：

假设2[10]系统中的所有状态均是可测量的.

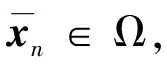
注1假设2是引入扩张状态观测器的前提.假设4，5可保证系统(1)的可控性，且与系统模型处理有关.

该文采用文献[22]中的预设定有限时间性能函数，即

(4)

其中：ρ(t)为一个光滑函数，且满足：

(1)ρ(t)>0;

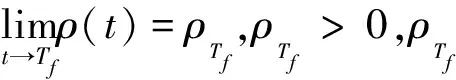
为了处理未知项和避免出现微分爆炸现象，使用文献[24]中的ESO和TD.

2 自抗扰预设定有限时间量化控制器的设计

根据文献[10]中对非仿射非线性系统的处理方法，将系统(1)转换为

(5)

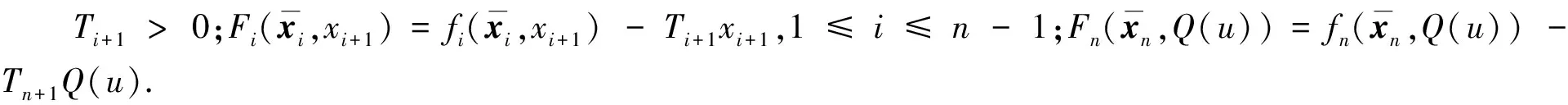
设计过程中使用的坐标变换为

e1=x1-yd，e2=x2-α1，…，en=xn-αn-1.

(6)

设

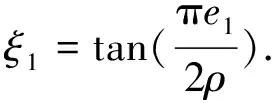
(7)

采用Backstepping方法设计自抗扰预设定有限时间量化控制器，具体步骤如下：

第1步 选取Lyapunov函数为

(8)

由式(6)～(8)，可得

(9)

其中

(10)

根据文献[24]构建ESO对F1进行估计，此ESO的方程为

(11)

其中：E1为估计误差；Z12为F1的估计值；β11，β12为设计参数.

定义式(11)的ESO估计误差为

ε1=F1-Z12.

(12)

由式(9)，(12)，可得

(13)

选取第1步的虚拟控制为

(14)

其中：设计参数c1>0.根据式(13)，(14)和Young’s不等式，有

(15)

第2步 选取Lyapunov函数为

(16)

根据式(6)，(15)，可得

(17)

构建ESO对F2进行估计，此ESO的方程为

(18)

定义式(18)的ESO估计误差为

ε2=F2-Z22.

(19)

(20)

定义式(20)的TD估计误差为

(21)

根据式(17)，(21)，可得

(22)

选取第2步的虚拟控制为

(23)

其中：设计参数c2>1.结合式(22)，(23)及Young’s不等式，可得

(24)

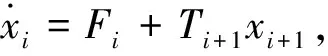
(25)

经相关计算，得

(26)

构建ESO对Fi进行估计，此ESO的方程为

(27)

定义式(27)的ESO估计误差为

εi=Fi-Zi2.

(28)

(29)

定义式(29)的TD估计误差为

(30)

选取第i步的虚拟控制为

(31)

其中：设计参数ci>1.根据式(26)，(28)，(30)，(31)，可得

ei(Zi2+εi+Ti+1ei+1+Ti+1αi-vi-1,2-ηi-1)=

(32)

(33)

经相关计算，得

(34)

构建ESO对Fn进行估计，此ESO的方程为

(35)

定义(35)式的ESO估计误差为

εn=Fn-Zn2.

(36)

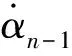
(37)

定义式(37)的TD估计误差为

(38)

根据式(34)，(38)，可得

(39)

将式(3)代入式(39)，可得

en{Zn2+εn+Tn+1[J(u)u(t)+L(t)]-vn-1,2-ηn-1}.

(40)

根据1-σ≤J(u)≤1+σ，|L(t)|≤umin和式(40)，可得

en{Zn2+εn+Tn+1J(u)u(t)+Tn+1umin-vn-1,2-ηn-1}≤

en{Zn2+εn+Tn+1(1+σ)u(t)+Tn+1umin-vn-1,2-ηn-1}.

(41)

选取量化控制输入为

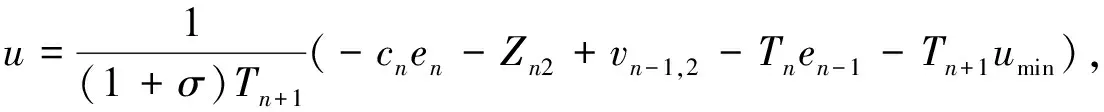
(42)

其中：设计参数cn>1.将式(42)代入式(41)，可得

(43)

基于上面的设计，可给出如下结果：

定理1对于满足假设1～5的系统(1)，且|e1(0)|<|ρ(0)|，若采用式(14)，(23)，(31)，(42)设计跟踪控制器，则受控系统具有有界性，e1(t)能被ρ(t)约束，且在设定时间Tf内收敛至期望的稳态精度(-ρTf,ρTf).

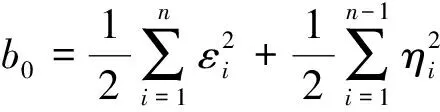
为了证明该文所提策略具有更好的抗干扰性能，将该文策略的控制效果与神经网络策略的控制效果进行对比.因为神经网络策略的证明过程与定理1类似及篇幅所限，这里仅给出神经网络控制器的设计结果，即下面的定理2.

定理2对于满足假设1～5的系统(1)，且|e1(0)|<|ρ(0)|，若选取神经网络虚拟控制律为

(44)

(45)

(46)

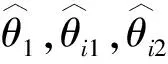
量化控制律为

(47)

自适应律为

(48)

(49)

(50)

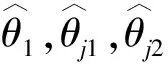
则系统(1)是有界的，且跟踪误差能满足预先设定的有限时间控制性能.

3 仿真研究

考虑如下系统

(51)

选取系统初始状态为：[x1(0),x2(0)]=[0.5,0.5];选取期望信号为：yd=sin3t;选取系统参数为：T2=T3=2;选取控制参数为：c1=c2=50;选取有限时间性能参数为：ρ0=0.8，Tf=2，ρTf=0.02;选取量化器参数为：umin=0.9，γ=0.17;选取扩张状态观测器参数为：β11=20，β12=30，β11=12，β12=22;选取跟踪微分器参数为：λ=10，δ=0.5.

该文的自抗扰预设定有限时间量化控制策略的仿真结果如图1～5所示.由图1，2可知，输出状态曲线与期望信号曲线在设定的2 s内已高度重合，跟踪误差已收敛至预先设定的(-0.02,0.02).由图3～5可知，状态x2、控制输入u及量化输入Q(u)均是有界的.

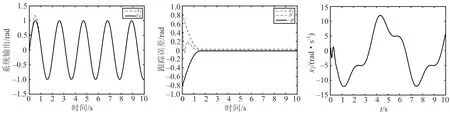
图1 输出状态跟踪效果 图2 跟踪误差 图3 状态x2

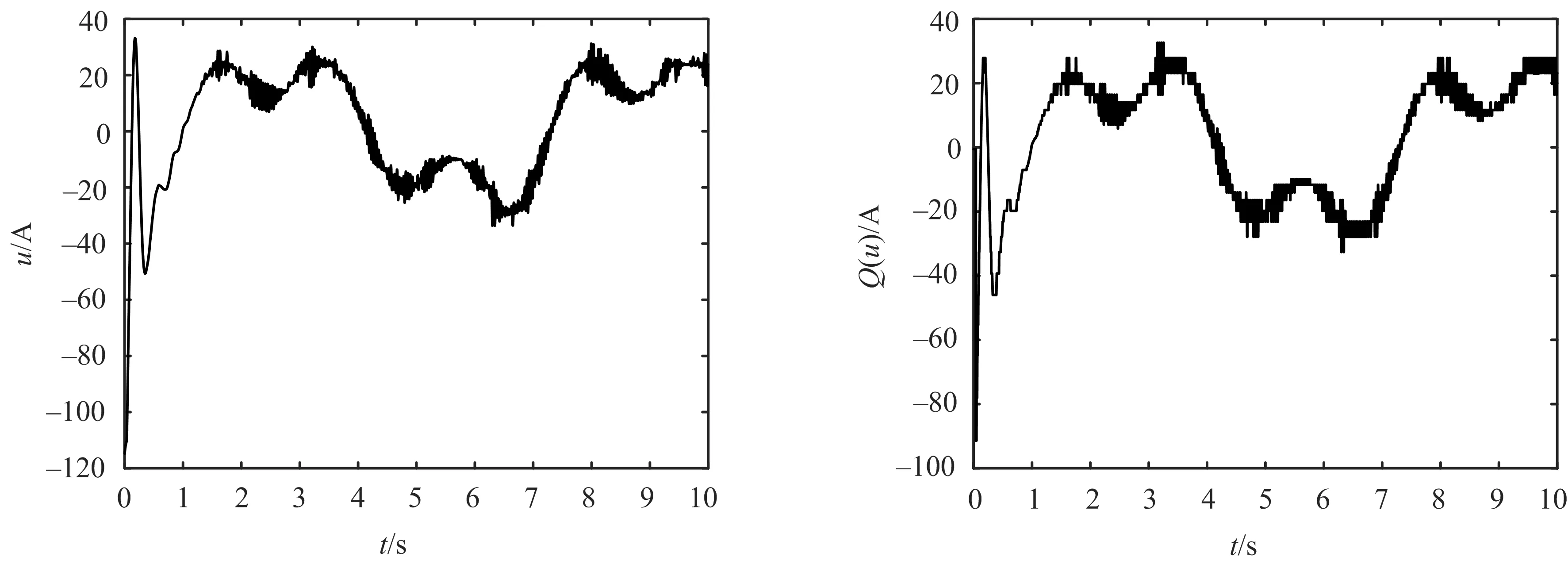
图4 控制输入 图5 量化输入

考虑外部干扰后的系统为

(52)

其中：w1,w2为外部干扰.

将该文提出的自抗扰预设定有限时间量化控制策略的抗干扰效果与神经网络策略的抗干扰效果进行仿真对比，仿真时二者参数、系统初始条件及期望信号均相同.2种控制策略的控制效果如图6～7所示.由图6～7可知，神经网络策略在外部扰动作用下系统发散，而该文策略能保证系统有界且控制效果良好，表明该文策略比神经网络策略有更好的控制性能.

图6 2种策略的输出状态跟踪效果 图7 2种策略的跟踪误差

为了证明该文策略具有有效性，将其应用于一个单杆机械臂系统，其数学模型[25]为

(53)

选取初始状态为:[x1(0),x2(0)]=[0.5,0.4];选取期望信号为yd=2sint.选取系统参数为：T2=T3=1;选取控制参数为：c1=10，c2=30;其余参数均同上.机械臂系统的仿真结果如图8～10所示.由图8～10可知，在量化输入较小的情况下，机械臂的输出误差很小，即系统输出有很好的跟踪效果.

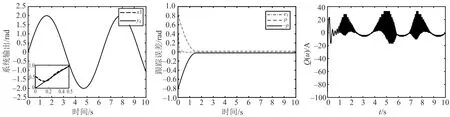
图8 机械臂输出状态跟踪效果 图9 机械臂跟踪误差 图10 机械臂量化输入

4 结束语

该文提出了一种自抗扰预设定有限时间量化控制策略，设计的控制器能使跟踪误差满足预设定有限时间控制要求的动态和稳态性能，系统有界稳定.在外部扰动作用下，神经网络策略系统发散，而该文策略能保证系统有界且控制效果良好，表明该文策略比神经网络策略有更好的控制性能.该文策略可应用于对暂态、稳态和抗干扰性能要求均较高的控制系统.