一类 ψ-Caputo分数阶微分方程解的存在性和Ulam-Hyers稳定性
李晓艳,任 玮,谢 地,蒋 威
(安徽大学 数学科学学院,安徽 合肥 230601)
分数阶微积分由于在方程理论和实际应用中都有极大的发展潜力,得到了众多研究学者的关注[1-2].分数阶微积分不仅在数值分析和应用数学中有着不可或缺的地位,而且在物理、化学、生物、工程和其他领域也发挥着显著的作用[3-6].
自从1695年分数阶微积分的概念被提出以来,分数阶积分和导数便衍生出了各种不同类型的定义.随着研究的不断深入,分数阶积分和导数涌现出了更多新的形式.这些分数阶积分和导数都有一个相同的内核,可以在此基础上使定义范围[1-2,7-10]更加广泛.因此,Almeida[11]利用与Caputo相关的分数阶导数的概念,提出了ψ-Caputo导数的定义(它是对关于函数ψ的一类分数阶导数的推广)及一种处理此类算子的数值方法,包括用依赖于一阶导数的和来近似分数导数,且通过实例验证了该方法的有效性和适用性.通过考虑人口增长模型,给出了该分数阶导数的一个应用,表明可以使用分数算子的不同核来更精确地建模.
论文的主要研究对象是探究一类特殊的Caputo分数阶微分方程的初值问题,利用相互转化的思想,将Caputo分数阶导数与Riemann-Liouville分数阶导数结合起来考虑.接下来便可以在研究此分数阶微分方程初值问题解的存在唯一性上寻找突破口,没有直接从ψ-Caputo导数的定义入手,以免带来更多烦琐的计算.最后,考虑到对分数阶微分方程解的存在性和稳定性的研究一直受到极高的关注[12-15],作者进一步探讨了Ulam-Hyers-Rassias,Ulam-Hyers,Semi-Ulam-Hyers-Rassias与分数阶微分方程稳定性涉及的相关问题[16-18].
首先,作者在一个实Banach空间X上考虑以下关于函数ψ的非线性Caputo分数阶微分方程
(1)

定义1[1]若α∈,Re(α)>0,-∞≤a
(2)
定义2[1]若α∈,n-1
(3)
若n-1<α (4) 作者将利用Krasnoselskii不动点定理来考虑关于函数ψ的非线性Caputo分数阶微分方程(1),则首先需要构造一个既定的空间 X={x|x(t)∈C[a,b]}, 其中 可以很容易证明(X,‖·‖X)是一个Banach空间. 引理1[2]若α>0,β>0,有 (5) 引理2[19]若0≤t1 (6) 引理3若f∈C[a,b],n-1<α (7) 证明由Riemann-Liouville分数积分和Caputo分数导数的定义,有 对等式右侧重复进行分部积分,可得 引理4若f∈C[a,b],n-1<β<α (8) 证明由Riemann-Liouville分数阶积分和Caputo分数阶导数的定义,有 (9) 将上面的等式代入到(9)中,由引理2可以推导出 注特别地,若f∈C[a,b],0<α<1,有 定义3[20]已知X是一个非空集,则d:X×X→[0,∞]是一个在X上的广义度量,若 (1)d(x,y)=0当且仅当x=y; (2)d(x,y)=d(y,x),对任意x,y∈X; (3)d(x,y)≤d(x,z)+d(z,y),对任意x,y,z∈X. 定理1[20](X,d)是一个广义上的完备度量空间,假设T:X→X是一个Lipschitz常数L<1的压缩算子.若存在一个非负整数k,使得对于x∈X,d(Tk+1x,Tkx)<∞,那么以下3个命题成立: (1)序列Tk收敛于T中的一个不动点x*; (2)x*是T在X*={y∈X|d(Tkx,y)<∞}上的唯一不动点; 定理2[21]已知K为Banach空间X上的非空有界闭凸子集,A,B:K→X满足: (1)对任意x,y∈K,都有Ax+By∈K; (2)算子A是压缩的,其中Lipschitz常数L<1; (3)B是K上的连续紧算子. 作者利用 Krasnoselskii不动点定理来证明关于函数ψ的非线性Caputo分数阶微分方程的初值问题解的存在唯一性,在有限区间[a,b]上分析了关于Ulam-Hyers-Rassias和Semi-Ulam-Hyers-Rassias稳定性的相关定理. 需要做出以下假设: (H1)L0和M为给定的正常数.假设f:J×X→X是分别满足以下条件的连续可微函数 ‖f(t,x1(t))-f(t,x2(t))‖≤L0‖x1(t)-x2(t)‖,∀t∈J, 以及 ‖f(t,x(t))‖≤M,∀t∈J. (H2)给定的正常数L,其中0 引理5假设函数x:J→X是连续可微的,则初值问题(1)等价于积分方程 (10) 根据初值条件x(a)=0,则进一步可得 基于上述论证可知,一个连续可微函数满足初值问题(1),当且仅当该函数满足积分方程(10). 定理3假设条件(H1)和(H2)均成立,则初值问题(1)存在唯一解. 证明根据引理1,可知初值问题(1)等价于积分方程(10).因此,可以将寻求初值问题(1)的解转化为探讨算子A和B的不动点问题,其中算子A和B的定义如下 (11) (12) 通过引用Krasnoselskii不动点定理,将证明方程(1)有唯一解.因此首先需要找到一个非空的有界闭凸子集K,其中 K={x(t)∈C[a,b]:‖x(t)‖≤R}, 且常数R满足 由算子A的定义可知,对于任意x∈K,都有Ax∈K,即算子A:K→K. 接下来证明算子A在K上是严格压缩的.对于任意x1,x2∈K,鉴于假设条件(H1)和(H2),从而可以推导得 因此,对于任意x1,x2∈K,有 ‖Ax1(t)-Ax2(t)‖ 这表明A是一个严格的压缩映射. 其次,显然可知算子B在Banach空间X中是连续的,还需要证明B(K)为列紧集.根据Arzela-Ascoli定理,只需推导出B(K)是一致有界且等度连续的即可. 一方面,对于∀x(t)∈K,有 所以,B(K)是一致有界的. 另一方面,对∀t1,t2∈J,若t1 因此,当t2→t1时,有‖Bx(t2)-Bx(t1)‖→0,从而B(K)是等度连续的,证明了B是K上的连续紧算子. 最后,对于∀x,y∈K,有 所以Ax+By∈K.综上所述,算子A+B在Banach空间X的有界闭凸子集中有一个不动点x,满足(A+B)x=x.因此,初值问题(1)存在唯一解. 例考虑关于Caputo微分方程的初值问题 这里取ψ(t)=lnt,α=0.8,β1=0.5,β2=0.2,其中t∈[1,2],f(t,x(t))=0.1sinx(t).通过验证给出的假设(H1)和(H2),即对于∀x1,x2∈X,有 ‖sinx1(t)-sinx2(t)‖≤‖x1(t)-x2(t)‖, 可以得出该初值问题在t∈[1,2]上存在唯一解. 该节介绍闭区间[a,b]上有关Ulam-Hyers-Rassias稳定性和半Ulam-Hyers-Rassias稳定性的基本概念,从而给出与系统(1)的稳定性相关的定理.为了研究稳定性的相关结论,需要在Banach空间X上建立适当的度量. Banach空间X上的度量d1(·)定义如下 d1(x,y)=inf{C∈[0,+∞)|‖x(t)-y(t)‖≤CΦ(t),t∈[a,b]}, (13) 其中:C是一个常数,Φ(t)是一个恒正的单调不减的连续函数. Banach空间X上的度量d2(·)定义如下 (14) 定义4[22]对于每个连续可微函数x:J→X,满足 (15) 其中:Φ(t)为恒正单调不减的连续函数. 若存在初值问题(1)的一个解x0以及一个常数C>0,使得 ‖x(t)-x0(t)‖≤CΦ(t),∀t∈J, 则称系统(1)具有Ulam-Hyers-Rassias稳定性.如果Φ(t)在上述不等式中为一个常值函数,则称系统(1)具有Ulam-Hyers稳定性. 定义5[22]对于每个连续可微函数x:J→X,满足 (16) 其中:常数θ≥0. 若存在初值问题(1)的一个解x0以及一个常数C>0,对于恒正单调不减的连续函数Φ(t),使得 ‖x(t)-x0(t)‖≤CΦ(t),∀t∈J, 则称初值问题(1)具有半Ulam-Hyers-Rassias稳定性. 定理4若假设(H1)和(H2)成立,Φ(t)是一个定义在[a,b]上恒正的单调不减的连续函数, 以及连续可微函数x:J→X,满足 则存在初值问题(1)的唯一解x0∈X,使得 (17) 且系统(1)具有Ulam-Hyers-Rassias稳定性. 证明考虑算子T:X→X,有 根据Banach空间X上的度量d1(·)以及假设(H1)与(H2)可知,对于∀x,y∈X,有 LCΦ(t),∀t∈J,L∈(0,1), 从而进一步可知 d1(Tx,Ty)≤LC=Ld1(x,y),L∈(0,1). 此外由条件(17)知 因此可以证实 由定理1可知,存在系统(1)的唯一不动点x0,使得Tx0=x0,且可以推导出 综上,作者完成了关于Caputo分数阶微分方程(1)的Ulam-Hyers-Rassias稳定性的证明. 定理5若假设(H1)和(H2)成立,Φ(t)是一个定义在[a,b]上恒正的单调不减的连续函数, 以及连续可微函数x:J→X,满足 其中:常数θ>0,则存在初值问题(1)的唯一解x0∈X以及常数M>0,使得 (18) 且系统(1)具有半Ulam-Hyers-Rassias稳定性. 证明考虑算子T:X→X,有 与定理4的证明类似,根据Banach空间上的度量d2(·)以及假设(H1)与(H2)可知,对于∀x,y∈X,有 进一步可以得出 LC,∀t∈J,L∈(0,1), 即 d2(Tx,Ty)≤LC=Ld2(x,y),L∈(0,1). 由于Φ(t)是一个恒正的单调不减的连续函数,可以找到一个常数M>0,满足 此外由条件(18)知 从而可以证实 由定理1可知,存在系统(1)的唯一不动点x0,使得Tx0=x0,且可以推导出 基于以上分析,作者论证出Caputo分数阶微分方程(1)具有半Ulam-Hyers-Rassias稳定性.1 预备知识

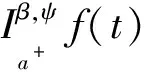
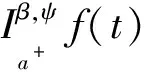
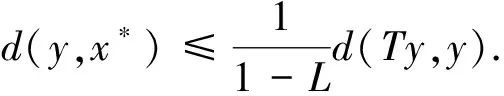
2 主要结果
2.1 Caputo分数阶微分方程解的存在性

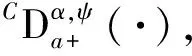
2.2 Caputo分数阶微分方程的Ulam-Hyers稳定性

