超大型环件径轴向轧制过程偏移机理及自适应模糊控制方法研究
张 科 汪小凯 华 林 韩星会 宁湘锦
1.武汉理工大学现代汽车零部件技术湖北省重点实验室,武汉,430070 2.武汉理工大学汽车零部件技术湖北省协同创新中心,武汉,430070 3.武汉理工大学材料绿色精密成形技术与装备湖北省工程中心,武汉,430070
0 引言
高质量、高性能超大型环件作为高端装备的关键基础零部件,在航空航天、风电、石油化工等领域的需求量不断增加[1],如运载火箭燃料贮箱过渡环、风电轴承与法兰以及石油化工压力容器等,其制造水平的提高对实现我国由制造大国向制造强国的转变具有重大意义。
径轴向轧环是一种先进的高性能环件近净成形技术,具有省力、优质、高效、绿色的特点,能获得几何精度高且组织性能优良的精密无缝环件,在机械、能源、船舶以及航空航天等领域得到广泛应用[2-4]。
近年来,国内外众多学者采用理论分析、仿真模拟和试验等方法对环件径轴向轧制成形理论和技术开展了广泛而深入的研究。HUA等[5]通过理论分析和仿真模拟的方法对环件轧制时的刚度模型及刚度条件进行了研究。邓加东等[6]采用仿真模拟的方法研究了环坯温度分布状态对径轴向轧制变形的遗传影响。郭良刚等[7]通过理论分析提出了一种基于轧比和径轴向变形量分配比的环件轧制毛坯尺寸设计方法,并采用仿真模拟进行了验证。汪小凯等[8]通过理论分析提出了一种热轧环过程中的环件尺寸公差控制计算方法,并结合试验进行了验证。钱东升等[9]采用仿真模拟和试验的方法对典型的大型双滚道风电轴承套圈的滚道轧制成形进行了研究。DAVEY等[10]采用ALE自适应网格技术来进行环件轧制建模,解决了环件轧制过程中因大变形导致网格畸变而无法计算的问题。BERTI等[11]提出了一种分析方法来预测环件轧制过程中关键运动参数的变化。LIANG等[12]针对超大型铝合金环件轧制力的控制要求和以往试错模拟效率低的问题,在有限元软件下开发了智能实时力控有限元模型。
以上研究促进了环件径轴向轧制成形理论和技术的发展。实际超大型环件径轴向轧制过程中极易出现环件偏移现象,直接影响到轧制稳定性和几何精度,严重时甚至会导致环件报废。关于超大型环件轧制过程的环件偏移机理及其控制方法鲜有文献报道,为此,本文通过研究超大型环件径轴向轧制过程中锥辊转速对环件偏移的影响规律,建立了理想情况下不发生环件偏移的锥辊旋转运动学条件,通过在有限元软件中开发自适应模糊控制器来实时调节锥辊转速,环心偏移量被有效控制在较小范围,从而极大提高了超大型环件径轴向轧制过程的稳定性和成形质量。
1 锥辊转速对环件轧制过程偏移的影响
1.1 环件偏移现象描述
环件径轴向轧制原理如图1所示。驱动辊做主动旋转运动,芯辊做被动旋转运动和径向水平进给运动,上下锥辊做主动旋转运动和径向水平后退运动,同时上锥辊做向下的轴向进给运动,左右导向辊与环件外壁接触,跟随环件直径长大做后退运动,保证环件圆度。环件通过径向和轴向孔型的连续局部加载,达到壁厚与高度减小、直径扩大及截面轮廓成形的效果。

图1 环件径轴向轧制原理图Fig.1 Schematic diagram of radial-axial ring rolling
通常情况下,驱动辊转速是恒定不变的,而锥辊转速需要与驱动辊转速相匹配,否则环件很容易出现偏移,如图2所示。假设环心O坐标为(x0,y0),当环件没有出现偏移时,y0为0;当环件为上偏状态时,y0为正;当环件为下偏状态时,y0为负。同时,用dy0表示偏移量变化率,用|y0|表示环心偏移量大小。

图2 环件偏移示意图Fig.2 Schematic diagram of ring’s offset
1.2 环件轧制过程理论锥辊转速设计
合理设计超大型环件轧制过程中的锥辊转速是保证轧制稳定性的重要条件。如图3所示,假设驱动辊转速为nd,驱动辊半径为Rd,锥辊转速为nc,锥辊半锥角为θ,锥辊顶点到环件外径之间距离为L,环件外半径、内半径、壁厚以及高度分别为R、r、b、h。忽略环件与驱动辊之间的相对滑动,假设环件沿壁厚方向的切线速度呈线性分布,并假设环件端面与锥辊外表面线速度相等的点为A点,则锥辊转速nc可表示为

图3 环件与轧辊的接触位置示意图Fig.3 Schematic diagram of contact position between ring and rolls
(1)
式中,s为A点与环件外径之间的距离。
为研究等速位置A点对环件轧制过程偏移的影响,引入速度匹配系数ks[13],其定义为
(2)
进而锥辊转速可表示为
(3)
1.3 前滑区与后滑区对环件轧制运动的影响及其分布变化规律
环件径轴向轧制过程中,锥辊与环件之间接触变形区域的几何形状为锥辊外锥面的一部分[14],如图4所示。通常,在接触变形区域内同时存在前滑区和后滑区。在前滑区内,环件线速度超前于锥辊线速度,环件受到阻碍其旋转的滑动摩擦力F1;在后滑区内,环件线速度落后于锥辊线速度,环件受到推动其旋转的滑动摩擦力F2。

(a)俯视图 (b)侧视图图4 轴向孔型接触区域示意图Fig.4 Schematic diagram of the axial roll’s contact region
图5给出了某一环件在某一时刻不同速度匹配系数下环件端面与锥辊外表面的线速度分布曲线。可以看出,当速度匹配系数从0增大到1的过程中,锥辊转速不断增大,滑移区分布呈现出一定的变化:当速度匹配系数为0时,滑移区全部为前滑区,环件受到的阻碍作用最大;当速度匹配系数为1时,滑移区全部为后滑区,环件受到的推动作用最大;当速度匹配系数位于0到1之间时,滑移区内同时存在前滑区和后滑区,环件受到的主导作用是阻碍还是推动,取决于前滑区和后滑区的相对大小。

图5 环件端面与锥辊外表面的线速度分布曲线Fig.5 Linear velocity distribution curves between ring end face and axial roll’s surface
为研究不同位置点的速度差,在后滑区内取B点,在前滑区内取C点,B点和C点与A点之间距离均为d,如图3所示。假设A点的线速度为v,则B点处环件端面线速度vB1为
(4)
B点处锥辊外表面线速度vB2为
(5)
vB1与vB2之间的速度差ΔvB为
(6)
引入滑移点位置系数kd,定义为
(7)
因此,后滑区内B点的速度差ΔvB可表示为
(8)
ks∈[0,1]kd∈[0,ks]
前滑区内C点的速度差ΔvC可表示为
(9)
ks∈[0,1]kd∈[0,1-ks]
在等速点位置确定后,即速度匹配系数ks确定后,通过速度差的表达式可以看出减小速度差的方法大致有两种[15]:当R=L时,速度差为0,这要求锥辊顶点始终落在过环心的轴线上,且后退速度与环件长大速度一致,这种情况只适用于中小型环件轧制,不适合超大型环件轧制;当环件壁厚b较小时,速度差可以维持在较小范围内,但在超大型环件轧制中,坯料壁厚通常较大,受到锥辊与环件接触区域速度差的影响较大。因此,只有通过选择合理的速度匹配系数来确保前滑区与后滑区对环件产生的作用相当,从而抑制环件偏移,提高轧制稳定性。
1.4 理想情况下不产生环件偏移时锥辊旋转运动学条件
为了简化计算模型,将接触变形区域进行投影,近似得到一个直角梯形,并用来代替轴向孔型处的接触变形区域,为便于分析,假设前滑区与后滑区分界线为直线,如图6所示。设前滑区面积为S1,后滑区的面积为S2,则有

图6 轴向孔型接触区域简化图Fig.6 Simplified diagram of the axial roll’s contact region

(10)
(11)
式中,Δh为上锥辊压下量;rc为锥辊在环件外径处等效半径,rc=Lsinθ。
为了研究理想情况下不产生环件偏移时锥辊旋转的运动学条件,对轧制成形过程中的环件进行受力分析,如图7所示。在受力模型中,将径向孔型处等效为一个支点,设左右导向辊对环件的力为Fg,前滑区滑动摩擦力为F1,后滑区滑动摩擦力为F2。

图7 环件受力模型示意图Fig.7 Schematic diagram of ring force model
超大型环件轧制过程中,假设环件受到的导向力Fg相等且指向环心,那么环件是否会发生绕径向孔型处支点O偏移主要取决于环件在轴向孔型滑移区内摩擦力对支点O的力矩是否平衡。设前滑区摩擦力F1对支点O的力矩为M1,后滑区摩擦力F2对支点O的力矩为M2,则有
(12)
(13)
式中,p为环件在滑移区受到的压力。
令D=2R,d=2r,由M1=M2,化简可得
(14)
式(14)是一个关于速度匹配系数ks的方程,以φ10 m超大型环件径轴向轧制为例,代入环件轧制过程中不同阶段的外直径D、内直径d和壁厚b的值,可得不同轧制阶段的最优速度匹配系数(表1)。可以看出,随着环件的长大和壁厚的减小,最优速度匹配系数不断增大,并逐渐接近0.5。

表1 不同轧制阶段的最优速度匹配系数Tab.1 Optimal velocity matching coefficients at different rolling stages
2 基于锥辊转速自适应模糊调节的环心偏移量控制方法
锥辊转速大小直接影响环件轧制过程的运动平衡,合理调节锥辊转速可有效改变轴向孔型滑移区中前滑区和后滑区的受力,以此调节轧环过程产生的环件偏移。将自适应模糊控制运用于超大型环件径轴向轧制过程中的环心偏移量控制具有重要意义,本文基于锥辊转速自适应模糊调节的环心偏移量控制方法如图8所示。

图8 自适应模糊控制框图Fig.8 Adaptive fuzzy control block diagram
2.1 自适应模糊控制器的设计
超大型环件轧制过程中发生偏移后,轧制稳定性无法得到保证,严重时甚至会导致轧制过程终止,产生报废环件。因此,当环件出现偏移后,需要对锥辊转速进行干预,使环心偏移量维持在允许的范围内。
环件轧制过程历史数据中蕴含了大量有效的人工控制经验,可通过分析采集系统中的数据来提取控制规则。为此,在某公司的10 m辗环机上开展了φ5 m的轧环试验,如图9所示。试验数据中环心偏移量y0与锥辊转速nc随外直径D的变化曲线如图10所示。从该曲线的整体变化趋势可以看出,随着环件的不断长大,锥辊转速逐渐减小;从该曲线的个别之处可以看出,当环件出现上偏即环心偏移量为正值且不断增大时,锥辊转速需要大幅减小。

图9 φ5 m环件径轴向轧制试验Fig.9 Radial-axial ring rolling test of φ5 m ring

(a)数据样本一
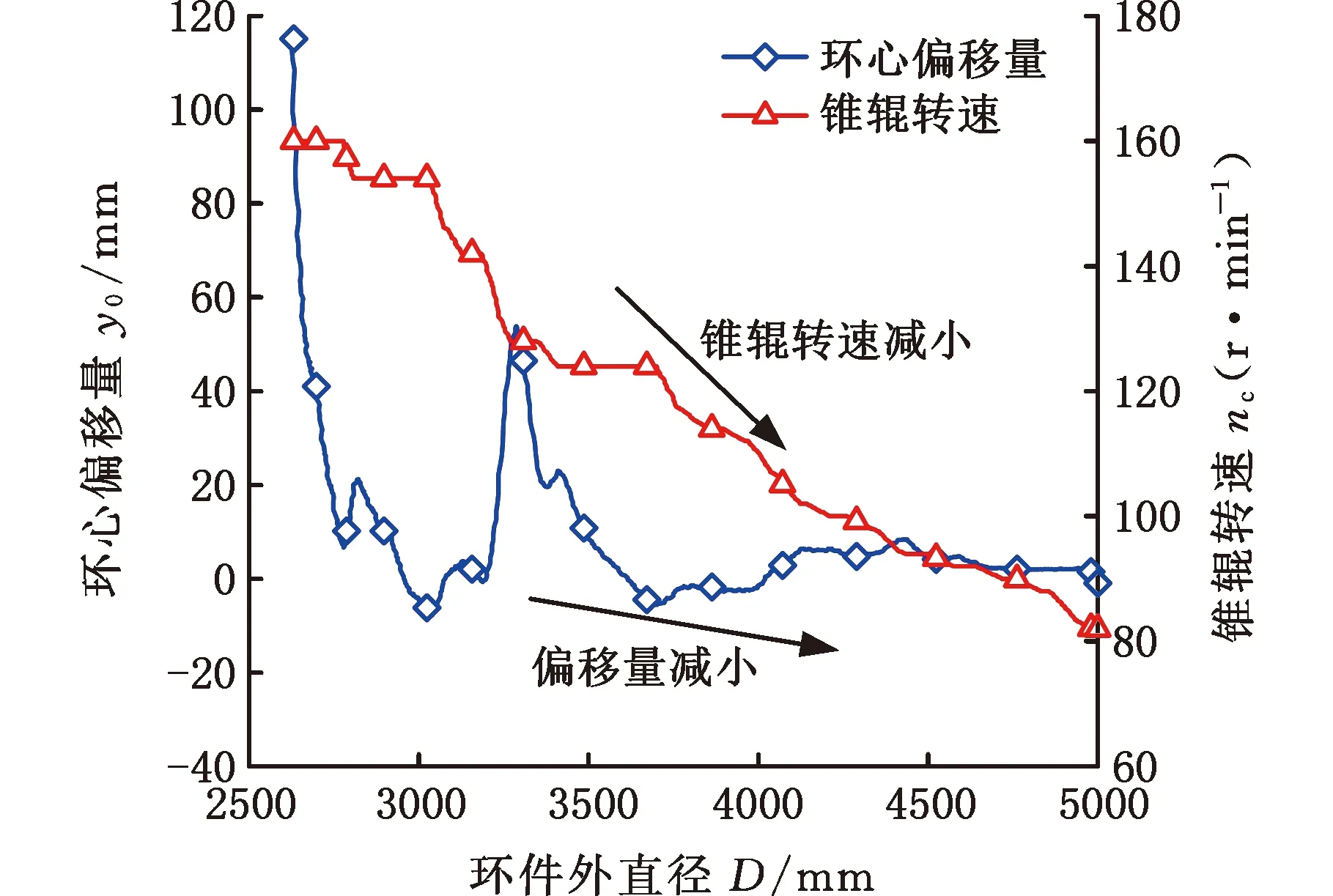
(b)数据样本二图10 两组φ5 m环件径轴向轧制试验数据样本Fig.10 Two groups of data samples of radial-axial ring rolling test for φ5 m ring
分析试验样本数据并结合环件轧制过程偏移机理,可总结出表2所示的环件轧制过程环心偏移量控制经验。

表2 环件轧制过程环心偏移量控制经验Tab.2 Control experiences of ring center offset in the ring rolling process
为设计一个双输入单输出的模糊控制器,选定环心偏移量y0与环心偏移量变化率dy0作为输入量,锥辊转速调节量w作为输出量。定义控制器输入、输出的模糊子集:
y0={NL,NM,NS,ZO,PS,PM,PL}
dy0={NL,NS,ZO,PS,PL}
w={NL,NM,NS,ZO,PS,PM,PL}
其中,NL表示负大;NM表示负中;NS表示负小;ZO表示零;PS表示正小;PM表示正中;PL表示正大。建立模糊控制规则如表3所示。

表3 模糊控制规则Tab.3 Fuzzy control rules
采用三角形隶属函数对输入量与输出量模糊子集进行划分,设环心偏移量y0模糊论域为[-3,3],环心偏移量变化率dy0模糊论域为[-2,2],锥辊转速调节量w模糊论域为[-3,3]。模糊控制器根据实时的输入量进行实时计算后发挥在线调速控制作用,其具体工作过程如下。
(1)模糊化。环心偏移量y0和环心偏移量变化率dy0分别经过量化因子k1、k2映射到各自的模糊论域,见图11。

图11 模糊化过程Fig.11 Process of fuzzification
(2)模糊推理。采用Mamdani推理法根据输入量进行近似推理得到输出模糊集合,见图12。

图12 模糊推理过程Fig.12 Process of fuzzy inference
(3)清晰化。采用最大隶属度平均值法进行清晰化,最后经过比例因子k3转化得到实际锥辊转速调节量w,如图13和下式所示:

图13 清晰化过程Fig.13 Process of defuzzification
w=k3(p+q)/2
(15)
式中,p、q为最大隶属度图形顶点与隶属度函数曲线交点的横坐标。
超大型环件轧制过程中,环心偏移量会逐渐增大,对于锥辊转速调节量比例因子k3,如果一直使用同一个值,势必会出现在轧制前期对环心偏移量的控制效果较好,但在轧制后期的控制力度会达到极限而不能很好地控制环心偏移量幅值的情况。为了使环心偏移量在整个轧制成形模拟期间都能被控制在较小范围内,提出使用一种能自适应变化的比例因子k3,其表达式为
(16)
式中,k3b为比例因子k3的基本值;Y0为某一偏移量控制阈值;a为自适应参数。
2.2 自适应模糊控制有限元模型的建立
建立φ10 m超大型环件径轴向轧制三维热力耦合有限元模型,见图14。环件材料为42CrMo,其与温度相关的材料属性(如比热容、热导率、弹性模量和泊松比)及高温流动应力应变模型参考文献[16];环件被视为变形体,其网格类型选用八节点六面体热力耦合线性减缩积分单位C3D8RT;轧辊被视为等温解析刚体,同时每个轧辊被分别赋予参考点(RP)来控制其运动。环件径轴向轧制有限元模拟的主要参数见表4。
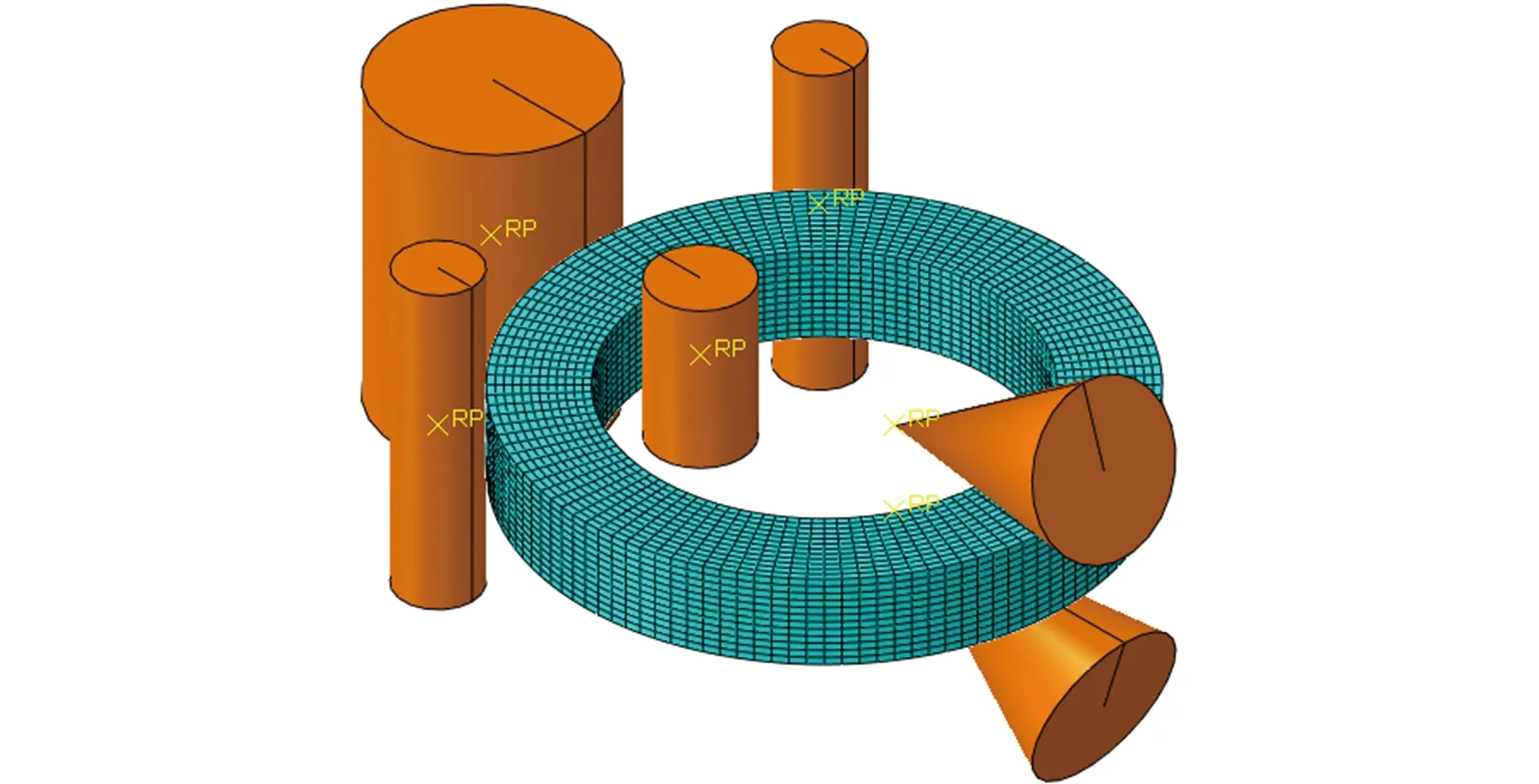
图14 环件径轴向轧制有限元模型Fig.14 Finite element model of radial-axial ring rolling

表4 环件轧制主要参数Tab.4 Main parameters of ring rolling
建立φ10 m超大型环件径轴向轧制过程自适应模糊控制有限元仿真模型包括以下关键步骤:
(1)通过在ABAQUS软件中设置虚拟传感器来测量环件外表面各点坐标、轧辊位移,从而获得环件实时半径、壁厚、圆度、环心偏移量以及环心偏移量变化率。
(2)基于ABAQUS软件和VUAMP子程序开发,将设计的双输入单输出模糊控制器以程序形式植入原有控制程序中,实现对锥辊转速的实时调控。
另一个解法是质点滤波(PF),即序贯蒙特卡罗方法,用一组加权质点近似后验分布(Doucet et al,2001)。当质点的数目趋于无穷时,由质点滤波得到的解也趋于最优解。关于质点滤波及其变种的文献很多(Liu and Chen,1998;Doucet et al,2001;Arulampalamet al,2002)。这个方法的基本过程简述如下做参考。
(3)在实际环件轧制过程中,锥辊转速调节频率如果过高则会引起冲击波动,反而会影响环件轧制稳定性和圆度,所以需要对锥辊转速调节量进行递推平均滤波以减小锥辊对环件造成的冲击和振荡[17]。递推平均滤波的公式为
(17)
式中,i为每个采样周期编号;j为每个采样周期采样次数;wk为每个采样周期内按序号k排列的锥辊转速调节量输出值。
经过前期大量的有限元仿真模拟,确定比例因子k3的基本值为0.1,某一偏移量控制阈值Y0为20,自适应参数a为0.005。
3 仿真结果与分析
3.1 不同速度匹配系数对超大型环件轧制成形的影响
图15所示为环心偏移量在不同速度匹配系数下随环件外直径的变化曲线。可以看出,速度匹配系数的不同导致环心偏移量幅值与变化趋势有所差异。在环件外径长大到7 m之前,随着速度匹配系数的增大,环件偏移状态由上偏转变为下偏,当速度匹配系数为0.5时,环心偏移量较小。这是因为随着速度匹配系数的增大,前滑区面积逐渐减小而后滑区面积逐渐加大,环件受到阻碍其旋转的滑动摩擦力逐渐减小,受到推动其旋转的滑动摩擦力逐渐增大。在环件的外径长大到7 m之后,由于环件的转动惯量达到一定程度,环件开始出现周期性的晃动。

图15 不同速度匹配系数下的环心偏移量Fig.15 Ring center offset at different velocity matching coefficients
图16所示为圆度误差在不同速度匹配系数下随环件外直径的变化曲线。可以看出,在不同速度匹配系数下的圆度误差都表现为先急剧增大,之后维持在一定范围内波动。

图16 不同速度匹配系数下的圆度误差Fig.16 Circularity error at different velocity matching coefficients
综合表1中不同轧制阶段最优速度匹配系数的变化趋势和区间范围以及图15的分析结果,进一步绘制了速度匹配系数为0.4、0.45、0.5时环心偏移量随环件外直径的变化曲线,如图17所示。可以看出,速度匹配系数为0.45时环心偏移量相对较小,故选定0.45作为后续自适应模糊控制有限元仿真模拟的速度匹配系数。

图17 速度匹配系数0.4、0.45、0.5下的环心偏移量Fig.17 Ring center offset at velocity matching coefficients of 0.4,0.45 and 0.5
3.2 基于锥辊转速自适应模糊调节的环心偏移量控制方法对超大型环件轧制成形的影响
图18为环心偏移量在常规控制和自适应模糊控制下随环件外直径的变化曲线对比图。可以看出,在常规控制下,随着环件逐渐长大,环心偏移量在前期可以维持在较小范围内,但环心偏移量在后期不断增大,整体向驱动辊入口处偏移;在自适应模糊控制下,环件虽然也有向驱动辊入口处偏移的趋势,但偏移幅度在每个阶段都被控制在相对很小的范围内,保证了轧制过程的稳定性。另外可以发现,在自适应模糊控制下,当环件的外径达到9 m后,环件开始出现小程度的晃动,这是环件的转动惯量增大与刚度减小造成的[18]。

图18 不同状态下的环心偏移量Fig.18 Ring center offset in different states
图19为圆度误差在常规控制和自适应模糊控制下随环件外直径的变化曲线对比图。可以看出,圆度误差在常规控制和自适应模糊控制下变化趋势及范围的差异不大,说明在一定范围内环心偏移量对圆度误差影响较小。

图19 不同状态下的圆度误差Fig.19 Circularity error in different states
图20为锥辊转速在常规控制和自适应模糊控制下随环件外直径的变化曲线对比图。可以看出,在常规控制下,随着环件逐渐长大,锥辊转速几乎全程保持在一个定值附近,无明显变化;在自适应模糊控制下,随着环件逐渐长大,锥辊转速呈现出先小幅增大后逐渐减小的变化趋势,其变化趋势与环心偏移量变化趋势相同,验证了“环件上偏,锥辊加速;环件下偏,锥辊减速”的控制规则。同时,该变化趋势与试验数据也基本一致,验证了仿真和试验结果的一致性。另外可以发现,在自适应模糊控制下,当环件外径达到9 m后,锥辊转速出现了小范围内的波动,这是由于环件出现了晃动,锥辊为维持环心偏移量在一定范围内而被迫改变转速,导致变化频率较高。

图20 不同状态下的锥辊转速Fig.20 Axial roll speed in different states
从图21中可以看出,对φ10 m超大型环件径轴向轧制过程进行自适应模糊控制后,虽然全程平均圆度误差几乎没有变化,但全程平均环心偏移量明显减小,与常规控制相比,减幅达72.4%,控制效果显著。

图21 平均环心偏移量与平均圆度误差对比Fig.21 Comparison of average ring center offset and average circularity error
4 结论
(1)通过分析前滑区和后滑区的分布变化规律及对环件轧制运动的影响可知,增大速度匹配系数会导致前滑区减小、后滑区增大,环件受到锥辊的阻碍作用减弱、推动作用增强,以此揭示了超大型环件径轴向轧制过程的偏移机理。
(2)基于转矩平衡推导了理想情况下不产生环件偏移时锥辊旋转运动学条件,结果表明,在环件径轴向轧制过程中存在一个实时的最优速度匹配系数可使得环心偏移量相对较小。
(3)提出了超大型环件径轴向轧制过程环心偏移量自适应模糊控制器的设计方法,并采用ABAQUS软件和VUAMP子程序开发,建立了自适应模糊控制有限元模型。
(4)以φ10m超大型环件径轴向轧制为例,开展了基于锥辊转速自适应模糊调节的环心偏移量控制方法有限元仿真,对比了常规控制与自适应模糊控制下环心偏移量变化规律,结果表明,在自适应模糊控制下全程平均环心偏移量较常规控制减小了72.4%,仿真结果和试验数据均验证了所提超大型环件径轴向轧制过程偏移自适应模糊控制方法的有效性。

