非线性商用车仿生悬架等偏频等高度设计
宋 勇 陆 浩 李占龙 燕碧娟 孟 杰 连晋毅
太原科技大学机械工程学院,太原, 030024
0 引言
悬架是现代车辆的一个重要总成,在行驶过程中起衰减或隔离路面的振动冲击,控制车轮运动轨迹,确保车辆具有良好的平顺性和操纵稳定性的作用[1-4]。目前,国内外研究大多聚焦于乘用车悬架性能和品质的提高[5-6],然而,随着物流运输的快速发展,特别是危化品、精密仪器设备、易碎易损物品运输等的发展,商用车悬架性能和品质的提高显得尤为重要。
商用车悬架设计要求主要有:①车身从空载到满载时的振动频率变化小,以保证其平顺性。②簧载质量变化时,车身高度变化小,以保证其稳定性[7]。目前,商用车悬架设计多采用基于钢板弹簧的满载设计方法,因钢板弹簧多为线性弹性元件,致使悬架变簧载时车身偏频和高度变化大,车辆平顺性差,难以满足上述设计要求[8-9]。采用主动悬架,如空气悬架等,可通过其车身高度调节装置保证车身振动频率和高度不随簧载质量变化而变化,但因空气悬架成本高,故很少应用于商用车[10-12]。因此,研究一种变簧载条件下具有等偏频等高度特性的低成本、高品质悬架已成为商用车研发的重要课题。
本文团队前期研究发现,双菱形仿袋鼠腿悬架(简称“仿生悬架”)具有特殊的非线性行为特性,不同行驶工况下表现出良好的路面适应性、高速稳定性和舒适性,这为车辆悬架性能和品质的改善提供了思路和方法[13-14]。本文基于仿生悬架的静力学特性分析,提出一种商用车等偏频等高度设计方案并对该方案进行研究、分析与评价,以改善商用车的平顺性。
1 仿生悬架静力学分析与等偏频等高度设计理论
文献[15-16]对袋鼠腿部结构及功能进行了剖析与提炼,将袋鼠腿骨骼结构等效为1∶2∶1的三连杆结构(大腿骨连杆-小腿骨连杆-足骨连杆),并对称布置成菱形结构,如图1所示;将袋鼠腿关节(髋、膝、踝)简化为铰接结构;将袋鼠大腿、小腿、足部肌腱的弹性储能功能等效为大腿、小腿、足部肌腱弹簧;将袋鼠大腿、小腿肌肉的耗能作用通过大腿骨连杆与小腿骨连杆、小腿骨连杆与足骨连杆间的阻尼器来模仿;将袋鼠腿部肌肉力等效为肌肉力发生器,构建出双菱形仿袋鼠腿悬架的工程缓冲结构[17]。

1.足骨连杆 2.肌肉力发生器 3.小腿骨连杆 4.大腿骨连杆 5.车身 6.横置弹簧及阻尼器 7.纵置弹簧及阻尼器 8.车轮图1 仿生悬架结构演变Fig.1 Evolution of the bionic suspension structure
1.1 仿生悬架的几何关系
图2为仿生悬架的结构简图。以悬架下铰接点A为中心的各铰接点处相对位移及初始角度变化量如图3所示。图2中,l为仿生足骨杆AC、AB和仿生大腿骨杆EF、DF的长度,2l为仿生小腿骨杆CD和BE的长度,仿生结构的各铰接点位移分别为yi(i=t、1、2、3、F),k1、k2分别为纵置和横置弹簧的刚度,c1、c2分别为纵置和横置阻尼器的阻尼系数。图3中,θ0为未受载时仿生足骨杆AB与水平面的初始夹角,θ为双菱形受力后仿生足骨杆的转动角度,x1为仿生悬架铰接点B的水平位移。

图2 仿生悬架结构简图Fig.2 Schematic diagram of the bionic suspension

图3 仿生悬架被拉伸时下菱形的变形形态Fig.3 Deformation of the lower rhombus when the bionic suspension is stretched
由图3中各杆的位置关系可得
(1)
x1=l(cosθ0-cos(θ0+θ))
(2)
l2=(lsinθ0+y1-yt)2+(lcosθ0-x1)2
(3)
由式(3)得
(4)
1.2 悬架的仿生骨杆及各点受力分析
悬架系统的各仿生骨杆质量相对于车身质量很小,因此静力分析过程中忽略仿生骨杆及弹簧元件质量。为得到结构不平衡时的静输出力f,对图4中铰接点E、N、B、F进行受力分析,假设各个力的方向如图4所示。其中,f为仿生悬架上端作用力,-f为簧载质量对悬架的压力,-r为悬架及簧载质量对地面的压力,r为地面对悬架的支持力,f1、f8为仿生足骨杆AC的内力,f2、f5为仿生大腿骨杆DF的内力,f3为仿生大腿骨杆EF的内力,f4为仿生足骨杆AB的内力,f6、f7为仿生小腿骨杆BE的内力,Fx1、Fy1为销钉N对杆CD的作用力,Fx2、Fy2为销钉N对杆BE的作用力,k1y为纵置弹簧k1的输出作用力,y=2(y1-yt),2k2x2为横置弹簧的输出作用力,x2=2x1。

图4 各铰接点受力分析Fig.4 Force analysis of each node
根据长杆CD、BE在水平、竖直方向受力平衡,及对点N、D力矩平衡,得
f2sin(θ0+θ)+Fy1=k1y+f1sin(θ0+θ)
(5)
f3sin(θ0+θ)+Fy2=k1y+f1sin(θ0+θ)
(6)
f2cos(θ0+θ)+Fx1=f1cos(θ0+θ)+2k2x2
(7)
f3cos(θ0+θ)+Fx2=f1cos(θ0+θ)+2k2x2
(8)
f1lsin(2θ0+2θ)+f2lsin(2θ0+2θ)=
2k2x2lsin(θ0+θ)
(9)
Fy1cos(θ0+θ)+Fx1lsin(θ0+θ)=
2f1lsin(2θ0+2θ)
(10)
根据图4中F点受力得到结构的输出静力f的表达式:
(11)
(12)
由式(11)可以看出,仿生悬架结构的静力输出与初始角度、弹簧刚度和悬架变形密切相关,为便于分析函数与变量之间的关系,对公式进行量纲一化,得
(13)
式中,γ为初始正弦值,γ=sinθ0;Y为等效位移,Y=yF/l;α为纵置弹簧与横置弹簧刚度比,α=k1/k2;Fe为等效静力,Fe=f/(k2l)。
将等效静力Fe对等效位移Y求导得静刚度表达式:
(14)
将式(13)分为非线性部分An和线性部分Bn,有
(15)
(16)
1.3 仿生悬架的静态特性分析
由式(13)和式(14)可知,等效静力Fe和等效静刚度dFe/dY与悬架的初始角度正弦值γ、刚度比α及等效位移Y密切相关。由式(13)~式(16)可知γ和Y非线性地影响着Fe和dFe/dY,α则线性地影响着Fe。下面讨论γ、α和Y变化时悬架的静态特性。
1.3.1γ和α一定时悬架的静态特性
令初始角度为30°,刚度比α=1,等效位移Y压缩区间为0~2,拉伸区间为-2~0,则悬架结构非线性部分An、线性部分Bn和整体Cn=An+Bn的等效静力Fe与等效静刚度dFe/dY的变化如图5所示。

(a)非线性部分、线性部分和整体Fe与Y的关系

(b)非线性部分、线性部分和整体dFe/dY与Y的关系图5 γ和α一定时悬架静态特性曲线Fig.5 Suspension static characteristic curve when γ and α are fixed
由图5可知,该悬架的压缩行程大致为线性变化,拉伸行程为明显的非线性变化。由图5b可知,当满载位置选定在线性区间时,悬架刚度小且变化平缓,车辆平顺性良好;距离满载位置较远的拉伸行程极限,刚度特性曲线很快变陡,刚度急剧增大,该特性可使悬架在有限行程范围内得到比线性悬架更多的动容量,提高缓冲块抗击穿能力。
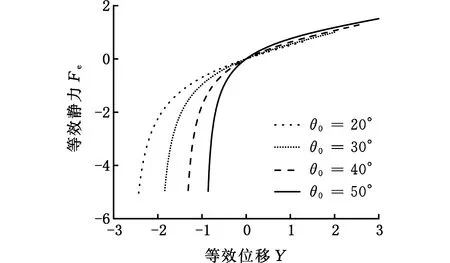
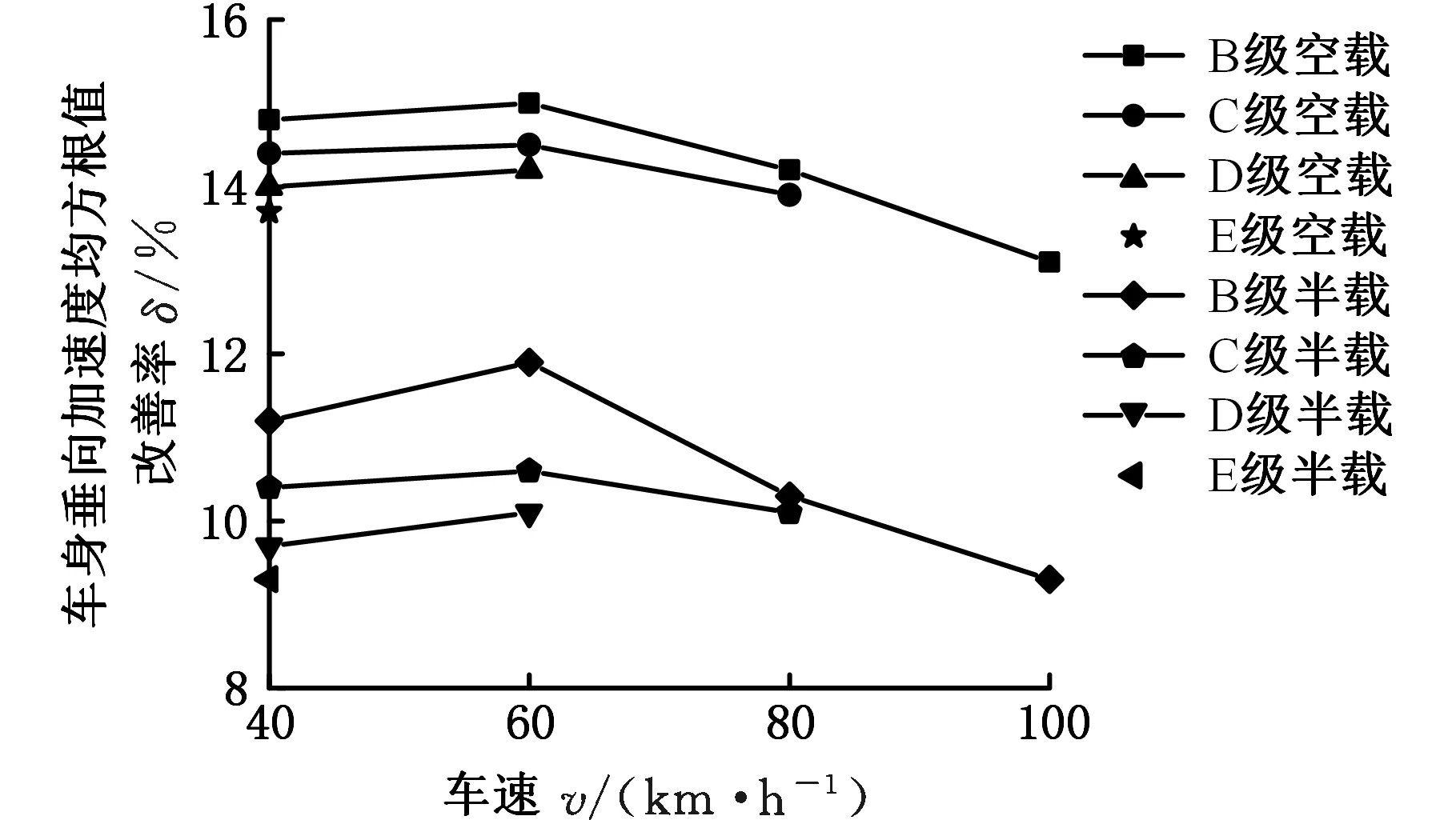
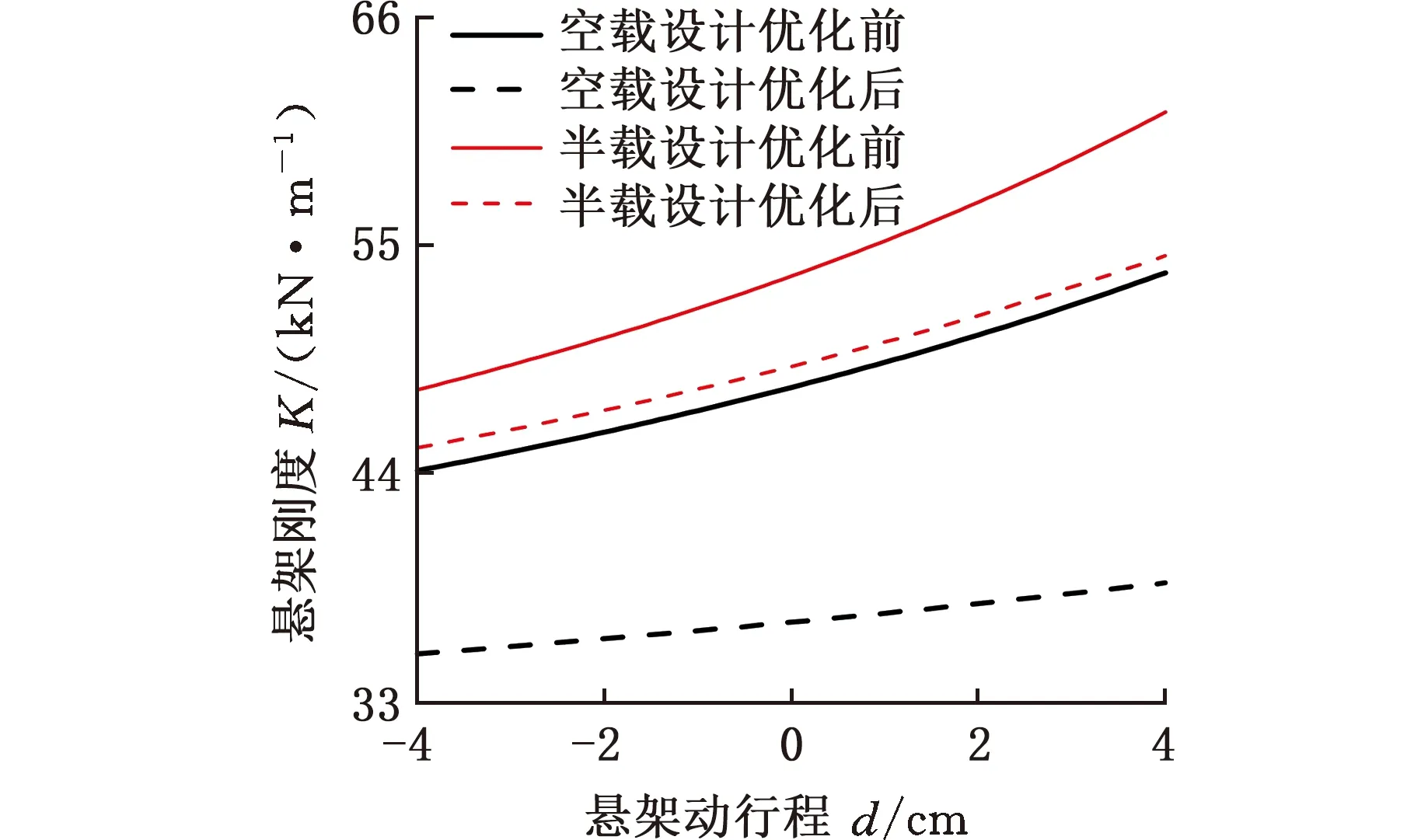
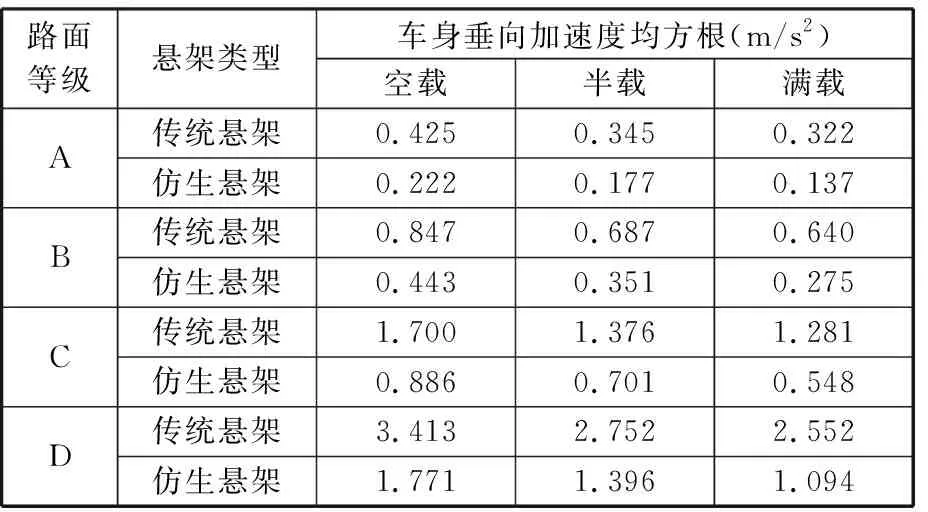
此外,由图5可知,0 1.3.2γ一定时悬架的静态特性 为探讨刚度比α对仿生悬架静态输出特性的影响,在式(13)和式(14)中,令初始角度为30°,等效位移Y压缩区间为0~2,拉伸区间为-2~0,刚度比α分别取0.5、1、2和4,得出悬架的等效静力Fe、等效静刚度dFe/dY随等效位移Y变化的曲线,如图6所示。 (a)不同α下Fe与Y的关系 (b)不同α下dFe/dY与Y的关系图6 γ一定时悬架的静态特性曲线Fig.6 Suspension static characteristic curve when γ is fixed 由图6a可知,随着α的增大,Fe的线性区间增大、非线性区间减小;相比于大刚度比,小刚度比下的非线性区间的非线性更强。由图6b可知,α的增大使dFe/dY的线性段刚度增大,但悬架的行程区间不变。 因此,α影响悬架的特性分布,具体应用时,可通过调整α来实现不同的悬架特性需求。 1.3.3α一定时悬架的静态特性 为探讨初始角度θ0对仿生悬架静态输出特性的影响,在式(13)和式(14)中,令刚度比α=1,θ0分别取20°、30°、40°和50°,等效位移Y压缩区间分别为0~1.37、0~2、0~2.57、0~3.06,拉伸区间分别为-2.63~0、-2~0、-1.43~0、-0.94~0,得到Fe、dFe/dY随Y变化的情况如图7所示。 (a)不同θ0下Fe与Y的关系 (b)不同θ0下dFe/dY与Y的关系图7 α一定时悬架静态特性曲线Fig.7 Suspension static characteristic curve when α is fixed 由图7可知,不同的θ0对应不同的Fe和dFe/dY曲线,随着θ0的增大,它们的线性区间增大、非线性区间减小;相比大的θ0,小θ0的非线性区间的非线性更强。此外,悬架的总行程不变,Y的变化区间随θ0的增大发生了右移,右移的大小随θ0的增大而增大,右移的相对大小随初始角度的增大而减小。 因此,θ0影响悬架的行程区间及其特性分布。具体应用时,可通过调整θ0来适应不同的工况。 以上分析表明:仿生悬架在不同θ0时均具有较理想的非线性弹性特性和刚度特性,在工程应用时,可根据不同的簧载质量选择恰当的θ0,以实现悬架的刚度可调。 偏频是表现汽车操控稳定性和平顺性的重要数据。一般来说偏频高,悬架刚度大,操控性能较好;偏频低,悬架刚度小,行驶平顺性更好[18]。偏频与悬架刚度的关系如下: (17) 式中,n为偏频;K为悬架刚度;m为簧载质量。 若悬架可等偏频变化,则要求悬架的刚度K可随簧载质量m的变化而变化。 由式(12)和式(17)可得仿生悬架偏频n计算式: n= (18) yF=4lsinθ0-h (19) 式中,h为车辆满载静平衡时悬架的高度。 由式(19)可知,当h不变时,即悬架为等高度设计,此时yF为θ0的函数,同时结合式(18)可知,n为θ0和m的函数。满载时,m为定值,根据设计要求的偏频n可确定悬架初始角度θ0;变簧载时,则可根据m的值来调节θ0实现悬架的等偏频。 由图7可知,该仿生悬架不同初始角度对应不同的弹性特性和刚度特性曲线,本文根据簧载质量调节未受载时的初始角度θ0来改变悬架刚度,实现悬架等偏频等高度。该悬架采用初始角度自动调节装置(如气动人工肌肉、电动液压杆、气动杆等)代替图1中仿生悬架肌肉力发生器来调节未受载时的初始角度θ0,并随悬架运动。为了研究方便,本文假设初始角度自动调节装置的随动延迟为0。 由式(18)可得不同簧载质量与初始角度的关系: (20) 由式(20)可知,对于不同车辆不同的设计要求,确定刚度比后,每个偏频都对应一条簧载质量m、初始角度θ0和刚度k1取值关系曲线,图8为偏频1.8 Hz时的关系曲线。 图8 偏频为1.8 Hz时簧载质量、初始角度与刚度的取值对应关系Fig.8 Corresponding relationship between sprung mass, initial angle and stiffness at a partial frequency of 1.8 Hz 由图8可知,在实际设计中,可根据最大簧载质量m确定刚度k1范围,然后根据不同的刚度k1选择悬架初始角度θ0的变化范围。 以某两轴微型货车为研究对象,后轴满载轴荷为992 kg,后轴空载轴荷为576 kg,满载静平衡时悬架高度为0.468 m,取偏频1.8 Hz,仿生足骨杆与地面的夹角为33.8°(截取袋鼠跳跃落地瞬间的视频资料,测量袋鼠落地瞬间足骨与地面的角度获得)。仿生足骨杆长度l经计算为0.21 m。为了提高车辆的稳定性,本文采用较高的纵置弹簧与横置弹簧刚度比,即取α=2。在设计中一般使动挠度所对应的载荷为3~4倍的满载静负荷[12],故k1取40 056 N/m2,k2取20 028 N/m2。本文的悬架设计参数如表1所示。 表1 仿生悬架设计参数Tab.1 Bionic suspension design parameters 由式(20)可得某微型货车初始角度与后轴单边簧载质量m1的匹配关系,如图9所示。 图9 初始角度与后轴单边簧载质量匹配关系Fig.9 Matching relationship between initial angle and single-side sprung mass of rear axle 由图9可知,空载时后轴单边簧载质量为288 kg,满载时后轴单边簧载质量为496 kg,仿生悬架静平衡高度为0.468 m时,仿生悬架等偏频等高度设计的初始角度变化范围为51.5°~58.5°。在实际工作时,初始角度调节装置以空载为基准,根据计算所得θ0变化所需力的大小进行调节。 由式(18)可得某微型货车单边簧载质量m1变化时的偏频曲线,如图10所示。由图10可知,该微型货车从空载到满载连续载荷变化下,根据图9中的初始角度与质量匹配关系调节悬架的初始角度,可实现悬架静平衡时偏频始终为1.8 Hz。 图10 簧载质量连续变化下的偏频曲线Fig.10 Partial frequency curve under continuous change of sprung mass 以满载时后轴单边簧载质量496 kg为例,阻尼系数c1取800~2400 N·s/m,阻尼系数c2取400~1200 N·s/m时[19-21],根据仿生悬架的动力学方程[17],在MATLAB/Simulink中进行仿真试算,结果如表2所示。 表2 仿生悬架不同阻尼系数仿真结果Tab.2 Simulation results of different damping coefficients of bionic suspension 由表2可知,c1由800 N·s/m逐渐增大到1600 N·s/m时车身垂向加速度均方根值逐渐减小,由1600 N·s/m增大到2400 N·s/m时车身垂向加速度均方根值逐渐增大,在1600 N·s/m时为最小值,故本文c1、c2分别取1600 N·s/m和800 N·s/m。至此,仿生悬架偏频1.8 Hz时的相关设计参数取值均已获得。 以2.2节中微型货车为例,空载时后轴单边簧载质量为288 kg(后轴轴荷占比50%),半载时为385 kg(后轴轴荷占比55%),工况为:①B级路面,车速为40 km/h、60 km/h、80 km/h、100 km/h;②C级路面,车速为40 km/h、60 km/h、80 km/h;③D级路面,车速为40 km/h、60 km/h;④E级路面,车速为40 km/h。在这4种工况下进行等偏频等高度设计前后的参数特性仿真分析。因篇幅有限,仿真结果仅给出部分数据,如图11~图13和表3所示。 (a)空载、C级路面、车速60 km/h (b)半载、C级路面、车速60 km/h图11 等偏频等高度设计前后车身垂向加速度时域响应Fig.11 Time-domain response of vehicle body vertical acceleration before and after the constant partial frequency and constant height design (a)空载、C级路面、车速60 km/h (b)半载、C级路面、车速60 km/h图12 等偏频等高度设计前后车身垂向加速度频域响应Fig.12 Frequency domain response of vertical acceleration of vehicle body before and after the constant partial frequency and constant height design 图13 不同路面等级车身垂向加速度均方根值改善率Fig.13 The root mean square improvement rate of the vertical acceleration of the vehicle body on different road grades 表3 等偏频等高度仿生悬架仿真结果Tab.3 Simulation results of constant partial frequency and constant height bionic suspension 图11、图12所示为C级路面、车速60 km/h,空载和半载下等偏频等高度设计前后的车身垂向加速度时域和频域对比。由图11可知,等偏频等高度设计前空载车身垂向加速度范围为-2.55~2.37 m/s2,设计后在-2.05~1.55 m/s2之间,最大车身垂向加速度减小34.6%;等偏频等高度设计前半载车身垂向加速度范围在-1.71~1.39 m/s2之间,设计后范围为-1.41~1.19 m/s2,最大车身垂向加速度减小17.5%。该结果表明等偏频等高度设计可有效减小空载、半载车身垂向加速度峰值;相同路面等级相同车速下,等偏频等高度设计后,空载车身垂向加速度峰值较半载车身垂向加速度峰值降幅更大。 图12为图11的快速傅里叶变换,由图12可知,等偏频等高度设计后,车身垂向加速度响应峰值位置相对设计前向左偏移,空载和半载工况均处于1.8 Hz和20 Hz附近。空载工况下,设计前车身垂向加速度幅值谱最大值为0.245 m/s,设计后最大值为0.208 m/s,减小了15.1%;半载工况下,设计前最大值为0.190 m/s,设计后最大值为0.167 m/s,减小了12.1%。结果表明等偏频等高度设计有效改善了车辆频响特性。 由表3和图13可知:①随着车速的增大,不同路面等级空载和半载的车身垂向加速度均方根值改善率(即减小百分数)相对各级路面均呈现先增后减趋势,车速60 km/h时改善率最高,如B级空载改善率为15%,空载改善率(13.4%~15%)高于半载改善率(9.3%~11.9%),但它们均随车速的增大趋于稳定,结果表明等偏频等高度设计可有效改善车辆空载、半载的平顺性且改善效果随车速增大趋于稳定;②随着路面等级和车速的增大,空载悬架动挠度均方根值变化范围为0.16~1.52 mm,半载变化变化范围为0.02~0.06 mm,该结果表明,等偏频等高度设计前后的悬架动行程变化量小,对悬架的空间布置和尺寸设计影响不大;③随着路面等级和车速的增大,空载和半载的轮胎动位移均方根值变化量均呈现递增趋势,空载变化量(0.09~0.53 mm)大于半载变化量(0.01~0.06 mm),该结果表明,等偏频等高度设计后,车辆空载和半载的操纵稳定性略有下降,但变化量很小,车辆的操纵稳定性基本保持不变。 由上述分析可知,基于仿生悬架特性的等偏频等高度设计可有效改善商用车变簧载时的平顺性,但相对原仿生悬架,其悬架动挠度均方根值和轮胎动位移均方根值小幅增加,主要原因是仿生悬架被动工作时难以同时满足其平顺性和操纵稳定性最优的要求,文献[22]也有类似现象。 前期研究发现,仿生悬架比传统悬架具有更好的平顺性和操纵稳定性,悬架动挠度均方根值和轮胎动位移均方根值分别减小了71.5%和37.2%[17]。等偏频等高度设计后,相对于原仿生悬架,悬架动挠度均方根值增大0.2%~4.4%,轮胎动位移均方根值增大0.38%~5.59%,但增大量较小,对车辆操纵稳定性、悬架布置及尺寸设计影响不大。该结果验证了本文研究思路的正确性和方法的可行性。 悬架在实际工作中受路面激励影响,其刚度和偏频不能始终保持在设计值。为研究该影响,以2.2节中微型货车为例,对设计优化前后悬架空载和半载工况下的刚度、偏频变化进行分析。 当初始角度θ0、杆长l、纵置弹簧刚度k1、横置弹簧刚度k2和簧载质量m一定时,由式(18)可得悬架在实际工作中的刚度和偏频。空载和半载工况下,等偏频等高度设计前后的实际刚度和偏频随悬架动行程的变化如图14所示。 (a)刚度变化 (b)偏频变化图14 设计优化前后悬架实际工作中刚度和偏频变化曲线Fig.14 The stiffness and partial frequency curves before and after design optimization 由图14和表4可知,空载和半载工况下,等偏频等高度设计优化后较优化前刚度和偏频均明显减小,且在工作过程中变化范围更小,确保了悬架等偏频等高度工作的稳定性。 表4设计优化前后设计参数和刚度、偏频的差异Tab.4 Differences in design parameters, stiffness andpartial frequency before and after design optimization 为了与现有传统悬架进行特性对比,选择了文献[23]中偏频为1.6 Hz的变刚度螺旋弹簧悬架,在64 km/h和相同路面等级下,分别在空载343 kg、半载478 kg和满载612 kg情况下进行仿真对比,结果如表5所示。 表5 仿生悬架与传统悬架仿真结果对比Tab.5 Comparison of simulation results between bionic suspension and traditional suspension 由表5可知,在相同路面等级、相同车速下,仿生悬架车身垂向加速度均方根明显小于传统悬架车身垂向加速度均方根,如D级路面,在空载、半载和满载工况下,仿生悬架车身垂向加速度均方根较传统悬架分别减小43.7%、49.3%和57.1%。该结果表明仿生悬架的响应明显优于传统悬架,验证了仿生悬架等偏频等高度设计的合理性和有效性。 为进一步验证商用车等偏频等高度设计方案的正确性和有效性,搭建仿生悬架实验测试模型(图15),采用加速度传感器对不同路面条件下仿生悬架的垂向加速度进行测试,实验路面如图16所示。因条件有限,仿生悬架实验测试时,初始角度自动调节功能由多根不同刚度的角度调节弹簧实现。仿生悬架变簧载时等偏频等高度实验结果如表6所示。 图15 仿生悬架实验测试模型Fig.15 Bionic suspension experimental test model (a)路面1 (b)路面2 (c)路面3图16 实验路面Fig.16 Experimental pavement 表6 仿生悬架等偏频等高度实验结果Tab.6 Experimental results of the bionic suspension with the constant partial frequency and constant height 由表6可知,等偏频等高度设计后,不同路面条件下,半载测试模型垂向加速度均方根值较设计前改善率为12.1%~20.4%,空载改善率为20.6%~28.3%。该结果表明等偏频等高度设计有效减小了仿生悬架实验测试模型空载、半载的加速度均方根,进一步验证了等偏频等高度设计方案的正确性和有效性。 为追寻一种低成本、高品质商用车悬架,本文对双菱形仿袋鼠悬架进行了变簧载条件下的等偏频等高度设计,并开展特性研究,得到以下结论。 (1)仿生悬架具有较理想的弹性特性和刚度特性,比线性悬架有更多的动容量,更强的抗击穿能力。工程应用时,可根据应用对象的具体要求,选择合适的初始角度和刚度比来满足悬架设计要求。 (2)不同载荷下,仿生悬架通过调整初始角度使每一个载荷对应一条弹性特性曲线,实现等偏频等高度设计,验证了等偏频等高度设计方案的可行性。 (3)等偏频等高度设计可有效改善商用车变簧载时的平顺性。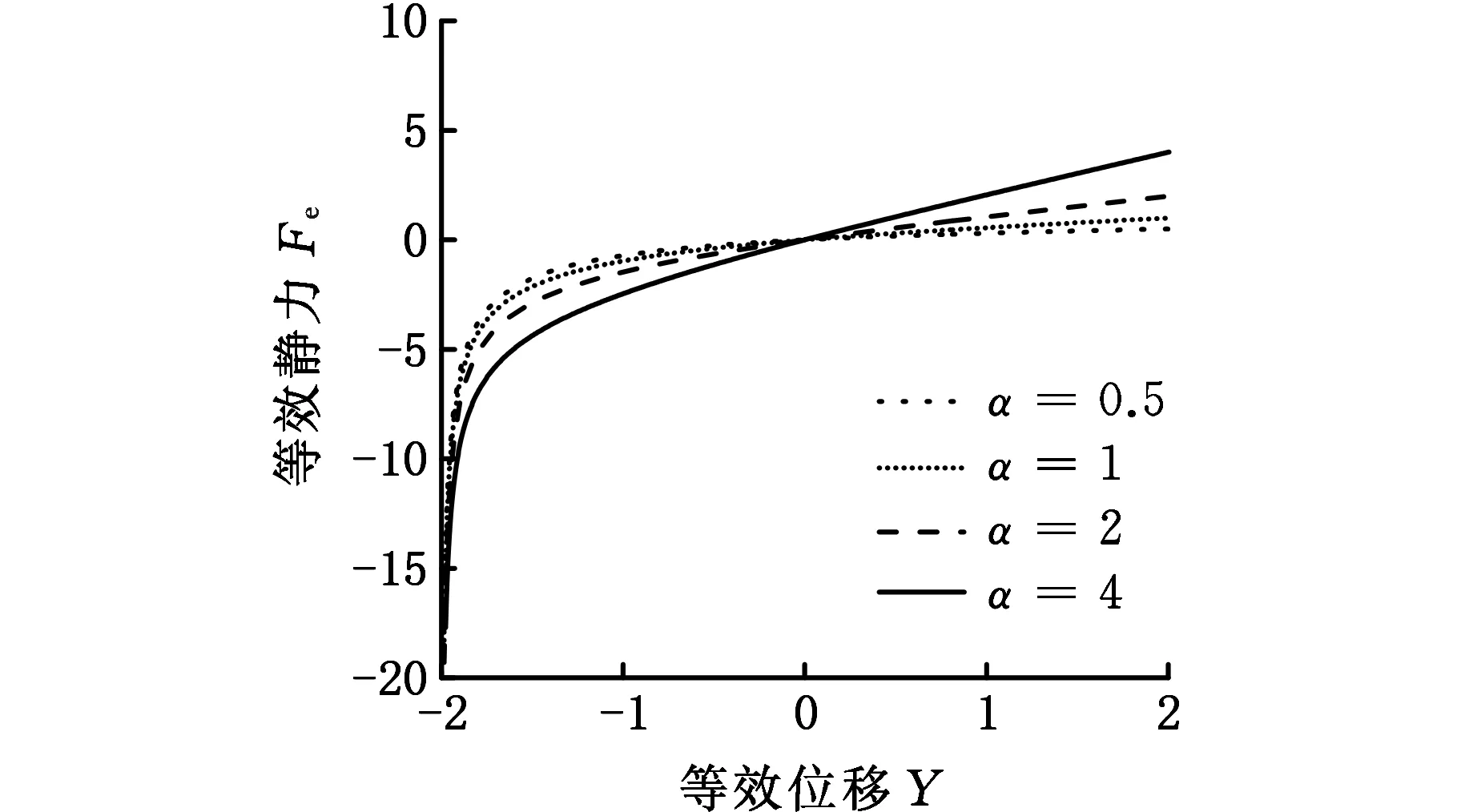


1.4 等偏频等高度设计理论
2 等偏频等高度设计方案与设计实例
2.1 等偏频等高度设计方案

2.2 等偏频等高度设计实例




3 等偏频等高度设计仿真分析
3.1 随机路面仿真分析





3.2 设计优化前后悬架刚度偏频变化分析


3.3 与传统悬架对比分析
4 实验验证



5 结论

