蒸汽管网运行数据监控方法研究

黄 赢

(南宁学院 信息工程学院，广西 南宁 530200)

1 统计过程控制的基本理论

统计过程控制(Statistical Process Control，SPC)是应用统计分析技术对过程中的各阶段进行评估和监控，发现异常并报警，管理工作人员会根据报警情况采取对应措施，从而消除异常，以达到提高和控制产品质量的目的[1]。在制造生产过程中，过程数据经常会产生波动，波动的因素有系统设备本身因素和外界因素。根据波动因素的不同，过程波动一般可以分为正常波动和异常波动。正常波动是由普通因素引起的，它具有偶然性和统计规律性，对生产过程数据影响小，可以忽略。异常波动是由系统本身因素造成，对过程数据的影响巨大，但是异常波动没有随机性，可以采取相应的措施消除异常波动带来的影响。

统计过程控制的目的就是使正常波动在正常合理的水平之上波动，能够对异常波动进行数据监控，及时发现异常波动并消除，从而满足生产需要，达到产品的质量标准。

2 统计过程控制图

1924年,美国休哈特博士第一次提出了控制图。控制图是过程控制的基本工具，能及时观察是否有正常波动和异常波动的存在，判断生产过程是否处于受控状态，监控生产过程的参数变化[2]，是使生产过程保持正常的有效工具。自休哈特控制图应用于过程变化监控领域以来，以休哈特控制图为基础不断有成熟的控制图相继提出。但是目前休哈特控制图仍被认为是监测过程变化和偏移的有效工具，休哈特控制图相对比较简单，在实际应用中大多数的过程观测数据近似服从正态分布。

休哈特控制如图1所示，由横坐标、纵坐标与3条控制线组成。横坐标为采样时间，纵坐标是质量属性值。控制限分别为中心线CL，控制上限UCL和控制下限LCL。当生产过程处于受控状态时，总体的质量特性数据服从正态分布。

休哈特控制图的基本原理就是利用3σ法则控制过程[3]，即控制上限确定为μ+3σ，控制下限确定为μ-3σ，中心限为μ，根据3σ原理，样本点落在控制限以外的概率仅为0.27%。这样确定好的控制极限可以以监控数据是否处于控制极限之内来判断生产过程是否处于受控状态。

控制图常常会发生两类错误，即虚发报警错误和漏发报警的错误，两类错误的具体分析如下：

(1)虚发报警错误。这种虚发报警的错误是指点子在生产系统处于正常运行的情况下，超出了控制极限，根据控制图的基本原理，点子超出控制极限则认为是生产过程失控，将进行报警，但是系统仍处于受控状态，这种错误称为虚发报警错误。虚发报警错误会产生查找不存在的异常因素的麻烦。

(2)漏发报警错误。在生产过程失控的情况下，质量特性值的分布与其典型分布发生了偏移，但是在上、下控制界限内总存在一部分质量特性值。如果在抽样检验时，正好抽到这部分产品，若样本点没有超出控制限即判断生产过程稳定就犯漏发报警的错误，这类错误的概率通常记为β。漏发报警将造成产品中次品率上升的损失。

根据统计过程控制对控制图的应用可知，控制上下限的确定是利用控制图进行过程控制的关键。确定合理的控制上下限可以有效地减少虚发报警错误和漏发报警错误发生的概率，若上限与下限的间距过大，则发生虚发报警错误的概率α减少，发生漏发报警错误的概率β增大，若上限与下限的间距过小，则发生虚发报警错误的概率α增加，发生漏发报警错误的概率β减少，所以无论上限与下限如何调整，两类错误发生的概率都会产生相应的变化，不可避免。所以确定上限与下限时要结合犯两类错误的总概率最小来确定。控制图的应用经验表明休哈特控制图采用的3σ方式使控制过程犯两类错误的总概率最小。

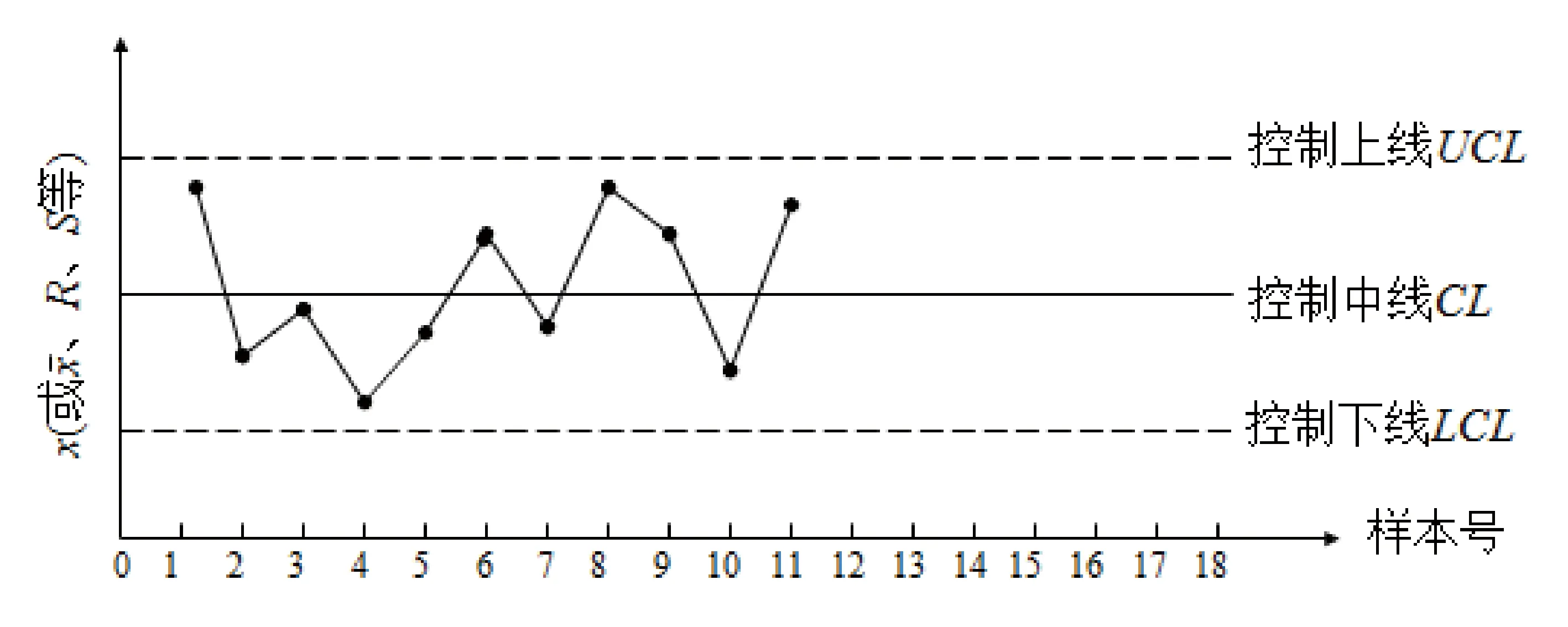
图1 休哈特控制图基本结构

控制图作为监控工具使生产过程处于受控状态，仅在随机因素的影响下运行。过程数据的分布曲线随时间的输出基本不发生变化且在要求范围内称为受控状态，反之称为失控状态，控制图可以通过对样本数据进行分析处理来判断这两种状态。生产管理人员根据控制图来判断生产是否处于正常状态，否则采取措施使之恢复正常，使生产过程保持稳定。

3 单变量统计过程控制在蒸汽管网运行数据监控中的应用

3.1 基于正态分布控制极限的确定方法

假设待观测的多变量系统的测量数据矩阵为X∈Rn,X=(x1,x2,x3,…,xn)，其中n为测量样本的个数，X为被测样本总体，X中的每一个元素为被测变量的一个样本，每个样本之间相互独立，则极差为：

R(x)=max(X)-min(X)

(1)

如果样本容量足够大，根据等距原则可以将极差R(X)分为N个小区间，用c代表每个区间，则每个小区间的长度：

(2)

这样就将该列数据矩阵分成N组，其中对应的每个小区间分别记为c1,c2,…,cn，矩阵X中的每一个样本数据都属于其中的一个区间。

统计采样值落入每个小区间的样本数占样本容量的百分比可表示如下：

(3)

其中，νr为落在该小区间的样本的个数，r=1,2,…N。

由于每个样本数值之间是相互独立的，根据统计概率的定义可知，每个区间，样本落入的概率为：

Pr{Xi∈cr}≈fr

(4)

则监测值落入每个区间的平均概率密度为：

(5)

由此，以平均概率密度Pr为高，以小区间的长度为底做矩形，得到直方图即为X的经验分布。当样本容量n区间个数N足够大时所得到的直方图就会更加接近X的总体概率的密度分布。

根据中心极限定理[4]：设均值为μ、方差为σ2(有限)的任意一个总体中抽取样本量为n的样本，当n充分大时，样本均值的抽样分布近似服从均值为μ、方差为σ2/n的正态分布，根据这个定理，当系统只存在一个稳定状态时，被测变量随样本容量的增大，趋向服从于正态分布。

当X服从正态分布时，根据正态分布理论可知其分布函数为：

(6)

如图2所示，当被监测的数据点处在μ±3σ的概率为99.73%，把控制极限设定在这个范围内，当所采集的数据点超出这个范围，则认为该数据异常，应该采取相应措施。

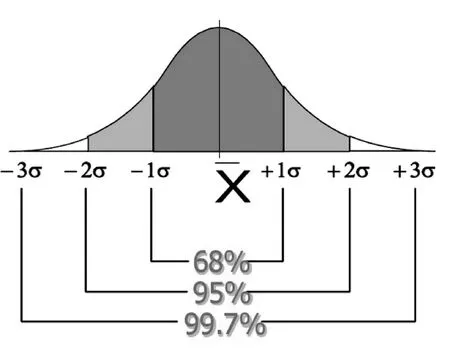
图2 标准正态分布概率密度分布

根据3σ原则，在实际生产中将监测数值点处在μ±3σ之外的0.27%的概率对应的区间定义为报警区，对应的区间值设为上上限和下下限，如果采集点超出这个范围则进行报警。将2σ点5%左右的概率定义为正常工作区，处在报警区和正常工作区之间的区间定义为调节工作区，正常工作区和调节工作区的界限点的值设为控制上限与控制下限。

在蒸汽管网流量监控中，当监控流量的样本容量和样本确定之后，由于系统因素，在取样的时间段内所采取的流量值可能会发生异常波动，从而使得到的经验分布不服从正态分布，在这样的情况下，通常可以采用正态分布拟合的方法来获得对应的正态分布和对应的控制极限，但是，这样拟合会产生非常大的误差，设定的控制极限也是均匀对称的，容易引起虚报或者漏报的情况。

3.2 基于经验分布的单变量控制极限的确定

(1)假设蒸汽管网监测某一变量X的上上限为Z1，则其满足的条件为：

P(X≥Z1)=0.13%

(7)

按照经验概率分布的划定标准可以写成：

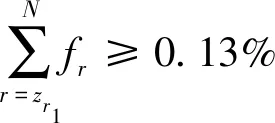
(8)

式中，rz1是Z1所在小区间中的序号，若统计区间分得足够细，则单个小区间的概率会很小，所以令该区间的控制上限或者控制下限定为Z1误差都很小，在这里取rz1区间的下限。

(2)假设蒸汽管网监测某一变量X的上限为Z2，则其满足的条件为：

P(X≥Z2)=2.5%

(9)

按照经验概率分布的划定标准可以写成：

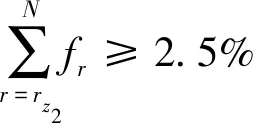
(10)

式中，rz2是Z2所在小区间中的序号，Z2取rz2区间的下限。

(3)假设蒸汽管网监测某一变量X的下限为Z3，则其满足的条件为：

P(X≥Z3)=2.5%

(11)

按照经验概率分布的划定标准可以写成：

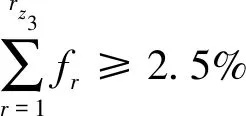
(12)

式中，rz3是Z3所在小区间中的序号，Z3取rz3区间的上限。

(4)假设蒸汽管网监测某一变量X的下下限为Z4，则其满足的条件为：

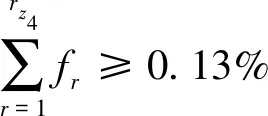
(13)

式中，rz4是Z4所在小区间中的序号，Z4取rz4区间的上限。

根据上面4步控制极限的划定可得到对应的报警控制极限，分别为控制上上限Z1、上限Z2、下限Z3、下下限Z4，确定极限时先划分区间，形成对应的经验分布函数，然后从r=1往上求和搜索，达到预定概率点的对应区间的序号，然后按照(1)～(4)确定相应的控制极限。

根据现场采集的数据，按人工设定的控制极限，按正态分布拟合设定的控制极限和按经验分布模型设定的控制极限对比如表1所示。

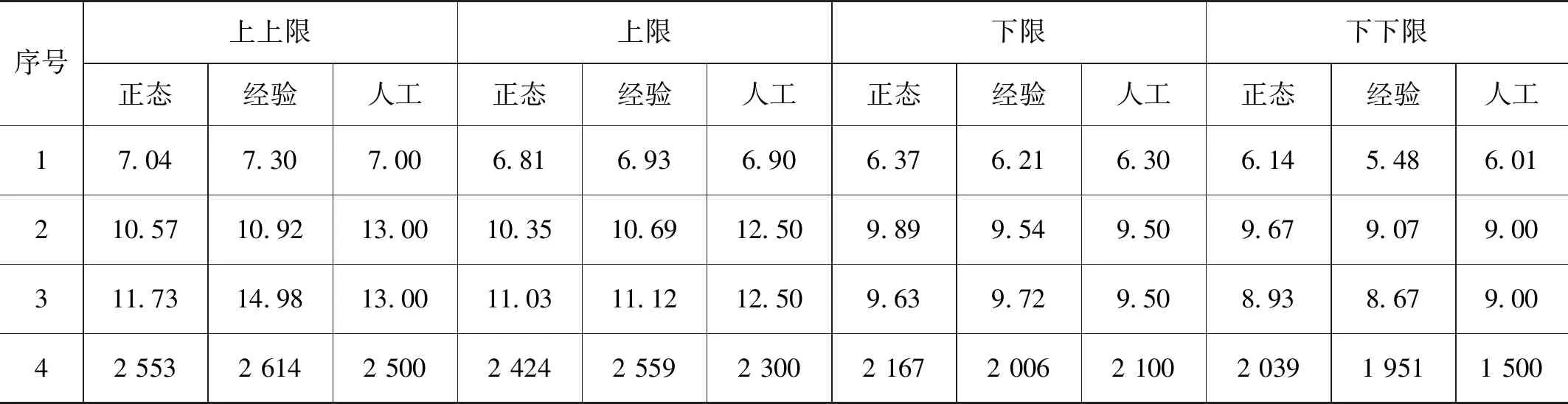
表1 3种方法确定的控制极限的对比

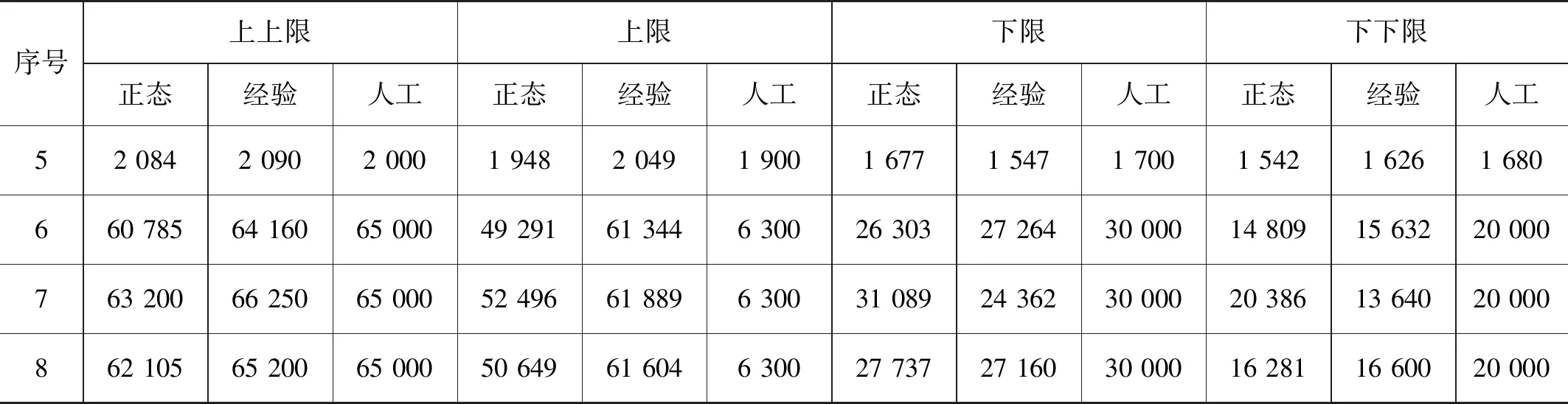
续表1

从表1中可以看出,采用正态分布、经验分布、人工设定的方法确定的控制极限都符合控制图的基本原理，样本点落在控制限以外的概率仅为0.27%，发生两类错误的总概率很小。而采用经验模型单变量控制极限的方法确定的极限中，上限加下限并不等于上上限加下下限，人工设定的控制极限也出现了同样的情况，而采用正态分布的方法确定的控制极限是对称的[5]。从数据来看，相对于采用正态分布的方法来确定控制极限，采用经验模型划定的控制极限与人工划定的控制极限值更为接近，比较符合实际生产情况。因此，采用经验分布来确定的控制极限值更精确，更符合生产需要。

4 结语

蒸汽管网流量数据监控主要利用单变量统计过程控制的方法。确定控制极限是本章研究的核心问题。针对单变量控制极限的问题，本文主要根据流量的历史数据，得到该流量数据的经验分布，最后再按照正态分布“3δ”原理定义的控制极限的对应概率，在经验分布中寻找与该概率对应的变量的取值，形成对应的控制极限。这种确定控制极限的方法是以数据统计的原理作为基础，划分出的控制极限并不对称，根据实验测试，这种控制极限的方法比采用经典的正态分布“3δ”原则得到的控制极限的方法更符合工艺与安全要求。

按本文确定控制极限的方法,运用单变量统计过程控制对蒸汽管网流量数据进行监控，监控效果表明，本章研究的方法能明确地对蒸汽管网异常数据给出明确的报警信号，起到了很好的监控效果。