“球槽模型”的压力极值位置分析

李旭斌

（中国人民大学附属中学朝阳学校，北京 100028）

球槽模型是高中物理的一类经典模型.在动量与能量综合的习题课教学中，教师经常以此模型为抓手，让学生推导钢球运动到最低点时的速度，以巩固动量守恒及机械能守恒的应用.笔者在执教过程中发现学生存在“钢球运动至最低点时对凹槽产生的压力最大”的前概念，为一探究竟，笔者查阅文献［1］，发现将钢球视为质点模型，可以通过数理解析得出只有当槽质量为钢球质量2.73倍以上时，钢球在最低点才有最大速度.为考虑更一般的情形，笔者尝试不将钢球视为质点，并结合了刚体纯滚动、柯尼希定理、伽利略变换等方面的竞赛知识做了深入思考.

1 问题的提出

如图1，半圆形凹槽静止放置在光滑水平地面上，钢球从半圆形凹槽的左侧边缘由静止释放，凹槽质量为M，钢球质量为m、半径为R，凹槽圆心到钢球球心的距离为r，重力加速度为g.

图1 半圆形凹槽板块模型

如果凹槽固定在地面上，钢球运动过程等价于“球绳模型”，钢球运动到最低处对凹槽产生的压力最大，但是当凹槽与地面不再固定，钢球仍然是在最低处对凹槽产生的压力最大吗？由于钢球向下纯滚动过程中，凹槽向左运动，两者相互挤压，压力最大位置有可能出现在最低点附近吗？

2 定量分析

如图2，钢球上行过程中，钢球相对于凹槽的质心速度vC′平行于凹槽切线方向斜向右上方，根据几何关系vC′与水平方向夹角为θ，此时凹槽获得水平向左的速度v.凹槽对钢球的支持力为N，钢球所受重力为G，钢球所受静摩擦力为f.

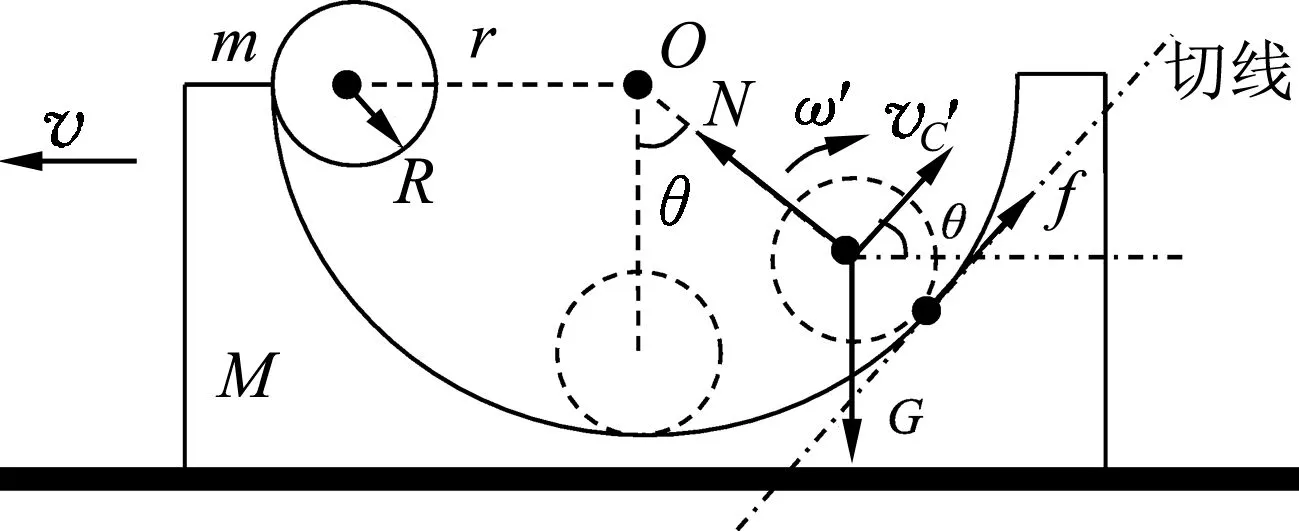
图2 钢球沿凹槽上行

根据伽利略变换可得此时钢球对地水平向右的速度为vC′cosθ＋v，根据水平方向动量守恒有

忽略滚动摩擦所产生的机械能损耗，以钢球在最低处球心所在平面为零势能面，从开始到图2状态，根据系统机械能守恒有

根据“柯尼希定理”钢球对地的总动能T为质心对地平动动能和钢球相对质心的转动动能之和，有

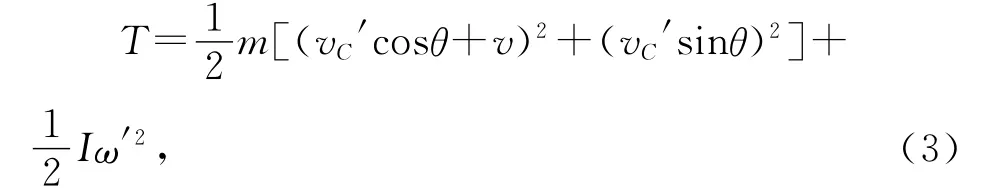
钢球上行过程中相对凹槽做纯滚动，有

球心相对O点做圆周运动，法线方向由牛顿第二定律可得

联立（1）－（5）式得到

笔者尝试同样运用数理解析，将（6）式对cosθ进行求导，令导数为0以求得钢球对凹槽压力的极值，以及压力极值出现的位置，但是过程繁琐且最终的方程为一元五次，难以求解，因此笔者决定采用计算机数值模拟的方法取代（6）式的数理解析求法进行分析.

2.1 情形1：M＞m，判断N max出现的最大位置

取M＝2 kg，m＝1 kg，R＝0.1 m，r＝1 m，g＝10 m／s2.采用 Mathematica软件绘制的图像如图3所示.

图3 M＞m情形下的压力大小随夹角θ的变化

通过图像可以发现，钢球对凹槽压力最大的位置在最低处，此时槽质量是钢球质量的2倍，在文献［1］中描述的槽质量是钢球质量的2.73倍以下，此时仍然得到钢球对凹槽压力极值出现在最低处，可见考虑钢球大小和外形的必要性.

2.2 情形2：M＝m，判断N max出现的最大位置

取M＝1 kg，m＝1 kg，R＝0.1 m，r＝1 m，g＝10 m／s2.采用 Mathematica软件绘制的图像如图4所示.

图4 M＝m情形下的压力大小随夹角θ的变化

通过图像可以发现，钢球对凹槽压力最大的位置在－0.3 rad到0.3 rad之间，由此发现槽质量等于钢球质量是压力极值偏离最低点的临界条件.

2.3 情形2：M＜m，判断N max出现的最大位置

取M＝1 kg，m＝2 kg，R＝0.1 m，r＝1 m，g＝10 m／s2.采用 Mathematica软件绘制的图像如图5所示.

图5 M＜m情形下的压力大小随夹角θ的变化

通过图像可以发现，钢球对凹槽压力最大的位置在－0.6 rad和0.6 rad处，此时最大压力出现的位置不再是最低处，而是在最低处附近的两个对称的位置上.

3 小结

考虑钢球的大小和外形，通过计算机数值分析发现，槽质量等于钢球质量是压力极值偏离最低位置的临界条件，当半圆形凹槽质量大于钢球质量时，钢球对凹槽的最大压力出现在最低处；当半圆形凹槽质量小于钢球质量时，钢球对凹槽的最大压力出现在最低处附近的两个对称的位置上.该结论与将钢球视为质点情形下的分析结果有所不同，并且考虑钢球的外形及钢球的滚动效应是必要的.

教师在面向物理资优生的教学中要注意将学生“钢球在最低点对凹槽压力最大”的前概念转化为“钢球质量小于凹槽质量时，钢球在最低点对凹槽压力最大”.可见，物理结论的成立存在一定的适用条件，当给定的条件、原有模型发生变化时，原有的物理结论也将发生变化，教师在日常教学中应注意引导学生关注物理结论成立的背景及条件，防止思维定式的产生.这也有利于前概念的转化.