基于畦田双侧灌水条件下灌水参数优化研究

高卓卓，郑志伟，豆静静

（天津农学院 水利工程学院，天津 300392）

地面灌溉是目前最普遍采用的灌溉技术之一，具有设备简单、成本低等优点[1-2]。但与喷灌、滴灌等精准节水灌溉技术相比，地面灌溉技术存在灌溉水利用率低、灌水时间长、易形成深层渗漏、造成地面冲刷、破坏土壤结构等问题[3]。因此探索灌溉水利用率高、灌水时间短的地面灌溉技术尤为必要。

畦灌是我国北方地区普遍应用的地面灌溉技术[4-6]。王明辉等[7]设计不同畦灌的畦长、畦宽、单宽流量及田面坡度等参数组合进行灌水试验，得到了灌水质量评价指标较高的灌水参数和畦田规格参数组合；张立志等[8]利用WinSRFR4.1模型模拟不同规格畦田的灌水过程，研究不同灌水技术参数组合对灌水质量的影响，得到了适合黄河下游引黄灌区的畦长、畦宽、坡度和单宽流量的灌溉方案；雷国庆等[9]以灌水效率与灌水均匀度之和为目标函数，建立了畦灌灌水技术参数的实用优化模型，提高了灌水质量。

灌水技术参数变化对灌水质量的影响较为复杂，并在实际灌水过程中，受地形限制等因素的影响[10-15]，有必要进行逆坡灌水。本研究针对上述问题，在天津市武清区崔黄口镇西吕村，设置畦首畦尾两泵同时灌水，在缩短一半灌水时长的同时，结合WinSRFR5.1模型[16-17]模拟地面灌水，分析评价灌水质量评价指标[18-19]，优化试验区灌水技术参数。

1 材料与方法

1.1 试验区基本情况

试验区位于天津市武清区崔黄口镇西吕村，畦田坡度为0.001 0，由南向北灌水。

1.2 模型介绍

WinSRFR5.1模型是以零惯量水流运动模型为基础，结合考斯加可夫入渗模型进行灌水技术参数优化和灌溉分析评价。

1.2.1 零惯量水流运动模型

零惯量水流运动模型是在非守恒型全水动力学模型基础上[20-21]，忽略了其模型的惯性项（即加速度项）[10]得出，该模型可以合理确定畦田规格和畦灌技术参数[22]，计算时间快，精度高，因此广泛用于研究畦灌水流运动。其基本方程为：

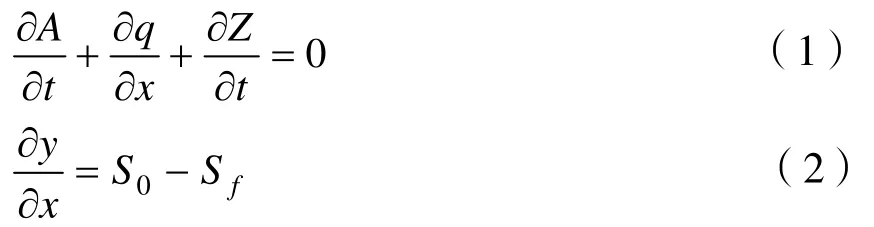
式中，A为地面水流断面面积，m2；q为地面水流的单宽流量，L/（s·m）；Z为土壤入渗量，mm；t为时间，min；x为距离，m；y为田面水深，m；S0为田面纵坡度；Sf为阻力坡度。

1.2.2 考斯加可夫入渗模型

考斯加可夫入渗模型[18]公式为：

式中，Z为t时间内累计入渗量，mm；K为入渗系数，第一个单位时间内的平均入渗率；t为入渗时间，min；α为入渗指数。

1.3 试验方法

选取本地区常见规格田块作为研究对象，试验田种植冬小麦，畦长160 m，畦宽7.5 m，测定灌前土壤含水率、地面坡度等参数，再利用WinSRFR5.1模型模拟地面灌水试验。田间试验于2018年3月30日进行，在北、南双侧同时开泵进行灌水试验（以下简称顺坡侧灌水和逆坡侧灌水）。以顺坡侧灌水为正方向，水流汇合点在85 m处，观测并记录关口时间、灌水量、单宽流量、灌水时间，并测量灌前灌后土壤含水率。

使用WinSRFR5.1模型的灌溉系统设计功能，将试验田以双侧水流汇合处为界划分为两块畦田进行模拟，对畦田规格和灌水技术参数进行优化，得到以畦长与畦宽为变量的灌溉性能等值线图。将逆坡侧灌水坡度近似设为0.000 1，使得灌溉水流形成均匀流进行模拟。

1.4 灌水质量评价指标

选用灌水效率（PAE）和灌水均匀度（DU），作为灌水质量评价指标[23-24]。

灌水效率（PAE）是指土壤根系活动层要求的储水量Wz与实际灌水总量Wapp之比，即灌溉水被植物利用的百分数，见公式（4）。

灌水均匀度（DU）是指灌水范围内田间土壤湿润的均匀程度，见公式（5）。

1.5 水流推进及消退数据拟合度检验

为确保WinSRFR5.1模型模拟的入渗参数更加准确，需对模拟及田间实测水流推进及消退数据进行拟合度检验，并通过反复模拟以减小模拟与实测结果的差异。模拟过程中采用均方根误差Re来评价模型的模拟效果，均方根误差方程见公式（6）。

式中，tTi为水流推进或消退到第i点（共n个点）所用时间的实测值，min；tSi为对应水流推进或消退到第i点所用时间的模拟值，min。

2 结果与分析

2.1 土壤入渗参数计算

利用水流推进与消退数据推求畦块双侧灌水土壤入渗参数（入渗参数K和入渗指数α）[6]。表1为推求出的畦块双侧灌水土壤入渗参数与田间基本数据。

表1 土壤入渗参数、田面糙率及田间基本数据

由图1可知，畦块双侧灌水水流推进、消退的实测曲线与模拟曲线的吻合程度均很高，顺坡侧灌水水流推进、消退数据实测值与模拟值均方根误差Re分别为0.09和0.07，逆坡侧灌水水流推进、消退数据实测值与模拟值均方根误差Re分别为0.05和0.08。说明该模型适用于畦块双侧灌水[10]，用此方法计算得到的入渗参数K和入渗指数α合理。

图1 畦块双侧灌水水流推进与消退的实测曲线与模拟曲线

进一步对基于 WinSRFR5.1模型优化模拟获得的土壤入渗参数值（即模拟值）的准确性进行验证，通过计算相对误差对模拟值及根据公式（3）计算获得的土壤入渗参数值（即计算值）进行检验。由表2可知，入渗系数K和入渗指数α计算值与模拟值相对误差最大值分别为 3.23%和3.64%，由此说明，根据WinSRFR5.1模型所优化的土壤入渗参数值准确可靠。

表2 土壤入渗参数计算值与模拟值相对误差

2.2 灌水质量等值线图分析

图2为WinSRFR5.1灌溉系统设计模块输出的顺坡侧灌水畦长、畦宽与PAE和DU等值线图。

图2 顺坡侧灌水灌水效率和灌水均匀度重合等值线图

由图2可知，PAE与DU具有较高的吻合度。当畦长在一定范围内，单宽流量一定时，随着畦宽的增大，PAE和DU先增大后减小；畦宽在一定范围内，随着畦长的增大，PAE和DU均逐渐减小。当畦长小于24 m时，PAE和DU受畦宽变化的影响不大。当畦长在24～54 m时，随着畦宽的增大，PAE和DU先增大后减小，并在畦宽为2.4～10 m时达到峰值。当畦长大于54 m时，随着畦长增大，满足PAE和DU达到80%以上的畦宽逐渐减小，且最大畦宽为6 m。

图3为WinSRFR5.1灌溉系统设计模块输出的逆坡侧灌水畦长、畦宽与PAE和DU重合等值线图。

由图3可知，单宽流量一定时，畦长不变，随着畦宽的增大，PAE和DU均逐渐减小；畦宽不变，随着畦长的增大，PAE和DU逐渐减小[15]。当畦长小于27 m时，PAE和DU受畦宽变化的影响不大；当畦长大于27 m时，畦宽与畦长呈反比例关系，当PAE和DU达到80%以上时，畦宽随畦长的增大而逐渐减小。

图3 逆坡侧灌水灌水效率和灌水均匀度重合等值线图

由图2、图3对比可知，选取图2中PAE和DU均达到95%的部分，且畦宽为2.0～11.5 m时，PAE和DU在90%以上的顺坡侧灌水畦长范围为32～100 m，逆坡侧灌水畦长范围为17～65 m。

3 结论

（1）畦块双侧灌水水流推进、消退过程的模拟值与实测值拟合度较高，顺坡侧灌水水流推进、消退数据实测值和模拟值均方根误差Re分别为0.09、0.07，逆坡侧灌水水流推进、消退数据实测值与模拟值均方根误差Re分别为0.05、0.08。入渗系数K和入渗指数α计算值与模拟值相对误差最大值分别为3.23%和3.64%，即基于WinSRFR5.1模型优化得到的土壤入渗参数值准确性较高。

（2）根据模拟可得，顺坡侧灌水时，当畦长小于24 m时，PAE和DU受畦宽变化的影响不大；当畦长在24～54 m，畦宽为2.4～10.0 m时，PAE和DU达到95%；当畦长大于54 m时，PAE和DU达到80%的最大畦宽为6 m。逆坡侧灌水时，畦长小于27 m时，PAE和DU受畦宽增大的影响不大；当畦长大于27 m时，畦宽与畦长呈反比例关系，满足PAE和DU均大于80%的畦宽随畦长的增大而逐渐减小。

（3）在提高灌水质量的前提下，结合天津市武清区畦田现状，得到适合畦块双侧灌水畦田的畦长、畦宽范围，即：畦宽为2.0～11.5 m，畦长为49～165 m时，PAE和DU均达到90%以上。