Sprott B超混沌系统比例积分滑模同步五个方案
杨喜平,毛北行
(郑州航空工业管理学院 数学学院,河南 郑州 450046)
1 引 言
混沌系统同步自提出以来就备受关注,其中非线性系统的同步已成为研究的热点。学者们提出了各种各样的混沌系统,例如:Chen 系统、Lorenz 系统、Liu系统、Sprott混沌系统等[1-2],也尝试了多种方法来研究混沌系统的同步控制。其中利用滑模方法研究非线性系统的同步已经取得了很多成果,例如文献[3-4]提出了滑模新方法,文献[5]研究了纠缠混沌系统的比例积分滑模同步问题,文献[6]研究了分数阶时滞金融混沌系统的同步控制,文献[7-8]研究混沌系统的指数同步。另一方面,Sprott混沌系统的同步引起了学者们的高度关注,例如文献[9-10]研究了Sprott混沌系统同步与控制,文献[11]研究了不确定Sprott-D 混沌系统的有限时间鲁棒反馈控制,文献[12]研究了一个新的未知参数Sprott超混沌系统的自适应同步。在以上研究的基础上,本文基于比例积分滑模方法研究了Sprott B超混沌系统的滑模同步问题的五种控制方案。
2 系统描述
Sprott B超混沌系统[12]
(1)
当a=0.2,初始值设置为(x1(0),x2(0),x3(0),x4(0),x5(0))=(0.05,0.05,0.05,0.05,0.05)时,系统(1)的Lyapunov指数分别为λ1=0.386,λ2=0.040,λ3=0,λ4=-0.030,λ5=-0.415。

3 控制方案
3.1控制方案一
以系统(1)为主系统,设计从系统为
(2)
定义误差ei=yi-xi(i=1,2…5),得到
(3)
假设1 |y2e3|+|x3e2|+|e5|<λ|e1|,且y2,x3非零,其中λ为正常数。
定理1 在假设1条件下,设计滑模面
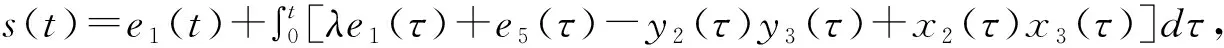



根据引理1,可以推得s→0。
3.2控制方案二
以系统(1)为主系统,设计从系统为
(4)
定义误差ei=yi-xi(i=1,2,…,5),得到
(5)



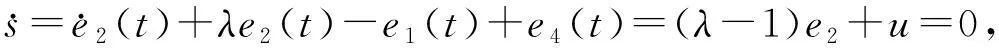


3.3控制方案三
以系统(1)为主系统,设计从系统为
(6)
定义误差ei=yi-xi(i=1,2,…,5),得到
(7)
假设3 |x1e2|+|y2e1|<λ|e3|,其中λ为正常数。
定理3 在假设3条件下,设计滑模面
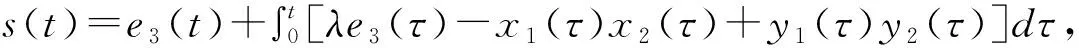



3.4控制方案四
以系统(1)为主系统,设计从系统为

(8)
定义误差ei=yi-xi,得到
(9)

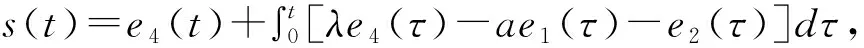

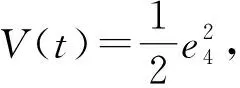
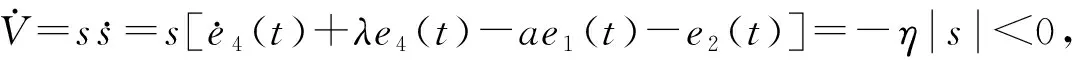
3.5控制方案五
以系统(1)为主系统,设计从系统为
(10)
定义误差ei=yi-xi(i=1,2,…,5),得到
(11)
假设5 |e1|<λ|e5|,|e4|<|e2|,且y2非零,其中λ为正常数。



4 数值仿真
当a=0.2,初始值设置为(x1(0),x2(0),x3(0),x4(0),x5(0))=(0.05,0.05,0.05,0.05,0.05)时,系统出现奇怪吸引子,定理(1-5)中参数λ,η的取值分别为λ=2.0,1.5,1.5,1.5,1.5,η=3,2.5,2.5,3.2。由定理(1-5)的比较可看出,结论成立的条件逐渐放宽,同步效果越来越好,取得同步的时间也越来越短。记定理(1-5)所需的同步时间分别为T1,T2,T3,T4,T5,彼此之间的大小关系为T1>T2>T3>T4>T5,而设计的比例积分滑模函数逐渐由复杂趋于简单,对控制器的要求也逐渐由强变弱,控制效果逐渐由坏变好。另外,从构造的比例积分滑模函数和对假设条件的要求上看,误差方程越简单,可以构造出更简便的滑模面,假设条件也更宽松。
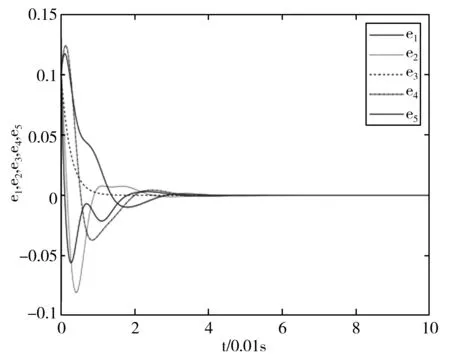
图1 定理1中误差
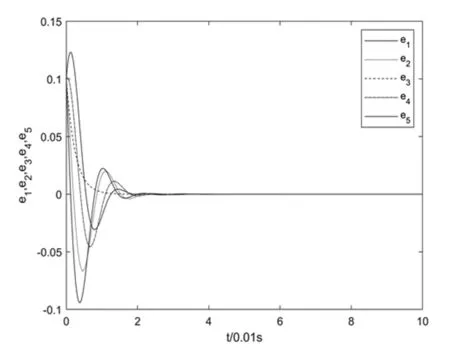
图2 定理2中误差

图3 定理3中误差
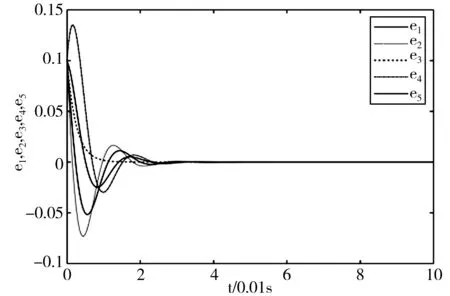
图4 定理4中误差

图5 定理5中的系统误差曲线
5 结 论
根据稳定性理论和混沌同步相关理论,结合积分滑模处理非线性系统的方法研究了Sprott B超混沌系统比例积分滑模同步的五个控制方案,得到了Sprott B超混沌系统的主从系统取得比例积分滑模同步的五个充分条件,从数学角度给出了严密的逻辑证明过程,并通过MATLAB仿真验证了方法的正确性。文中使用的比例积分滑模方法对整数阶系统、分数阶系统都有很好的实用性,可以用来解决很多非线性混沌系统的同步问题。

