指数形式的二次相关GCC-PHAT-β时延估计算法

李皖婷， 李登峰， 张修靖， 张天婷， 黄杉杉

(长安大学电子与控制工程学院， 西安 710064)

声源定位是以时延值已知与声速已知作为前提条件，以时间与速度的关系式计算声源到不同声传感器之间的距离[1]，通过多元十字阵列计算得到目标声源的俯仰角、方位角和距离等位置信息[2]。由于多元十字阵列的几何特性，在对声源进行定位的过程中时延值估计的误差被放大，使定位误差也随之增大[3]。因此如何降低在时延估计过程中的误差对提高声源定位的准确度具有重要意义。

在对时延值进行估计时，前期普遍使用的基本互相关算法具有峰值不凸出导致时延估计误差较大等明显的缺陷；为了弥补互相关算法的不足，前人在原有算法的基础上引入了加权函数的概念后得到了广义互相关算法，文献[4]在相位变换(phrase transform，PHAT)加权函数的广义互相关算法的基础上，将算法的加权函数与相关噪声的互功率谱相减，再根据信噪比的不同赋予其不同的权值，并添加一个相干函数来构造一种新的加权函数的时延估计算法，该算法在信噪比为0 dB以上时能有效地抑制噪声而凸出峰值, 降低了时延值在估计过程中的误差，但并没有对信噪比在0 dB以下时的峰值凸出情况进行说明；文献[5]基于广义平滑相干变换(smooth coherent transform，SCOT)算法和广义HB算法，提出了一种SCOT-HB复合加权广义互相关算法，在加权函数的分子项中加入模平方相干函数来提高信号中高信噪比部分的能量并抑制低信噪比部分的能量，在信噪比不高于0 dB时减少了时延估计过程中的计算量，而且提升了时延估计的稳定性和正确率，但该算法并没有对0 dB以下时的峰值凸出和时延估计情况进行解释说明；文献[6]将最小平均P范数与加权函数相结合，提出了一种基于最小平均P范数的时延估计算法，该算法在非高斯环境下具有能有效抑制谐波、收敛性强、时延估计精度高和迭代速度快等优点，但当其受到的噪声信号强度大于语音信号强度时该算法的时延估计精度降低。文献[7] 基于高阶累积量和二次相关算法，提出了一种结合希尔伯特变换方法的时延估计算法，该算法使得峰值更加凸出，均方根误差更低且能获得更高的时延估计精度，但在2 dB以下的信噪比时算法失效。

针对上述问题，现提出一种应用在低信噪比条件下的指数形式的广义二次相关算法。首先，以已有广义二次相关算法为基础，将获得的功率谱函数进行傅里叶逆变换后，对结果进行指数运算,得到改进算法；然后在由软件构造的加有高斯白噪声的两路单频正弦波信号，分别在不同信噪比下对广义互相关算法、广义二次相关算法和改进算法进行实验仿真，验证在低信噪比下峰值较凸出的时延估计算法；最后选用一段男声音频作为信号源，比较3种算法在进行时延估计时所产生的误差大小，获得在-10～10 dB低信噪比范围内的较优算法。

1 时延估计算法

1.1 基本互相关时延估计算法

设声传感器M1和M2接收到的信号分别为x1(t)和x2(t)，假定噪声n1(t)与n2(t)为互不相关的高斯白噪声，且噪声和声源信号s(t)之间也互不相关，表达式为

x1(t)=α1s(t-τ1)+n1(t)

(1)

x2(t)=α2s(t-τ2)+n2(t)

(2)

式中：α1和α2分别为声源s(t)传播到M1和M2后的衰减系数；τ1和τ2分别为声源s(t)到达声传感器M1和M2所需要的时间。则以τ=τ1-τ2来表达声传感器M1和M2接收到声源信号的时间差，即为时延值。两路信号x1(t)、x2(t)的互相关函数R12(τ)可表示为

R12(τ)=E[x1(t)x2(t-τ)]

(3)

将式(1)、式(2)代入式(3)，可得

R12(τ)=α1α2E[s(t-τ1)s(t-τ2-τ)]+

α1E[s(t-τ1)n2(t-τ)]+

α2E[n1(t)s(t-τ2-τ)]+

E[n1(t)n2(t-τ)]

(4)

由于假定高斯白噪声n1(t)、n2(t)互不相关，且噪声n1(t)、n2(t)和声源信号s(t)也互不相关，因此式(4)可表达为

R12(τ)=α1α2E[s(t-τ1)s(t-τ2-τ)]

=α1α2Rss[τ-(τ1-τ2)]

(5)

由自相关函数的性质可知：当τ-(τ1-τ2)=0，即τ=τ1-τ2时，R12(τ)值取最大[8]。因此信号x1(t)和x2(t)之间的时延可表示为

(6)

由上述可知，时延可由目标声源到达两个声传感器之间信号所构成的互相关函数来获得[9]。是以要获得准确的时延值，就必须准确求解出互相关函数的最大值，这就要使其最大峰值十分凸出，但是在互相关函数的计算中，以两个高斯白噪声互不相关和高斯白噪声与声源互不相关为前提条件，该结论才会顺利得出。然而现实环境中充斥着大量噪声，假设难以实现，所以由基本互相关时延估计算法得到的函数图形中，其峰值最大处并不凸出，因此准确计算出时延值极其艰难。

1.2 GCC-PHAT-β时延估计算法

广义互相关(generalized cross-correlation phrase transformation-β，GCC-PHAT-β)算法[5]是对基本互相关算法加以改进而得到的算法，将加权函数乘以由两路信号进行傅里叶变换得到功率谱函数[1]，使其达到增强抗噪性能的目的并使对时延进行估计时的误差降低。

设声传感器M1和M2接收到的信号分别为x1(t)和x2(t)，假定噪声n1(t)与n2(t)为互不相关的高斯白噪声，且噪声和声源信号之间也互不相关。

x1(t)=α1s(t)+n1(t)

(7)

x2(t)=α2s(t-τ)+n2(t)

(8)

式中：τ为声源到达声传感器M1、M2之间的时延。则两路信号x1(t)、x2(t)所构成的Rx1x2(τ)为

(9)

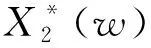
将函数Rx1x2(τ)经傅里叶逆变换从频域转换到时域，检测最大峰值并对其进行时延估计。其算法的原理图如图1所示。选取的加权函数各有差异，算法的公式组成也各有不同，如表1所示。在现实应用中，加权函数的选取还需随着具体应用场景的改变而改变[10]，使傅里叶逆变换后的函数最大峰值更为凸出，以便得到高精度的时延值。

图1 广义互相关算法原理图Fig.1 Schematic diagram of generalized cross-correlation algorithm

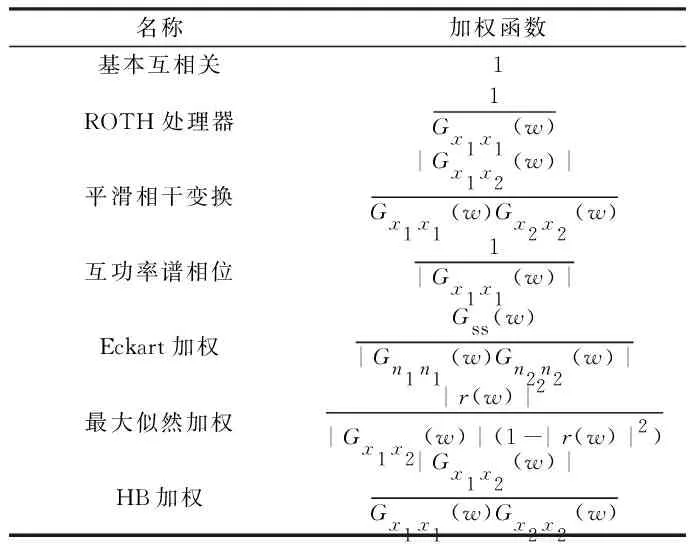
表1 常用的几种加权函数Table 1 Several commonly used weighting functions

|r(w)|2表达式为

(10)

当处在信噪比较低的环境中或对多个目标声源进行定位时，噪声与声源之间叠加或多个声源叠加产生的问题严重影响着GCC-PHAT-β算法进行时延估计时的性能；反之当处在信噪比较低的环境中并对单个目标声源进行定位时，GCC-PHAT-β算法和基本互相关算法相比易达成且时延估计造成的误差较低[5]。总而言之，在较低信噪比的环境中，GCC-PHAT-β算法对单个目标声源进行定位时的性能方面和误差方面都强于基本互相关算法。

1.3 改进的二次相关GCC-PHAT-β时延估计算法

1.3.1 二次相关时延估计算法

为了增强基本互相关算法在进行时延估计时的抗噪性能，在其基础上进行完善后取得二次相关算法来有效降低时延估计过程中信噪比下降时噪声占据比例较大对时延估计性能的影响。

x1(t)的自相关函数为

R11(τ)=E[x1(t)x1(t-τ)]

=α1α1Rss+α1Rsn1+α1Rn1s+Rn1n1

(11)

x1(t)和x2(t)的互相关函数为

R12(τ)=E[x1(t)x2(t-τ)]

=α1α2Rss+α1Rsn2+α2Rsn1+Rn1n2

(12)

此时R11(τ)与R12(τ)仍是以时间τ为因变量的函数，对这两个函数进行第二次互相关运算，取得二次相关函数RRR(τ)为

RRR(τ)=E[R11(τ)R12(t-τ)]

(13)

用式(11)、式(12)来表示式(13)，假定目标声源信号与噪声互不相关，则式(13)可表示为

RRR(τ)=RRS(τ-D)+RRN(τ)

(14)

式(14)中：RRS、RRN分别为声源、噪声的二次相关函数。假设噪声之间互不相关，则RRN=0。从式(14)中可知，在τ=D时，RRS(τ-D)获得最大值，即二次相关函数RRR(τ)获得最大值，则此时的τ就为所求的时延值。而在使用二次相关算法对时延值进行估计时，增加了先对一个声传感器接收到的声音信号施行自相关运算的步骤，以便增强算法的抗噪性能[11]。因此二次相关运算与GCC-PHAT-β算法在信噪比逐渐降低的条件下，二次相关算法更能进行有效的时延估计，其原理框图如图2所示。

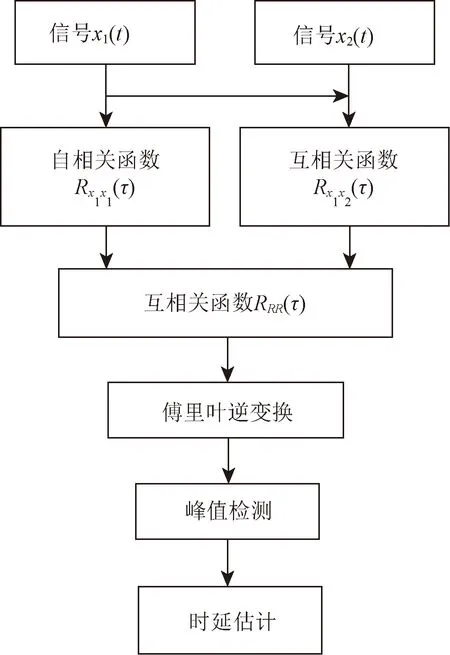
图2 二次相关算法流程图Fig.2 Quadratic correlation algorithm flowchart

1.3.2 二次相关GCC-PHAT-β时延估计算法

GCC-PHAT-β算法是将加权函数乘以由两路信号进行傅里叶变换得到功率谱函数，使其算法的抗噪性能得到加强，并使对时延进行估计时的误差降低，是时延估计领域里比较典型的算法。但是算法的抗噪性能随着信噪比的逐渐降低而大幅度减弱，对时延值进行估计时准确率下降而误差变大。而在使用二次相关算法对时延值进行估计时，增加了最开始就对一路声音信号施行自相关运算的步骤，以便增强算法的抗噪性能。为了增强二次相关算法在对时延值进行估计过程中的精度，因此将其与加权函数相结合得到二次相关GCC-PHAT-β算法，达到降低时延估计误差和提高算法抗干扰能力的目的。

二次相关GCC-PHAT-β算法[12]起初先对时域信号x1(t)进行自相关运算，同时对时域信号x1(t)、x2(t)进行第一次互相关运算，对分步获得的两个函数进行第二次的互相关运算，二次相关函数RRR(τ)由此取得，然后将其与加权函数ψPHAT-β相乘得到功率谱函数GR11R12(w)，检测经傅里叶逆变换后的功率谱函数所获得的函数峰值最大处，计算时延值。其原理框图如图3所示。

图3 广义二次相关算法原理框图Fig.3 Principle block diagram of generalized quadratic correlation algorithm

1.3.3 指数形式的二次相关GCC-PHAT-β时延估计算法

为了解决二次相关运算在信噪比降低时使得噪声强度增加，使其对时延估计的误差变大这种问题[13]，提出在二次相关算法的基础上,再乘以加权函数ψPHAT-β,对其得到的功率谱函数进行傅里叶逆变换，对其做指数运算并检测指数运算后函数的最大峰值处,从而计算出时延值。改进算法的原理框图如图4所示。

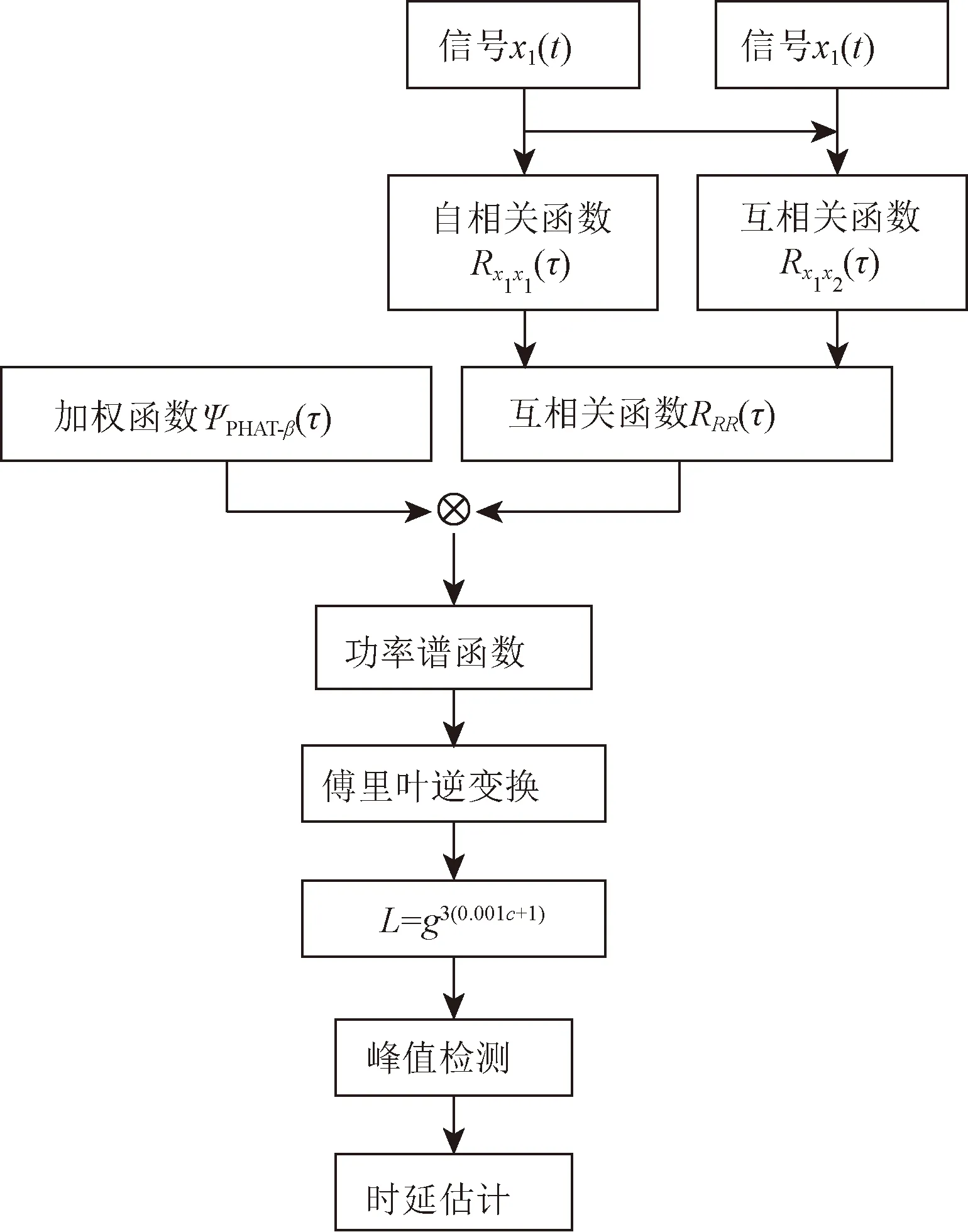
L为傅里叶逆变换指数运算结果；g为傅里叶逆变换后的相关函数图4 改进算法原理框图Fig.4 The schematic diagram of the improved algorithm

2 仿真研究

为了对改进算法的时延估计性能进行验证，利用软件MATLAB[14]构造了两路单频正弦波信号，信号频率为1 000 Hz、幅值为5。两路信号之间延时1.6 ms,并在其中分别加入高斯白噪声，采样频率50 kHz，采样点数1 024。在信噪比分别为-10、-5、0、5、10 dB的环境下，将GCC-PHAT-β算法、二次相关GCC-PHAT-β算法[12]以及指数运算形式的二次相关GCC-PHAT-β算法进行实验仿真，仿真结果如图5所示。

由图5(a)、图5(b)、图5(c)可得出，信噪比包含5 dB及以上时，GCC-PHAT-β算法、二次相关GCC-PHAT-β算法和本文改进算法均能够使函数的相关峰值锐化，但其锐化程度不同，相较于其他两种算法，虽然都能将峰值较为准确地估计出来，但本文改进算法中两路信号相关函数的最大峰值非常尖锐，信号峰值远高于旁瓣，该改进算法在信噪比0 dB以上时延估计性能远优于其他算法。

对比图5(d)、图5(e)可得，当信噪比小于0 dB时，GCC-PHAT-β算法获得的最大峰值几乎与噪声等高，系统难以准确判断时延值是最大峰值对应的时间值所得还是噪声所得，时延估计误差显著增大，二次相关GCC-PHAT-β算法亦获取不到较为凸出的峰值最大处，然而在本文改进算法中却相当凸出，远高于旁瓣。因此信噪比较低时，使用改进算法进行时延估计时可得到更为精准的时延值，对噪声有较强的抗干扰能力。

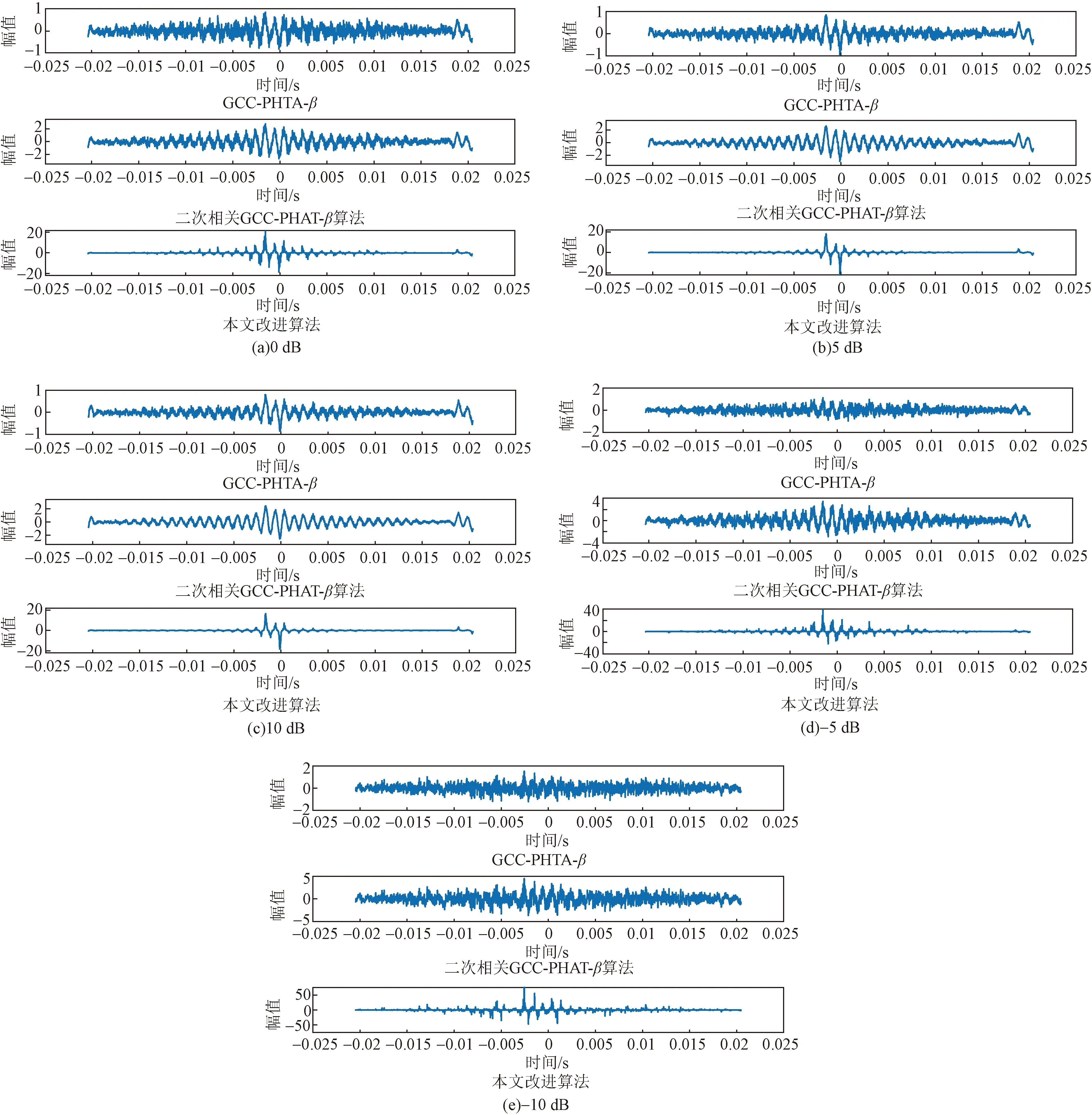
图5 不同信噪比下的仿真结果图Fig.5 Simulation results under different SNR

利用软件MATLAB对GCC-PHAT-β算法、二次相关GCC-PHAT-β算法和指数形式的二次相关GCC-PHAT-β算法在对时延值进行估计时产生的误差进行实验，进一步检验其对时延进行估计时的性能。实验所需信号源选用男声音频，频带范围为50～1 000 Hz，截取其中4 096个数据点，两路信号的时间延迟10个数据点，比较3种算法在进行时延估计时所产生的误差大小，确定-10～10 dB范围内的最优算法。

由图6可知，3种算法对时延值进行估计时所产生的误差随着逐渐降低的信噪比而渐渐增大。在0～10 dB时，3种算法进行时间延迟估计的误差无甚差别，都将接近于0;在-10～0 dB时, GCC-PHAT-β算法、二次相关GCC-PHAT-β算法的时延估计误差会随着信噪比的降低而变大,而改进算法的时延估计误差变化较为平缓,误差值在0～0.1范围内波动，时延估计性能在信噪比较低时依旧良好。以上结果表明,在对时延值进行估计时，指数形式的二次相关GCC-PHAT-β算法的性能在信噪比较低时优于其他两种算法。

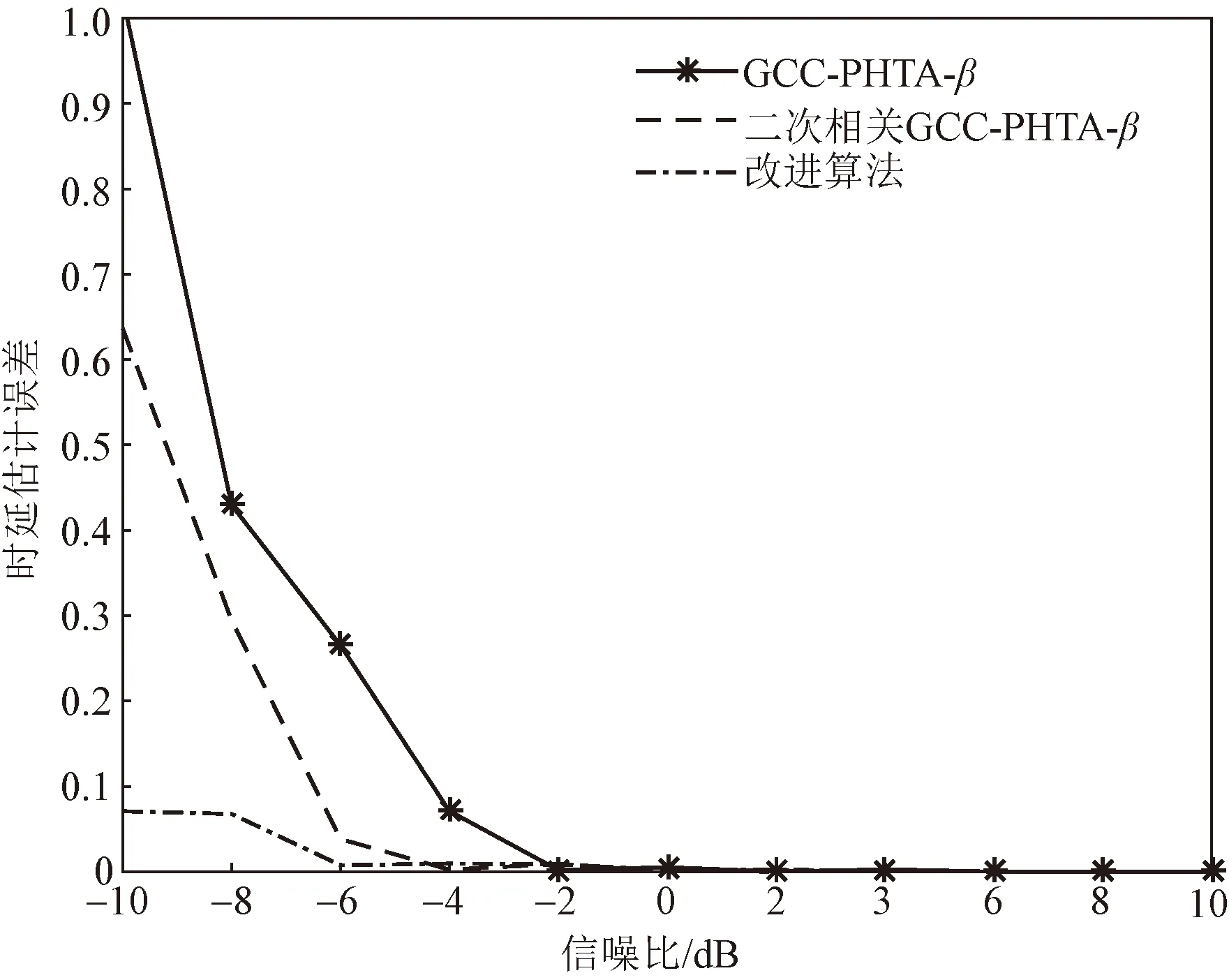
图6 三种算法的时延估计误差Fig.6 Delay estimation errors of three algorithms

3 结论

针对在低信噪比的情况下，GCC-PHAT-β算法和二次相关GCC-PHAT-β算法性能较差和时延估计误差变大的问题，讨论了一种对二次相关GCC-PHAT-β算法中功率谱函数进行傅里叶逆变换后再进行指数运算的改进算法,得出如下结论。

(1)进行指数运算的改进二次相关GCC-PHAT-β算法所获得的最大峰值更为尖锐凸出，使降低时间延迟误差的目标得以实现。

(2)在-10～10 dB的信噪比范围内，指数形式的二次相关GCC-PHAT-β算法的时延误差显著低于另外两种算法;在低于-10 dB内,改进算法仍具备一定优势。

总而言之，相对于GCC-PHAT-β算法和二次相关GCC-PHAT-β算法，改进算法在信噪比较低时的抗噪性能明显增强，时延估计误差显著下降。