基于健康监测的重载铁路连续刚构桥活载挠度可靠度评估

谈遂， 王翔

(1. 高速铁路建造技术国家工程研究中心， 长沙 410075； 2. 中南大学土木工程学院， 长沙 410075；3. 桥梁结构健康与安全国家重点实验室， 武汉 430034； 4. 中铁大桥科学研究院有限公司， 武汉 430034)

主梁挠度是反映桥梁结构刚度的重要指标，是反映桥梁结构服役性能的关键参数之一[1]。近年来，随着健康监测技术的发展，大量桥梁安装有挠度监测系统，也涌现出了一些先进的主梁挠度监测方法，例如连通管[2]、机器视觉[3]、毫米波雷达[4]、全球导航卫星系统(global navigation satellite system，GNSS)[5]等。运营期桥梁主梁挠度的获取越来越便利，监测数据精度也得到了大幅提升。如何有效利用主梁挠度长期监测数据进行桥梁服役性能评估，是桥梁健康监测领域迫切需要解决的问题之一[6]。

基于可靠度的评估方法可综合考虑桥梁运营过程中的多种状况，是在役桥梁服役性能评估的重要研究方向。目前，已有相关学者基于健康监测数据对桥梁服役状态进行了可靠度评估。Li等[7]采用滤波泊松过程描述车辆荷载引起的吊索随机索力响应，将一阶可靠性方法用于在设计基准期内桥梁在极端交通荷载分布下的安全性评估。高欣等[8]针对车辆荷载效应具有多峰分布的特点，提出了桥梁服役期内车辆荷载效应极值近似服从广义极值分布。阳霞等[9]采用极值统计理论对桥梁剩余服役期内的主梁应变极值进行了估计，并计算了不同承载能力下主梁的可靠度指标。鲁乃唯等[10]采用Rice公式对车辆荷载作用下主梁弯矩极值进行了外推。刘小玲等[11]基于南京长江三桥长期监测数据，提出了一种基于统计理论的主梁挠度安全评估与预警方法。周建庭等[12]进行了全桥实时有限元分析，提出了一种基于结构有限点实测位移响应的安全评估方法。樊学平等[13]针对控制监测点变形失效非线性相关的特点，采用主梁动态极值挠度，进行了大跨度桥梁主梁体系动态可靠性预测。Guo等[14]引入不确定方法对某混凝土梁长期挠度可靠度进行了量化评估。众多研究成果表明，基于活载效应的长期监测数据可有效实现运营期桥梁服役性能的可靠度评估，然而目前研究多集中在结构承载能力的可靠度评估，对于正常使用极限状态下的桥梁服役性能评估研究较少，且已有研究大多是利用应变、索力长期监测数据进行评估，对于精度更高、受环境干扰更小的主梁挠度监测数据利用较少。同时，以往研究实例以公路桥为主，对于载重高、服役环境恶劣的重载铁路桥梁应用较少。

现将活载挠度超限作为主梁竖向刚度不足的失效模型，采用串联模型描述各截面活载挠度失效模式之间的关系，并基于健康监测系统实测挠度数据对运营期重载铁路连续刚构桥活载挠度可靠度进行评估，为运营期重载铁路桥梁服役性能评估提供一种有效方法。

1 活载挠度极值概率模型建立

活载挠度极值X1,X2,…,Xn可看作独立同分布的随机变量，u为活载挠度阈值，当Xi>u时，Xi即为超越样本，该超越样本的概率分布函数Fu(x)可表示为

Fu(x)=P(X≤x|X>u)

(1)

当阈值u足够大时，超越样本Xi可被广义帕累托分布(generalized Pareto distribution，GPD)近似表达，则超越样本Xi的概率分布函数Fu(x,u,σ,ε)可表示为

Fu(x,u,σ,ε)=1-[1+ε(x-u)/σ]-1/ε

(2)

式(2)中：x≥u；1+ε(x-u)/σ>0；u为阈值；σ为尺度参数；ε为形状参数。

当活载挠度超越样本的概率模型为GPD时，其活载挠度极值的概率分布函数为广义极值分布(generalized extreme value distribution，GEVD)[10-11]，表达式为

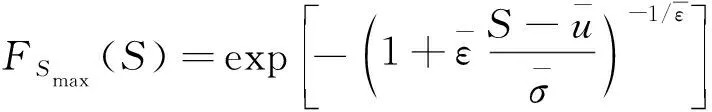
(3)

λn为服役期内超越样本发生的概率，计算公式为

λn=λ[1-Fu(x,u,σ,ε)]

(4)

式(4)中：λ为荷载效应发生概率。

2 基于串联模型的可靠性指标

活载挠度是反映桥梁健康状况的重要参数。一般而言，桥梁主梁上往往布置有多个挠度监测截面，各截面活载挠度的极限状态方程gi表达式为

gi=Ri-Li=0

(5)

式(5)中：Ri为截面i的挠度限值；Li为截面i实测的活载挠度极值，i=1,2,…,m，m为挠度监测截面数。

各截面活载挠度的可靠度指标βi，计算公式为

βi=Φ-1(1-Pfi)

(6)

式(6)中：Φ-1为标准正态分布的逆概率分布函数，Pfi为截面i活载挠度超限概率。

Pfi计算公式为

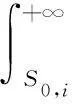
(7)

式(7)中：FSmax,i为截面i的活载挠度极值概率分布函数；S0,i为截面i的挠度限值。

采用串联模型描述各截面活载挠度失效模式之间的关系，即当m个挠度监测截面中，任一截面活载挠度超出限制，则代表体系失效。

根据式(6)，桥梁活载挠度可靠度指标的上界和下界计算公式为

βH=Φ-1(1-Pf,H)

(8)

βL=Φ-1(1-Pf,L)

(9)

式中：Pf,H和Pf,L分别为体系失效概率的上界和下界。

Pf,H和Pf,L分别可表示为

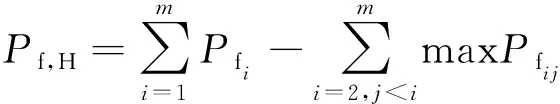
(10)

(11)

式中：Pfi为将各个截面失效概率按照从大到小排列，排序第i的截面失效概率，可定义为模式i失效概率，即模式1失效概率最高，模式m失效概率最低；Pfij为模式i和模式j的联合失效概率。截面失效概率为该截面挠度极值超出挠度限值的概率，可根据式(7)计算。

模式i和模式j的联合失效概率Pfij计算公式为

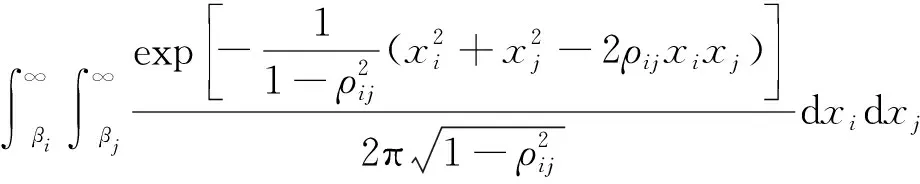
(12)

式(12)中：βi为模式i的可靠度指标；βj为模式j的可靠度指标；ρij为模式i可靠度指标与模式j可靠度指标的相关系数。

ρij计算公式为

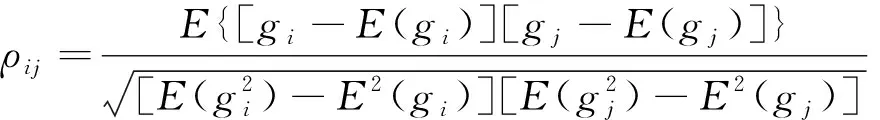
(13)

式(13)中：E为数学期望。

3 工程应用案例

3.1 工程概况

某重载铁路预应力混凝土连续刚构桥，跨径布置为96 m+132 m+96 m。为实时监测运营期主梁竖向挠度，该桥布置有基于连通管原理的主梁挠度监测系统，挠度测点布置S1、S2、S3、S4、S5如图1所示。

图1 主梁挠度测点布置图Fig.1 Measuring point positions of main girder deflection

3.2 活载挠度提取

2021年5月6号主跨跨中竖向挠度和环境温度典型监测结果如图2、图3所示。主梁挠度由趋势项和“突刺”组成，趋势项是由于环境温度变化引起，“突刺”则是由于列车过桥引起的活载挠度。

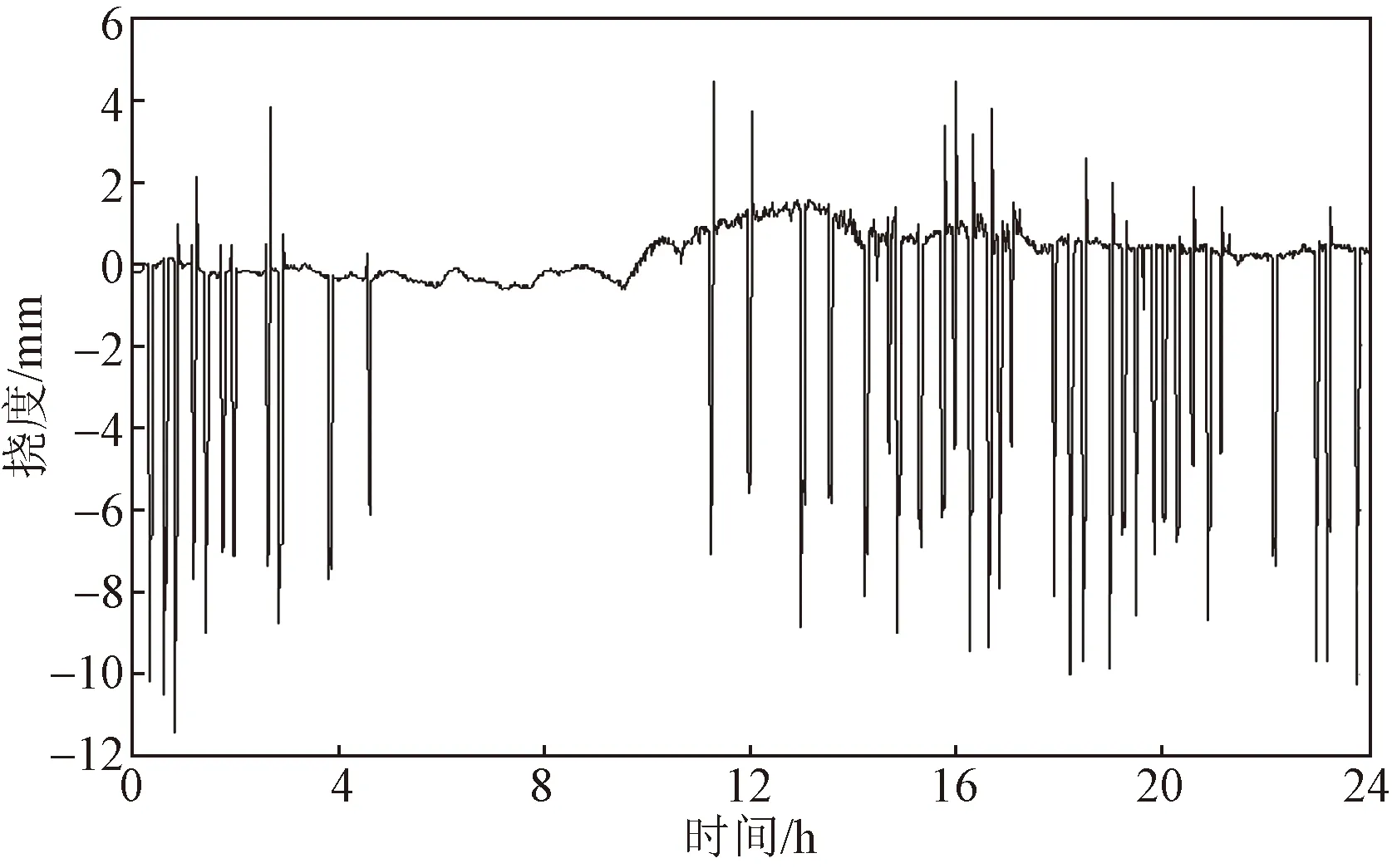
图2 主梁跨中竖向挠度日典型监测结果Fig.2 Monitoring results of vertical deflections at the middle of main span on a typical day

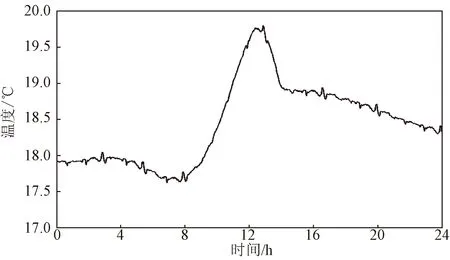
图3 环境温度日典型监测结果Fig.3 Monitoring results of ambient temperature on a typical day

采用小波变换[6]将主梁挠度中温度变化引起的趋势项去除，提取活载挠度。主梁温度挠度及与环境温度的相关性如图4、图5所示。图5中，K为拟合直线的斜率，R2为拟合直线的确定系数。K值反映了挠度对温度变化的敏感性，K值越大，挠度受温度变化的影响越大。主梁活载挠度日典型监测结果如图6所示。

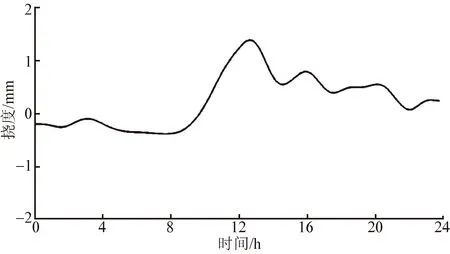
图4 主梁温度挠度日典型监测结果Fig.4 Monitoring results of temperature-induced deflections at the middle of main span on a typical day

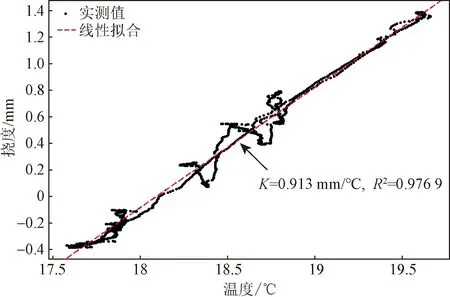
图5 主梁温度挠度与环境温度的相关性Fig.5 Correlation between temperature-induced deflections and ambient temperature

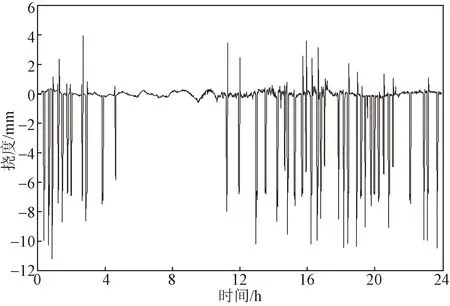
图6 主梁活载挠度日典型监测结果Fig.6 Monitoring results of vehicle-induced deflections at the middle of main span on a typical day

由图6可知，上午5：00—11：00时间段，桥面无列车通过，其余时时间段，列车荷载分布具有明显的随机性。重载列车通过时，主跨跨中挠度均在12 mm以内。

3.3 活载挠度极值分布模型

采用剩余寿命图法[15]确定活载挠度极值超样本概率分布函数Fu(x,u,σ,ε)中的阈值u，尺度参数σ，形状参数ε可通过最大似然法确定。

根据剩余寿命图法，当平均超出函数e(u)近似线性变化时，即为合理阈值。平均超出函数e(u)计算公式为

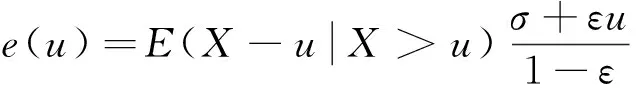
(14)

各截面活载挠度极值超样本概率分布模型Fu(x,u,σ,ε)中各参数如表1所示。

表1 活载挠度极值超样本概率分布模型参数Table 1 Parameters of probability model for extreme deflection of exceed threshold value

假定桥梁的服役年限T为100年，根据式(4)，计算服役期内超越样本发生的概率λn，将超越样本发生概率λn、阈值u、尺度参数σ、形状参数ε代入式(3)，即可建立活载挠度极值概率分布模型FSmax(S)。各截面活载挠度极值概率分布函数FSmax(S)中各参数如表2所示。

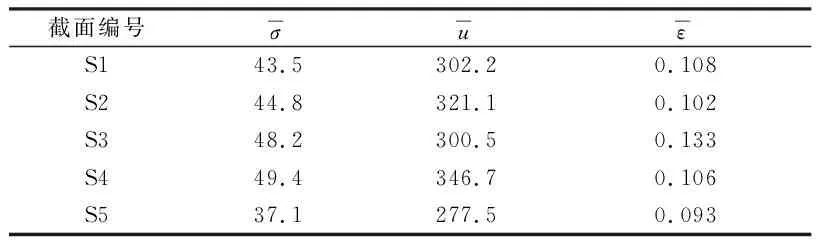
表2 活载挠度极值概率分布模型参数Table 2 Parameters of probability model for extreme deflection

3.4 各截面活载挠度可靠度评估结果

根据现行《铁路桥梁检定规范》(铁运函〔2004〕120号)要求，设置挠度限值分别L/1 800(L为跨度)，对活载挠度可靠性进行评估，以实现正常使用极限状态下的主梁竖向刚度评估。

根据活载挠度极值概率分布模型参数，建立各截面活载挠度极值概率分布，从而得到各截面活载挠度超限概率，将活载挠度超限概率代入式(6)，得到各截面活载挠度可靠度指标。

桥梁服役时间为100年时，各截面活载挠度可靠度指标如图7所示。

由图7可知，各截面活载挠度可靠度指标总体呈对称分布，但由于各截面活载挠度极值分布存在差异，主梁对称截面活载挠度可靠度指标也略有差异。由于主跨跨中截面挠度受重载列车影响较大，主梁跨中截面活载挠度可靠度指标最小，为4.32。

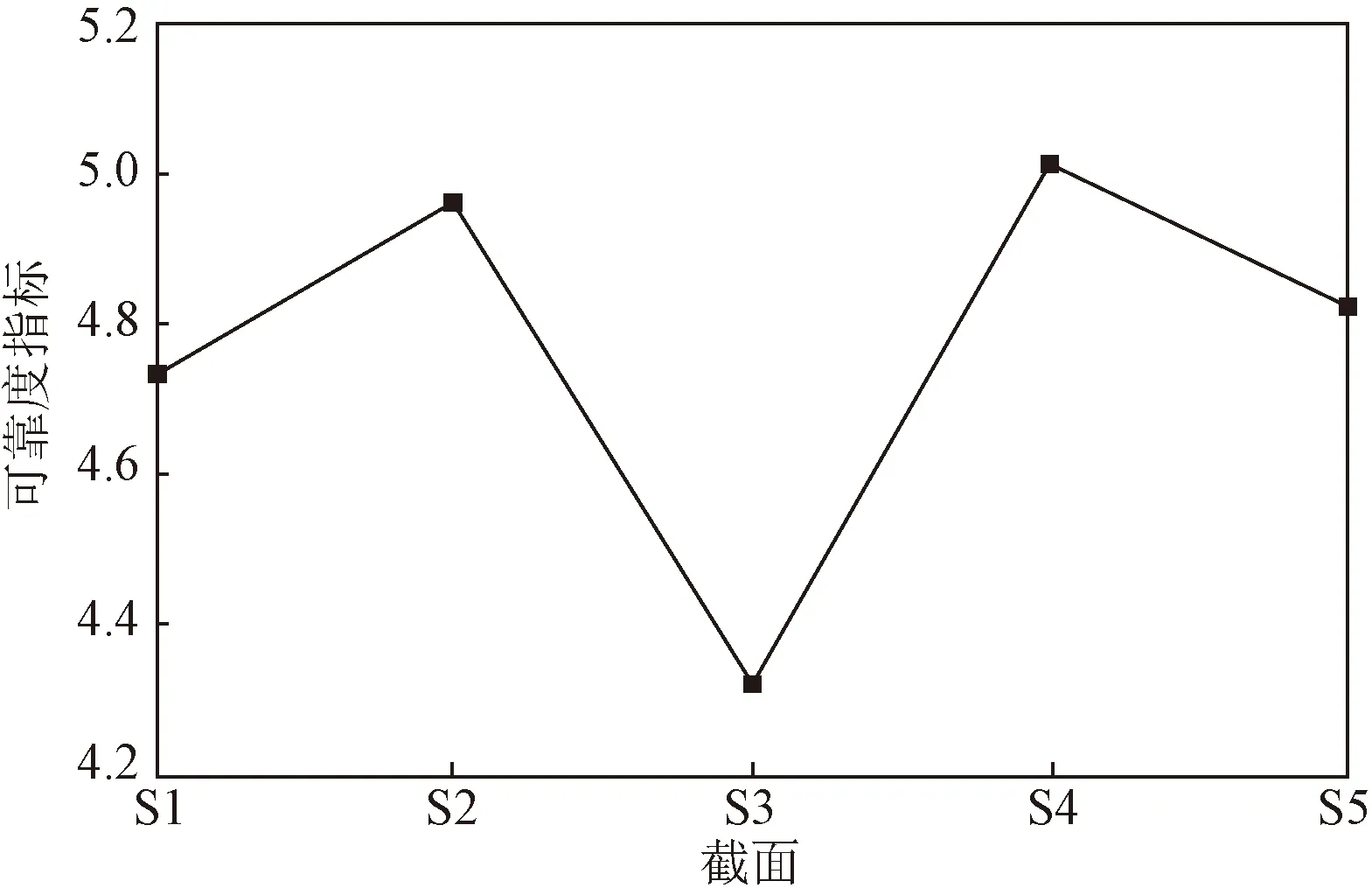
图7 主梁各截面活载挠度可靠度指标Fig.7 Vehicle-induced deflection reliability of girder sections

各截面活载挠度可靠度指标随服役时间的变化规律，如图8所示。

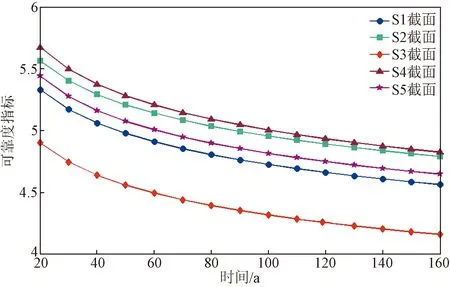
图8 活载挠度可靠度指标随服役时间的变化规律Fig.8 Change of reliability indices of vehicle-induced deflection vs service time

由图8可知，各截面活载挠度可靠度指标在服役初期下降较快，随着服役时间的增加，可靠度指标下降速率趋于稳定，即使桥梁服役时间达到160年，各截面活载挠度可靠度指标仍达到4.16以上。

3.5 桥梁体系活载可靠度评估结果

根据式(13)计算不同截面活载挠度可靠度指标间的相关系数ρij，如图9所示。

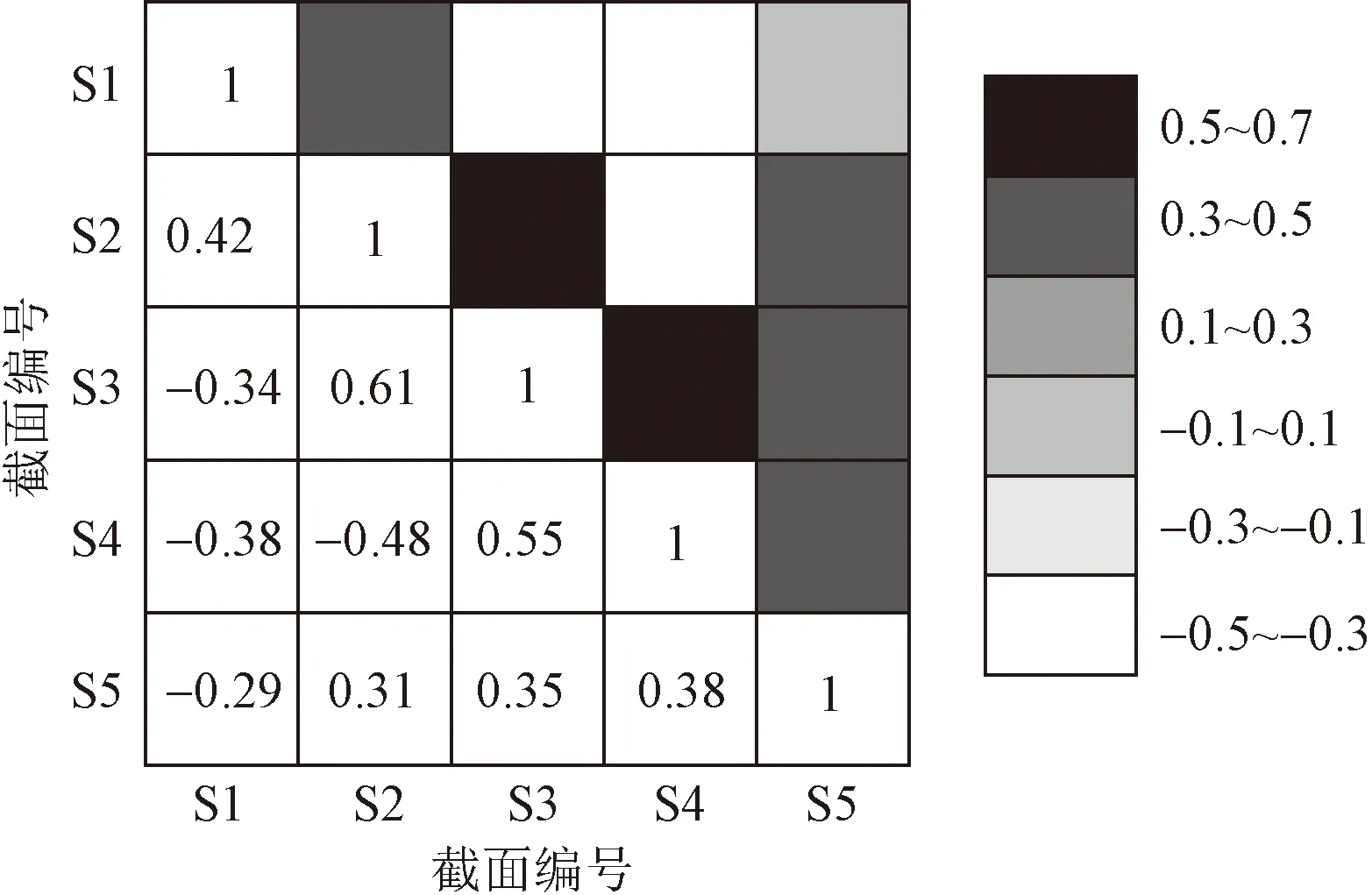
图9 各截面活载挠度可靠度指标间的相关系数Fig.9 Correlation coefficient of vehicle-induced deflection reliability with different sections

将ρij代入式(12)，根据式(8)～式(11)，计算得到桥梁活载挠度可靠指标的上界和下界。该桥于2020年5月采用体外索对主梁进了加固，加固前后桥梁体系活载挠度可靠指标上界及下界随服役时间的变化如图10所示。

由图10可知，桥梁体系活载挠度可靠度指标下界和上界接近，桥梁体系活载挠度可靠度指标随服役时间的变化与主跨跨中截面十分相似，表明主跨跨中是主梁活载挠度可靠性的控制截面。桥梁经过体外索加固后，主梁刚度增加，体系活载挠度可靠度指标上升。相比加固前，服役时间为100年时，可靠度指标上界和下界分别上升了5.21%、5.23%。

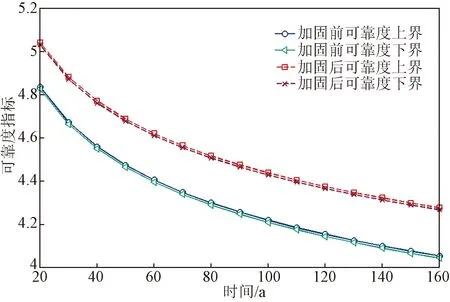
图10 桥梁体系可靠度指标随服役时间的变化规律Fig.10 Change of bridges system reliability with service time

目标可靠度指标为2.5[16]。桥梁经加固后，服役时间为160年时，桥梁体系活载挠度可靠度指标βH≈βL=4.3，大于目标可靠度指标。

4 结论

将主梁活载挠度超限作为竖向刚度不足的失效模型，采用串联模型描述各截面活载挠度失效模式之间的关系，并基于健康监测系统实测数据对重载铁路连续刚构桥运营期活载挠度可靠度进行评估，有以下结论。

(1)活载挠度超限可作为主梁竖向刚度不足的失效模型，串联模型综合了主梁各监测截面挠度数据，可有效反映各截面活载挠度失效模式之间的关系。

(2)主梁各截面活载挠度可靠度指标总体呈对称分布。由于主跨跨中截面挠度受重载列车影响较大，主跨跨中截面活载挠度可靠度指标最小，为主梁活载挠度可靠性的控制截面。活载挠度可靠度指标在服役初期下降较快，随着服役时间的增加，可靠度指标下降速率趋于稳定。

(3)桥梁经过体外索加固后，主梁刚度增加，活载挠度可靠度指标上升。相比加固前，服役时间为100年时，桥梁活载挠度可靠度指标上界和下界分别上升了5.21%、5.23%。桥梁服役时间为150年时，桥梁活载挠度可靠度指标近似为4.3，大于目标可靠度指标。