基于Treloar 实验数据的超弹性材料完全本构关系研究1)

韩磊 王新彤 李录贤

(西安交通大学航天航空学院,机械结构强度与振动国家重点实验室,飞行器环境与控制陕西省重点实验室,西安 710049)

引言

橡胶材料等弹性体因其卓越的减震性、柔韧性及密封性等,已广泛应用于轮胎、密封件或振动支座等各类橡胶制造行业[1-3].这些材料的超弹性力学行为,通常基于应变能密度函数(简称应变能函数)来研究.近几十年来,人们已经提出大量模型来预测材料的超弹性行为[4-9].例如文献[5],基于遗传算法利用多目标优化程序,提出了一种参数识别方法,比较研究了44 种超弹性本构模型对多种变形模式下实验曲线的拟合精度.彭向峰等[10]从不同体积变化形式、多变形模式和全范围变形程度3 方面对超弹性本构关系进行总结分析,并提出了超弹性材料完全本构关系的构造步骤及研究方法.随着计算能力和非线性数值模拟技术的快速发展,有限元分析已成功应用于大变形复杂橡胶构件的结构优化设计和可靠性分析[11-12],但是,若没有采用准确的超弹性本构模型,就无法获得高精度的应变和/或应力分布的数值结果.

目前,大多数本构模型可对实验数据进行高精度的预测,尤其是针对单轴拉伸实验数据.Destrade等[13]采用多种形式的应变能函数对单轴拉伸实验的全变形范围进行了参数识别,但该模型对等双轴拉伸实验曲线的预测效果较差.Han等[14]采用(I1-3)m和(I2-3)m型应变能函数分阶段逐步对单轴拉伸实验数据进行参数识别,得到了令人满意的预测曲线,并保持了材料的初始剪切模量,但对等双轴和纯剪实验数据的预测效果却不尽人意.魏志刚等[15]基于平面应力变形状态,构建了一类依赖于第一和第二主伸长比的本构模型形式,可使用单类实验数据识别得到可靠的模型参数,但其单轴拉伸变形范围仅有400%.Steinmann等[6]和Hossian等[16]发现仅用一种变形模式得到的模型参数并不能有效预测其它变形模式的实验结果,即使可很好描述单轴和纯剪切变形模式的八链模型[17],对等双轴载荷响应的预测也不能令人满意.

理论上,材料的本构模型并不因变形模式而不同,且最佳模型能够用最少数量的材料参数描述超弹性体的完整行为[18].鉴于此,Bien-Aimé等[19]提出了一种新的类橡胶材料模型,运用遗传算法,通过预测Treloar(3 种变形模式)和Nunes(简单剪切)的实验数据,建立了材料的本构模型.Blaise等[20]基于Hart-Smith 模型和Gornet 修正模型,提出一种不可压缩超弹性模型,很好预测了橡胶材料在多种变形模式下的应力-应变响应.考虑到超弹性材料在各种载荷下均表现出了S 形的应力曲线,指数型函数[21-23]也是应变能函数的一个很好选择.Darijani等[21]的工作表明,指数型应变能函数也可准确预测可压和不可压橡胶材料的实验数据.基于文献[21]的框架,Mansouri等[22]构造了一组新的应变能函数,对大变形条件下具有J 形和S 形力学行为的弹性体和软组织材料均具有良好的预测能力.然而,对一般超弹性材料,指数型应变能函数的适用性仍是一个需要解决的问题.

随着超弹性材料断裂问题的研究与应用,为了预测较大变形范围和复杂变形模式,幂函数型应变能函数的指数也会出现小于1 的情形,此时,以(I1-3)和(I2-3)为底的幂函数(例如文献[8,19-20,24-25]),虽可提高大变形阶段的预测精度,但在初始状态的小变形阶段,面临更大的应力奇异问题.鉴于此,Carroll[26]建议以I1和I2为底,提出了3 参数幂类应变能函数,依次通过单轴和等双轴拉伸实验数据对模型参数进行了识别,所得本构模型对纯剪变形模式也给出了令人满意的预测效果.该模型克服了初始状态时会出现应力偏差大的局限,但预先指定的幂指数,限制了模型的预测精度.一些学者也采用其它技术来提高本构模型的预测效果和稳定性.徐中明等[27]提出超静定方程方法来识别橡胶的材料参数,预测效果显示了该方法的有效性和可靠性.肖锐等[28]在熵弹性模型的基础上引入缠结约束效应,其本构模型能准确描述不同变形模式的应力响应,并揭示了缠结约束效应对超弹性材料宏观力学行为的影响.

本文基于Treloar 的单轴拉伸、等双轴拉伸和纯剪切3 种不同变形模式的实验数据,采用和两类非指定指数的幂函数型应变能函数,建立超弹性材料的完全本构模型.第1 节首先对3 种基本实验曲线的特点进行分析;接着,基于共有的应力条件,推导单轴、等双轴拉伸和纯剪切3 种基本变形模式的本构关系;最后,对3 种变形模式下和两类基本应变能函数的本构特性进行讨论.第2 节提出一种新的模型参数识别方法,以3 种实验数据与模型预测的总体误差泛函最小为目标,对模型参数进行识别,构建满足3 种基本变形模式、适合全程大变形范围的完全本构关系.第3 节将本文结果与已有文献结果进行比较.第4 节总结全文工作并给出结论.

1 基本理论

1.1 实验数据分析

Treloar 对含8%硫的硫化橡胶分别开展了单轴拉伸(简称ST)、等双轴拉伸(简称ET)和纯剪切(简称PS) 3 种变形模式的实验测试,所得实验数据如表1～ 表3 所列[6,14],其应力随伸长比的变化关系如图1 所示.

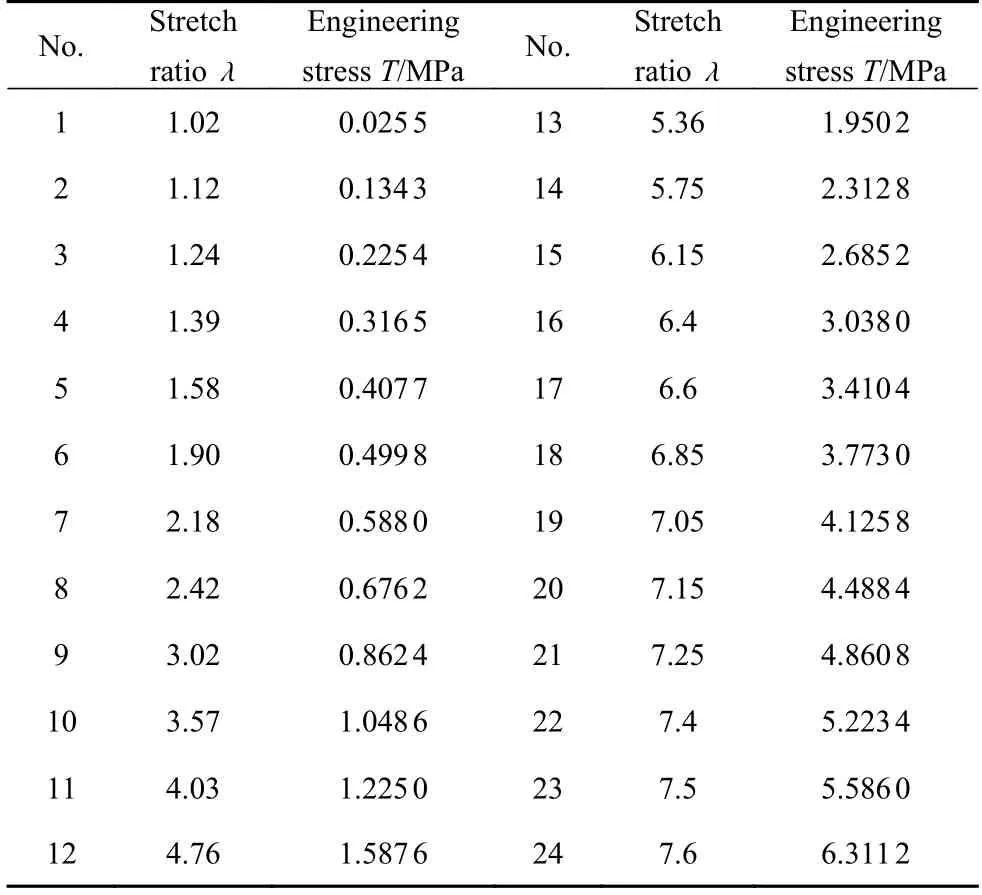
表1 单轴拉伸变形模式的实验数据Table 1 Experimental data of the ST deformation mode

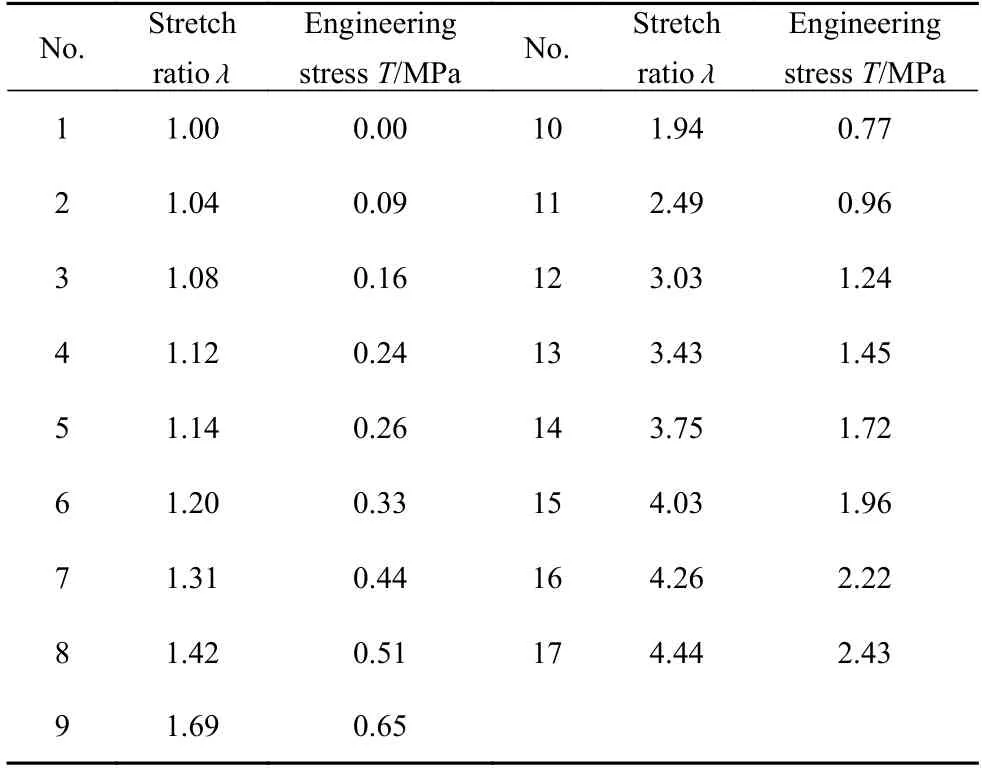
表2 等双轴拉伸变形模式的实验数据Table 2 Experimental data of the ET deformation mode

表3 纯剪切变形模式的实验数据Table 3 Experimental data of the PS deformation mode

从图1 可以看出,这3 组实验曲线均表现出高度的非线性.单轴拉伸和纯剪切曲线在伸长比为1～5 之间的变化规律基本一致,等双轴拉伸实验曲线则更为陡峭.

图1 ST,ET和PS 实验数据汇总Fig.1 Collection of experimental data under ST,ET and PS states

1.2 本构理论

超弹性材料的力学特性可以用它的应变能函数W予以描述.一般地,应变能函数可表示为变形梯度张量F的函数W(F),考虑到材料性能的客观性,应变能函数又可表示为右拉伸张量U的函数W(U).在大变形分析中,右Cauchy-Green 张量C=U2=FTF是描述物体变形(例如Green 应变)的一个重要物理量,为此,与大多数文献(例如文献[1,5,23])所采用的等价方式一样,本文假定应变能函数W为右Cauchy-Green 张量C的3 个不变量I1,I2和I3的函数W(I1,I2,I3),3 个不变量的含义为

其中,λ1,λ2和λ3为拉伸张量U(或变形梯度张量F)的3 个特征值,在物理上解释为物体的3 个主伸长比.

材料的体积变形比J=λ1λ2λ3=.对于不可压材料,有J=1,此时,用第一Piola-Kirchhoff应力张量P表示的本构关系为

其中,p是与不可压约束相关的静水压力.对于主方向的应力ti(i=1,2,3),式(2)又可表示为

对于单轴拉伸、等双轴拉伸以及纯剪切3 种基本变形模式,都具有t3=0的相同应力条件,因而,其本构特性在主应力空间均可表征为加载方向的应力T与该方向上主伸长比 λ 间的关系式,下面推导这3 种基本模式的具体本构关系.

(1) 单轴拉伸模式的本构关系

对于单轴拉伸模式,除了t3=0的应力条件外,还具有 λ1=λ和λ2=λ3=λ-1/2的变形特征,将其代入式(6),得出单轴拉伸时的本构关系为

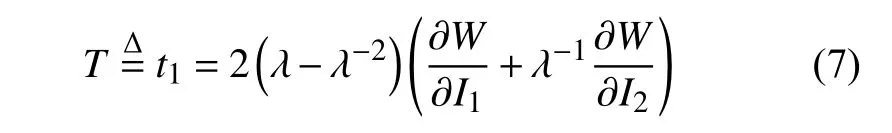
(2) 等双轴拉伸模式的本构关系

对于等双轴拉伸模式,除了t3=0的应力条件外,还具有 λ1=λ2=λ和λ3=λ-2的变形特征,将其代入式(6),得出等双轴拉伸时的本构关系为

(3) 纯剪模式的本构关系

与简单剪切变形时应变主轴在加载过程中不断旋转变化不同,纯剪变形的应变主轴在加载过程中保持空间方向不变.这样,纯剪变形可通过如图2 所示的宽高比b/h0足够大的薄橡胶板拉伸试验来实现.

图2 纯剪试件示意图Fig.2 Schematic of pure shear specimen

于是,对于纯剪变形模式,除了t3=0的应力条件外,将具有 λ1=λ,λ2=1 以及 λ3=λ-1这样一个极为特殊的双轴拉伸变形特征[29],将其代入式(6),得出纯剪时的本构关系为

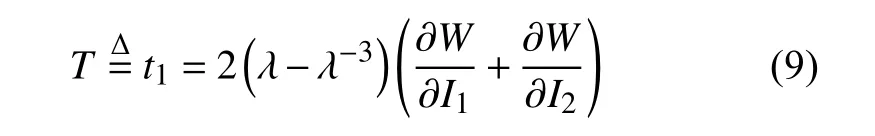
1.3 基本应变能函数的本构特性

在1.2 节中,简单拉伸、等双轴拉伸以及纯剪3 种变形模式的本构关系都表示成了T与主伸长比λ之间的关系.下面研究应变能函数分别为W1=I1m和W2=I2m两种基本幂函数形式时材料的不同本构特性.根据式(1),I1和I2恒大于等于3,所以,以两者为底时指数m可允许取小于1 的正实数.

对于应变能函数为W1=I1m的情形,根据式(7)～式(9),得到其应力T1的表达式为

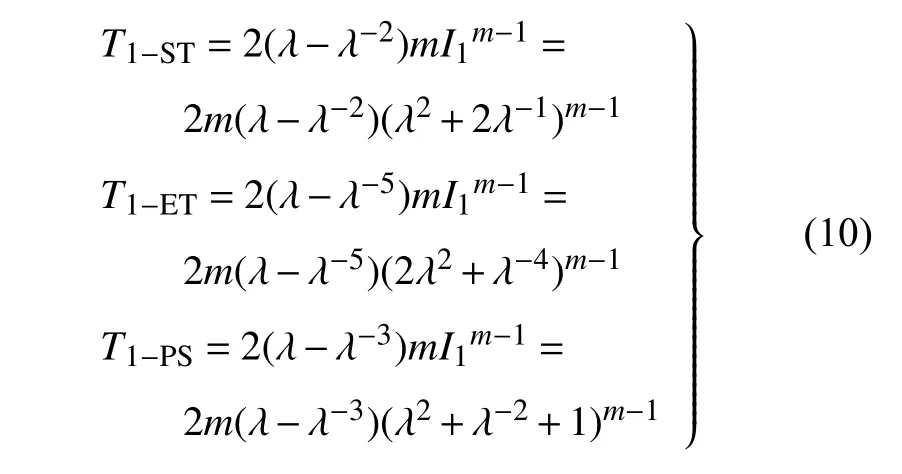
对于应变能函数为W2=I2m的情形,根据式(7)～式(9),得到其应力T2的表达式为

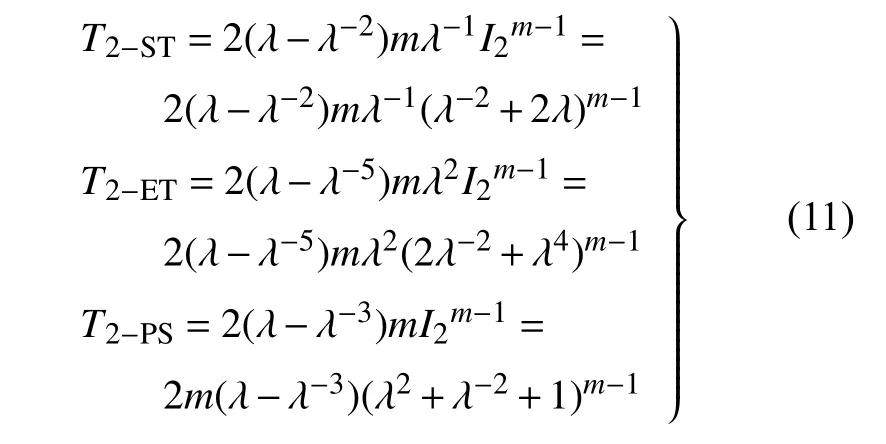
典型m取值时式(10)和式(11)所表示的不同变形模式的本构规律分别如图3和图4 所示.

由图3 可以看出,对于W1=I1m型基本应变能函数,3 种变形模式的规律基本一致.当m<1 时,应力在伸长比较小时变化非常陡峭,随着伸长比的增大,应力变化逐渐趋于平缓;当m>1 时,应力随伸长比的变化与m<1 时呈相反趋势,即先平后陡的增长变化;3 种变形模式应力大小的次序不随m发生变化,均依次为等双轴最大、纯剪次之、单轴最小.

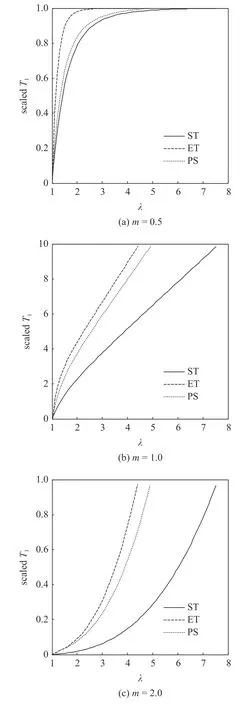
图3 典型m 取值时 W1=I1m对3 种变形模式的本构描述Fig.3 Constitutive behavior of three deformation modes described by W1=I1mfor typical values of m

对于图4 表示的W2=I2m型基本应变能函数,情形则有所不同,3 种变形模式下以及不同m取值时,应力的变化都表现出复杂的非线性行为.

图4 典型m 取值时 W2=I2m所表征的三种变形模式本构特性Fig.4 Constitutive behavior of three deformation modes described by W2=I2mfor typical values of m

2 完全本构关系的建立

超弹性材料的非线性及其多样性,决定了材料本构模型的形式及其参数取值需要多种变形模式及全变形范围的实验去验证.例如,仅运用单轴拉伸实验数据确定的本构关系及其参数,一般并不能很好预测等双轴和纯剪两种变形模式时的应力变化特性(参考文献[22]及3.2 节的讨论).为了同时兼顾不同模式下的实验数据,采用3 种变形模式实验数据对本构参数进行同步识别的思想,以实现本构模型对不同变形模式同时达到最佳预测精度的目标.

2.1 初始阶段本构关系的建立

如图1 所示,超弹性材料较小变形的初始阶段,除了具有因不同物理机制决定的复杂变化关系外,它还是获取超弹性材料基本材料参数(例如初始剪切模量[14])的重要依据.因而,对该区域的划分及预测精度就显得尤为重要.

理论上,初始阶段选取的变形范围越小越好,但考虑到该阶段是实验的初始阶段,数据分散性较大[6],经分析3 种模式的实验数据,我们确定取伸长比不超过1.12 的6 组实验数据为初始阶段,具体如表4所示.利用最小二乘法,通过寻求该阶段所有实验点处预测的总体误差泛函最小,以获取最佳模型参数.

表4 初始阶段数据及其对应变形模式Table 4 Data in the initial regime and the associated deformation modes

众所周知,在非常小变形情形下,超弹性材料都服从neo-Hookean 模型[30],即WI=A1I1,也就是说,式(10)中的m=1.

根据式(10),并结合表4 的数据,得到6 组数据的误差分别为

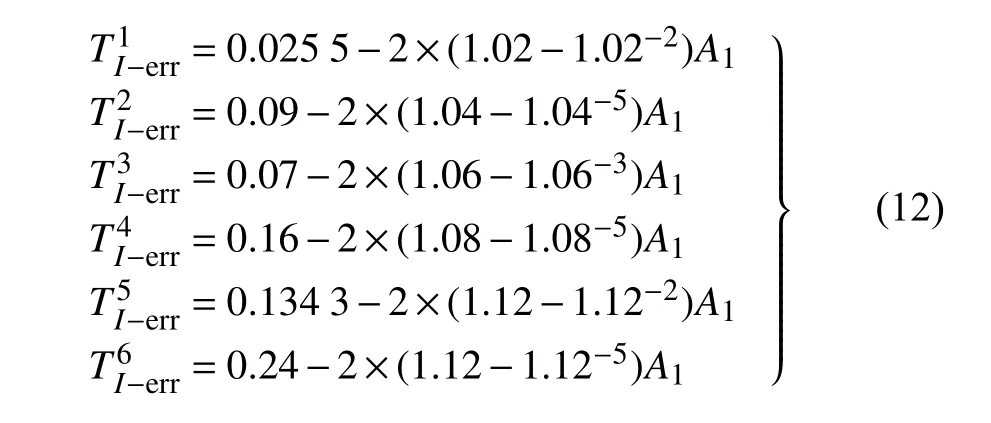
定义该阶段的总体误差泛函为

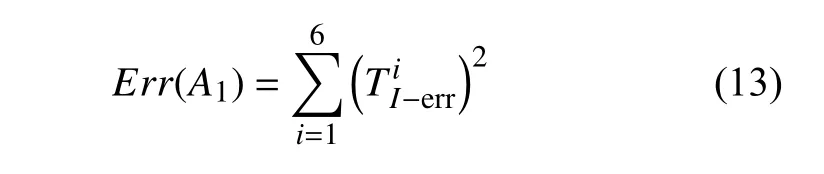
通过对总体误差泛函Err(A1) 关于本构参数A1求变分,解析得到A1=0.206 7,进而获得材料的初始剪切模量[14]G=2A1=0.413 4 MPa.

2.2 全变形范围本构关系的建立

借鉴Carroll[26]将单轴拉伸全变形范围分为两个阶段的做法,本文将3 种变形模式实验曲线除初始阶段的剩余部分作为第2 阶段进行统一处理.考虑到2.1 节已得到材料在初始阶段的本构特性,通过TU-E=TE-TI,将得到图5 所示的3 种模式全变形范围的更新实验数据TU-E.

图5 3 种变形模式的更新实验数据Fig.5 Updated experimental data of three deformation modes

经分析图3和图4 基本应变能函数所表征的本构特性,图5 的高度非线性变化很难采用单一基本应变能函数予以表征,为此,本文假设应变能函数为

其中两个不同指数项I1的引入是为了后续与文献[26]结果进行比较.

根据式(7)～式(9),针对式(14)的应变能函数,得到不同模式的本构关系为

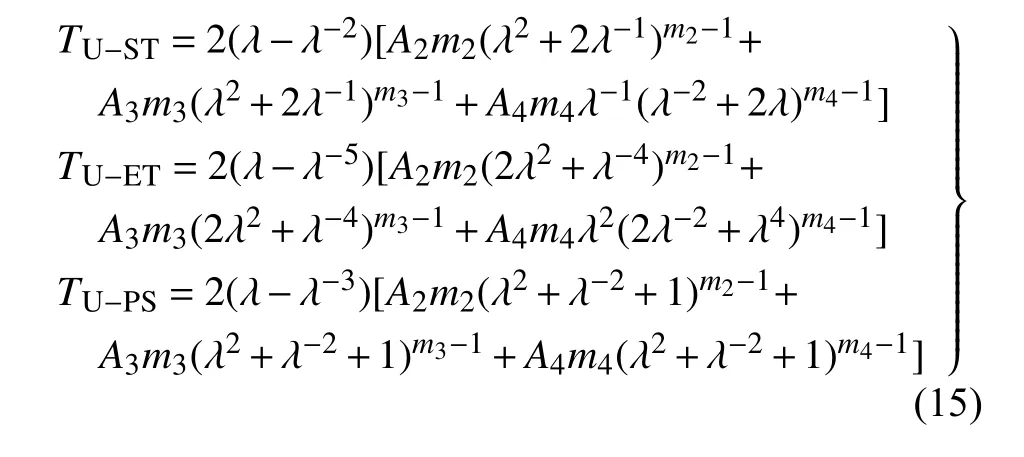
结合图5 的更新数据,先计算各模式的偏差,再仿式(13)构造3 种模式的总体误差泛函,最后运用1stOpt 软件,在Err=0.163 2 时识别得到模型参数为

采用式(15)的本构关系和式(16)的模型参数,对更新数据的预测效果如图6 所示.

图6 对3 种变形模式更新实验数据的预测效果Fig.6 Predicted effect for the updated experimental data of three deformation modes

2.3 完全本构关系的建立

根据2.1 节和2.2 节的分析,我们得到该材料的总体应变能函数为

由于式(17)应变能函数的选取及其参数识别同时考虑了3 种不同变形模式以及全变形范围,我们将式(17)代入式(2)后得到的本构关系,称之为该材料的完全本构关系,其退化形式可以是主应力形式的式(3),或单轴拉伸变形模式的式(7)、等双轴拉伸变形模式的式(8)和纯剪切变形模式的式(9).

完全本构关系对实验曲线的预测效果如图7 所示,单轴拉伸时的最小二乘误差LSE为2.51%、等双轴拉伸时LSE为2.76%、纯剪切时LSE为2.45%,对3 种模式实验均具有满意的整体预测精度.

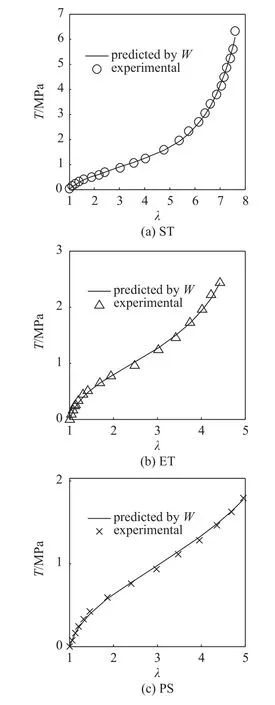
图7 完全本构关系对3 种不同模式实验曲线的预测效果Fig.7 Predicted effect of complete constitutive relation for the three different modes

依据式(17)及文献[14],得到该材料初始剪切模量为

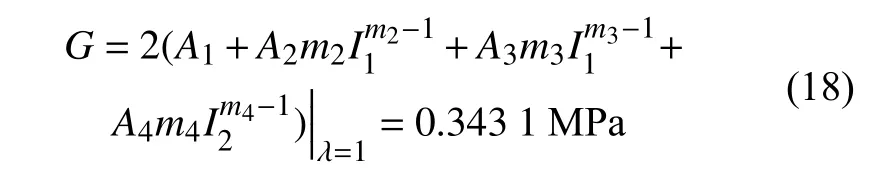
可以看出,初始模量不再保持为初始阶段确定的 2C1=0.413 4 MPa,降低了约17%,可认为是同时兼顾3 种变形模式实验数据后对材料初始剪切模量的有效修正.

3 比较与讨论

3.1 与文献[26]结果的比较与讨论

Carroll[26]将两种不同模式的实验曲线分成两段,通过分析各段的变化特征,采用指定指数的幂函数形式,将应变能函数表示为

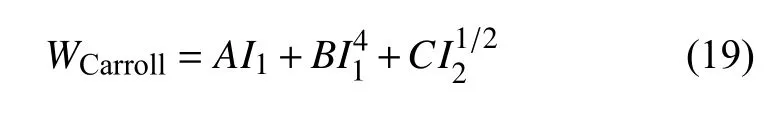
运用实验数据,Carroll[26]识别得到的模型参数为

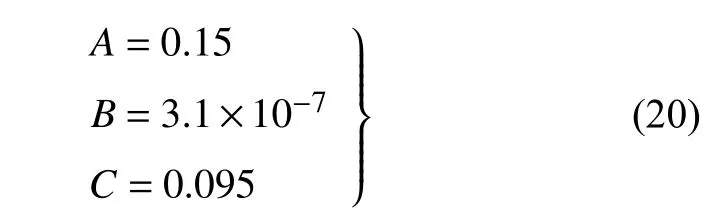
式(19)和式(20)对3 种变形模式实验曲线的预测精度如表5 所示.可以看出,对于3 种变形模式实验数据,本文得到的式(17)的预测精度均优于式(19).

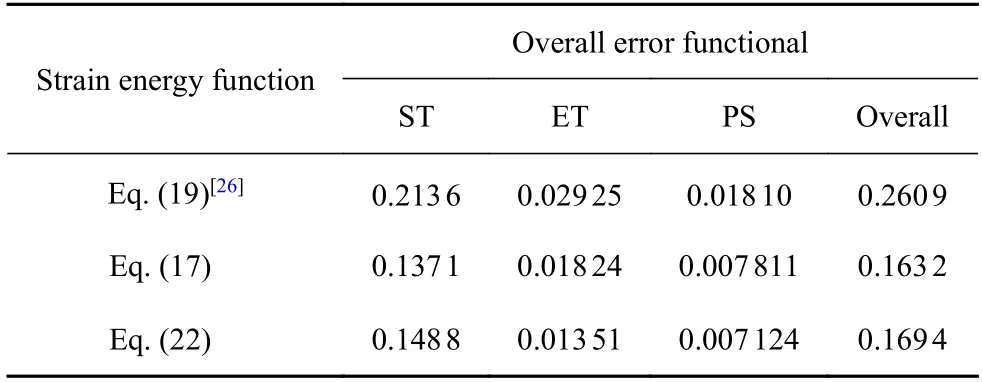
表5 不同本构模型的预测精度比较Table 5 Comparison of prediction accuracy of different constitutive models

分析式(16)中的指数取值发现,Carroll 模型[26]碰巧是一种与本文非整数指数接近的可选整数指数(例如m2=1和m3=4) 或半整数指数(例如m4=0.5)模型.实际上,如若假定本文模型中m2=1为给定指数,可进而识别得到

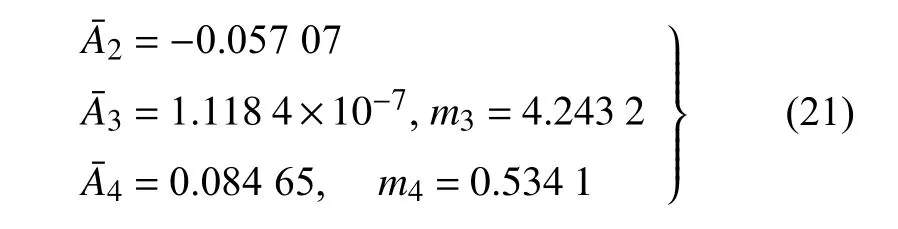
最终得到一种可选模型为

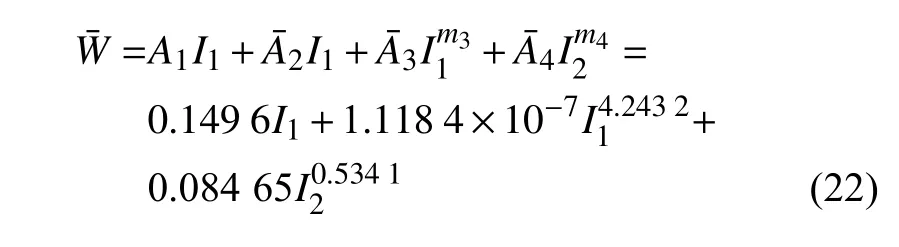
值得注意的是,此时累加得到的I1项系数0.149 6与Carroll 模型[26]中的系数0.15(参考式(20))非常吻合.式(22)模型的预测精度也列于表5,可以看出,由于仍具有两个非指定的指数m3和m4,模型预测的总体误差泛函虽稍逊于式(17),但仍明显优于Carroll 模型的式(19).

3.2 与Destrade 工作的比较与讨论

针对单轴拉伸全变形区域,Destrade等[13]提出了多个超弹性材料模型.单纯从对单轴拉伸实验预测的效果看,Destrade 模型的误差泛函在0.06907～0.107 2 之间,优于本文模型对单轴拉伸模式的最佳误差泛函0.137 1.但当Destrade 模型用于等双轴拉伸或纯剪变形两种与单轴拉伸区别较大的模式时,其预测精度却差强人意.以文献[13]中最好的W1-GT和W2-GT两种模型为例,参考图8,二者对纯剪模式的误差泛函分别为0.0104和0.026 4,与本文模型和Carroll 模型(参考表5)基本相当;但对等双轴拉伸模式的误差泛函已达0.435 8和0.438 8,偏差太大;然而,本文模型对等双轴模式仍能表现出强健的预测能力.

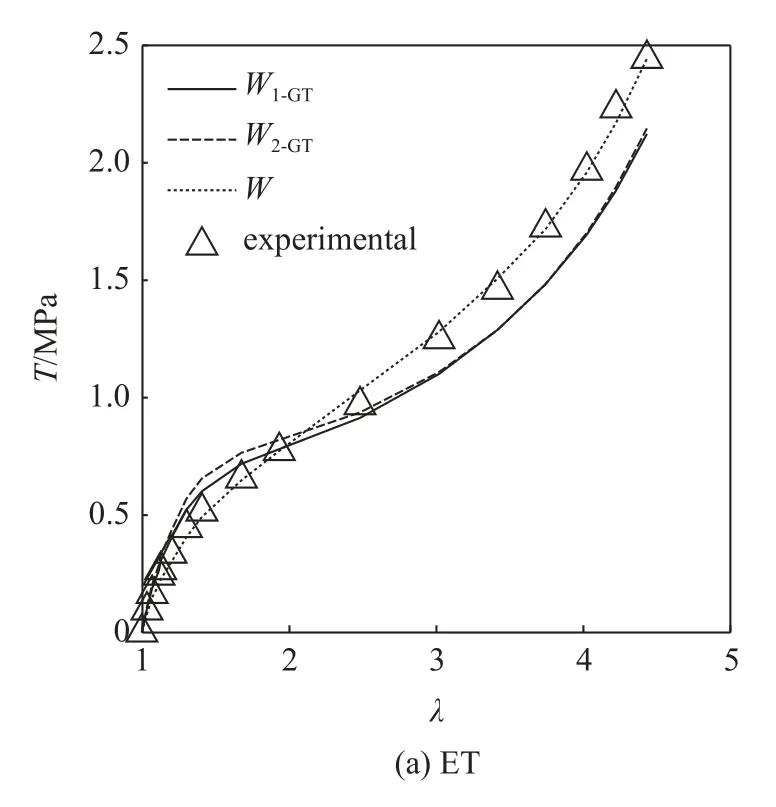
图8 典型Destrade 模型对不同变形模式实验数据的预测效果Fig.8 Predicted effect of typical Destrade models for experimental data of different deformation modes

3.3 与文献[22]工作的比较与讨论

Mansouri等[22]根据第1和第2 应变不变量构造了指数型应变能密度函数,对多种类橡胶材料以及生物软组织材料进行预测,其本构关系具有普遍性.考虑到本文工作均基于Treloar 的实验数据,文献[22]中针对该数据得到的本构模型为

由于文献[22]中的单轴实验数据与本文不一致*实际上,与其他多个文献(如文献[6,13])也不一致,此处只比较等双轴拉伸和纯剪两种变形模式,其结果如图9 所示.经计算,式(23)对等双轴拉伸和纯剪变形预测的误差泛函分别为0.4607和0.082 62,最小二乘误差分别为LSE=15.78%和LSE=8.22%,均明显大于本文模型的预测误差(参考表5).

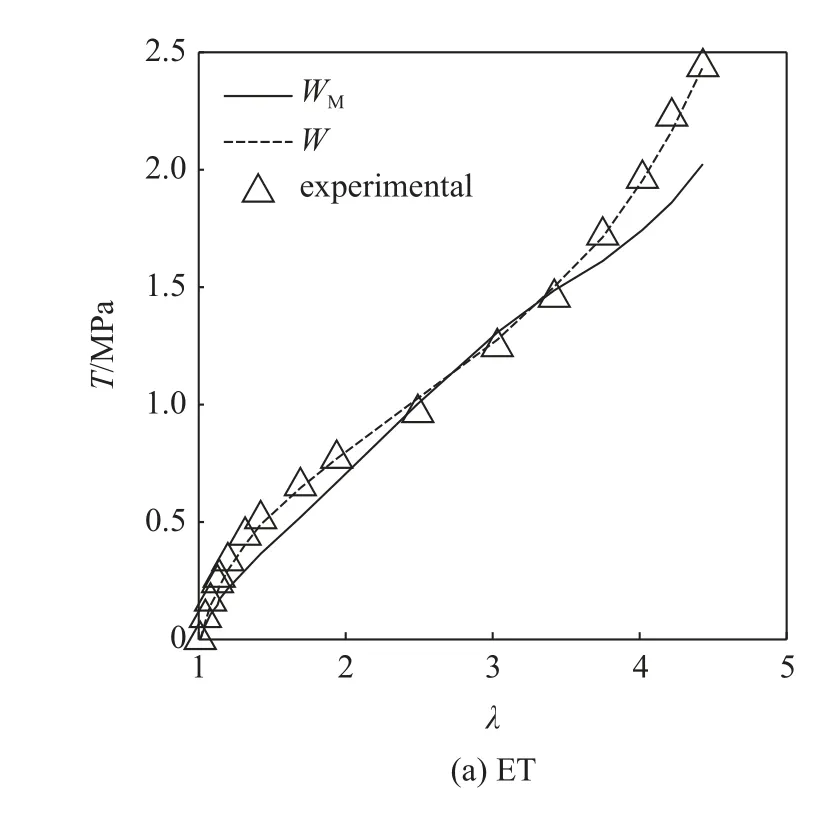
图9 Mansouri 模型对不同变形模式实验数据的预测效果Fig.9 Predicted effect of the Mansouri model for experimental data of different deformation modes

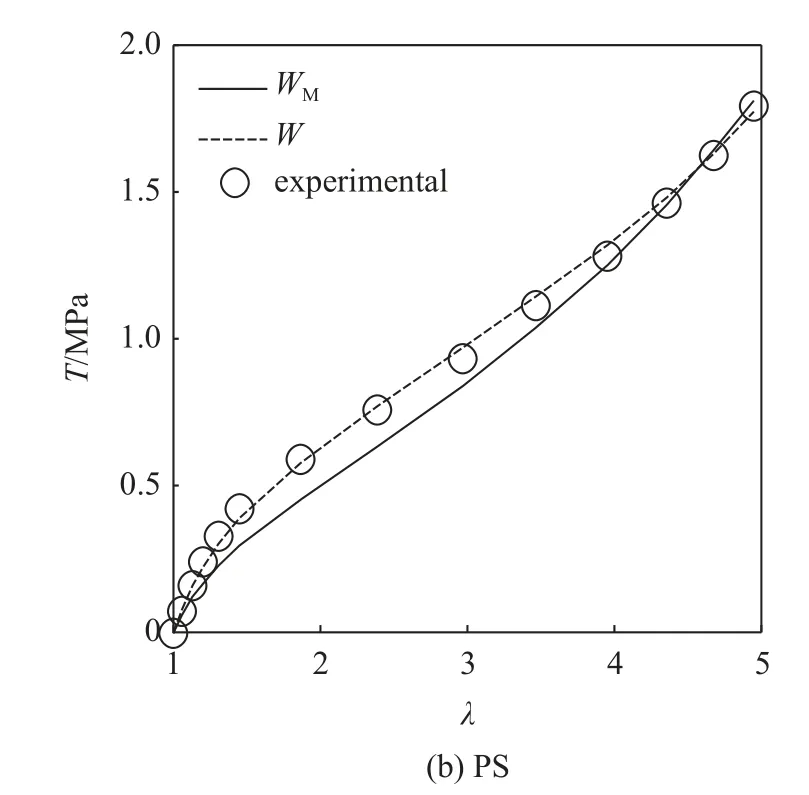
图9 Mansouri 模型对不同变形模式实验数据的预测效果(续)Fig.9 Predicted effect of the Mansouri model for experimental data of different deformation modes(continued)

4 结论

本文基于Treloar 的实验数据,开展了超弹性材料的完全本构关系研究.首先研究了单轴拉伸、等双轴拉伸和纯剪切3 种变形模式的本构理论,再采用以I1和I2为底的非指定指数幂函数作为基本应变能函数,通过3 种模式下全范围实验数据的总体误差泛函寻优,识别得到相应的本构参数,预测精度比已有工作更高.

本文所采用的应变能函数形式及其参数识别方法具有一般性,因而适用于其他超弹性材料(例如n-苯基-2-萘胺硫化橡胶,参考附录)完全本构关系的建立.我们的实践还表明,本文提出的基于多变形模式实验数据及其两阶段的研究策略,也适用于采用Ogden 型等其他函数类型建立超弹性材料的完全本构关系.

附录 n-苯基-2-萘胺硫化橡胶的完全本构关系

根据文献[26,31]中的实验曲线,提取得到n-苯基-2-萘胺硫化橡胶的单轴拉伸(ST)和纯剪切(PS)实验数据,分别如附表1和附表2 所示.

附表1 单轴拉伸实验数据Table A1 Experimental data under the ST state

附表2 纯剪切实验数据Table A2 Experimental under the PS state

根据本文提出的方法,可以确定伸长比不超过1.2 的7 组实验数据为初始阶段.

在非常小变形情形下,超弹性材料都服从neo-Hookean模型,即

根据式(10),并结合初始阶段数据,得到7 个数据的误差分别为

定义该阶段的总体误差泛函为

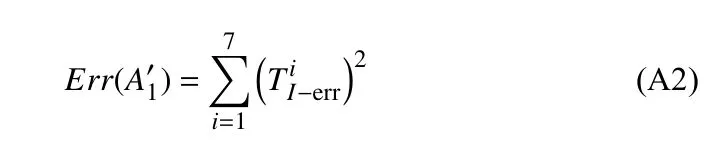
通过对总体误差泛函Err() 关于本构参数求变分,解析得到=0.178 2,进而得到初始剪切模量[14]G=2=0.356 5 MPa.

将两种变形模式实验曲线除初始阶段的剩余部分作为第2 阶段进行统一处理.考虑到已得到材料在初始阶段的本构特性,通过得到两种模式全变形范围的更新实验数据TU-E′.

接下来,依据TU-E′数据,研究剩余阶段的本构特性,为此,假设应变能函数为

根据单轴拉伸和纯剪切的本构关系,针对式(A3)的应变能函数,得到不同模式的本构关系为构造两种模式的总体误差泛函,最后运用1stOpt 软件,在总体误差泛函为Err=0.031 44 时识别得到模型参数为

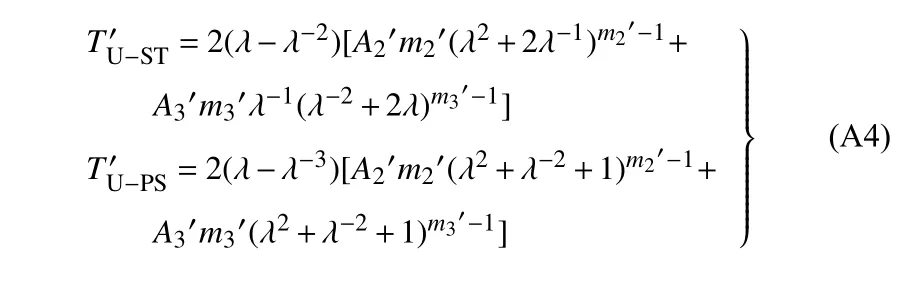
于是得到该材料的总体应变能函数为

仅为0.03144 的总体误差泛函表明,利用本文方法建立的完全本构关系,反映了n-苯基-2-萘胺硫化橡胶材料的实际变形特性.