左旋寻常的极光千米波与辐射带高能电子相互作用的参数化研究*
李文涛 张赛 贺佳贝 邓舟坤 杨奇武 商雄军 周庆华
1(长沙理工大学物理与电子科学学院 长沙 410114)
2(中国科学院空间天气学国家重点实验室 北京 100190)
3(腾讯云计算(长沙)有限责任公司 长沙 410221)
4(湖南省普通高校重点实验室 近地空间电磁环境监测与建模实验室 长沙 410114)
0 引言
极光千米波(Auroral Kilometric Radiation,AKR)是地球磁层等离子体中相速度大于光速的电磁波,频率在30~800 kHz,功率可达107~109W[1-3]。目前,普遍认为极光千米波是来自磁尾的超热电子(能量1~10 keV)在极区由于电子回旋注入不稳定性ECMI(Electron Cyclotron Maser Instability)激发的[4]。空间等离子体中的极光千米波存在三种模式,即右旋奇异(Right-hand Extraordinary,R-X)模、左旋寻常(L-O) 模和左旋奇异(Left-hand Extraordinary,L-X)模。极光千米波的产生机制预测地球磁层中的极光千米波主要以R-X 模为主,很多观测数据也证实了这一点[4-8]。Summer等[9]研究了第一阶共振驱动的极光千米波与辐射带电子的相互作用,结果表明极光千米波能够对高能电子产生明显加速效应。随后,Xiao等[10]构建了包含波磁场分量的极光千米波局地扩散系数表达式。在此基础上,Xiao等[11,12]随后使用假设的极光千米波磁场分量参数,计算了由15 阶共振驱动的极光千米波弹跳平均扩散系数,结果表明极光千米波能在一天内对电子产生有效加速,甚至能将电子能量加速至约100 倍,而这些被加速的电子有可能严重威胁航空系统及空间天气。
由于极光千米波的源区位于高度为1~3Re的高纬极光区[1,3,13],因此早期对极光千米波的观测主要集中在高纬区域。2015 年Kurth等[14]基于Van Allen 探测器的数据报道了辐射带低纬区域的极光千米波,说明产生于极区的极光千米波能够出现在辐射带甚至赤道附近。Xiao等[15]利用3D 射线追踪方法研究了不同地磁条件下极光千米波的传播,证明在一定条件下极光千米波可以从高纬极区传播至低纬区域甚至赤道区域。2019 年基于Van Allen 探测器数据的统计结果表明,辐射带的极光千米波存在于L为3~6.5 和整个磁地方时的广泛区域[16,17]。
由于缺乏高频电磁波磁场分量的观测数据和其他判断电磁波极化的手段,之前对极光千米波的传播机制及其与电子相互作用的研究主要是基于极光千米波为R-X 模的假设。虽然Hanasz等[18]2003 年在使用Interball-2 数据研究极光千米波发生率分布的工作中发现磁层高纬区域存在L-O 模,但是辐射带的中低纬区域长期以来没有关于L-O 模的报道,因此关于辐射带中L-O 模与电子之间的相互作用尚未被系统性研究。2018 年Nakamura等[19]利用Arase 卫星观测数据报道了极光千米波极化的研究事例,发现在辐射带中不仅存在R-X 模,同时也存在L-O 模。基于此,本文通过改变L-O 模的峰值频率(ωm)、传播角(θ)分布和纬度(λ)分布,计算电子弹跳平均扩散系数,参数化研究L-O 模与外辐射带高能电子的相互作用。
1 模型介绍
在忽略离子运动及无碰撞的冷等离子体时,高频斜传播的L-O 模的色散关系为[9,10,20]
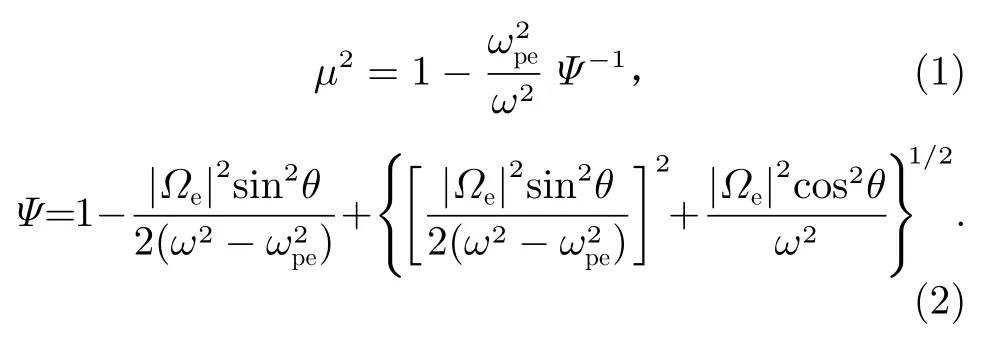
其中,µ为等离子体的折射率,ω为波的角频率,ωpe为电子等离子体频率,Ωe为电子回旋频率,θ为波传播角。根据波的色散关系得到L-O 模的下截止频率为
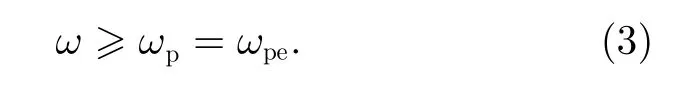
电磁波与电子之间的n阶谐波回旋共振条件为
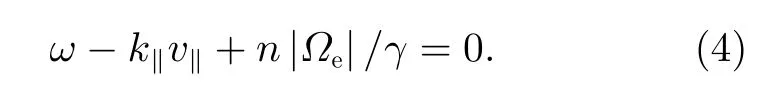
其中,k‖=kcosθ为波的平行波数;v‖=vcosα,v为电子速度,α为电 子投掷角;γ为洛伦兹因子。由于极光千米波为超光速波,由其定义可知相速度u=ω/k >c,回旋共振阶数n只能取负值-1,-2,-3,···,∞。
在描述波粒相互作用的准线性扩散方程中,弹跳平均的投掷角扩散系数、动量扩散系数和交叉投掷角扩散系数<Dαα>,<Dpp>,<Dαp>=<Dpα>具体形式为[21,22]
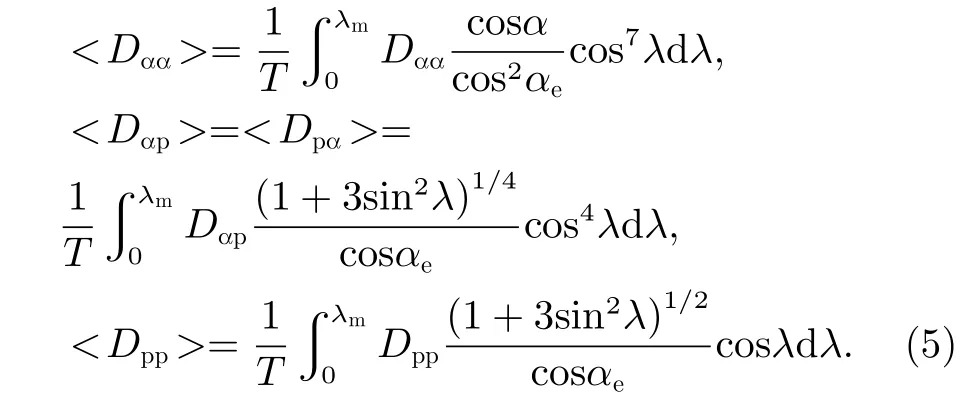
式中,归一化的弹跳时间可以通过T(αe)≈1.30-0.56sinαe得 到,这里αe为 电子赤道投掷角;λm为L-O模存在的最大纬度,Dαα,Dpp,Dαp=Dpα分别为局地的投掷角扩散系数、动量扩散系数及交叉投掷角-动量扩散系数,其均具有与p2/t相同的量纲[22-24]。局地扩散系数矩阵D的每个元素均可以表示为一个在波的传播角范围内对X(X=tanθ)的积分和对所有共振阶数n的求和,即
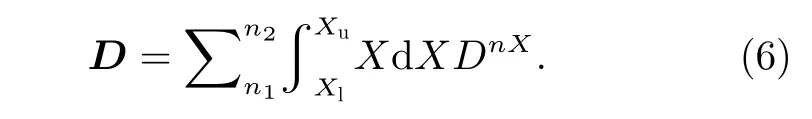
其中,Xl为 传播角正切值的下限,Xu为传播角正切值的上限,并满足高斯分布。
根据以往研究[10]可以求得投掷角扩散系数
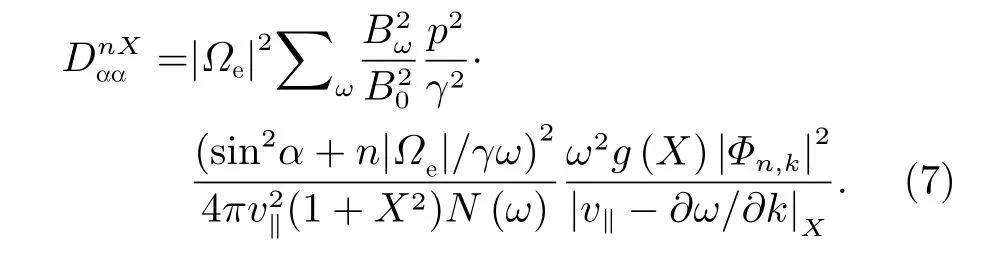
其中,B0为背景磁场强度,ω取所有共振频率,|Φn,k|2与 波的色散关系相关,N(ω)则是一个使得每单位频率的波能量等于的归一化因子,后两个量在之前的研究中已经得到[22,25]。而交叉及动量局地扩散系数与的关系如下:

2 数值结果与分析
此前对极光千米波的研究表明,在一定条件下极光千米波能够从高纬极区传播进入辐射带的低纬区域,甚至到达低纬赤道附近。在这些区域,辐射带中的高能电子会与极光千米波发生回旋共振,这可能引起高能电子的显著加速,从而导致空间天气灾害的发生。Xiao等[11]曾针对R-X 模的极光千米波对辐射带电子的动力学演化进行了系统的参数化研究。以此为参考,这里通过计算L-O 模在不同的峰值频率(ωm)、传播角(θ) 分布和波纬度(λ)分布情况下,辐射带电子的弹跳平均扩散系数,对L-O 模与辐射带电子的相互作用进行参数化研究。
分析中假设是在强磁暴(KP=5)期间的 L-O 模与高能电子发生阶数n为-1~15 的回旋共振作用,其发生区域为L=4.5 的外辐射带区域。在磁暴发生期间,等离子层顶会向地球压缩,导致所选区域的等离子体密度变低(这里选取的等离子体密度参数ωpe2/Ωe2=2.0,电子数密度n0=ωpe2ε0me/e2=2.0Ωe2ε0me/e2,其中ε0为 介电常数,me为电子质量,e为电子电荷量值)[26];极光千米波的波幅度在磁暴时可以达到0.1 nT 左右[27],这里选取L-O 模的幅度Bt=0.1 nT。根据既有研究结果,极光千米波的传播路径十分倾斜[9,28],且目前缺少辐射带关于极光千米波传播角的具体观测数据。为使模拟结果更加准确,这里选取较大的 L-O 模传播角范围作为计算扩散系数的参数。采用的参数具体如下:Xl=tan5°,Xu=tan89°,Xm=tan60°,Xω=tan50°。选择的频率参数为ωl/(2π)=10 kHz,ωu/(2π)=500 kHz,δω/(2π)=100 kHz。同时假设L-O 模存在于沿着整个磁场线的所有纬度,具有恒定的波幅Bt=0.1 nT。
2.1 波的不同峰值频率对辐射带电子的影响
为研究峰值频率ωm对L-O 模与辐射带电子相互作用的影响,分别考虑ωm/(2π)=150 kHz,250 kHz和350 kHz三种情况。
从图1 中可以明显发现,当峰值频率为150 kHz时,1 MeV 以下能量电子的有效扩散系数(> 10-9s-1)覆盖了整个投掷角范围,扩散系数随着电子能量的增加而逐渐减小。随着波的峰值频率从150 kHz 增大到350 kHz,投掷角、动量以及交叉扩散系数覆盖的投掷角区域逐渐减小。同时,从图1 中可以得知,对于三种峰值频率的L-O 模与电子相互作用,有效的动量扩散系数覆盖的投掷角范围均大于投掷角扩散系数覆盖范围。
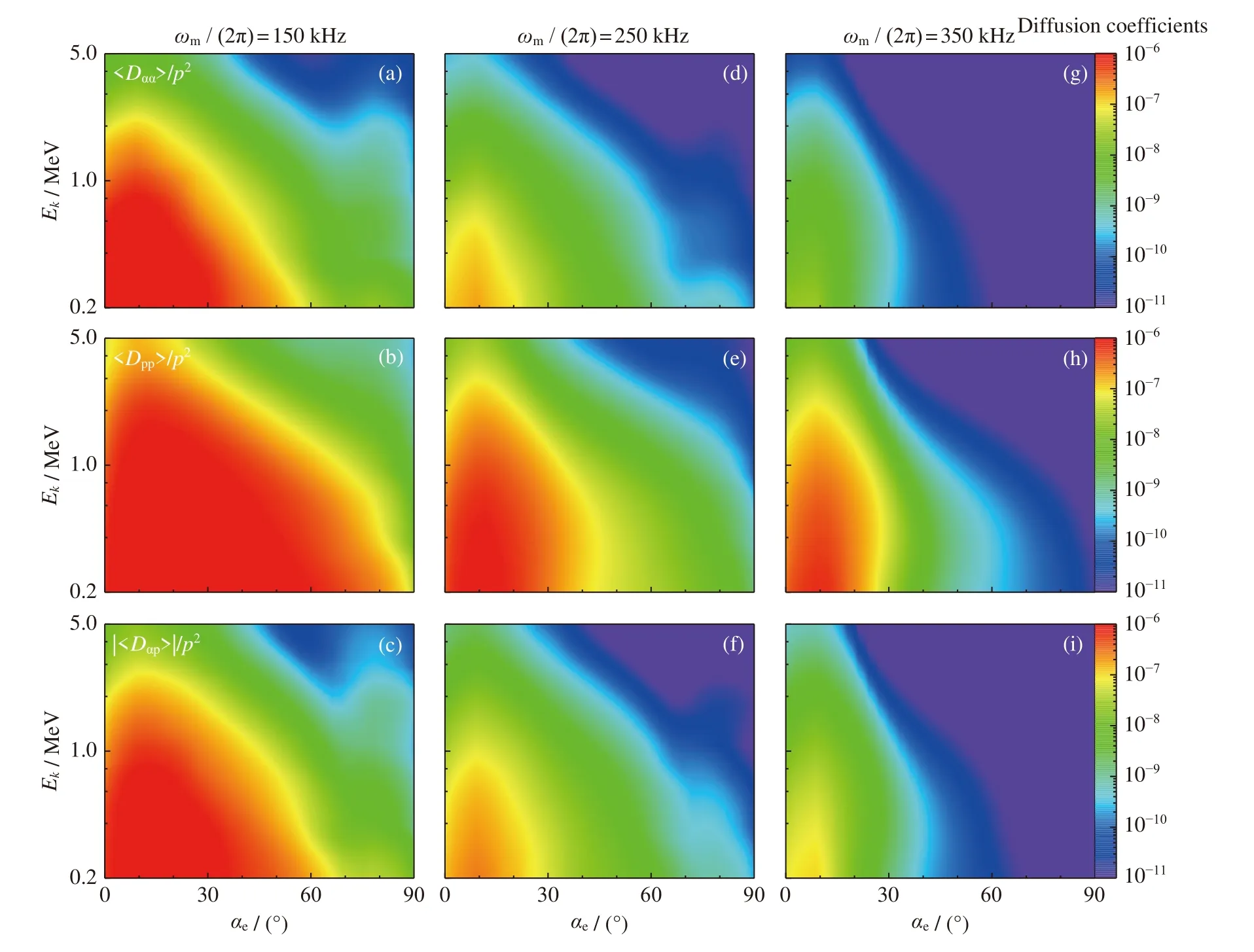
图1 不同峰值频率的投掷角(上)、动量(中)及投掷角-动量交叉(下)弹跳平均扩散系数2D 结果Fig.1 2D bounce-averaged diffusion coefficients of pitch angle (top),momentum (middle),and cross (bottom)
图2 表明,在小投掷角区域(< 30°),峰值频率为150 kHz 的L-O 模对1 MeV 的电子,动量扩散系数比投掷角扩散系数约高10 倍;但是在大投掷角处(> 60°),动量扩散系数比投掷角扩散系数高约100 倍,这说明L-O 模对电子的主要作用是导致其动量扩散,因此L-O 模具有加速电子的可能。图3 给出了1 MeV 能量电子的投掷角扩散系数与动量扩散系数的对比,研究表明,对于这三种不同峰值频率的L-O 模,扩散系数均随投掷角的增大而下降,特别是在峰值频率为250 kHz 和350 kHz 时,随着投掷角的增大,扩散系数的下降更为迅速。此外,对比分析三种频率的扩散系数,可以发现弹跳平均扩散系数会随着峰值频率的增加而降低。这是因为在其他条件不变的情况下,L-O 模与电子共振时,共振频率大多集中在较低频率且不会随峰值频率变化,当峰值频率增加时,这些共振频率会越远离峰值频率,共振能量将减弱,使得扩散系数减小,这与R-X 模的情况较为相似[11]。

图2 不同峰值频率的投掷角(上)、动量(中)及投掷角-动量交叉(下)弹跳平均扩散系数1D 结果Fig.2 1D bounce-averaged diffusion coefficients of pitch angle (top),momentum (middle),and cross (bottom)
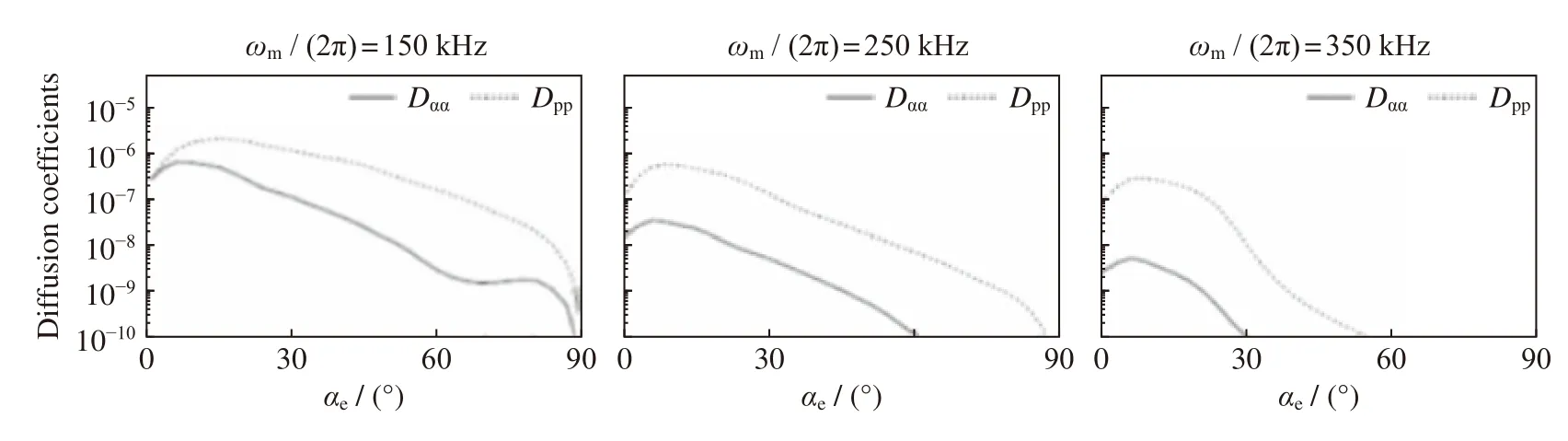
图3 能量为1 MeV 的投掷角扩散系数(Dαα)与动量扩散系数(Dpp)的对比Fig.3 Comparison of the pitch angle diffusion coefficient (Dαα) and momentum diffusion coefficient (Dpp) with energy of 1 MeV
2.2 波的不同传播角分布对辐射带电子的影响
此前针对准线性散射率对亚光速合声波传播角分布情况的敏感性研究发现,散射率对高能量波的传播角分布相对不敏感[29]。2007 年Xiao等[28]基于射线追踪技术针对极光千米波传播路径的研究发现,极光千米波初始传播角的不同会在一定程度上影响其传播路径。
为研究不同传播角对L-O 模与辐射带电子间相互作用的影响,选取了4 组不同L-O 模传播角分布范围进行计算与分析。这4 组范围分别是:完整传播角范围5°<θ<89°,中等及大的传播角范围25°<θ<89°,大传播角范围45°<θ<89°,中等传播角范围45°<θ<65°。计算采用的波的传播角参数均与2.1 节中一致。在4 种传播角范围的计算中采用的L-O 模峰值频率均为ωm/(2π)=150 kHz。
图4 给出的是在4 种不同L-O 模传播角分布情况下的二维电子弹跳平均扩散系数。从情况1~3 可以明显看出,在最小传播角不同而最大传播角相同的条件下,三种情况之间的扩散系数没有明显差异。图4 中,情况4 采用的最小传播角与情况3 是一致的,最大传播角则与前三种情况不同,但是可以发现情况4 的扩散系数与前三种情况未发生较大变化,因此可从图4 中得到在峰值传播角及半宽带不变的情况下,传播角范围对L-O 模与电子相互作用的扩散系数影响很小。
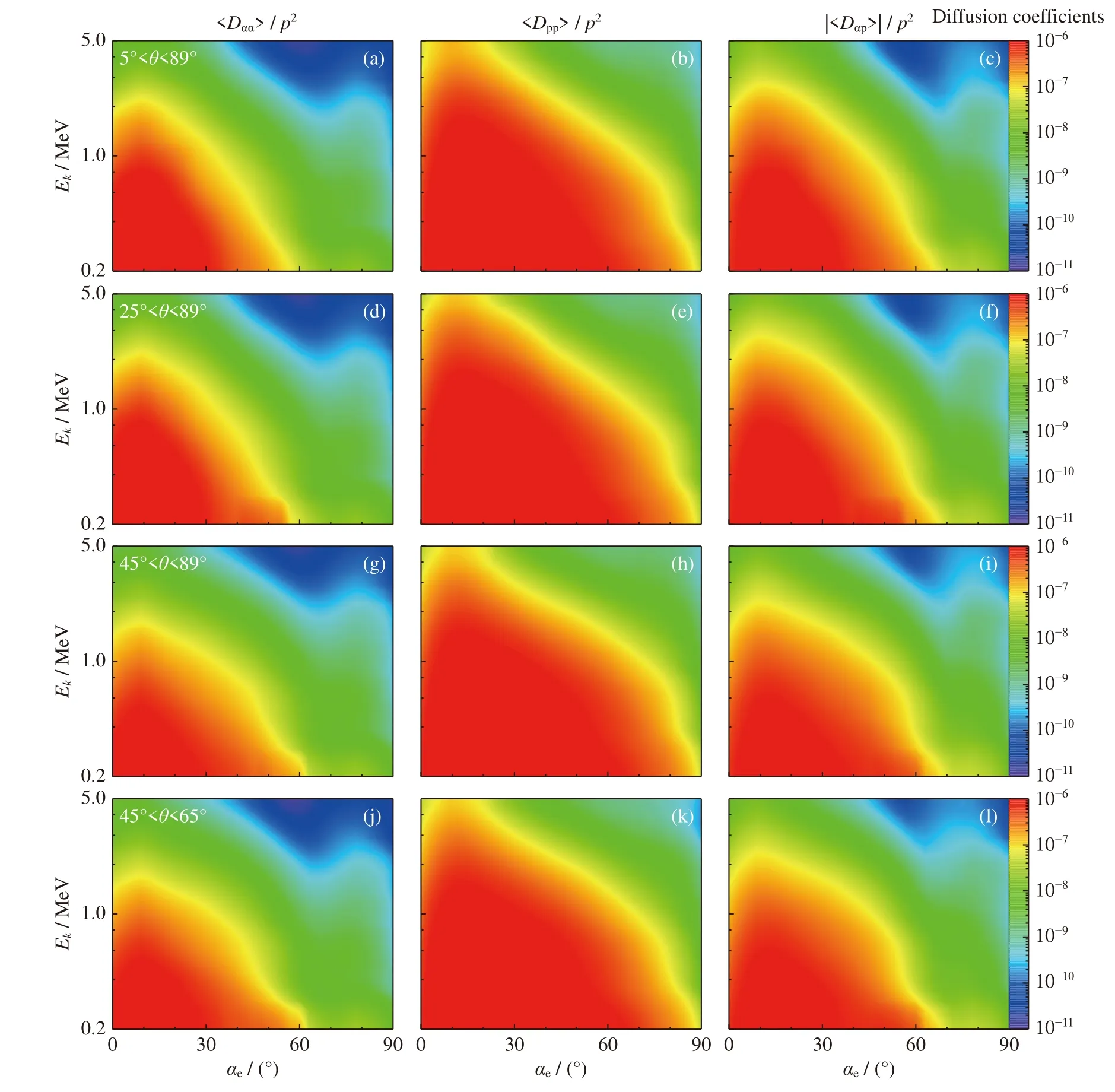
图4 不同传播角分布的投掷角(左)、动量(中)及投掷角-动量交叉(右)弹跳平均扩散系数2D 结果Fig.4 2D bounce-averaged diffusion coefficients of pitch angle (left),momentum (middle),and cross (right) for different wave normal angle distributions
图5 是与图4 对应的一维扩散系数,与图4 类似,在最小传播角不同而最大传播角相同的条件下(情况a~c),三种情况的扩散系数没有明显差异。在最大传播角变小后(情况j~l),扩散系数相比前三种情况同样未发生明显变化,同样也能说明在峰值传播角及半宽带不变的情况下,L-O 模与电子相互作用的扩散系数对传播角范围的依赖较弱。
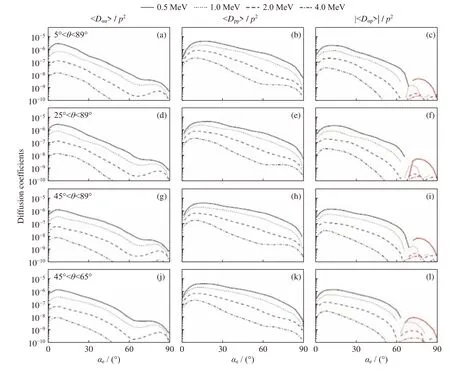
图5 不同传播角分布的投掷角(左)、动量(中)及投掷角-动量交叉(右)弹跳平均扩散系数1D 结果Fig.5 1D bounce-averaged diffusion coefficients of pitch angle (left),momentum (middle),and cross (right)for different wave normal angle distributions
2.3 波的不同纬度分布对辐射带电子的影响
既有研究结果表明,波存在的纬度分布会影响其与粒子之间的相互作用[30,31],R-X 模对电子的动力学影响会随着纬度的不同而发生变化,高纬的R-X 模会导致电子投掷角散射,而在赤道附近或者低纬处,则会有效加速电子[32-34]。
为了探究不同纬度分布对L-O 模与辐射带电子相互作用的影响,同样选择三个具有代表性的L-O 模纬度分布范围计算扩散系数:所有纬度区域(λ>0°),中高纬度区域(λ>20°),高纬区域(λ>40°)。在此计算中采用的L-O 模的峰值频率同样为ωm/(2π)=150 kHz。
图6 给出的是在三种不同L-O 模纬度分布情况下,电子二维弹跳平均投掷角、动量及投掷角-动量交叉扩散系数。从图6(a)~(c)可以清晰发现,在纬度分布为所有纬度区域时,有效扩散系数覆盖了整个投掷角范围。然而随着纬度分布变为中高纬区域后,扩散系数会移动到较小的投掷角区域(<60°)如图6(d)~(f)所示。到了高纬区域时,扩散系数只存在于30°以内的投掷角区域,如图6(g)~(i)所示。同时,随着波存在纬度范围的减小,扩散系数会有一个数量级左右的减小。
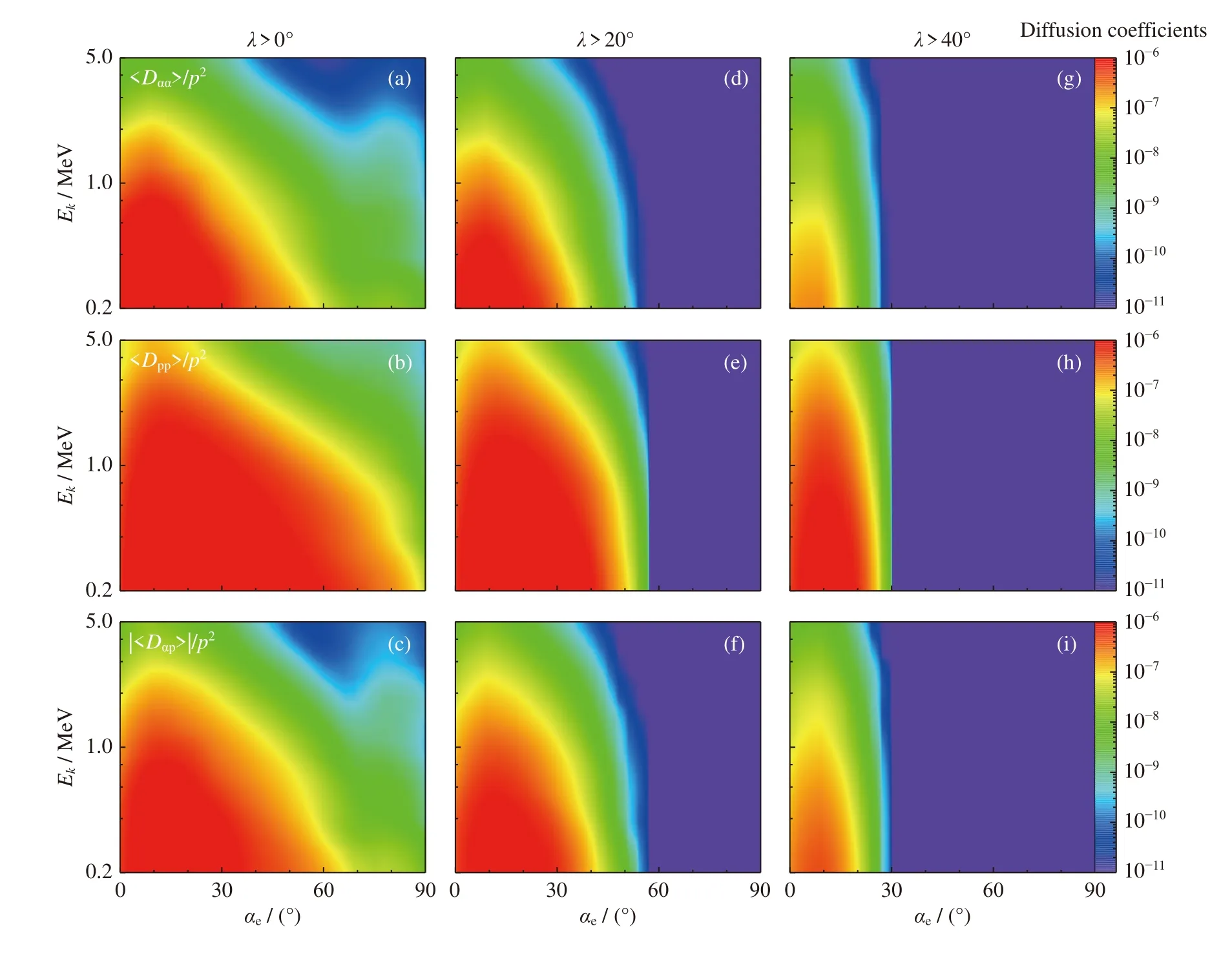
图6 不同纬度分布的投掷角(上)、动量(中)及投掷角-动量交叉(下)弹跳平均扩散系数2D 结果Fig.6 2D bounce-averaged diffusion coefficients of pitch angle (top),momentum (middle),and cross (bottom) for different wave latitudinal distributions
图7 是与图6 对应的不同能量电子的一维扩散系数。如图7(a)~(c)所示,当纬度分布为整个纬度区域时,在整个投掷角区域中,扩散系数变化较为平缓。但是在中高纬度区域,扩散系数在投掷角为50°附近会急剧下降,如图7(d)~(f)所示。而在高纬区域,在投掷角为25°时扩散系数急剧下降,如图7(g)~(i)所示。这说明纬度分布对L-O 模与电子之间的相互作用有着较大影响,L-O 模存在的纬度变化会导致电子动力学过程发生剧烈变化。
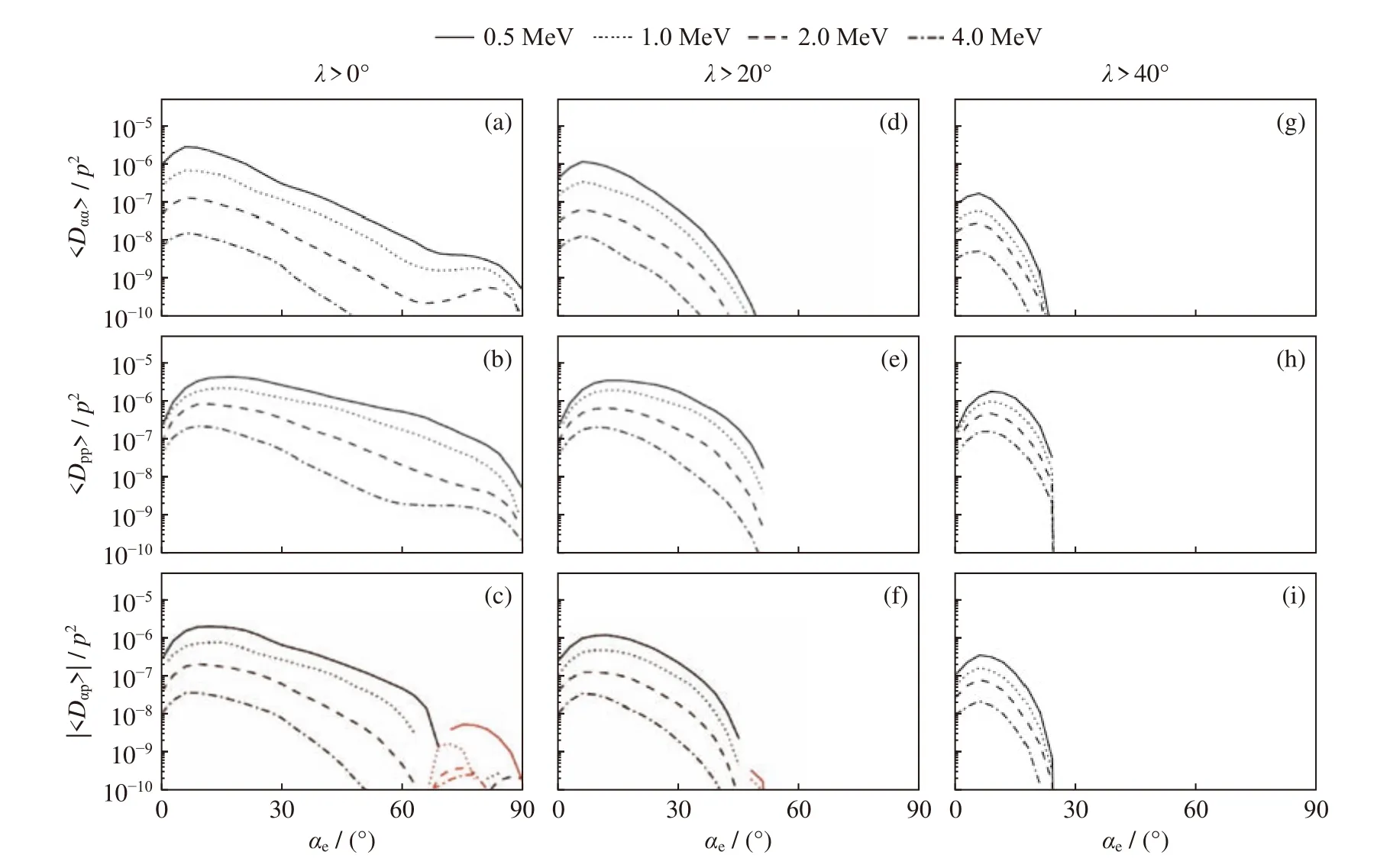
图7 不同纬度分布的投掷角(上)、动量(中)及投掷角-动量交叉(下)弹跳平均扩散系数1D 结果Fig.7 1D bounce-averaged diffusion coefficients of pitch angle (top),momentum (middle),and cross (bottom) for different wave latitudinal distributions
3 结论
通过使用L-O 模3 组不同的峰值频率参数、4 组不同的传播角分布参数以及3 组不同的纬度分布参数,分别计算了电子弹跳平均的投掷角、动量及投掷角-动量扩散系数,探讨了不同参数的L-O 模对辐射带中高能电子的影响。得到结论如下。
(1)随着L-O 模峰值频率的增加,有效扩散系数覆盖的投掷角范围会逐渐减小,并且扩散系数也会逐渐减小。这可能是由于对电子弹跳平均扩散系数的影响主要来自波高斯分布的峰值频率附近的根,而共振频率大多集中在较低的波频率附近。此外,动量扩散系数均大于投掷角扩散系数与交叉扩散系数,最大高出约100 倍,这说明L-O 模对电子的主要影响是导致其动量扩散,也证明L-O 模可能会对电子进行有效加速。
(2)在L-O 模的峰值传播角及半宽带不变,最大传播角相同时,其与电子相互作用的扩散系数之间没有明显差异。在最大传播角相同而最小传播角不同时,扩散系数同样没有发生较大变化,说明L-O 模与电子相互作用的扩散系数与传播角范围之间没有很密切的联系。
(3)当纬度分布为整个纬度区域时,在所有投掷角范围内,扩散系数的变化较为平缓。但是在纬度分布为中高纬区域时,扩散系数在投掷角50°附近会急剧下降。而在高纬区域,在投掷角为25°时扩散系数急剧下降。这说明纬度同样会对L-O 模与电子之间的相互作用造成较大影响,L-O 模的纬度分布变化会对其与电子的相互作用过程发生显著影响。
需要指出的是,Denton等[35]2002 年的研究工作发现,电子密度沿磁力线会随纬度的升高而增加,在L=4.5 的磁力线上,L-O 模分布的维度范围内电子密度变化不大(例如纬度50°处的电子密度是赤道处的1.76 倍)。在采用上述计算参数的情况下,场向密度变化对扩散系数的影响较小。为突出L-O 模的频率、传播角和分布纬度等特性在与电子相互作用中的影响这一重点,同时也为了减少计算量,这里没有讨论场向密度变化对扩散系数的影响,这方面研究将在今后工作中开展。同时,计算采用了假设的波谱参数,进一步的工作将基于卫星对L-O 模波的观测数据,研究其与辐射带电子的相互作用。

