IMF 北向时太阳风粒子向磁层输运的试验粒子模拟研究*
赵明现
(中国气象局空间天气重点开放实验室/国家卫星气象中心(国家空间天气监测预警中心) 北京 100081)
(许健民气象卫星创新中心 北京 100081)
0 引言
太阳风和行星际磁场(IMF)与地球内禀磁场相互作用,形成了向阳面被压缩、背阳面被拉伸的地球磁层。磁层中的等离子体主要有内外两个来源,内源为电离层,外源为太阳风[1]。一般来说,太阳风等离子体对磁层中的远地区域起支配作用,而来自电离层的粒子对磁层中的近地区域起主导作用[2,3]。
太阳风等离子体向磁层输运是太阳风-磁层相互作用的一个重要过程,对这个过程物理机制的探讨一直是一个重要的研究方向。Dungey[4]提出的磁场重联机制是目前普遍接受的一种理论,在向阳面磁层顶日下点发生磁场重联,从而剥离向阳面磁层中的磁力线,并将之拖向背阳面磁尾。日下点的磁场重联受IMF 控制,IMF 南向时的重联率要显著的高于IMF北向时[5],此时太阳风粒子主要通过晨侧磁层顶直接进入磁层中的等离子体片和环电流区域[2]。在IMF北向期间,磁重联发生在高纬的南北极尖区背阳面一侧[6,7],这个过程会在向阳面磁层中形成新的闭合磁力线,闭合磁力线携带太阳风粒子沉入磁层内部,并沿方位角方向往晨昏两侧形成低纬边界层(Low Latitude Boundary Layer,LLBL)。此 外,IMFBx和By在太阳风-磁层能量耦合过程中也起着重要的作用,同样条件下IMF 径向时进入磁层的能量比IMF北向时要大[8]。
Axford 和Hines[9]提出,太阳风与磁层顶侧面等离子体的黏性相互作用会在磁层中形成对流,从而使太阳风动量传入磁层内。这种机制不受IMF 方向的影响,不过对太阳风向磁层的能量传输贡献并不大,大概在10%~20%[10]。K-H 不稳定(Kelvin-Helmholtz Instability,KHI)也是一种可能的传输机制。观测表明,在低纬的晨昏两侧,太阳风等离子体相对于磁层顶内的等离子体具有很高的速度,K-H 波在边界层会形成局地的小尺度涡旋[11,12]。虽然具体的物理过程尚无定论,但是从卫星观测数据分析,在IMF 北向时,磁尾晨昏两侧的KHI 会导致磁鞘中的太阳风向磁层内的传输[13]。另外,磁鞘中的动力阿尔芬波也能让磁鞘等离子体进入磁层[14,15],如果磁鞘中存在动量足够大的不均匀结构体,也可以直接穿过磁层顶进入磁层[16,17]。不同的传输机制之间并不互斥,在实际的物理过程中,可能同时起作用[18]。
试验粒子方法已经在空间物理和天文学中得到广泛的应用,常用于日地空间中粒子的起源、传播和损耗等过程的研究。试验粒子法需要给定背景场,包括电场和磁场等,通过跟踪单个或多个粒子的动力学过程,来研究复杂系统中的物理过程。由于不考虑试验粒子对背景场的反馈以及各试验粒子之间的相互作用,所以这个方法是不自洽的。但是在研究大尺度的复杂问题时,自洽模型会带来巨大的运算量,而作为系统一阶近似的试验粒子方法足够研究很多粒子的动力学问题,是大尺度磁流体模拟的有益补充[19]。也可以在计算试验粒子轨道时,使用时间回推方法,研究粒子起源[20]。
试验粒子法又可以分为粒子轨道法、蒙特卡罗法等[19],粒子轨道法通过单个粒子或一群粒子的运动轨道,来研究系统中的粒子输运过程,本文研究使用的是试验粒子轨道法。Speiser[21]使用试验粒子轨道法基于Dungey 磁层模型研究了太阳风粒子向磁层电流片中的输运和极光粒子的加速,但其使用的磁层背景场设定太过简化,与真实物理过程相去甚远。Delcourt[22]通过单粒子的轨道变化研究了磁层中氧离子在地磁亚暴期间的加速过程。Li等[23,24]研究亚暴期间能量粒子注入磁层的过程,Tang等[25]对磁暴期间能量粒子进入磁层做了数值模拟研究,这些研究着重于能量粒子,而不是能量较低的太阳风粒子。Moore等[2]使用四阶龙格库塔方法求解全洛伦兹方程,以LFM 磁层模型的磁流体(MHD)模拟结果为背景场,研究了太阳风和极区电离层向磁层中的粒子输运特征,不过其所使用的MHD 背景场是选择了IMF 南向和北向两个时刻,是固定的背景场,此外该MHD模拟并未考虑地磁轴倾角的影响。Ding[3,26]使用试验粒子法模拟计算了太阳风粒子向磁层等离子体片的输运,背景场使用BATS-R-US 的MHD 模拟结果,背景场随时间变化且考虑了地磁倾角,不过MHD 模拟使用的是人工设定的理想太阳风条件,并非实际观测得到的太阳风数据,另外粒子轨道的计算采用了引导中心近似,而引导中心近似方法得到的粒子运动轨迹与全洛伦兹方程相比会存在一定的误差[3]。Guo等[27]基于自主开发的磁层MHD 模型和试验粒子法,研究了磁尾等离子体片的粒子注入机制,其中磁层背景是给定行星际条件下计算得到的稳态结果,通过对19600 个粒子的追踪,讨论了一些典型的粒子运动轨迹。Cao等[28]研究了非磁暴期间IMF 南向时太阳风粒子向磁层的注入,不过对IMF 北向的情景,只讨论了单个粒子的运动轨道特征,没有做大规模粒子运动的模拟研究,而且使用的BATS-R-US 磁层MHD 模拟结果是理想太阳风状况下的稳态结果,不随时间变化。
本文以ACE 卫星实时观测数据驱动的BATSR-US 全球MHD 模拟为背景场,使用试验粒子法对北向IMF 时太阳风粒子向磁层中的输运过程进行模拟,研究北向IMF 时太阳风粒子注入磁层的过程以及粒子在磁层中的分布特征。
1 数值模拟方法
虽然使用固定的(或人工设定的随时间变化的)行星际参数驱动磁层MHD 模型可以得到IMF 北向时的磁层状态[3,26,28],但是使用卫星实时观测的太阳风和IMF 参数作为驱动,并将磁倾角等参数设定为实际数值,得到的MHD 模拟结果会更加接近实际情况。在2003 年10 月22-24 日,有一次持续时间较长的北向IMF 事件,ACE 卫星观测的太阳风和IMF数据如图1 所示。选用2003 年10 月22 日00:00 UT作为太阳风-磁层MHD 模拟的起始时间,每4 min保存一次MHD 模拟结果。通过对空间进行三维插值,可以求得模拟区域内任意位置的MHD 背景场参数,再通过线性时间插值,就可以得到一个随时间变化的太阳风-磁层相互作用的背景场。太阳风-磁层MHD 数值模拟通过CCMC(Community Coordinated Modeling Center)*https://ccmc.gsfc.nasa.gov/实现,磁层模型选用BATS-R-US。

图1 2003 年10 月22-25 日ACE 卫星观测到的太阳风和IMF 数据Fig.1 ACE satellite observation data on 22-25 October 2003
在研究磁层粒子分布时常以离子为对象,这是因为电子具有更复杂多样的起源机制,并且很难区分电子的来源[3]。太阳风中的离子主要是质子,所以本文以质子为追踪粒子,研究太阳风粒子向磁层输运的过程。带电粒子在行星际和磁层中的运动可以用以下洛伦兹方程来描述:
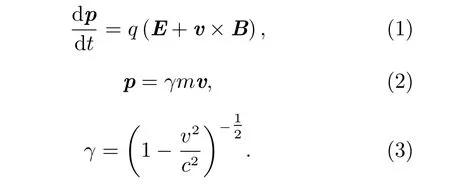
其中,q和m为 粒子电荷和质量,v为粒子速度,p为粒子动量,γ为洛伦兹因子,c为真空光速,E和B分别为粒子所在位置的电场强度和磁感应强度,其之间满足E=-vMHD×B,这里vMHD为磁流体速度。
在满足绝热近似的条件时,可以用引导中心近似的方法描述粒子的运动轨迹,这样可以将求解6 个未知量的洛伦兹方程简化为求解4 个未知量的引导中心近似方程,同时引导中心近似方法也使得求解时可以使用更大的时间步长,从而大大地降低运算量,但是与全洛伦兹方程相比,引导中心近似方法得到的粒子运动轨迹会存在一定的误差[3],而且由于使用了绝热条件,所以并不能反映粒子的加热过程。本文选用4 阶龙格库塔方法求解全洛伦兹方程以得到粒子运动轨迹,并使用变时间步长的方法,根据粒子的回旋周期,自动调整时间步长。时间步长的选择也会对粒子的运动轨迹造成影响。Ding[3]使用引导中心近似求解中,认为应该将时间步长设置为约1/10 个回旋周期,对于全洛伦兹方法,则需要更小的步长。Peroomian 和EI-Alaoui[29]认为求解高能粒子的全洛伦兹方程时应该将步长设置为离子回旋周期的0.002 倍。Birdsall 和 Langdon[30]认为时间步长应该设定为εP/F,其中P为粒子动量,F为洛伦兹力,ε为一个预设很小的值[31]。Pulkkinen等[32]认为时间步长可以设定为粒子回旋周期的约1/180。
为了选择合适的时间步长,对单个粒子设定不同时间步长,比较其运动轨迹的差异。选择一个稳态的BATS-R-US 模拟结果作为背景场,粒子初始位置位于磁层内部,坐标为(8.80,0.04,1.99)Re(Re为地球半径)。粒子初始速度接近所在位置的磁流体速度(-228.4,70.5,206.8)km·s-1。分别计算时间步长 Δt为(1/20)T,(1/50)T,(1/100)T,(1/200)T(T为质子所在位置的回旋周期)时质子的运动轨迹,质子位置坐标的存储时间间隔为1 s,质子运行轨迹如图2 所示。Δt=(1/20)T时,质子的轨迹与其他情况相比差异明显,其位置超出模拟区域的时间(逃逸时间)为30917 s。Δt=(1/50)T时,运动轨迹与(1/100)T相比在磁尾区域稍有差异,其逃逸时间为43898 s。Δt=(1/100)T和 Δt=(1/200)T两种情况的质子运动轨迹非常接近,其逃逸时间分别为44548 s 和44352 s。综合考虑计算精度和计算量,在本文的大规模粒子模拟中,时间步长设定为(1/100)T。
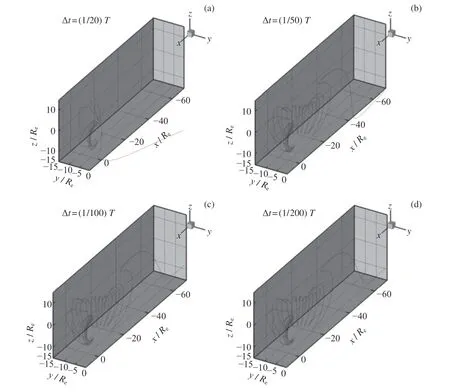
图2 使用不同时间步长计算得到的粒子运动轨迹Fig.2 Trajectories of a single particle using different settings of time step
2 数值模拟结果
CCMC 得到的太阳风-磁层MHD 背景场使用的是非均匀网格,为了提高插值运算速度,先将所有时刻的背景场插值转换为间隔为1Re的均匀网格。背景场采用GSM 坐标系,在x方向的范围为(-80~20)Re,在y和z方向的范围均为(-40~40)Re。试验粒子数量为107个,入射位置随机分布于x=19Re的平面上,粒子入射初始速度由观测数据插值计算得到,温度设定为 10 eV,热速度满足麦克斯韦分布。初始时每秒入射104个,后续逃逸出模拟区域的粒子放在入射位置重新注入模拟区域。由于每次入射的粒子数量会存在差异,所以对每次的入射粒子均会赋予一个权重系数,从而使得折算后的粒子密度接近于实际的太阳风粒子密度。权重系数的关系式为

其中,W(t)为t时刻入射粒子的权重系数,n(t)为t时刻太阳风粒子数密度,A为入射位置的截面面积,N(t)为t时刻的入射粒子个数。
每隔100 s,输出一次试验粒子分布的计算结果。将模拟区域内的每个粒子,按其权重系数和粒子所在网格中的位置与网格顶点的距离,线性分配给网格的8 个顶点。每个格点周围的粒子对其贡献之和,即为该点处的粒子数密度。
2.1 与观测数据的对比
为验证模拟结果中粒子分布情况,将模拟结果与Geotail 卫星观测结果进行对比。由于Geotail 卫星在10 月22-23 日处于本文设定的模拟区域之外(GSM 坐标x> 20Re),所以只能比较24-25 日期间卫星进入模拟区域的结果。IMF 长时间北向是在23 日,与Geotail 观测数据的比较无法获取IMF 北向期间的信息,但模拟结果与观测结果的对比依然有助于确定模拟结果的可信度。
如图3 所示,图3(a)为Geotail 卫星观测的低能粒子(Low Energy Particle)数密度,图3(b)为粒子模拟结果中Getotail 卫星所处位置的粒子数密度,图3(c)为Geotail 卫星在GSM 坐标系中的x坐标位置。
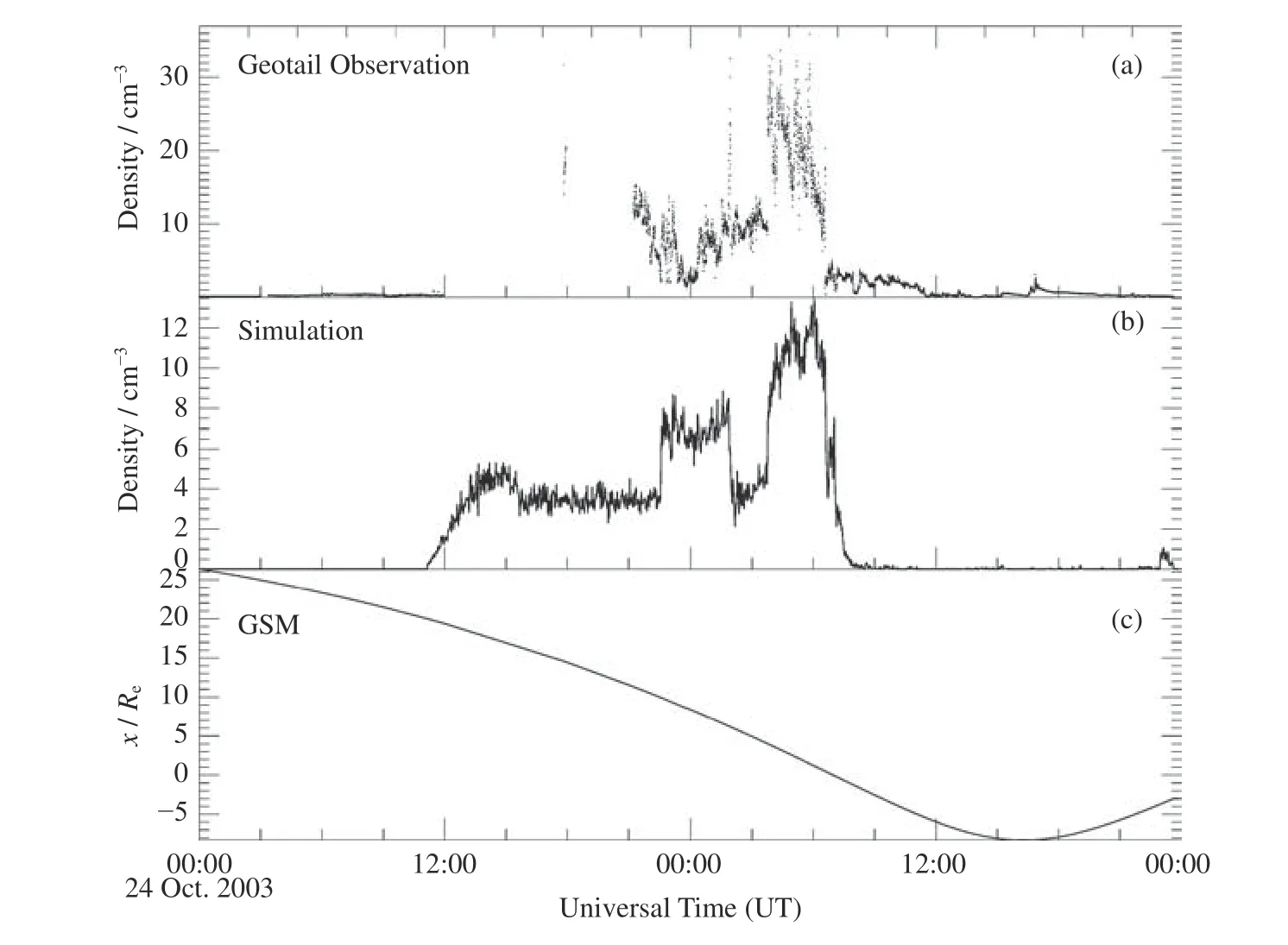
图3 Geotail 卫星观测粒子密度与模拟结果对比Fig.3 Comparison between the particle density observed by Geotail and that from our simulation
太阳风粒子从模拟区域的边界(x=20Re处)进入模拟区域,首先进入的是弓激波上游的太阳风区域,模拟结果中粒子密度比较稳定。太阳风进入磁鞘后,粒子密度有明显的增强和波动。最后在磁层内部,粒子密度相比磁鞘区域显著降低。观测数据的粒子密度比模拟结果要大数倍,这主要是因为本文的模拟粒子数量有限所致,另外,模拟中只计算了质子,未考虑其他粒子的影响。Geotail 的观测数据存在一些缺失,但是其变化趋势与模拟结果基本吻合,表明本文的模拟结果能够反映太阳风-磁层相互作用过程中粒子的分布情况。
2.2 太阳风粒子在磁层中的三维分布
在IMF 北向期间,太阳风粒子可以通过多种机制和途径进入内磁层和磁尾区域[18],由于IMF 北向时的太阳风进入近地磁尾并未经过显著的加热加速过程,所以与IMF 南向时相比,在磁尾中的等离子体片温度偏低,密度偏高,从而形成冷而密的等离子体片(Cold Dense Plasma Sheet,CDPS)[33]。在模拟时间t=66600 s,对应物理时间为2003 年10 月22 日18:30 UT 左右,此时是长时间IMF 北向的起始阶段,进入磁层的太阳风粒子密度分布如图4 所示(图中磁层顶位置是通过流线方法识别得到的[34],弓激波位置是利用磁流体速度突变为判定标准识别得到的)。此时进入磁层中的粒子数量较少,进入磁层的粒子主要分布在南北极尖区和环电流区域。在磁层顶附近,越靠近磁尾,越过磁层顶进入磁层的太阳风粒子越多,不过这些粒子主要分布在磁层顶内侧附近,很难深入磁层内部。
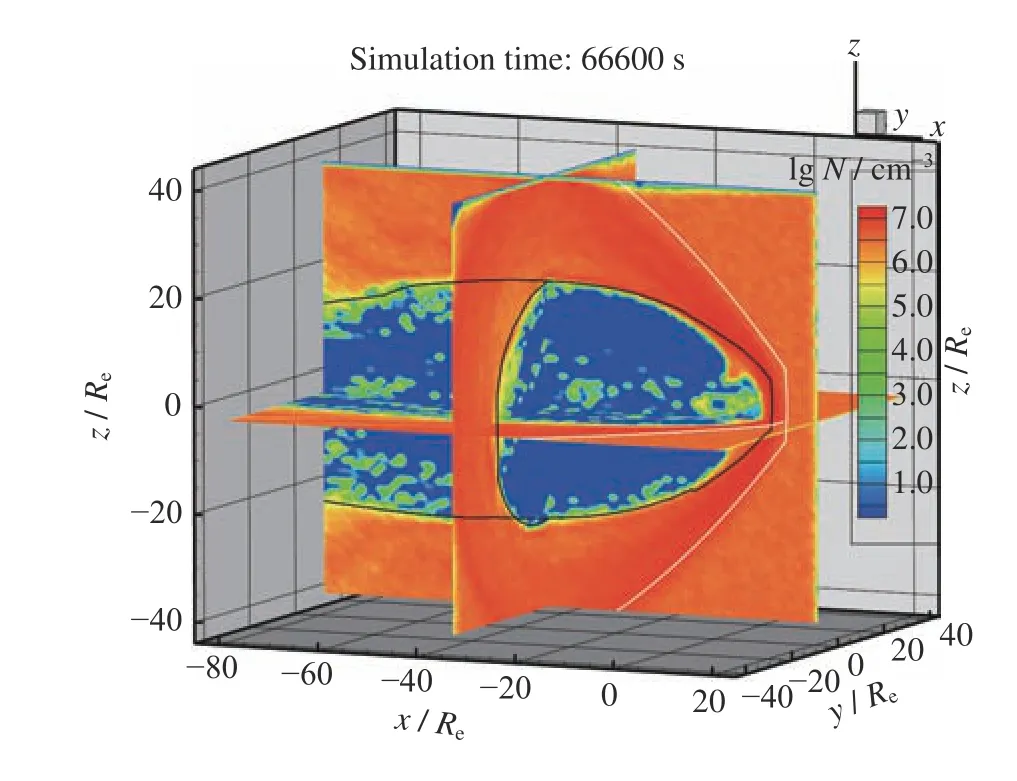
图4 太阳风粒子在磁层中的三维密度分布(黑色实线为磁层顶位置,白色实线为弓激波位置)Fig.4 Three dimensional density distribution of solar wind particles in magnetosphere (Black solid lines mark the location of magnetopause,and the white solid lines mark the location of bow shock)
再选取模拟时间为170000 s 的模拟结果,对应物理时间为2003 年10 月23 日23:13 UT 左右,此时IMF 长时间的北向过程已经快要结束,太阳风粒子在磁层中的三维密度分布如图5 所示。与IMF 北向起始阶段不同,此时已经有大量的太阳风粒子分布在磁层内部,南北极尖区和环电流区域的粒子数显著增多,在磁尾区域,出现了粒子聚集区。为了更清晰分析磁层内部粒子密度分布,取xy,xz,yz三个截面进行分析。
图6 为图5 所示的赤道截面,由于考虑了磁倾角,所以地球赤道面与GSM 坐标的xy平面并不重合,为了便于观察近地磁层中的粒子分布,选取的截面接近赤道面。在晨昏两侧的磁层顶内,均有太阳风粒子的注入。等离子体片晨昏两翼中低能粒子密度的增加由磁鞘粒子注入引起[35,36],粒子可以穿越侧翼的磁层顶进入,也可以通过极尖区进入磁层。Sorathia等[37]认为通过侧翼磁层顶的KH 涡旋进入磁层的粒子在晨昏两侧的分布是对称的,而通过极尖区进入磁层的粒子表现出晨昏不对称性,进入晨侧等离子体片的粒子要多于昏侧。图6 中磁尾等离子体片靠近磁层顶位置的晨昏两翼存在晨昏不对称,晨侧粒子密度要大于昏侧,这与Wing等[36]的统计结果相符。近地空间的环电流区域捕获了大量的太阳风粒子,在地球赤道面形成完整的环状分布。环电流区域的粒子分布也表现出晨昏不对称性,晨侧粒子分布更宽,这可能是由于晨向电场与向阳面磁层内离子的西向漂移共同作用产生的[37],Yao等[38]统计结果表明晨侧磁层顶附近的动理学阿尔芬波能量要高于昏侧,这也可以导致晨侧穿越磁层顶进入磁层的粒子比昏侧多。
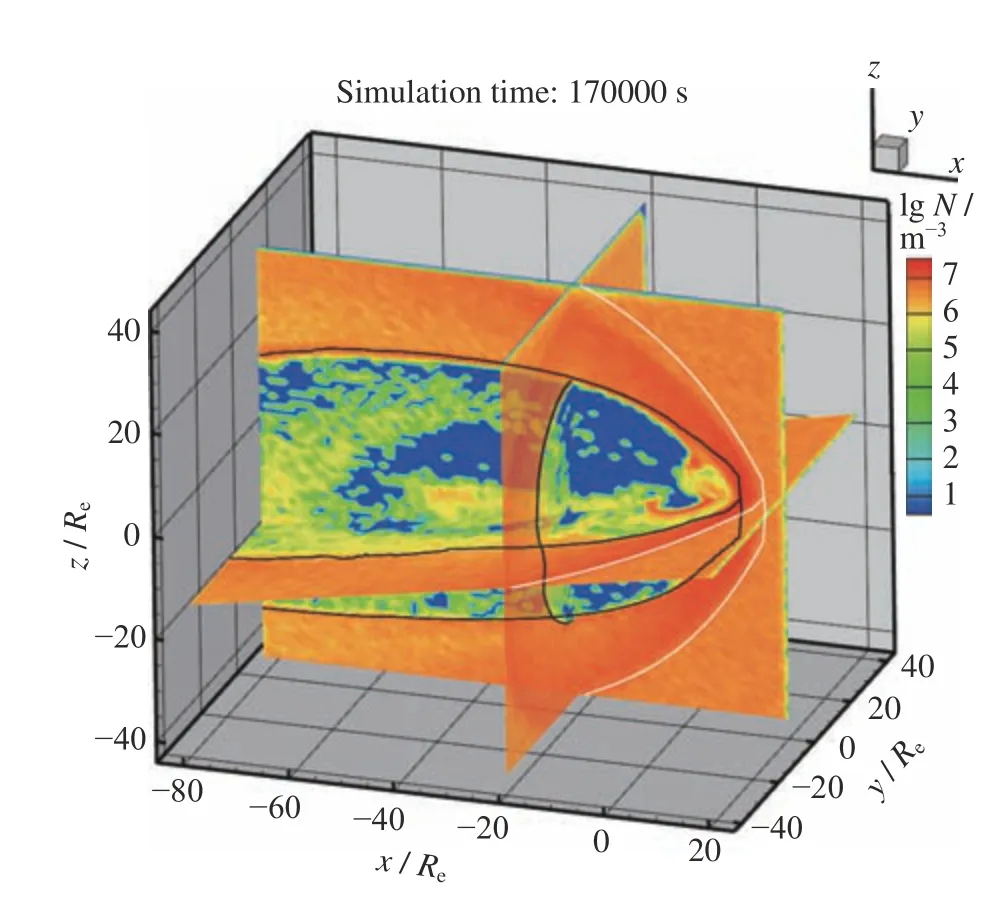
图5 太阳风粒子在磁层中的三维密度分布Fig.5 Three dimensional density distribution of solar wind particles in magnetosphere
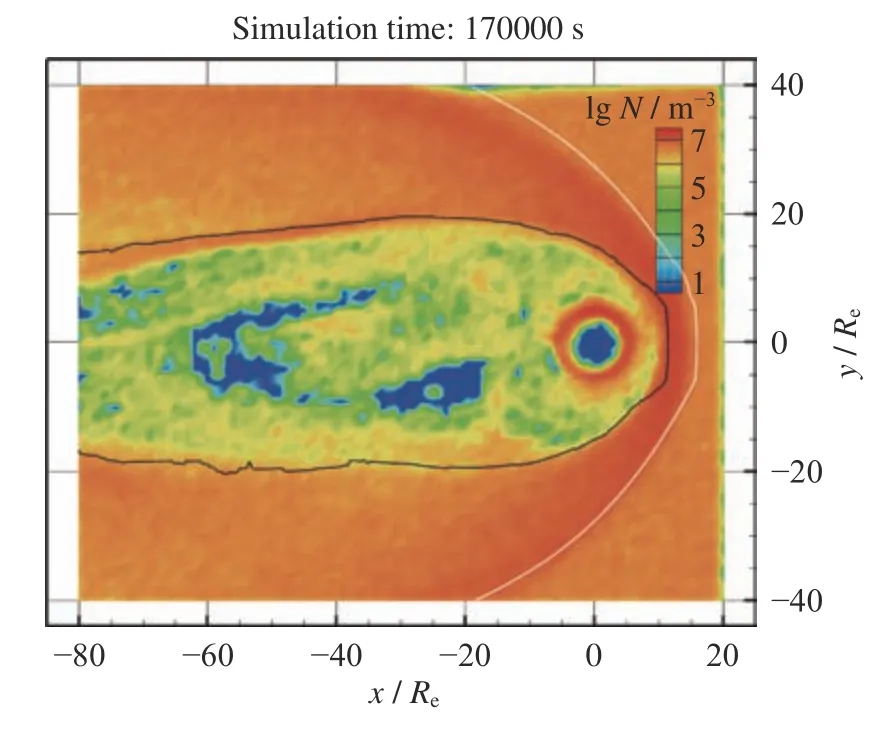
图6 太阳风粒子在xy 平面的密度分布Fig.6 Density distribution of solar wind particles in xy plane
子午面(xz)中粒子密度分布如图7 所示,图7 中可以清晰分辨出弓激波和磁层顶的位置,尤其是北侧磁层顶边界清晰,说明从北侧磁层顶进入磁层的粒子极少。南侧磁层顶内侧有少量粒子分布,特别是在远磁尾区域,说明有少量粒子可以通过南侧磁层顶进入磁层,这种南北两侧磁层顶的差异可能是受地磁偶极倾角的影响。观察南北极尖区中的粒子密度,南半球的极尖区中粒子密度更高,说明太阳风粒子更容易进入南半球极尖区,这也与地磁偶极倾角有关[3]。

图7 太阳风粒子在xz 平面的密度分布Fig.7 Density distribution of solar wind particles in xz plane
在磁尾-15Re<z< 5Re,x> -50Re的区域,存在粒子聚集区,也就是长时间IMF 北向时,在磁尾形成的冷而密等离子体片。Bai等[33]统计CDPS 事件主要分布在x< -10Re的区域,Li等[39]认为大部分的CDPS 观测位于x> -30Re的近地区域,Terasawa等[40]认为北向IMF 时磁尾粒子密度增加发生在-50Re<x< -15Re,的区域,这与图7 中的分布范围基本符合。同时也注意到,在x≈ -75Re附近,存在另一个粒子密度较大的区域。
CDPS 事件的基本特征为粒子密度较大(>1 cm-3),10 月22 日IMF 北向持续3 h 后,Cluster 卫星观测到粒子密度达到1.5 cm-3,在这个水平维持了约30 h,DMSP 观测到此期间的粒子密度平均为 2~3 cm-3[41]。图7 中磁尾等离子体片区域密度较大处的lgN略大于6,也即粒子密度略大于 1 cm-3。虽然密度最大的区域满足CDPS 对密度的要求,但是与观测数据相比还是略小,这是因为模拟中的粒子数量较少所致,虽然采取了给粒子赋予权重的方法,但与实际观测相比,还存在粒子数量偏少的问题。
图8 所示为磁尾x=-20Re处yz平面内的粒子密度分布。磁尾南北尾瓣粒子分布极少,位于赤道附近的低纬边界层增厚,这与Sckopke等[42]的结果相一致。LLBL 区域的粒子密度也比较高,lgN可达到6~6.5 cm-3左右,也即粒子密度在 1~3 cm-3左右。Ding[3]计算得到IMF 北向期间LLBL 密约为3.2 cm-3,而观测结果一般在0.1~10 cm-3,均与本文的计算结果吻合。除了赤道附近的LLBL,还存在一个从左上(北-晨侧)到右下(南-昏侧)的粒子分布结构。Guo等[43]分析认为,在IMF 北向时,磁尾横断面会出现显著的由北-晨侧和南-昏侧指向磁层内部的粒子流,可以用来解释IMF 北向时磁鞘粒子对等离子体片更高的注入效率。
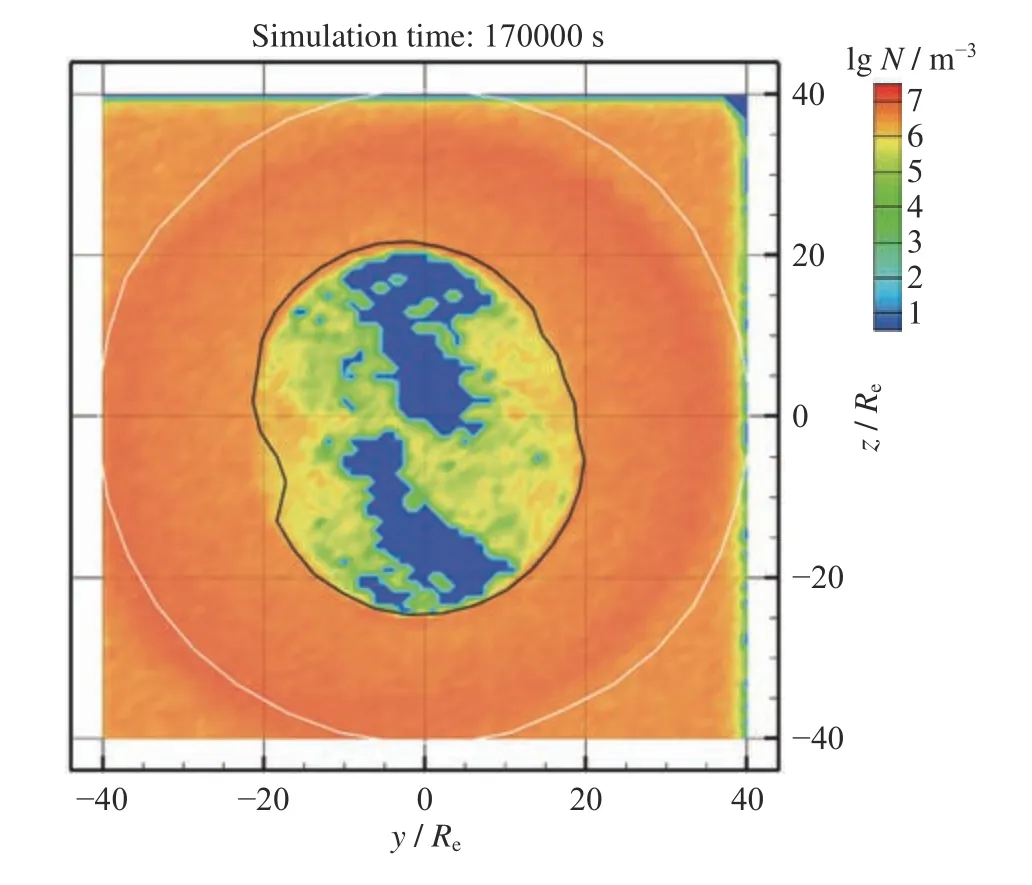
图8 太阳风粒子在 x=-20 Re 处的yz 平面的密度分布Fig.8 Density distribution of solar wind particles in yz plane at x=-20 Re
2.3 磁尾粒子数量的时间演化
太阳风粒子进入磁层的过程并不是一个稳态的过程,粒子进入磁层的速率也不是一成不变的。在长时间的IMF 北向期间,磁尾电流片中的粒子总数也应该随时间有所变化,为了研究磁尾粒子数量的变化情况,简单划定一个长方体形状的区域(-40Re<x<-10Re,-15Re<y< 15Re,-10Re<z< 10Re),分析其中粒子平均密度和最大密度值随时间的演化特征。如图9 所示,图9(a)为磁尾划定区域内的粒子平均密度,图9(b)为区域内粒子密度最大值。起始时间为IMF长时间北向的开始(t=66600 s,22 日18:30 UT),结束时间为IMF长时间北向结束(t=181800 s,24 日02:30 UT)的时刻,竖虚线为前文分析三维密度分布所使用的时刻(t=170000 s)。
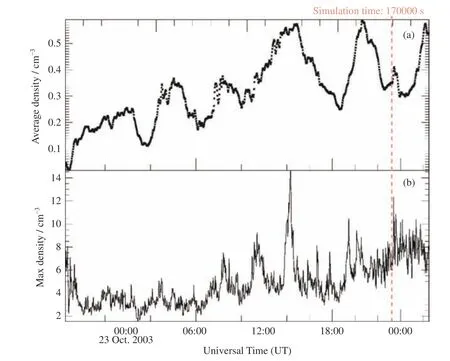
图9 磁尾选定区域(-40 Re < x < -10 Re,-15 Re < y < 15 Re,-10 Re < z < 10 Re )内的粒子平均密度和密度最大值在IMF 北向期间随时间的变化Fig.9 Variation of total particle average density and particle max density maximum during northward IMF in the selected magnetotail region (-40 Re < x < -10 Re,-15 Re < y < 15 Re,-10 Re < z < 10 Re)
粒子平均密度变化曲线中,可以看到在大部分时间都存在一个幅度较小的准周期性变化,周期大约为20 min,在平均密度曲线没有剧烈变化时比较明显。最大密度值曲线变化趋势与平均密度曲线相仿,不过由于密度最大值存在较大的偶然性,所以曲线抖动比较明显。Sorathia等[37]分析了约1 h 的粒子注入速率,发现晨昏侧翼的粒子注入存在约几分钟的短时变化,极尖区注入的粒子存在约8 min 的准周期变化。粒子平均密度存在的约20 min 的短时变化特征,可能跟磁层顶晨昏两翼以及南北极尖区等的注入机制存在短周期变化有关,是多种机制共同作用的结果。
从两个曲线都可以看出,在IMF 长时间北向期间,磁尾区域粒子数量存在持续增加的趋势,在这个趋势上,平均密度曲线还存在一个幅度较大的准周期变化,周期约为 5~6 h。这表明,在IMF 长时间北向期间,磁尾等离子体片中的粒子并不是处于稳定状态的,而是可能存在一种从聚集到释放,然后再聚集的循环过程。
3 结论
以ACE 卫星实时观测数据驱动的BATS-R-US全球MHD 模拟作为背景场,选取2003 年10 月22-24 日的长时间IMF 北向事件,使用试验粒子法对太阳风粒子向磁层输运的过程进行模拟研究,分析讨论北向IMF 时太阳风粒子注入磁层的过程以及粒子在磁层中的分布和时间演化特征。
使用全洛伦兹方程对粒子轨道进行求解,并选用变时间步长的方法,根据粒子的回旋周期,自动调整时间步长。通过对比分析几种不同的时间步长取值对粒子运动轨迹的影响,综合考虑求解精度和运算量,最终选用时间步长为回旋周期的1/100。将一千万个粒子从磁层外太阳风上游随机选择位置入射进入模拟区域,跑出模拟区域的粒子重新回到入射位置,使得模拟区域内一直保持一千万粒子的规模。模型中粒子密度与Geotail 卫星观测数据具有一致的变化趋势,表明模拟结果可以反映太阳风-磁层相互作用中的粒子分布情况。
在IMF 长时间北向的初期,进入磁层的粒子数量较少,主要分布在环电流区域和南北极尖区。IMF 长时间持续北向后,不仅南北极尖区和环电流区域的粒子数量大量增加,在磁尾也聚集了大量的粒子。磁尾等离子体片粒子密度分布存在晨昏不对称,晨侧粒子密度高于昏侧;环电流区域的粒子分布也存在晨昏不对称,在晨侧粒子分布的范围更广。磁尾南北侧磁层顶边界清晰,南北尾瓣粒子密度极小,而低纬边界层区域粒子密度大,表明磁鞘中的太阳风粒子基本不会通过南北磁层顶进入磁层,低纬边界层是磁鞘粒子进入磁层的一个主要通道。
长时间的IMF 北向使得太阳风粒子进入磁层并积累在磁尾,形成了冷而密的等离子体片。磁尾等离子体片的粒子聚集区在x> -50Re,-15Re<z< 5Re的区域,粒子密度略大于1 cm-3,达到了CDPS 事件的标准。在磁尾存在从北-晨侧向南-昏侧的粒子密度分布结构,这与IMF 北向时,磁鞘粒子向磁层的注入增强有关。
本文分析了磁尾一个指定区域内的粒子数随时间的演化特征。在IMF 长时间北向期间,磁尾粒子数量呈现出明显的增长趋势,并存在约20 min 的小幅度准周期变化和约 5~6 h 的较大幅度的准周期变化。小幅度的短时变化可能是由粒子注入机制存在短周期变化引起,较大幅度的长周期变化则表明磁尾等离子体片中的粒子并不是稳态的,而是应该存在一种从聚集到释放,然后再聚集的循环过程。
致谢ACE数据由ACE SWEPAM仪器团队和ACE 科学中心提供。模拟结果由位于戈达德太空飞行中心的CCMC(http://ccmc.gsfc.nasa.gov)提供。BATS-RUS 模型由密歇根大学空间环境建模中心(CSEM)Tamas Gombosi 博士等开发。Geotail 等离子体数据由Saito Y 通过日本宇宙科学研究所的数据档案和传输系统(DARTS)提供。

