运输机升阻特性仿真与风洞试验相关性方法
王定奇, 李密, 高翔, 李秋锋
(中国飞行试验研究院发动机所, 西安 710089)
军用运输机最重要的用途之一是将一定的载荷(包括人员、设备等)运抵至规定地点,有效载荷、航程是衡量大型运输机性能的重要指标。因此军用运输机在研发阶段以及交付使用前,需对有效载荷、航程等关键指标给出鉴定结论,对飞/发一体化设计水平和动力装置性能特性进行评估,而运输机平台性能的优劣与飞/发一体化设计水平高低的直观体现是能否准确获得飞机升阻极曲线。在飞机研制的设计阶段通常借助于比例模型风洞试验获得飞机系统和短舱通流模型的升阻极曲线[1-3],然而,短舱通流模型风洞试验中没有考虑到发动机状态变化引起的飞机升力、阻力及俯仰力矩的变化,对于飞机升阻极曲线带来误差。
当短舱为通流模型情况下,风洞天平中获取的风轴下的阻力相当于机体阻力;而短舱带动力情况下,风洞中天平所获取的力相当于额外推力,此时机体系统的阻力需要通过安装净推力和风洞天平力来确定。在带动力进排气气动特性的影响试验中,国外主要采用进排气模拟装置(turbine powered simulator, TPS)和引射喷管装置两种形式进行了研究[4-5]。TPS和真实发动机相比,除不能模拟高温喷流以及进排气流量比小于1.0外,其余特征与真实发动机非常接近,但针对本次试验条件,TPS尺寸较小,无法在与TPS配套的短舱外表面布置足够的静压测点。考虑到本项目的成本和试验周期,选取引射器短舱作为风洞动力模拟试验的发动机模拟器。
本文所研究的大涵道比涡扇发动机,短舱的轴向尺寸较短,进排气流动耦合程度较高,试验中无法单独将进气溢流阻力与排气干扰阻力进行计算,因此必须借助全三维仿真(computational fluid dynamics, CFD)方法和缩比模型试验确定各项力的组成。国外较早开展了针对带动力飞机的数值模拟研究[6-10],分析了发动机安装位置,发动机状态及飞行状态等对安装性能的影响,并开展了风洞试验和数值仿真相关性研究,形成了相关推阻力划分体系[11-12]。国内这方面起步较晚,谭兆光等[13]就动力效应做了初步探索,主要为了确定(Navier-Stokes equations, N-S)方程的可行性;但带动力与组合体之间的相互干扰,没有深入研究。李强等[14]利用CFM56发动机喷流试验结果对比,由于没有公开的数据对比,存在一定的误差。Zhang等[15]通过数值模拟,对民机中短舱通流模型和带动力模型的阻力特性进行了对比分析。高翔等[16]利用风洞试验数据对数值计算方法进行验证,总结了溢流阻力及排气干扰阻力的变化规律。
通过上述研究可以看出,目前主要针对通流模型或带动力模型的流场干扰问题开展了一定研究,而对于对带动力运输机升阻特性CFD与风洞试验相关性研究的较少。现针对带动力运输机CFD仿真,对不同马赫数、不同攻角和不同发动机状态进行计算分析,提取出各项阻力,并通过风洞试验进行对比,验证CFD方法获取飞机升阻特性正确性。随后以风扇压比FNPR=1.61时为基准,获取该发动机状态下不同攻角时,带动力运输机CFD计算结果的修正因子;将该修正因子运用到其他发动机状态,使各飞行状态及发动机状态下CFD计算得到升阻特性达到最优解,进一步验证带动力运输机升阻特性的相关性方法。
1 数值计算方法和网格生成
1.1 计算方法
对于黏性起主导作用的机翼扰流问题,其流场伴随着尾迹混合、流动分离机附面层的干扰等复杂流动特性[17-21]。本文研究采用有限体积法求解该方程,空间离散格式为二阶迎风Roe格式,时间推进格式为LU-SGS格式。综合考虑计算效率和计算精度,流场模拟采用加强型S-A湍流模型[22]。
1.2 模型及网格
试验采用的模型为M3飞机的1∶10动力半模模型,参数如下:参考面积为0.455 m2,平均气动弦长:0.341 5 m,机翼展长:1.444 m,翼展2.5 m,机翼面积1.2 m2,展弦比6.7。数值计算中需要对几何模型进行相应的简化:①删减试验件几何模型中的引气管路、测耙管路等附属结构,仅保气动影响的几何型面;②删减尾喷管进口至进气道出口中间的引射器几何构型;③忽略试验件表面缝隙、凸台等微小因素的影响。简化后的模型如图1所示。
动力系统的内外涵采用非结构四面体网格,涵道壁面第1层网格0.4 mm,增长率1.1,共11层;内外涵网格量为300万,发动机内外涵表面网格分布如图2所示。

图1 简化后的发动机模型Fig.1 Engine model after simplify

图2 发动机内涵表面网格分布Fig.2 Distribution of grid on surface of engine
根据该飞机的结构尺寸,半模计算区域选择长50 m、宽15 m和高15 m的长方体作为计算控制域,结构体形状及飞机模型在计算域中的位置如图3所示。对整机采用非结构化网格进行划分,靠近机翼/短舱/吊挂区域进行网格加密,远离机身区域计算网格逐渐稀疏,固壁面均采用7层网格进行加密,第1层网格高度为1 mm,增长率1.2,飞机半模网格量为550万,飞机表面流场分布如图4所示。

BODY为体图3 整体计算域Fig.3 Intergral computational domain

图4 飞机表面网格分布Fig.4 Distribution of grid on surface of plane
1.3 数据选取
试验中总温、总压测量耙的参数是以稳定状态点的直接测量参数作为输入条件的,但试验中的稳态数据采集,会因各种不确定的原因出现一些异常值,如瞬时或者间断性的测量系统故障或参数真实的波动等,从而无法得到发动机关键参数的真实值,必须剔除所谓的异常值。对于风洞中常规测力试验,数据采集测量时,待速压稳定后,等待2 s,测试系统采集1 s,每点采集1 000次,所以需对风洞验证试验的原始数据进行异常值剔除和数据平均等预处理。
根据阿诺德工程研究中心提出的改进的莱茵达准则判断异常值[23],其基本思想与莱因达法则相同,以C倍测量值样本均值的标准偏差作为置信区间,超过此区间的予以剔除。具体表达式为
(1)
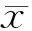
(2)
式(2)中:N为样本数;若N≥65,则C等于3,与莱茵达准则相同。将测试系统采集的稳态试验数据按照改进的莱因达准则进行剔点和算术平均,得到对应风洞试验点的参数平均值。以来流Ma=0.2、α=0°的工况下,不同发动机状态下各个截面参数,如表1所示。
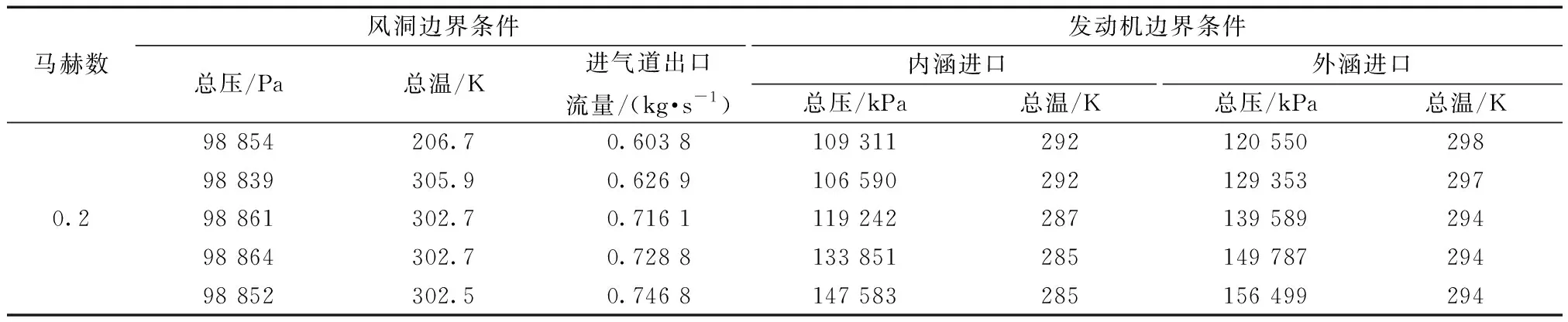
表1 计算边界条件设置Table 1 Boundary condition of calculation
2 涡扇发动机安装阻力计算
2.1 风洞试验中安装阻力计算步骤
风洞试验采用半模模型,受力如图5所示。
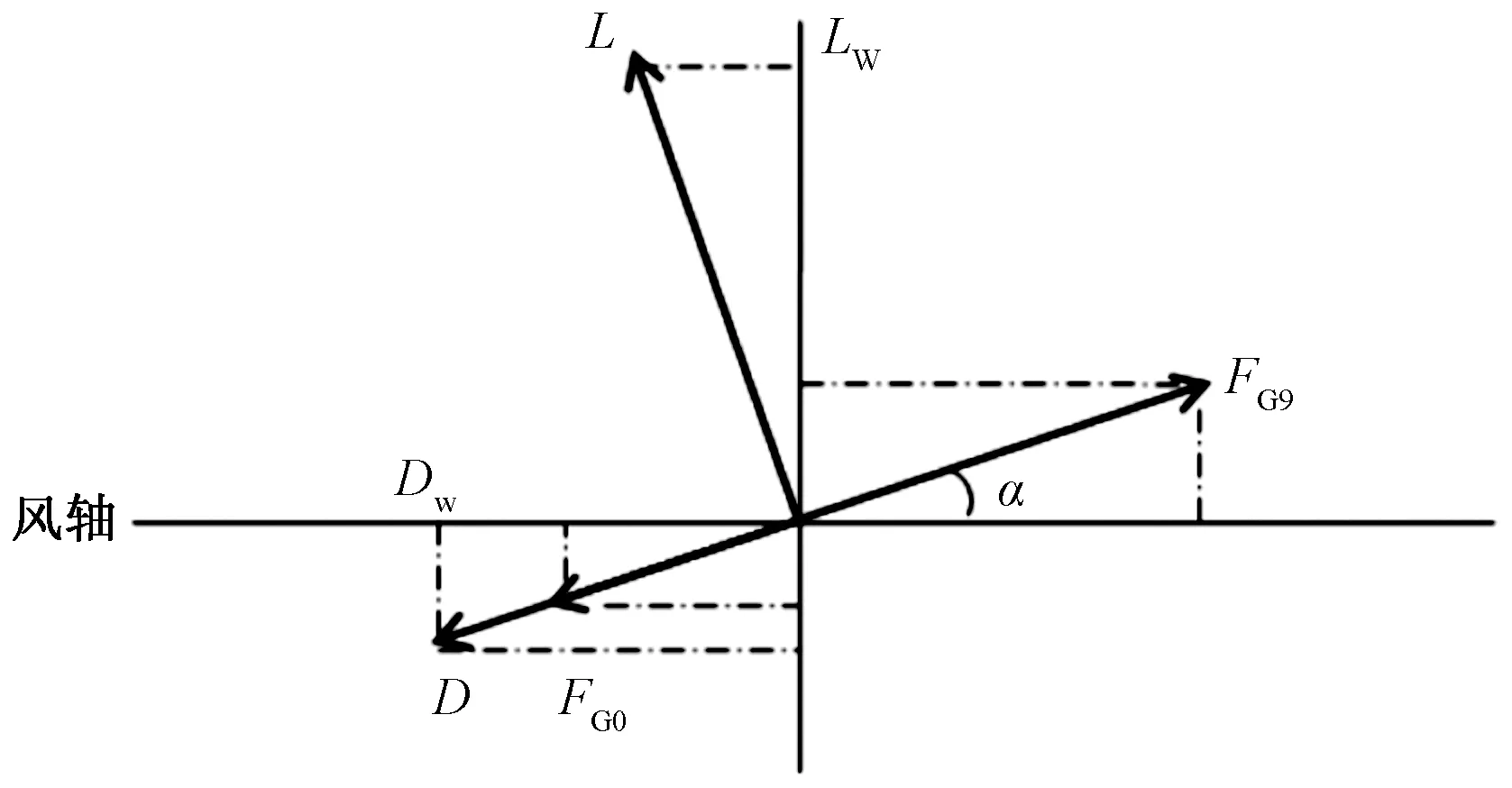
图5 飞机机体受力分析Fig.5 Force analysis of plane
整个试验中侧滑角为0,推力与机体参考轴线的夹角也为0。
LW+ΔFE-wind-L+FG9sinα=ΦL-wind
(3)
FG9cosα-FG0-ΔFE-wind-D-DW=ΦD-wind
(4)
式中:LW为风轴坐标系中的升力;ΦL-wind为风轴坐标系中天平测取的升力方向的力;FG0为阻力;DW为风轴坐标系下的阻力;ΦD-wind为风轴坐标系中天平测取的推力方向的力;ΔFE-wind-L为与动力装置状态变化相关的增量力在风轴升力方向上的分量;ΔFE-wind-D为与动力装置状态变化相关的增量力在风轴阻力方向上的分量;FG9为发动机推力。
当动力装置工作参考状态,在风轴坐标系下ΔFE-wind-L=0、ΔFE-wind-D=0,可得
(5)
(6)
当动力装置偏离工作参考状态时,在风轴坐标系下,可得
(7)
(8)
(9)
(10)
式中:上标0表示工作参考状态;上标X表示实际工作状态。
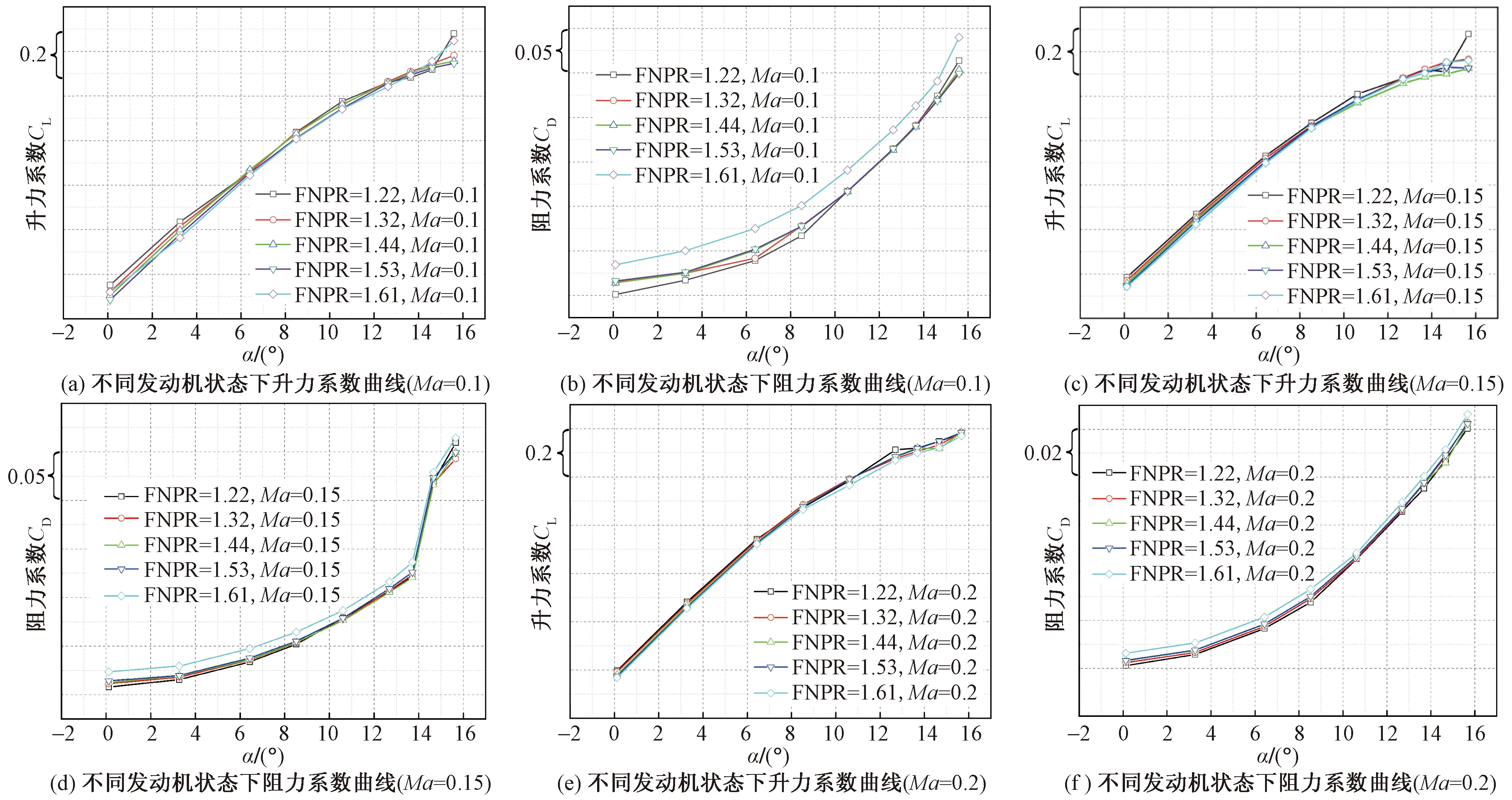
图6 半模飞机升阻特性曲线Fig.6 Curve of lift and drag for semi-plane
根据风洞试验数据,可得
(11)
(12)
式中:Ma为马赫数;FNPR为风扇压比;A0/A1为进气道捕获面积比;f为映射函数。
2.2 CFD仿真中安装阻力计算
外部阻力特性CFD仿真数据处理中的气动参数均可在算例结果中提取,包括内外涵总温、总压,环境温度、压力,内外涵尾喷管出口流量等,并利用数值积分获取半模飞机所有固壁面的压差阻力和摩擦阻力。风洞中获取的阻力和升力为附加前体力Φpre与半模飞机所有固壁面外部阻力Φa/c分别在升力和阻力方向的分量。全三维仿真计算结果中提取的升力和阻力应与上式保持一致,数据处理分为两部分。
(1)半模飞机所有固壁面外部阻力Φa/c计算。体轴坐标系下,在CFD计算结果中直接提取半模飞机各个部分固壁面所受外力在升力和阻力方向的分力,进行坐标转换,获得半模飞机所有固壁面外部阻力在风轴坐标系下升力和阻力方向的分力。
(2)附加前体力计算。即CFD获取的阻力为
D=FN-ΦD-wind=ΔFE+DW=Φpre+Φa/c
(13)
通过上述分析,可知风洞试验中,通过六分力天平获得飞机在风轴下的额外推力;前期校准箱试验获得的发动机喷管特性结合试验状态点可得到发动机的标准净推力。当选定发动机某一状态为参考状态时,可以通过标准净推力、附加前提力及天平力,计算出风轴下的机体阻力。
3 计算结果
3.1 半模飞机的升力-阻力特性
分别对比了9个不同攻角、5个发动机状态和3个马赫数条件下的飞机升阻特性曲线(图6),试验结果表明:①升力系数随着攻角的增大而变大,当攻角大于12°后,升力系数增幅逐渐减小,最大为1.2;阻力系数随着攻角的增大而变大,当攻角大于12°时,阻力系数迅速增大;主要是由于攻角大于12°后,气流通过机翼后分离较大,出现了一定的失速;②相同马赫数下,不同发动机工作状态下,升力系数随着攻角的变化曲线基本重合,而阻力系数随着发动机工作状态的增大而增大,表明发动机工作状态对升力系数影响较小,而阻力曲线影响较大。
3.2 流场分布

图7 飞机表面流场分布Fig.7 Flow field distributed on surface of plane
通过飞机表面压力云图(图7)可以看出,相同攻角和发动机状态下,随着来流马赫数的增大,在短舱前缘、机翼前缘压力升高,来流马赫数越大机翼上表面压力越低,飞机的升力随之增大。相同马赫数、相同发动机状态下,随着飞行攻角的增大,机翼下表面压力随之增大,且起飞构型下副翼和襟翼的压力增大程度明显,通过增大Ma和攻角α可以快速增大飞机的升力。
3.3 风洞试验值与修正后CFD计算值对比
由于本次试验模型时不仅存在飞机外流场的流动,还存在发动机喷管的内流与外流还有耦合情况,且整体计算模型尺寸较小,当发动机状态变化时,升力、阻力系数变化的绝对量有限,同时CFD仿真过程不可避免的与风洞中实际流动情况存在着差异,因此需对CFD计算结果进行修正。以FNPR=1.61时,试验获得的升力系数(CL)与阻力系数(CD)作为基准,在不同攻角下,获得CFD计算结果的修正因子,即
(14)
(15)
式中:下标FNPR表示风扇压比;下标EXP表示试验数据;下标CFD表示仿真计算数据。
根据以上修正因子,选取发动机状态点(FNPR=1.53)的CFD计算结果进行相关性验证,结果如图8所示。
通过对比可以看出:①CFD仿真与风洞试验获得的升力系数趋势一致,Ma=0.15与Ma=0.2情况下,升力系数最大误差仅为1.8%;Ma=0.1时,在大攻角条件下(α=15°)误差较大,达到7.1%,其余攻角条件下最大误差为2.5%;②CFD仿真与风洞试验获得的阻力系数趋势一致,Ma=0.15与Ma=0.2情况下,阻力系数与试验值基本贴合;Ma=0.1时,在小攻角(α<5°)曲线误差较大。
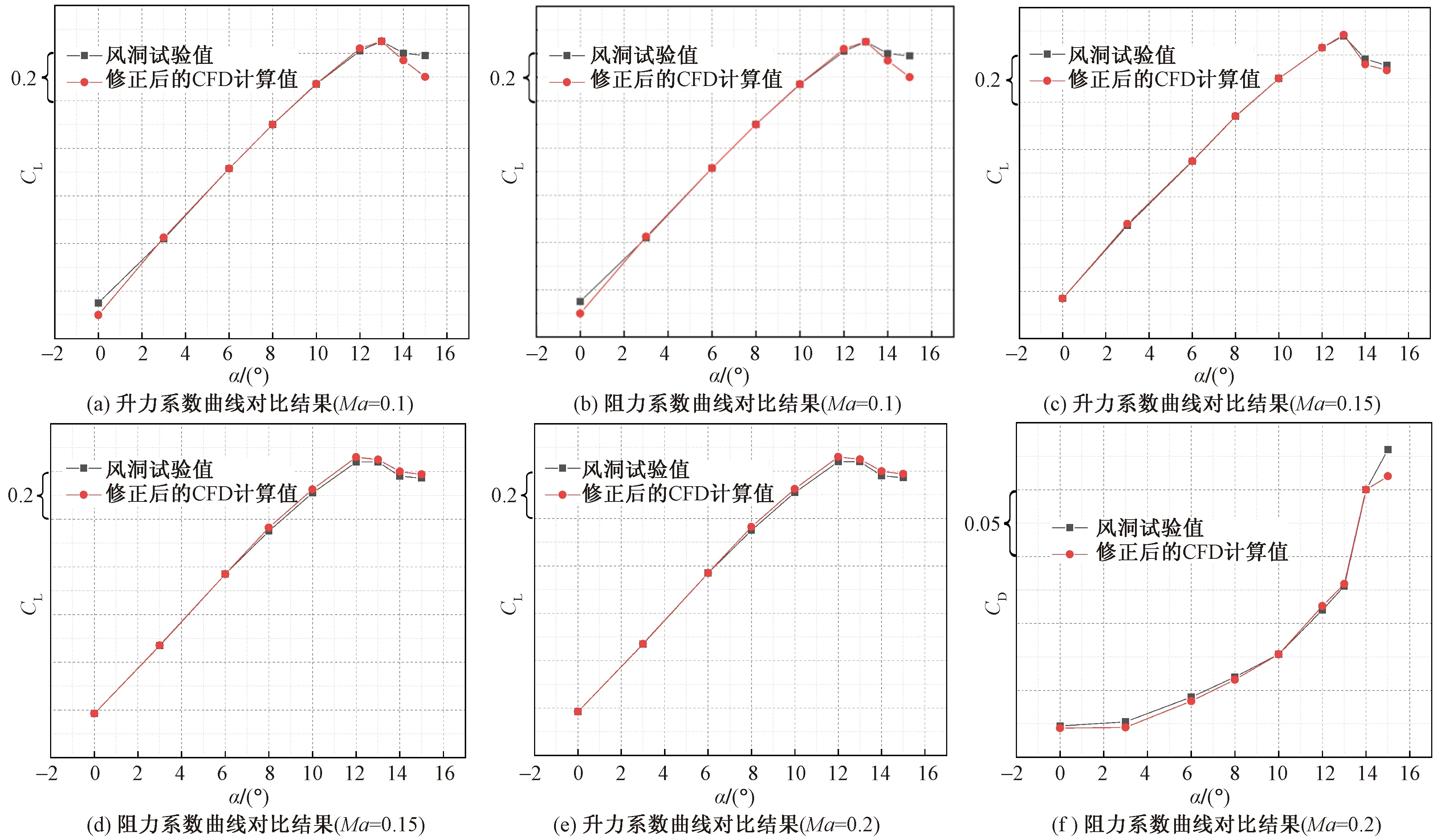
修正参考状态为FNPR=1.6图8 FNPR=1.53状态下升阻特性对比Fig.8 Comparison of lift and drag characteristic at FNPR=1.53
4 结论
以M3半模飞机配装某大涵道比涡扇发动机三维模型为研究对象,基于分区拼接网格对发动机内流和飞机外流场网格进行拼接,并设置与风洞试验相同的工况点进行流场数值仿真。分别对比了9个不同攻角、5种发动机状态和3个马赫数条件下的飞机升阻特性曲线进行对比,得到如下结论。
(1)升力系数随攻角增大而增大,当攻角大于12°后由于气流分离严重升力系数逐渐降低,最大升力系数为1.2;阻力系数随攻角增大而增大,攻角大于12°后,阻力系数迅速增大;
(2)相同Ma,随着发动机状态的增大飞机升力系数变化不明显,表明翼吊形式的发动机排气系统对飞机升力影响小;随着发动机状态增大阻力系数增大,表明发动机工作状态对阻力曲线影响较大;
(3)通过引入升阻修正系数,将CFD与风洞试验结果进行对比,升力系数相对比整体误差在4%以内;而阻力系数量级较小,与试验计算的趋势基本一致,表明本文的CFD计算结果可满足后续分析的基本要求。

