一类微分方程组特征值的研究
吴 平
(苏州市职业大学 数理部,江苏 苏州 215104)
基于文献[1]和文献[2]研究的问题及其内容,本研究提出一个新的微分方程组,研究其第n个特征值和第n+1个特征值的关系。该微分方程组中的方程阶比文献[1]和文献[2]相应的阶高,所以该问题是文献[1]和文献[2]中相应问题的推广。目前对微分方程特征值的研究较多[3-4],但对微分方程组特征值的研究较少。
1 问题的提出
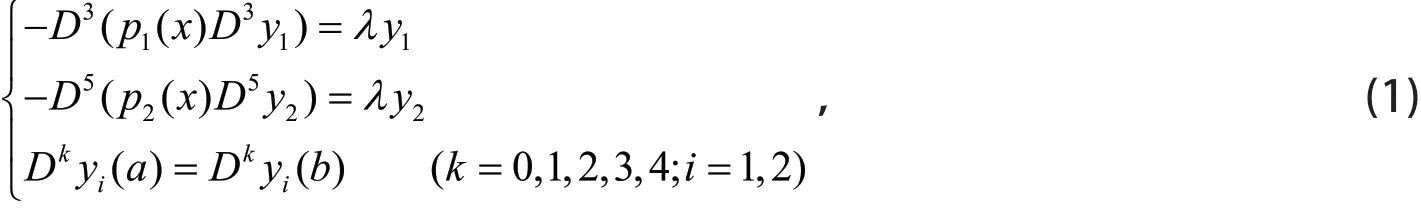

其中u1、u2为正常数。
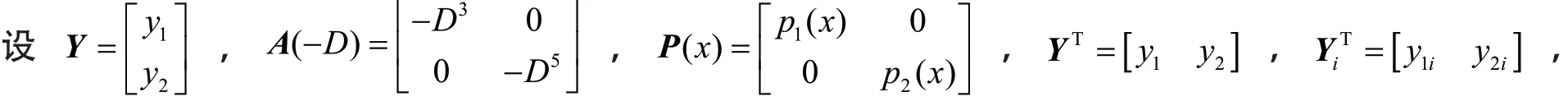

设方程组(3)的特征值为

对应的带权s(x)特征向量为Y1,Y2,...,Yn,...,且正交规范,即满足
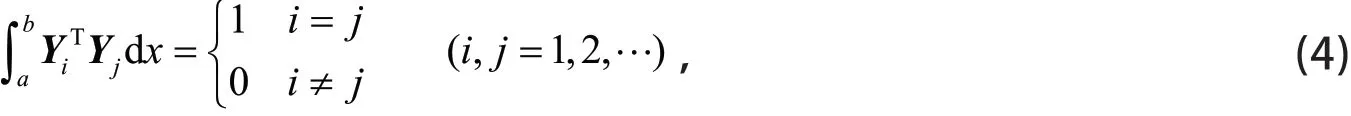
由分部积分得

由式(2)和式(5)得
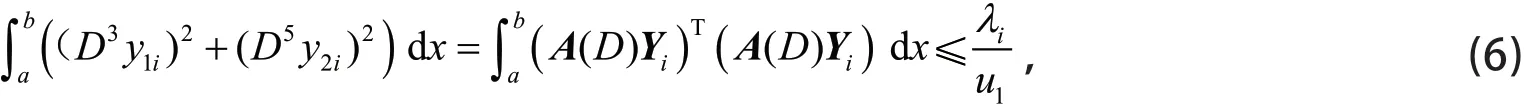
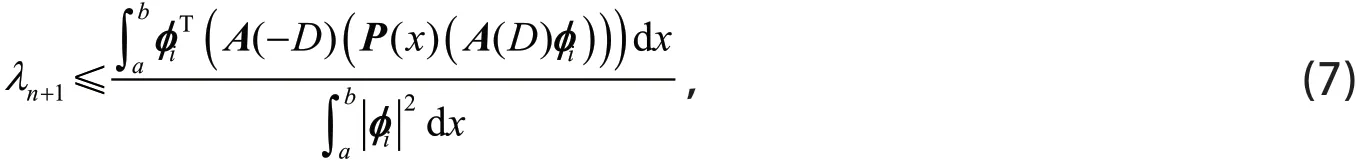
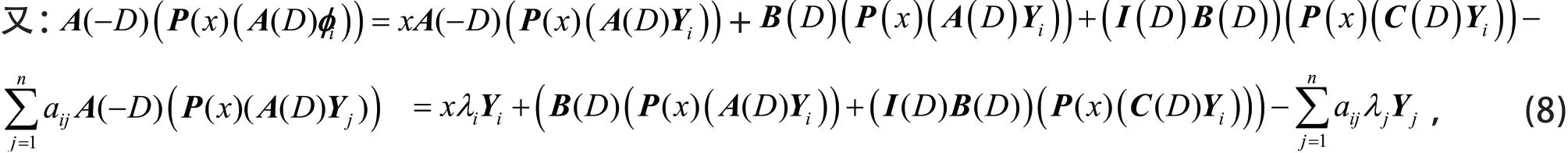
因φi与Yj正交,及,由式(8)得
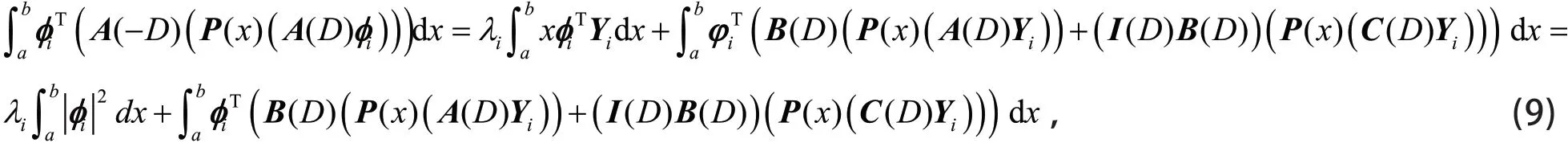

由式(7)和式(10)得

用nλ代替式(11)中的iλ,有

2 引理
为了证明问题(1)的第n个特征值和第n+1个特征值的关系,必须先证明下面的引理,在证明过程中参考了文献[5]和文献[6]中的引理及其证明过程。
引理1 设Yi是方程组(3)对应特征值nλ的特征向量,则
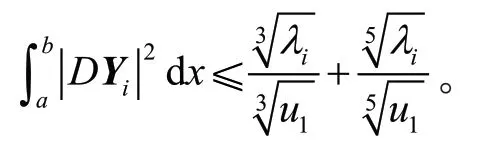
证明 由分部积分、Schwartz不等式、式(6),得
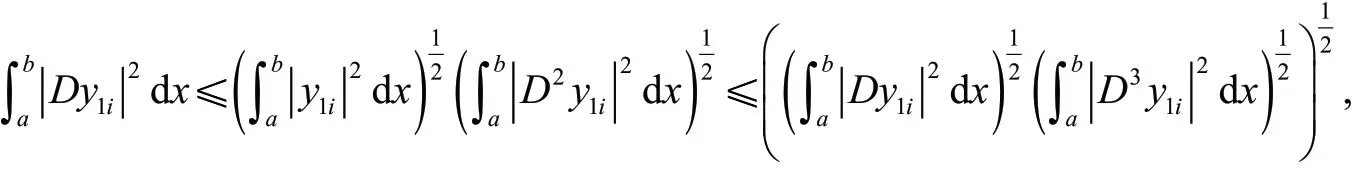
由式(6)化简得

同理,可得

由式(13)和式(14),得
即得引理1。
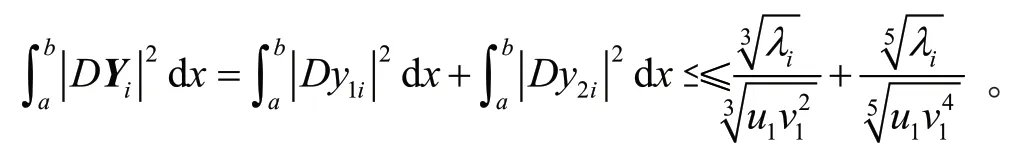
引理2 设λ1,λ2,...,λn是方程组(3)的n个特征值,则
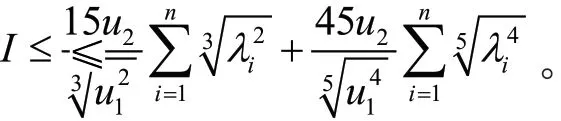
证明 由分部积分和iφ的定义得

由式(15),得

由式(2)、式(6)、式(13)、分部积分和Schwartz不等式得
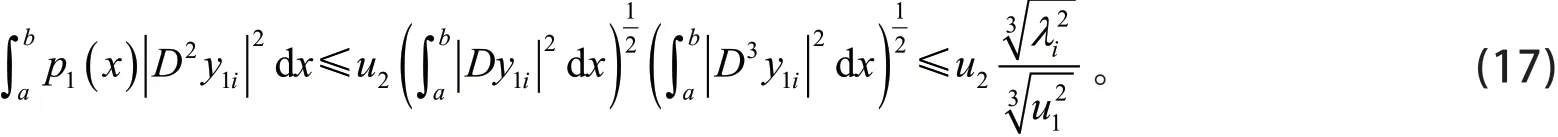
同理,得

由式(16)-式(20)得
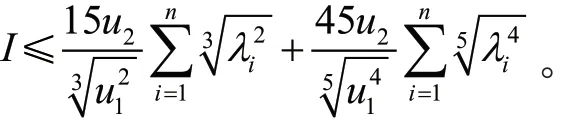
引理3 对于φi和λi(i= 1,2,...,n),则
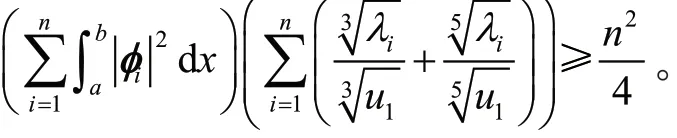
证明 利用iφ的定义得

利用分部积分有

利用式(22)有
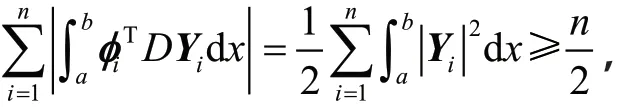
则根据Schwartz不等式和引理1,得

引理3得证。
3 结论
对问题(1)的第n个特征值和第n+1个特征值的关系,在证明过程中参考了文献[5]和文献[6]中的定理及其证明过程。
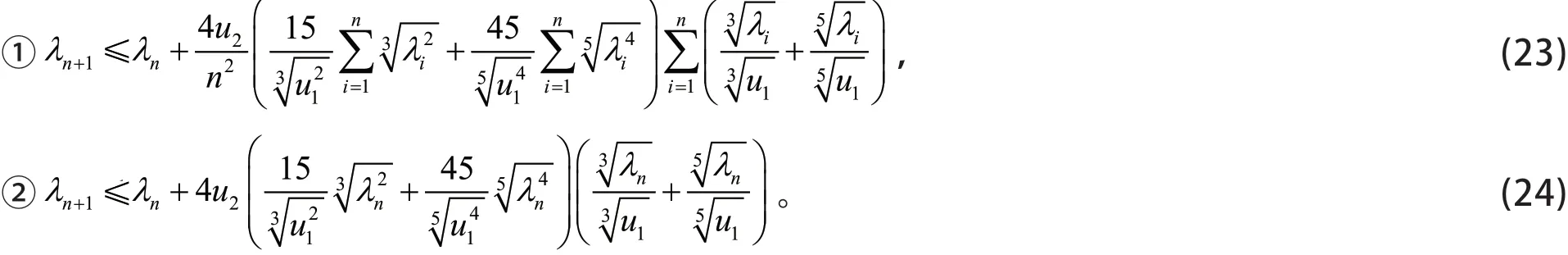
证明 根据引理3,有

再由式(12)和引理2,可得到定理1的式(23),并在式(23)中用λn代替λi,可得到式(24)。
定理2 对于n≤≥1,则

证明 取参数σ>λn,由式(11)得

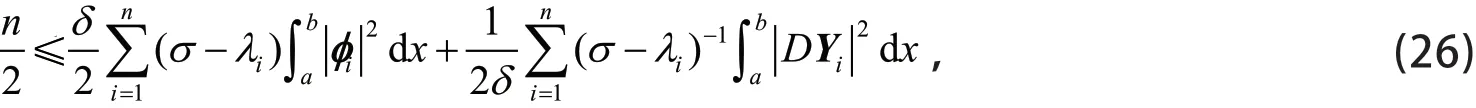
其中δ>0为待定常数。
使式(28)右端达到最小值,将式(29)代入式(28)有

由引理2、式(21)和式(30)式,得
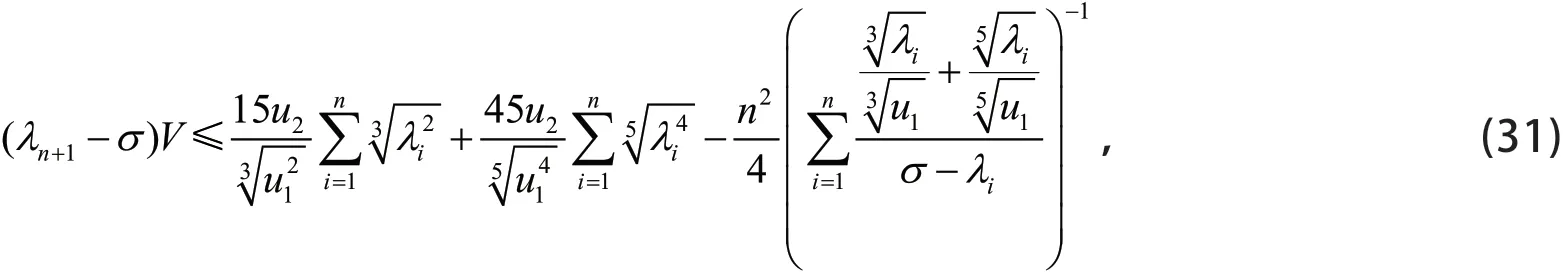
其中σ>λn,取σ使式(31)右端等于零,即


易知f(σ)是在(λn,+∞)内单调减少的连续函数,其值域为(0 ,+∞),因此,存在唯一的σ使式(32)成立。从式(31)知σ≤≥λn+1,用λn+1来替代等式中σ,即得定理2。
4 总结
方程的特征值问题是数学学科研究的一个重要领域,它涉及的内容复杂而广泛。研究一类微分方程组特征值的关系,并获得第n个特征值和第n+1个特征值的关系,即定理1和定理2,其结果在物理学和力学等领域有着广泛的应用。

