压轴主力：二次函数

文／吴琨

纵观每年各地中考试卷，二次函数一直是压轴题的主力军。那么，为什么二次函数在压轴题中占比很大呢？中考压轴题一般考查大家综合运用的能力，而二次函数具有知识点多、覆盖面广、条件隐蔽、关系复杂、思路难觅、解法灵活等特点。下面以2022年江苏省盐城市中考压轴题为例加以说明。

【发现问题】小明在练习簿的横线上取点O为圆心，相邻横线的间距为半径画圆，然后半径依次增加一个间距画同心圆，描出了同心圆与横线的一些交点，如图1所示，他发现这些点的位置有一定的规律。

图1

【提出问题】小明通过观察，提出猜想：按此步骤继续画圆描点，所描的点都在某二次函数图像上。

【分析问题】小明利用已学知识和经验，以圆心O为原点，过点O的横线所在直线为x轴，过点O且垂直于横线的直线为y轴，相邻横线的间距为一个单位长度，建立平面直角坐标系，如图2所示。当所描的点在半径为5的同心圆上时，其坐标为 。

图2

【解决问题】请帮助小明验证他的猜想是否成立。

【深度思考】小明继续思考：设点P（0，m），m为正整数，以OP为直径画⊙M，是否存在所描的点在⊙M上。若存在，求m的值；若不存在，说明理由。

【解析】

【分析问题】根据题意，可知所描的点在半径为5的同心圆上时，其纵坐标y=5-1=4。

所以点坐标为（-3，4）或（3，4）。

【解决问题】小明的猜想成立。

解法1：设半径为n的圆与直线y=n-1的交点为P（x，n-1）。

因为OP=n，

所以x2+（n-1）2=n2，即x2=2n-1。

所以点P在抛物线上。小明的猜想成立。

解法2：设半径为n的圆与直线y=n-1交点为P（x，n-1）。

因为OP=n，

所以x2+（n-1）2=n2，

所以点P在抛物线上。小明的猜想成立。

解法3：根据图中点的位置，猜想抛物线的对称轴是y轴，所以设抛物线的表达式为y=ax2+c。

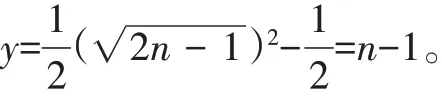
所 以P（2n-1，n-1）在 抛 物线上。

同理，P（-2n-1，n-1）也在抛物线上。

所以点P在抛物线上。小明的猜想成立。

【深度思考】

存在所描的点在⊙M上。理由：

又因为m、n都是正整数，

所以n-1=1。

所以m=1+2+1=4。

所以存在所描的点在⊙M上，m的值是4。

【点评】本题考查了勾股定理、二次函数图像上点的坐标特征以及与圆有关的位置关系。解题的关键是：【分析问题】利用勾股定理，求出该点的横坐标；【解决问题】根据点的横、纵坐标的关系，找出点在二次函数的图像上；【深度思考】利用勾股定理，用含n的代数式表示出m的值。

任何一个数学问题的解决都离不开转换思想。初中数学中的转换思想主要包括由未知转向已知，由复杂转向简单。而作为中考压轴题，其更注重不同知识之间的联系与转换。一道中考压轴题一般是融多种知识点于一体的综合性问题，转换思路在其中的运用显得更为重要。

同时，我们在做压轴题时，如果解不出来，无从下手，首先要消除恐惧感，将整道题目的解题思路转化为相应的得分点。中考数学压轴题一般会设置两至三个小题，难易程度是第1小题较易，大部分同学都能拿到分数；第2小题中等，起到承上启下的作用；第3小题偏难，不过也是建立在1、2两小题的基础之上。因此，我们在解答时要确保第1小题的分数，力争第2小题的分数，竭尽全力拿到第3小题的分数，这样就能大大提高获得中考数学高分的可能性。对于数学中考压轴题，我们应最大限度地发挥出自己的水平，勇攀高“分”。