故障共享单车的回收修理策略研究
毛 敏,鲍震天,唐优华+,秦 浩,艾明慧
(1.西南交通大学 交通运输与物流学院,四川 成都 611756; 2.综合交通大数据应用技术国家工程实验室,四川 成都 611756; 3.美团点评集团,北京 100080)
0 引言
共享单车作为一种新兴的业态,发展非常迅猛。2015年开始,共享单车不仅进入重点城市,还渗透到许多二三线城市,甚至出现在了伦敦、硅谷、东京、维也纳等国际都市。共享单车方便了出行需求,能够节约资源,保护环境。但由于管理、服务、经营等方面不到位,共享单车企业面临恶意损坏、缺乏监管和后续维护等问题,加之激烈的竞争,促使大批单车企业倒闭。进入河北保定、廊坊、北戴河等城市的3VBike,仅4个月宣布倒闭;位于福建莆田的卡拉单车仅上线运营19天(1)http://www.inewsweek.cn/viewpoint/2018-12-18/4625.shtml。。据《中国经济周刊》记者的调查,最高峰时,北京街头共享单车数量达235万辆,现在已不足191万辆;成都主城区的单车总量已经由180万辆减少到75万辆。运营车辆减少的同时却让废旧单车的回收问题日渐突出,部分企业报废车辆的费用甚至高于新车采购费,以致上海浦东、合肥庐阳等地都出现了“单车坟场”(2)http://www.ceweekly.cn/2019/0430/256209.shtml。。共享单车企业纷纷开始重视故障和废旧单车的回收,美团单车(原摩拜单车)通过将故障单车运到自营的维修厂进行维修,提高共享单车的有效利用率。当前,共享单车企业早期靠资本投放车辆的粗放式经营方式已经过时,如何增加用户黏度提升市场份额,降低运营成本成为目前共享单车企业运营的关键。故障共享单车的回收与维护修理会直接影响用户的出行体验,也有相应的运营成本。而合理的故障单车回收修理策略,可以在保证一定服务水平前提下有效降低运营成本。
产品回收是逆向物流中一个具体的例子,它需要从消费者到生产者的特定步骤,如收集、选择、处置或再加工、再分配和再利用[1]。NARDI等[2]通过案例研究,提出一种方法来检视及监察逆向物流产业运营及策略决策对经济、社会及环境的影响。废旧产品回收再制造的努力成本[3]、政府率规制[4]和企业社会责任都会影响企业对故障和老旧产品的回收力度[5-6]。不同行业的回收系统存在较大差异,电子行业中生产商自建回收系统收益最大[7],而在零售商品的回收中,零售商更有优势地位[8]。产品回收中不同的主导者会显著影响供应链的总收益和稳定性[9]。此外,回收平台能有效降低回收和处理成本,如惠普、伊莱克斯、索尼和布劳恩等制造商通过共同组建欧洲回收平台,在其运营的国家将制造商的回收和处理成本削减了35%[10]。产品召回与产品回收不同,例如公司生产资质、产品可靠性[11],出售产品的种类[12]和触发召回事件的信息来源[13]等许多因素都会影响召回决策,公司不仅要承担额外的物流成本,还要遭受声誉受损影响,导致供应中断风险[14],也会对消费者产生不良影响[15]。
物流网络的成本控制和优化历来受到重视。HALL[16]定义了3种不同类型的货物运输合并,包括库存、车辆和终端合并。在多对多网络中使用合并终端(相当于枢纽)的一个重要原因是成本降低,多位学者进行了相关研究。DAGANZ[17]研究了直接从始发地到目的地的运输与通过枢纽的运输之间的成本均衡;BLUMENFELD等[18]研究了通用汽车(General Motors)零配件配送的最佳装运策略,目的是降低包括运输和库存成本在内的总物流成本;DAGANZO[19]还研究了多对多网络结构,以确定枢纽数量和服务频率;CAMPBELL[20]分析了在多对多物流网络中,通过整合枢纽安排货运路线的3种方案;DAGANZO[21]在著作中描述了如何规划和设计有效的物流系统,针对有无转运系统的运输网络进行了讨论。以上学者的研究专注于获得使所有相关成本之和最小的最优策略。HARKS等[22]提出一种物流网络运输优化数学模型,包括通过关税结构和循环交付模式等实现物流网络的时空整合效应;BAZAN等[23]在一篇关于逆向物流库存模型的综述文章中,重点对考虑经济订单/生产数量和联合经济批量的文献进行了详细分析;NAGY等[24]发现当载具的装运量有限时,同时开展送货和取货作业会显著增加物流成本;周向红等[25]以回收网络系统利润最大和社会效益最大为目标,建立了多周期多目标废旧品回收网络模型。
近年来共享经济逐渐成为新的研究热点。LOWITT[26]详细阐述了共享经济成功的内在逻辑和未来的潜在机会,国外许多学者关注共享平台对行业和社会的影响,Airbnb的出现降低了酒店房费使消费者获利[27],同样Uber也极大地改变了城市交通政策的制定[28]和出租车市场的运行[29]。在共享单车领域,学者们利用包括K-means算法[30]、混合禁忌搜索算法[31]、自适应禁忌搜索算法[31]、混合遗传算法[33]等方法对故障单车的回收调度模型进行了研究。也有学者在一种单车故障预测模型基础上,为美团单车公司提出了一种基于散射搜索法的故障单车收集路径算法[34]。作为带有一定公共属性的服务,对共享单车的治理,需要政府规划引导[35],用户积极参与[36],共享单车企业也应该考虑承担企业责任[37],形成三方共同治理的局面。
目前对产品回收和召回的研究主要集中在工业产品和大众消费品,针对共享产品回收的文献很少,而共享产品不同于一般的工业产品和大众消费品,有独特的产品特征。另外,与产品回收目的不同,共享产品的回收是对共享产品回收后进行修理,再投入使用;与产品召回原因也不同,不会对企业产生负面影响,有利于提高企业的服务水平。近年来,共享产品的回收修理随着共享经济的发展正逐步受到关注。共享单车回收与维护修理的研究,目前主要集中在具体的回收模型和算法上,未从回收与修理的总运营成本改善角度进行研究。基于此,本文首先从单运营片区回收系统视角,通过对比满载情况下直运、转运和混合回收策略的总运营成本,给出了共享单车企业对故障单车的回收策略选择条件;然后在最优装运量下,分析了3种回收策略的选择条件;最后,针对全运营网络,在一定的运营能力下,以总运营成本最低为目标,给出了共享单车企业对装运方式和回收策略最优组合的选择。本文的研究可以为共享单车企业的故障单车回收修理业务提供决策依据。
1 基本问题
1.1 问题描述
目前,共享单车企业主要将城市划分为多个运营片区,自建有一个维修厂,负责故障单车的处理。从故障单车的搜集、集中、送厂修理到最后的再投放,均由共享单车企业完成。工作人员根据用户上报或在日常运作中发现的故障车辆,使用专门的卡车进行收集。根据维修厂的运行情况,部分故障单车被直接送往维修厂,部分故障单车因维修厂维修能力有限被运往暂存点,后面根据维修的排程,再次从暂存点运输到维修厂。最后,根据各运营片区情况,将完成修复的单车再次投入市场。共享单车回收维修流程如图1所示。
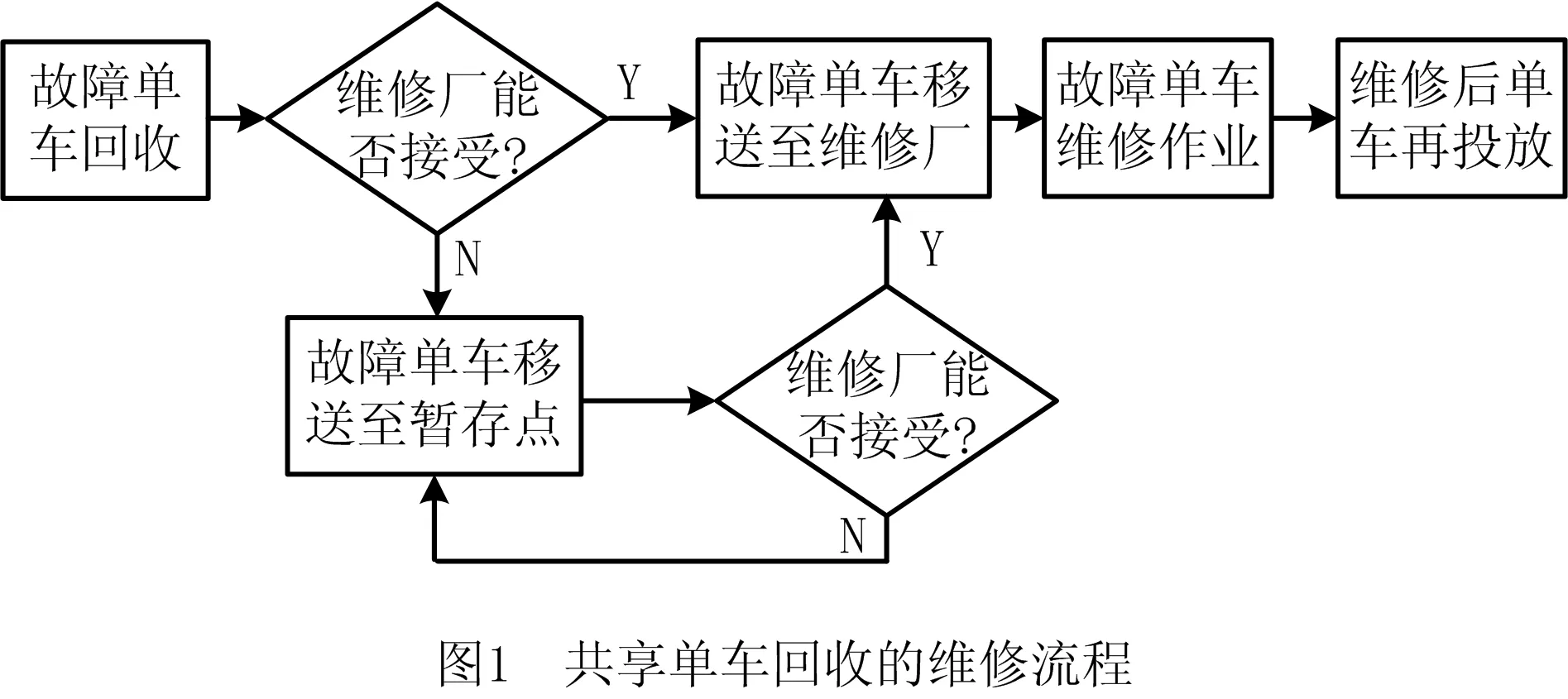
根据是否设置暂存点,各运营片区的故障单车回收运输策略分为以下3种:①不设置暂存点的直运策略;②设置暂存点,且所有故障单车均要通过暂存点的转运策略;③设置暂存点,部分故障单车直接运输到维修厂,部分故障单车经过暂存点后再转运至维修厂的混合策略。直运和转运策略又统称为纯策略。故障单车全网络的回收运输策略集合也有3种情况:①所有片区都是直运的直运策略集合;②所有片区都设置暂存点,都采用转运的转运策略集合;③部分片区直运而部分片区转运的多策略集合。直运策略集合和转运策略集合又统称为单策略集合。
在多对多网络中使用合并终端(相当于枢纽)的一个重要原因是成本降低,最佳组合取决于合并收益和惩罚之间的权衡[18-19]。共享单车企业在城市中回收故障单车,与汽车、铁路运输和航空业不完全相同,因为这些行业的运输负荷较大,货物合并更为经济。故障共享单车回收中设置的暂存点,同时具有HALL[16]提出的库存合并和终端合并的特征。库存合并涉及将不同时间段发现的故障单车合并到同一负载中(时间合并),而终端合并将来自不同位置的项目合并到同一负载中(空间合并)。与其他研究不同的是,故障共享单车回收中设置暂存点,优先考虑城市物流和维修厂能力存在的时间和空间限制,以及共享单车企业的服务水平。目的是促进故障共享单车的及时清运和维修。此外,若一个城市只有一个维修厂,网络是多对一的。
共享单车企业使用专用运输卡车对故障单车进行收集后,直接运往维修厂,或存放到暂存点后再运往维修厂,有满载和最优装载量两种装运方式。满载是指装运卡车按最大装运量进行运输。如果不是满载装运,会增加运送的次数,但能降低滞留在区域内现场或暂存点的故障单车数量,理论上就存在一个最优装运量,使回收总运营成本最小。
1.2 符号描述
本文模型中涉及的参数和符号定义如表1所示。

表1 主要参数和符号
表中:z=1,2,3分别表示各运营片区中直运、转运和混合策略;N=Ⅰ,Ⅱ,Ⅲ分别为全网络中直运策略集合、转运策略集合、部分片区直运而部分片区转运的多策略集合。时间段i=1,2,…,n,运营片区j=1,2,…,y。
部分参数说明如下:
(1)每趟卡车运输距离d,指一辆故障单车从被发现到维修完成后再投放,各个环节所有运输距离之和。
(2)平均静态储存时间ts,指一辆故障单车从被发现到维修好后再投放,整个过程中除在途运输时间tm和维修时间之外的等待停留时间,例如在暂存点的停留时间和在维修厂等待维修的排队时间。同一种装运方式下,3种回收策略的平均静态储存时间相同。但最优装运量比满载情况下的平均静态储存时间要短。
1.3 模型假设
本文的基本假设说明如下:

假设2单车企业无论采用何种装运方式和回收策略,服务水平都应大于最低服务水平α*,即α≥α*。某区域某共享单车企业的服务水平受用户骑行需求满足率,以及发现故障单车概率的共同影响。为了避免低于最低服务水平,根据服务水平的定义,企业可以通过投入新的共享单车增加某区域内某企业可用的单车数量G,也可以迅速清运某区域内故障单车,降低用户使用到该企业故障单车的概率β来实现。
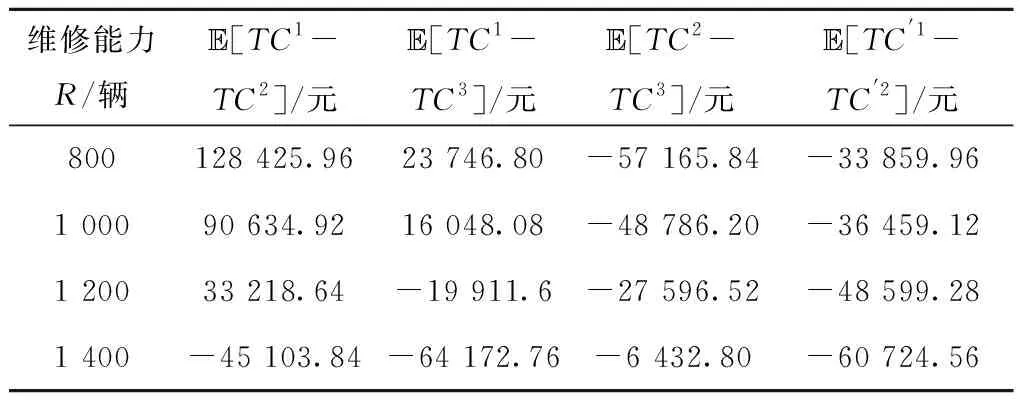
假设3最优装运量下运输故障单车的卡车装载量不超过卡车的最大装载量,即v* 一个运营周期内故障单车维护修理的总运营成本为: (1) 满载装运下,直运策略只有维修厂,TK1=K;转运策略和混合策略,都有维修厂和暂存点,TK2=K+Kw,TK3=K+Kw。3种回收策略下的总运营成本分别为: (2) (3) (K+Kw)。 (4) 由式(2)~式(4)得到满载下,运营片区中3种回收策略之间的总运营成本差的期望值分别为: cnμDα*ξ(δ)Б1-2-Kw, (5) (6) (7) 命题1混合策略只会是次优策略,至少有一种纯策略会优于混合策略,当维修能力一定时,随着维修延误率的增大,直运会变为转运。 命题1表明,相比混合策略,直运和转运策略不仅具有系统运行和管理上的简便与稳定等优势,更重要的是直运策略没有暂存点的固定设施费用,而转运纯策略更能充分发挥暂存点的规模效应。暂存点一般是租赁空闲厂房或闲置土地,相比运输费用,租赁费依然不容忽视。因此,不能充分利用暂存点规模效应,且有暂存点固定设施投入的混合策略,不可能同时优于直运策略和转运策略。因此,片区中回收策略的决策只需要在直运与转运这两种纯策略中进行选择,这也与BLUMENFELD等[18]对通用汽车的案例研究结论一致,符合NEWELL[38]提出的“全有全无(all or nothing)”法则。当故障单车维修延误率较低时,片区回收的总运营成本也较低,不用设置暂存点就可以保持一定服务水平。维修能力一定的情况下,随着维修延误率增大,片区回收的总运营成本也升高。当维修延误率大于直运—转变云临界维修延误率时,片区大部分故障单车不能及时维修,只能通过设置暂存点存储故障单车,缓解维修压力,才能不低于最低服务水平。片区内设置转运点,及时清运故障共享单车,可以有效降低新车购置成本。此时,转运比直运有效降低的新车购置费用,可以抵消新增暂存点的固定成本和绕行增加的运输费用。 (8) cnμDα*ξ(δ)Δv2Б1-2-Kw。 (9) 基于命题1的结论,已知混合策略不是最优策略,只需对满载和最优装运量下转运和直运两种纯策略进行比较,于是得到命题2。 命题2最优装运量比满载更能有效缓解维修压力,能在更大的维修延误率下仍保持一定的服务水平,即相比满载,最优装运量方式下的直运策略选择区间更大。 这是因为更高的运输频次能更快速地清除现场的故障单车,用户使用到故障单车的概率下降,为维持服务水平而购置新单车费用降低。因此相比满载,最优装运量方式通过更高的运输频次缓解了部分维修压力,能在更大的维修延误率下仍保持一定的服务水平。 根据前文所述,相同策略下最优装运量比满载有成本优势。同时,由命题1的结论可知,最优回收策略只在直运与转运两种纯策略之间选择,因此在命题2的基础上,得到命题3。 命题3相同纯策略下,维修延误率越大,最优装运量比满载的成本优势越大;且随着维修延误率的上升,直运下最优装运量比满载的成本优势,比转运下增长的幅度更大。 证明在纯策略下比较满载与最优装运量下总运营成本差的期望值: (10) 维修延误率ξ(δ)增大,用户使用到故障单车的概率β增大,保持最低服务水平需要的新单车数量也增加。因为最优装运量比满载的运输频次更高,共享单车企业在最优装运量下可以比满载下能更迅速地清运现场或暂存点的故障单车,降低了用户使用到故障单车的概率β,减少了为保持最低服务水平而额外购置新单车的费用,改善了总运营成本。这种改善对利用暂存点储存故障单车的转运策略来说差异不大,而对直运策略来说成本改善更明显。或者说,维修延误率越大,相比转运,直运总运营成本对装运量的敏感性越高。 共享单车公司在运营一般不会跨运营区域进行故障单车回收,同时在某片区内的故障单车回收有相对固定的路线,运输车辆在网络中的运输距离也可以近似用线性表示。文献[18]证明了运输网络的成本可以近似用数个子网络的成本加和,因此故障单车回收维修的全网络,可看作y个单片区和固定设施共同构成。 根据命题3,最优装运量更具成本优势。因此,当采用最优装运量时,全网络回收策略集合N下总运营成本为: (11) 命题4维修能力一定情况下,随着故障单车维修延误率的上升,整个运营网络的最优回收策略集合,将由(最优装运量,直运)单策略集合,变为(最优装运量,直运)和(最优装运量,转运)并存的多策略集合,最后变为(最优装运量,转运)单策略集合。 证明(最优装运量,直运)单策略集合和(最优装运量,转运)单策略集合下,全网络总运营成本的期望值分别为: (12) (13) (最优装运量,直运)和(最优装运量,转运)并存的多策略集合下,设j=1,2,…,x的片区采用直运,j=x+1,x+2,…,y的片区采用转运,全网络总运营成本期望值为: (14) 由式(12)~式(14)可得,(最优装运量,直运)单策略集合和(最优装运量,转运)单策略集合之间、(最优装运量,直运)单策略集合和多策略集合之间、(最优装运量,转运)单策略组集合和多策略集合之间的全网络总运营成本差的期望值为: (15) (16) (17) (18) (19) (20) 综上,当维修能力一定时,一般在运营早期,单车故障率较低,全网络回收维护的总运营成本低,所有片区都不需要设置转运点,(最优装运量,直运)单策略集合就可满足一定的服务水平。随着维修延误率上升,全网络回收维护的总运营成本也会升高。通过调整维修厂分配给各片区的维修能力,尽可能满足多数片区直运策略的条件,少部分片区则设置转运点变为转运策略,即(最优装运量,直运)和(最优装运量,转运)并存的多策略集合。这样既能控制全网络暂存点的固定设施总费用,又可以充分发挥暂存点的规模效应,从而在一定服务水平下控制整个网络的总运营成本。若单车维修延误率继续上升,而维修厂能力不能满足所有片区维修需求时,就只能在所有片区都设置暂存点,全网络回收维护的总运营成本也会继续升高。此时采用(最优装运量,转运)单策略集合,才能满足一定的服务水平。 需要说明的是,全网络中多策略集合与命题1中的混合策略不同,混合策略是一个片区内部分故障单车通过暂存点转运后再运到维修厂,一个片区内采用混合策略,暂存点并不能发挥规模效应。而全网络多策略集合下,只有部分维修延误率高的片区设置暂存点,采用的是转运纯策略,暂存点可以充分发挥规模效应,因此与命题1是一致的。 下面基于美团单车成都公司的调研数据和合理假设,以一个运营周期内4个时段(i=4)为例进行计算。一辆运输卡车的最大装载量V=60辆,单次卡车出车费用为cf=100元,运输卡车单位距离运费cd=0.81元/km,每辆单车单位时间在途储存成本cm=0.02元/km·辆,直运的平均距离d1=9.3 km,转运的平均距离d2=18.6 km,直运和转运策略平均在途运输时间差Δtm=-1.8 h,单位新单车购置成本cn=600元/辆,最低服务水平α*=0.9,混合策略中采用直运的比例为γ=0.3。β1=0.043,β2=0.032,β3=0.038分别表示满载时直运、转运与混合3种回收策略下顾客使用到故障单车的概率。β′1=0.032,β′2=0.025分别是最优装运量下直运和转运纯策略初始时刻顾客使用到故障单车的概率。共享单车骑行需求和故障数量分别服从正态分布D~N(16 000,2 400),Q~N(1 200,150)。暂存点在一个运营周期内的固定费用Kw=1 5000元。求得运输卡车的最优装运量v*=48辆,将数据代入式(5)~式(7)和式(9),在不同的维修能力R下分别得到满载时直运与转运、直运与混合、转运与混合策略运营成本差的期望值,以及最优装运量下两种纯策略运营成本差的期望值,计算结果如表2所示。 表2 不同维修能力下不同回收运输策略 运营成本差期望值的比较 表2的计算结果显示,当维修能力R较小,共享单车企业的故障单车剩余维修能力δ<0(δ=R-μQ)时,说明不能及时维修所有故障车,维修能力不足。对应表2中R=800,R=1 000时,有[TC1-TC2]>0,[TC1-TC3]>0,说明此时满载下的直运策略运营成本期望值大于转运和混合策略;[TC2-TC3]<0则表明此时转运的成本期望值小于混合策略;且有[TC1-TC2]>[TC1-TC3]>[TC2-TC3],表示转运策略的总运营成本期望值最低,混合策略次优,直运策略成本总运营成本期望值最大。当维修能力R较大,维修能力达到和超过故障单车的平均数量,故障单车剩余维修能力δ≥0,对应表2中R=1 200,R=1 400时,有[TC1-TC2]<[TC1-TC3]<[TC2-TC3],说明此时,满载下的直运策略更有成本优势,混合策略次之,转运策略总运营成本期望值最高。上述结果从数值上也证明了纯策略总是优于混合策略,且随着维修能力富余的减小,转运的成本优势更加显著(命题1)。 相同回收策略下,满载和最优装运量的平均静态储存时间差都设为Δts=1.5 h,单位时间每辆故障单车的静态储存成本cs=0.062 5元/h·辆,其他参数不变,代入式(10)得到结果(如图4)。 图4中展示了直运与转运策略下,满载与最优装运量的总运营成本差的期望值都[TC1-TC′1]>0,[TC2-TC′2]>0,说明最优装运量比满载更有成本优势。而且[TC1-TC′1]和[TC2-TC′2]都随维修延误率单调递增,表示相同纯策略下,维修延误率越大,最优装运量比满载的成本优势越大(命题3)。图4还显示,随着维修延误率增大,[TC1-TC′1]以及[TC2-TC′2]之间的差距也越来越大,说明随着维修延误率增大,相比转运策略,直运策略下最优装运量比满载更能节省成本(命题3)。 本文从共享单车回收维修业务现状出发,对共享单车企业故障单车回收策略和装运方式进行研究,期望改善运营成本,提高服务能力,从而提高企业的市场竞争力。在一定服务水平下,以总运营成本最小为目标,研究了故障共享单车的回收策略和装运方式,以及两者的最优组合。 研究结果表明: (1)无论是满载还是最优装运量进行装运,至少有一种纯策略会优于混合策略,且维修延误率越大,转运策略更优。说明混合策略既要支付暂存点固定设施费用,又不能有效利用暂存点的规模效应,最多只能成为次优策略。当维修延误时率越大时,转运策略通过暂存点可以缓解维修压力。 (2)相比满载,最优装运量方式下的直运策略区间更大,最优装运量方式通过更高的运输频次缓解了部分维修压力,可以承受更大的故障单车维修延误率。 (3)最优装运量方式比满载更有成本优势,且这种成本优势随维修延误率单调递增,直运策略更能在最优装运量方式下获益。 (4)在采用更有成本优势的最优装运量的基础上,对每个运营片区的直运和转运策略进行选择,能够得到使全网络总运营成本最小的最优策略组合集合。当维修能力一定时,随着故障单车维修延误率的上升,全网络的最优回收策略集合将由(最优装运量,直运)单策略集合变为(最优装运量,直运)与(最优装运量,转运)并存的多策略集合,最后变为(最优装运量,转运)单策略集合。 本文研究对共享单车企业更好开展故障单车回收维修业务,改善运营成本,提高服务能力,有以下启示: (1)随着共享单车企业运营时间的延长,共享单车故障率上升,必然会导致单车维护修理运营成本的上升。一方面可以加大投入提高维修厂的维修能力;另一方面,随着共享单车故障率的上升,若不能及时提高维修能力,共享单车企业倾向采用(最优装运量,转运)的策略。即通过更高的运输频次,以及增设暂存点来迅速清运现场的故障单车,降低用户使用到故障单车的概率,从而有效保持一定服务水平,并缓解维修压力。即使未设置暂存点,直运策略下采用更高的运输频率也能有效降低总运营成本。 (2)引入外部资源提高维修能力的柔性,将有助于共享单车企业提高服务水平。单车企业设置的维修厂具有相对稳定的维修能力,并不能很好应对波动的维修需求。共享单车企业可以尝试利用外包的形式来提高维修能力的柔性。当维修厂维修能力闲置时,则承接其他企业的维修业务。 (3)对骑行需求及共享单车故障率等运营数据的采集分析,能有效改善共享单车企业回收维修业务的运营成本。在运营初期,共享单车企业没有足够的运营数据,无法对骑行需求和故障率做出准确的预测和判断。随着实际运营数据的积累,共享单车企业可以在实际数据支持下进行回收策略和装运方式的决策,从而改善运营成本,也能合理设置和调整维修厂的维修能力。大样本的数据还可以指导下一代共享单车的设计,通过设计和工艺降低单车的故障概率,从而更有效地改善回收维修业务的运营成本。 在对共享单车回收维修业务后续的研究中,可以考虑分析维修能力变化对运输时间、储存时间、维修时间等参数的影响,或是更进一步考虑单车更新换代的情形。此外,回收系统中跨运营区域的运力调配组合与最优设施能力的确定也是值得探讨的方向。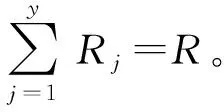
2 单运营片区系统中回收策略研究
2.1 满载下的回收策略研究

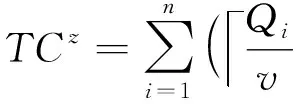
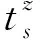
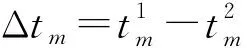

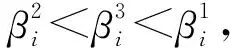

2.2 最优装运量下的回收策略研究
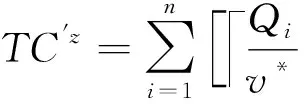
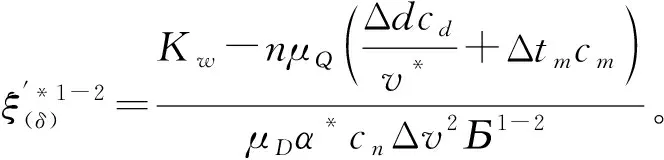

2.3 两种装运方式的比较
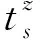
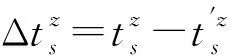
3 全网络回收策略研究



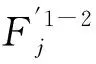
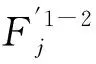
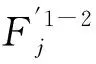
4 数值分析

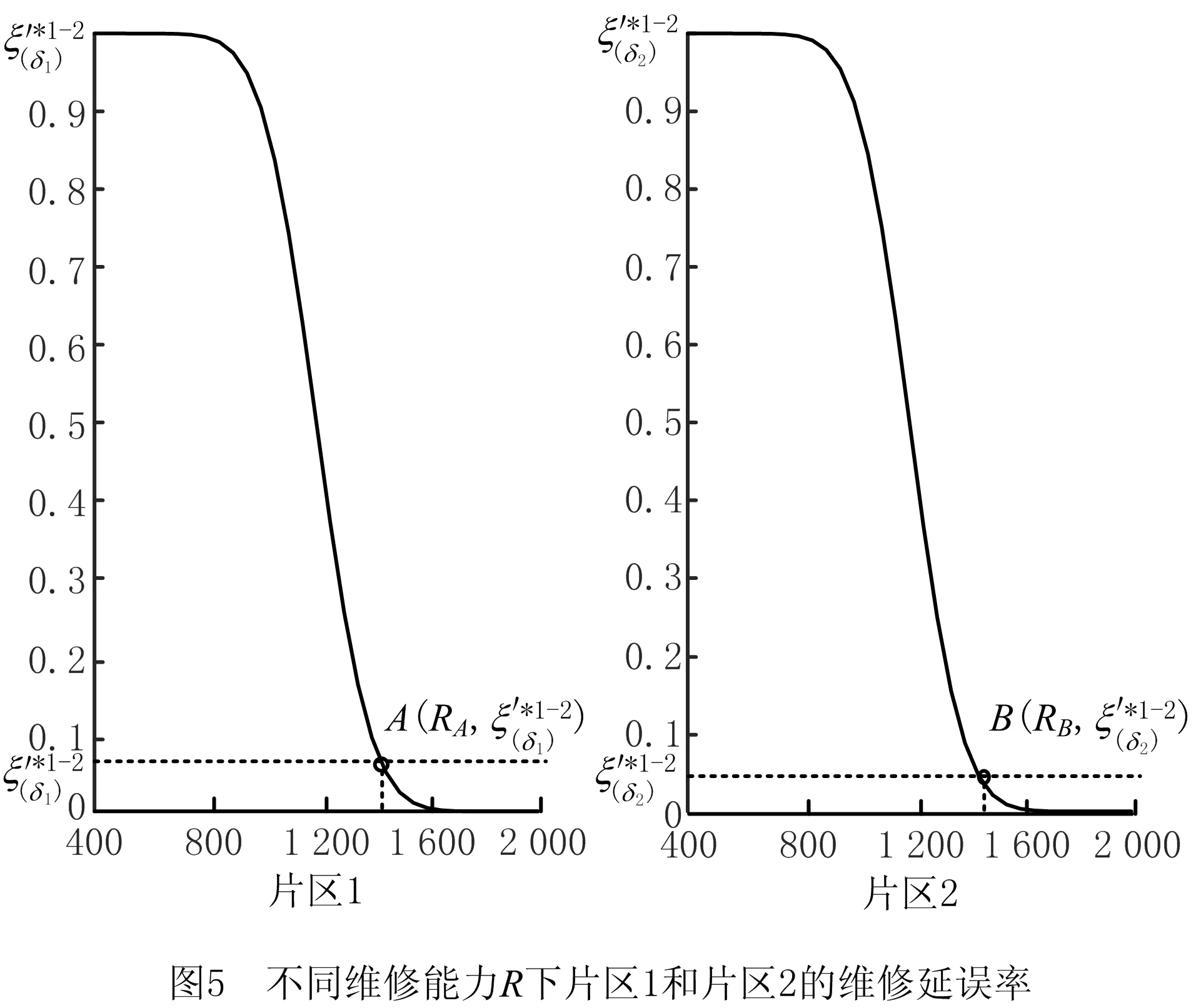
5 结束语
——美国下篇

