B样条曲面与点梯度源构建功能梯度材料模型
韩 硕,周 婧,彭壮壮,韩晓伟,王世杰,段国林+
(1.河北工业大学 机械工程学院,天津 300401;2.承德应用技术职业学院 智能制造系,承德 067000;3.天津科技大学 机械工程学院,天津 300222)
0 引言
功能梯度材料(Functionally Graded Materials, FGMs)是构成材料的要素(组分、结构)在空间呈梯度变化,从而使材料的性质和功能也呈梯度变化的一种先进工程材料[1]。由于功能梯度材料具备优异的功能特性,已成为国内外的研究热点。自提出至今,在建筑、机械、医疗、国防、军事、半导体、航空航天等众多领域,都有较高的利用价值与广阔的应用前景[2]。
增材制造(3D打印)技术是一种数字化的添加材料成形技术,对材料成分、组织结构具有潜在的控制能力,成为最具潜力的功能梯度材料制造方法[3]。但在功能梯度材料的模型建立上仍需要进行深入研究。目前功能梯度材料的模型建立,主体上可以划分为两个方向,分别为几何空间内的三维实体模型的建立与材料空间内同种或多种材料的合理分布。近年来,有关功能梯度材料的建模方法被相继提出,KUMAR等[4]提出利用几何信息与材料信息进行布尔运算,扩展rm-sets的非均质实体建模方法;YOO[5]提出基于径向基函数的非均质材料表示方法,通过材料函数映射至几何体的方法,表达非均质体模型;JACKSON等[6]利用有限元思想,通过将模型离散化成四面体单元的方法,将零件模型与材料分布信息赋予至单元节点中;KOU等[7]提出采用边界对几何体建模,利用异质特征树的方式表达材料分布;YANG等[8]提出基于B样条曲线的功能梯度材料模型的设计方法,通过放样的方法将非均质体材料赋予至几何模型中,可以精确表达出其材料在非均质实体中的分布情况;OZBOLAT等[9]通过建立Voronoi图与参数化距离的加权方法,把功能梯度材料的材料分布映射至几何空间中,实现功能梯度材料的多孔结构的建模;GUPTA等[10]利用梯度参考来表示复杂的非均质材料几何模型;吴晓军等[11]提出一种体素化功能梯度材料建模方法,将CAD模型离散体素化后与其目标材料信息相结合,生成体素化模型;朱玉芳等[12]提出基于STL(stereolithography)面化模型的微四面体非均质材料零件建模方法;周满元等[13]提出一种表示功能梯度材料模型的扩展B-Rep模型的建模方法。
目前,大部分方法都是针对特定的研究对象和需求展开的,只能设计制造简单梯度材料。研究复杂梯度材料3D打印技术,实现材料多维空间的非线性梯度分布,以满足各种实际工程需要的功能梯度材料模型的构建方法还有待深入研究。
1 功能梯度材料建模
1.1 功能梯度材料映射
功能梯度材料的建模主要包括几何信息的构建和材料信息的构建两方面内容。其中几何信息是在几何空间中利用CAD软件构建三维几何模型完成的,材料信息是通过理想材料的空间分布设计完成的。
定义几何空间G,建立零件几何模型,然后在材料空间根据材料结构设计得到的梯度变化模式确定材料模型和映射关系Φ,从材料空间以映射关系Φ将材料模型映射到几何空间,从而构建出功能梯度材料三维模型,如图1所示。
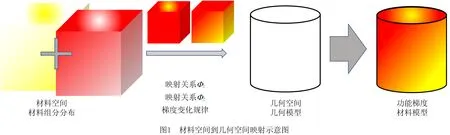
1.2 功能梯度材料建模复杂度分类
根据从材料空间到几何空间映射的复杂程度,可以将功能梯度材料建模分为以下3种主要情况:
(1)材料组分以单一函数规律变化的简单梯度模型
这种情况一般适于几何形状比较简单、材料变化规律单一的模型。如图2所示,预打印的条块由两种材料组成,按颜色区分即由紫色和蓝色组成。紫色材料的体积分数用函数f表示。相对应的蓝色材料的梯度变化规律为1-f。函数f和1-f构成了映射关系Φ。
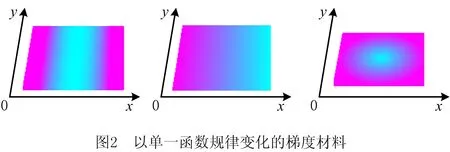
(2)材料组分以多个函数规律变化的梯度模型
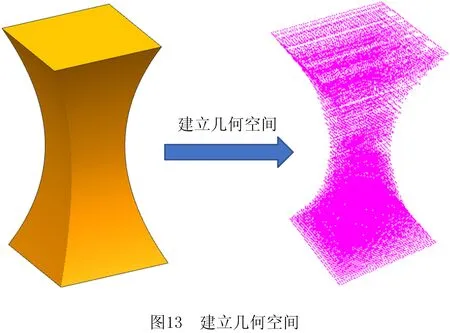
有些材料变化较复杂的模型仅由一个映射关系来表示是不够的。如图3所示,对不同的区域,要分别确定相应的映射关系Φ1,Φ2,…,Φi,…,Φn,不同区域的点通过不同的映射关系实现对材料组分的映射。

(3)无函数规律的梯度模型
更为复杂的材料变化情况难以找到可以精确表达其变化关系的函数。如图4所示,映射关系只能用离散的方式来表示,计算机将每一个映射关系信息存储起来。

通过以上分析,除第3种情况外,都可以根据实际需要,设计功能梯度材料从材料空间到几何空间的映射关系,而第3种情况虽然没有具体的映射规律,也可以认为由多个映射关系相互影响而形成的。因此,利用将点梯度源分散放置在B样条曲面的节点上,并通过其相互影响的方法建立无映射规律的梯度模型。每一个梯度源的映射关系Φ对应着一个F(x,y,z)函数。
F是一个由一组材料组分梯度变化规律函数构成的向量。
(1)
式中fi(x,y,z)表示第i个材料组分在(x,y,z)处的分布规律,即体积分数。各个材料在空间某一点处的体积分数之和等于1,即
(2)
2 功能梯度材料设计
在材料空间内,根据设计曲面插入多个可调控的点梯度源建立材料模型,可以实现三维空间内的材料变化,并根据多种变化规律的点梯度源相互影响,共同映射成复杂材料模型。
2.1 B样条曲面
在材料空间中建立一张p×q次张量积B样条曲面由相互垂直的两向网格由(n+1)×(m+1)个控制顶点和节点矢量构造。B样条曲面内的任意点可由式(3)获得:
U=[u0,u1,…,um+p],
V=[v0,v1,…,vn+q]。
(3)
式中:P为实体模型上点的位置向量;u,v为相互独立的参数;Pi,j为B样条的控制顶点;p和q分别为B样条基函数Ni,p和Nj,q在u和v方向上的阶数。
如图5a所示为一个双四次B样条曲面片,其中Pi,j为自定义设置的控制节点,用于调控张成B样条曲面的基本形状;图5b为双六次B样条曲面片,黑色网格线为控制点组成的控制多边形,而彩色的密致网格曲面为控制点所张成的B样条曲面,色彩网格的交点为生成矢量节点。
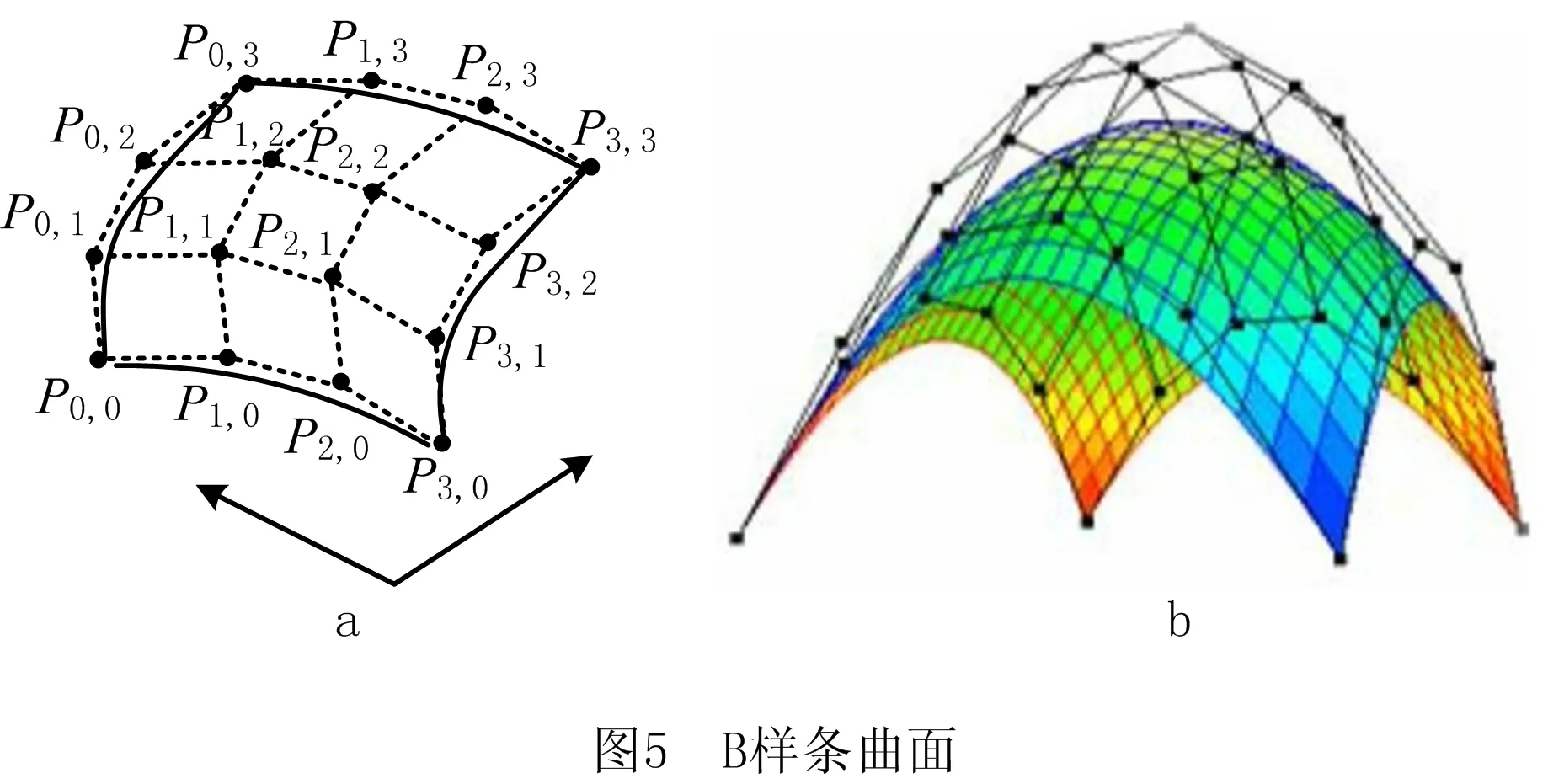
2.2 点梯度源映射模型
SIU等[14]针对功能梯度材料零件的CAD模型,提出梯度源(source-base)模型,如图6所示。梯度源以零件内部某一点作为某一种材料的“发源地”,以点、线、面任意一个几何固定特征为载体,用空间中点P到梯度源的距离d作为变量来设计材料的变化趋势,用距离函数f(d)来表示零件上该点材料的组成。距离函数f(d)(d∈R)是单元体中某点到梯度源中心距离的函数,用来控制材料的梯度变化,其中材料分布函数可以是线性的也可以是非线性的,不同距离函数对应不同材料分布曲线。利用该方法产生一块材料具有连续梯度变化的区域。
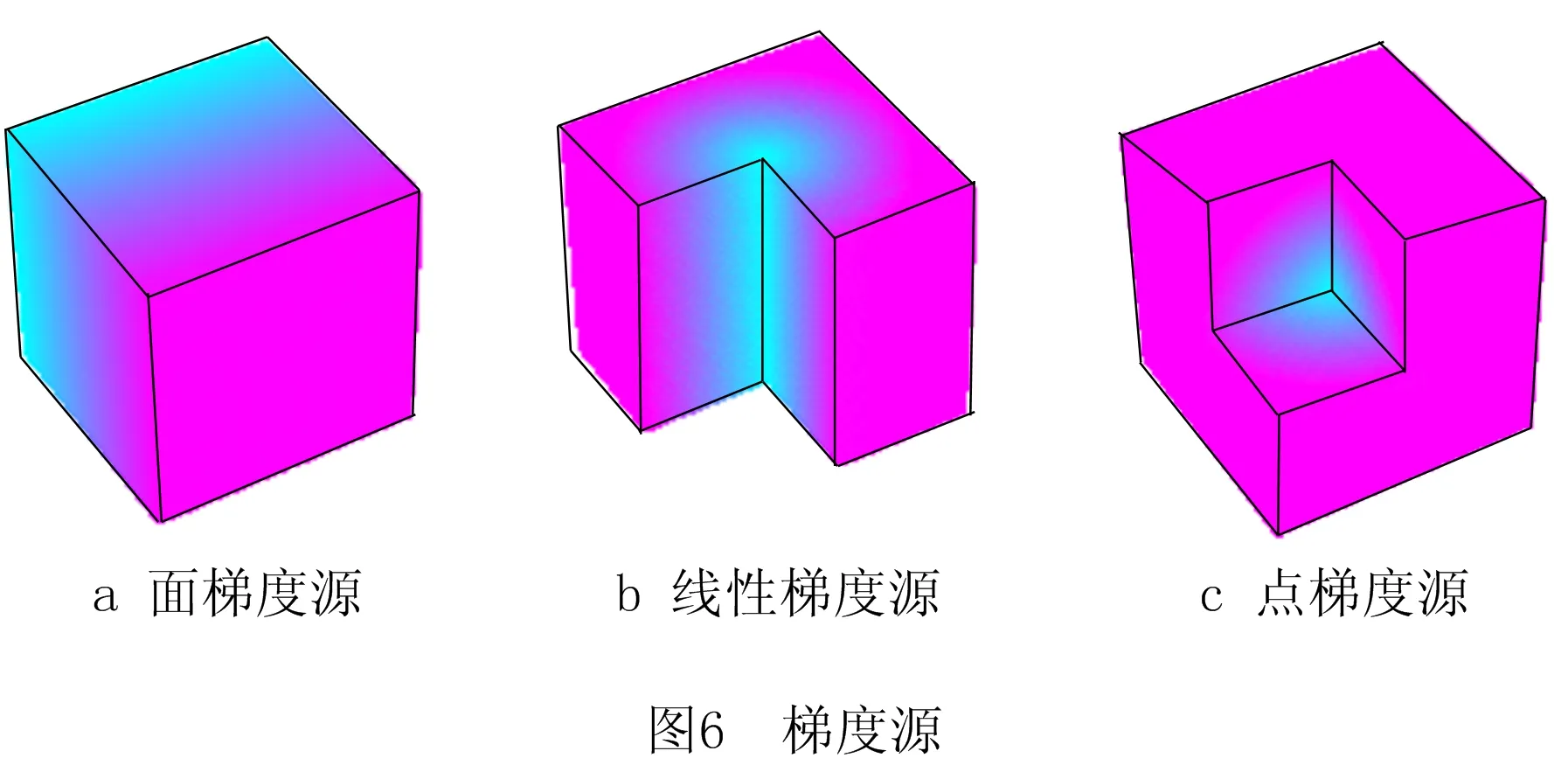
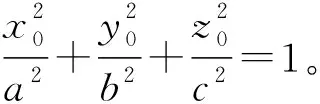

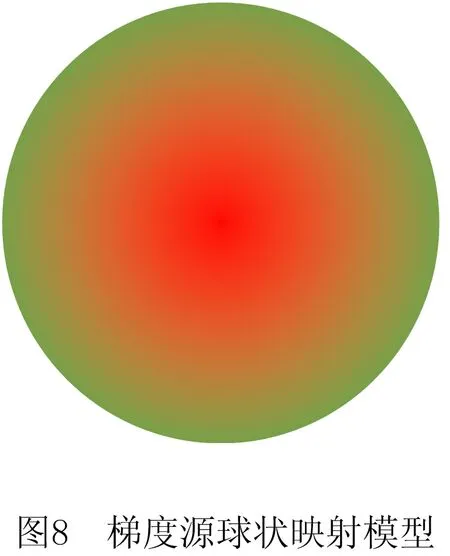
以图8所示球体点梯度源为例,该梯度源球状映射模型由A与B两种材料组合而成。假设球心O处的成分由体积分数为100%的红色材料A与体积分数为0%的绿色材料B组成。由该O点处向周围空间均匀散射长度为r的有向线段,方向由O点指向有限线段终点。在单一条有向线段上符合材料分布函数f(d)=d,A材料的体积百分比由O处的100%沿着线段方向映射衰减至线段终点处0%,同时绿色材料B的体积分数,沿着线段方向由0%增幅至100%。形成一个以空间中某点O处为球心,半径长度为r的致密实心球体,且在任意一点处,红色材料A与绿色材料B的体积之和相同,满足式fA+fB=1。
在材料空间中将建立好的梯度源模型中心放置于B样条曲面的节点位置,构建材料分布结构,如图9所示。

3 几何模型分层处理
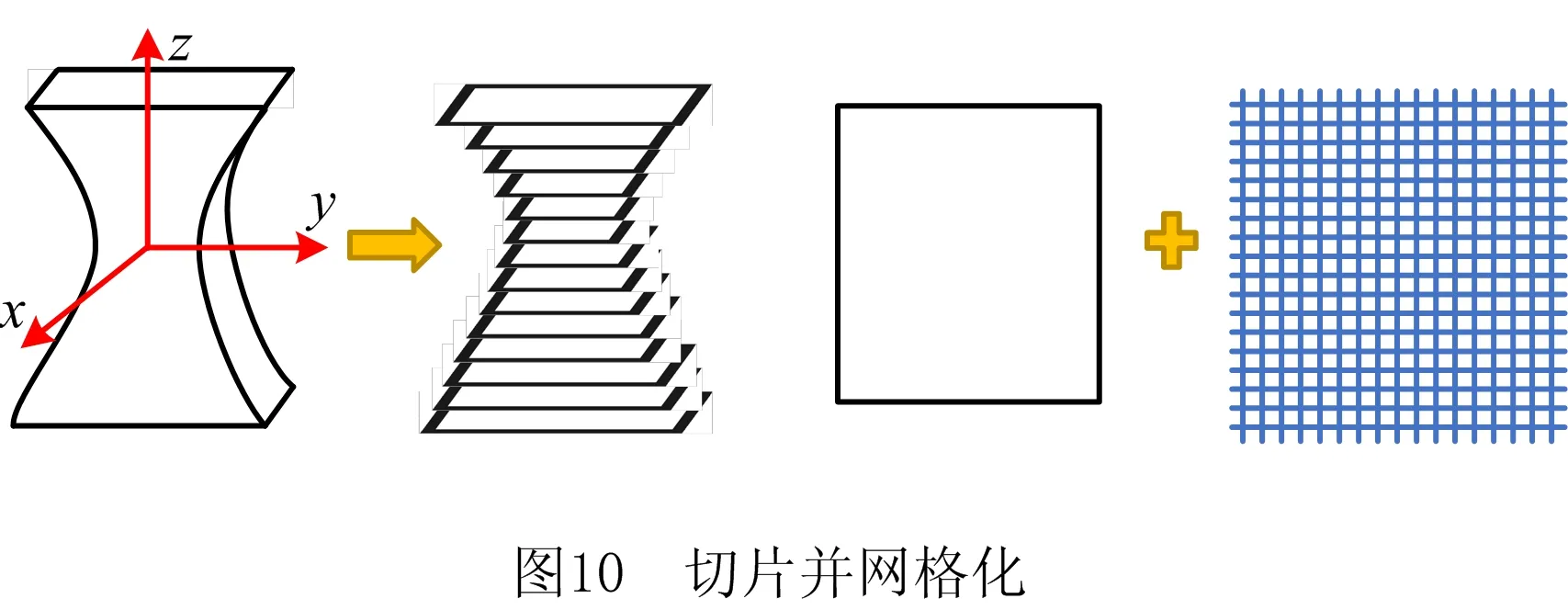
将模型的STL文件导入由团队以VisualStudio 2019为平台自行编写的切片软件中,进行分层切片,再根据打印需求设计好层高后,可将模型用多层轮廓线表示,并利用OpenGL可视化功能将其展示出来。在得到每一层的轮廓切片后,将其内部填充区域网格化,单元网格的长宽根据自身的打印条件进行设计。宽度由打印机设定挤出丝宽度与挤出胀大现象综合考虑后设计,长度由打印机的打印分辨率大小进行设计。打印分辨率是指打印机挤出头混料机构将多种材料混合到满足均匀度要求所需时间内挤出头移动的最短距离。根据实际需求设计网格化轮廓切片,为了便于展示,将其网格均匀化,如图10所示。
将模型轮廓切片后进行网格化,由图11可得出该打印填充区域存在着3类交点:
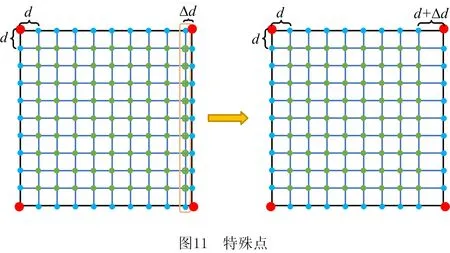
(1)交点类型一:轮廓线与轮廓线间的交点,该交点是对模型切片时产生的用于组成模型轮廓的拐点,起到3D打印时识别模型轮廓信息的关键标识点的作用。
(2)交点类型二:横纵线的交点生成单元网格的顶点,该交点作为打印区域内部的识别点,在3D打印过程中起到作为含有材料信息的打印路径点的作用。
(3)交点类型三:横纵线与轮廓线的交点,该交点在模型轮廓线上,是3D打印过程中打印模型边界轮廓含有材料信息的路径点。
综上可知,在生成第三类型交点时,存在着两点间距离小于打印分辨率距离的交点,当出现此类交点时要根据相邻点间的重要程度,去除不可以打印的无效交点。并把剩余的有效交点按照自定义的打印顺序进行路径规划并存储起来,成为3D打印过程中的路径点,如图12所示。
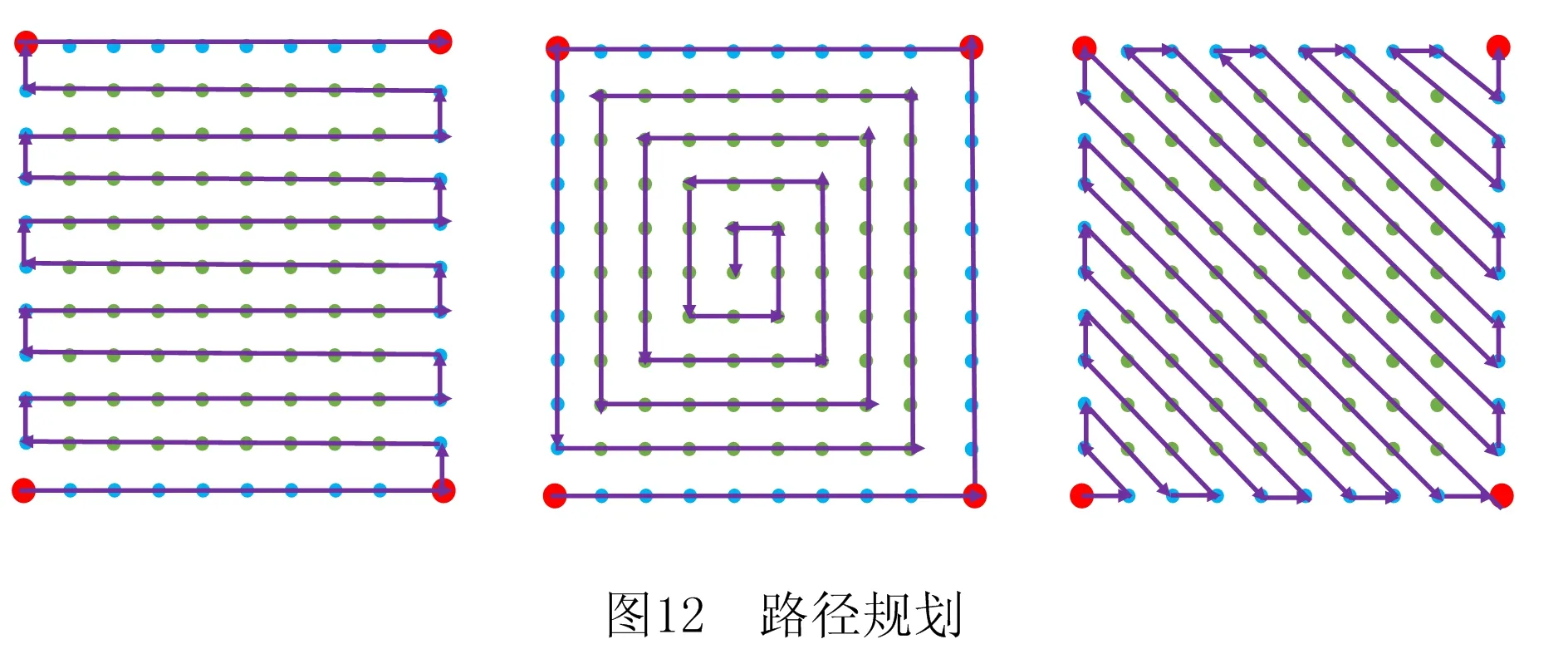
每一层切片通过建立网格,去除无效交点,形成打印路径点后,将所有的路径点按所属层进行堆积,用来还原几何实体模型,形成由路径点充斥而成的三维实体,由此来建立几何空间,为材料映射作准备,如图13所示。
4 建立映射
4.1 被映射点体积分数计算
在由路径点所组成的几何空间中仅包含模型所在的几何笛卡尔坐标系下的几何坐标信息,还未被赋予具有梯度变化的材料信息。因此,建立映射函数,把点梯度源的球状映射模型中心放置于几何空间中,如图14所示。以函数映射的方式对以O为球心、r为半径的区域内所有路径点赋予上材料信息。
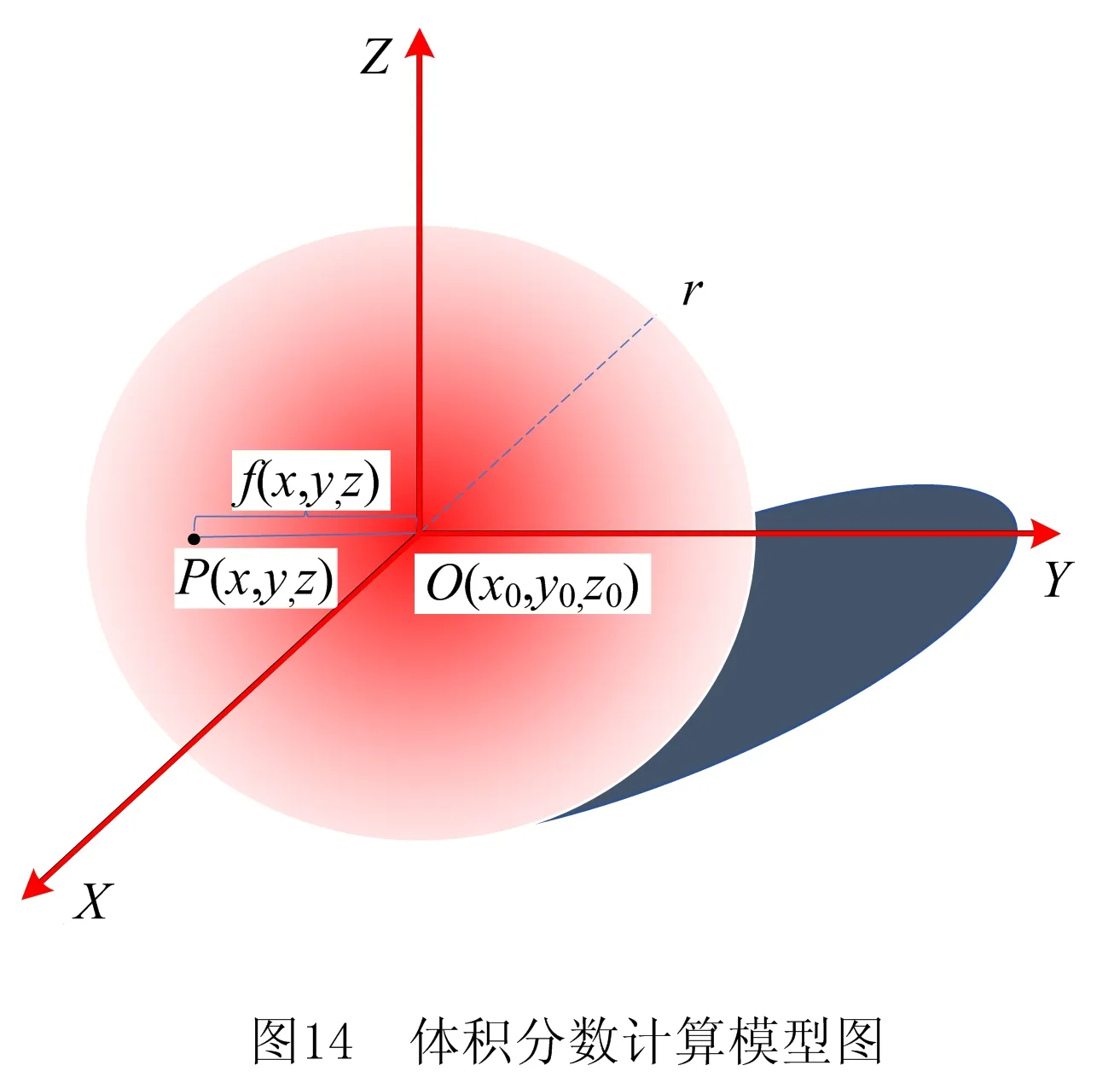
以模型空间内某一点O(x0,y0,z0)为球心,r为半径,在该完整的球状映射域所包含到的路径点将按照下述式(4)与式(5)映射其材料信息。
利用空间中点到点间距离公式求取,模型中某一路径点P(x,y,z)到球心O间的距离,并用计算出的距离与映射半径r的比值关系来表示某种单一材料A的体积分数。
模型中任一路径点至梯度源处距离:
f(x,y,z)=
(4)
建立映射函数求得该路径点处材料A的体积分数:
ηA=(r-f(x,y,z))/r。
(5)
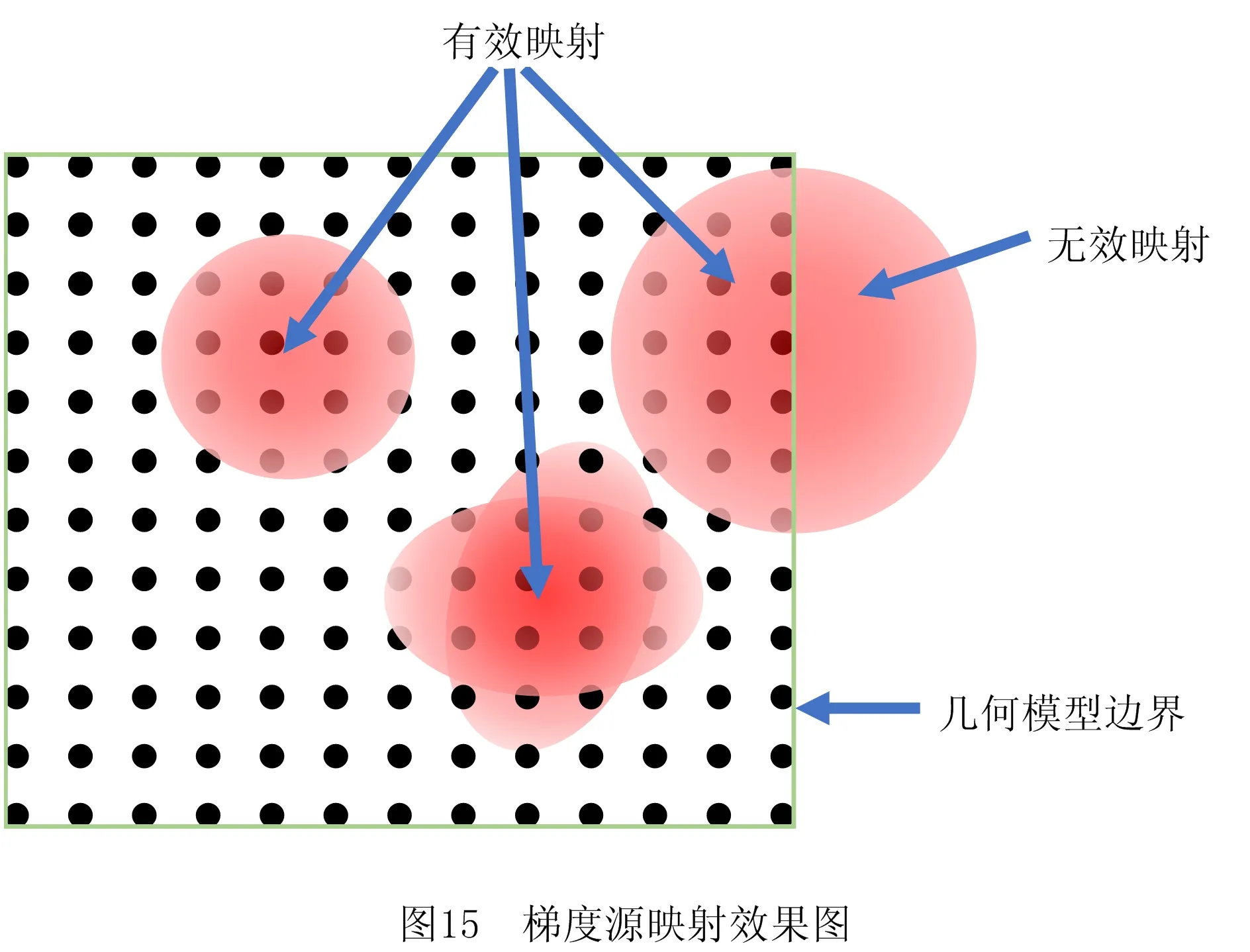
如图15所示,通过改变梯度源的半径r大小,可以直接影响映射范围内的点上的材料体积分数。根据空间映射理论,在梯度源所映射到的路径点,材料的体积分数具有梯度变化,没有在映射范围内的路径点,其材料的体积分数设置为0%。
4.2 叠加效应映射
如果需要构建的梯度材料模型变化趋势复杂,无法使用单一点梯度源模型来表示,可以通过多个梯度源的相互叠加组合来表示复杂模型。
如图16所示,当某一路径点被两个或两个以上的梯度源映射到时,利用其分别所处梯度源的体积分数进行线性求和。该路径点的单一材料体积分数为多个体积分数之和,且叠加上限不超过100%。

体积分数线性叠加公式如下:
(6)
图16中,点1处为球心,材料体分比为100%;点2处为梯度源半径中心处,材料体分比为50%;点3处为梯度源边缘处材料体分比为0%;点4处既为梯度源的半径中心处又为另一个梯度源的边缘处,材料体分比为50%+0%=50%;点5同点4处相同,材料体分比为50%;点6处位于球心,材料体分比为100%;设点7处同点2处相同,材料体分比为50%;点8处位于两梯度源半径边缘处材料体分比为0%+0%=0%;设点9处同既属于球心处也属于半径边缘处,材料体分比为100%+0%=100%;当出现A%+B%≥100%时,视该点的材料体分比为100%。
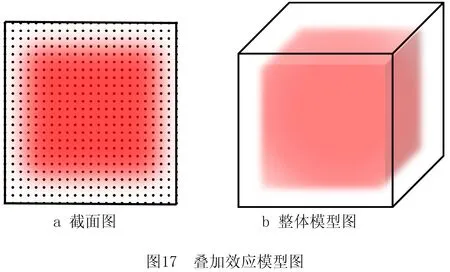
利用上述叠加原理,在几何空间内指定点或区域安置点梯度源模型群,通过相互叠加影响使多个球体边界相互叠加,形成包络面来自定义建立材料变化模型,再映射至几何空间可实现多种变化规律。如图17所示,其模型为内部为某一种材料的立方体,外部为另一种材料,两者交融处产生材料的过渡变化。为方便表示,选用截面图,深色为材料空间中的某一材料结构分布,无色表示另一种材料,黑色点表示几何空间中路径点,黑色边框表示几何模型边界。
5 建模实例及可视化实例
5.1 建模实例
在材料空间中,通过设置控制节点个数决定控制多边形的大致形状,调整p,q的阶数改变B样条曲面的致密程度。由此,提出无函数规则的功能梯度材料建模方法:在材料空间中以自定义方式设计出控制点的位置来获取单一材料的出现范围,再由控制点代入B样条曲面生成算法中,利式(3)生成B样条曲面获得有限个(p×q)矢量节点,并计算获取其节点坐标;将设计好的点梯度源模型中心点放置于节点处,通过叠加原理形成形状规则复杂的材料变化区域,构建材料空间的材料分布结构,然后将材料的分布情况通过组分计算公式的映射函数映射至无材料信息的几何空间上,形成功能梯度材料模型。
③凿槽后使用钢丝刷清刷开凿部位混凝土碎屑,用水清洗干净,在新加结构混凝土浇筑前四小时内刷界面处理剂;界面处理完毕进行植筋,植筋流程如下:植筋定位—钻孔—清孔—注胶—植筋—养护-检测。
举例插入控制点:
b.x=10;b.y=10;b.z=00;b.i=0;b.j=0;
b.x=50;b.y=00;b.z=00;b.i=1;b.j=0;
b.x=90;b.y=10;b.z=00;b.i=2;b.j=0;
b.x=00;b.y=50;b.z=00;b.i=0;b.j=1;
b.x=50;b.y=50;b.z=50;b.i=1;b.j=1;
b.x=95;b.y=50;b.z=00;b.i=2;b.j=1;
b.x=10;b.y=90;b.z=00;b.i=0;b.j=2;
b.x=50;b.y=95;b.z=00;b.i=1;b.j=2;
b.x=90;b.y=90;b.z=00;b.i=2;b.j=2。
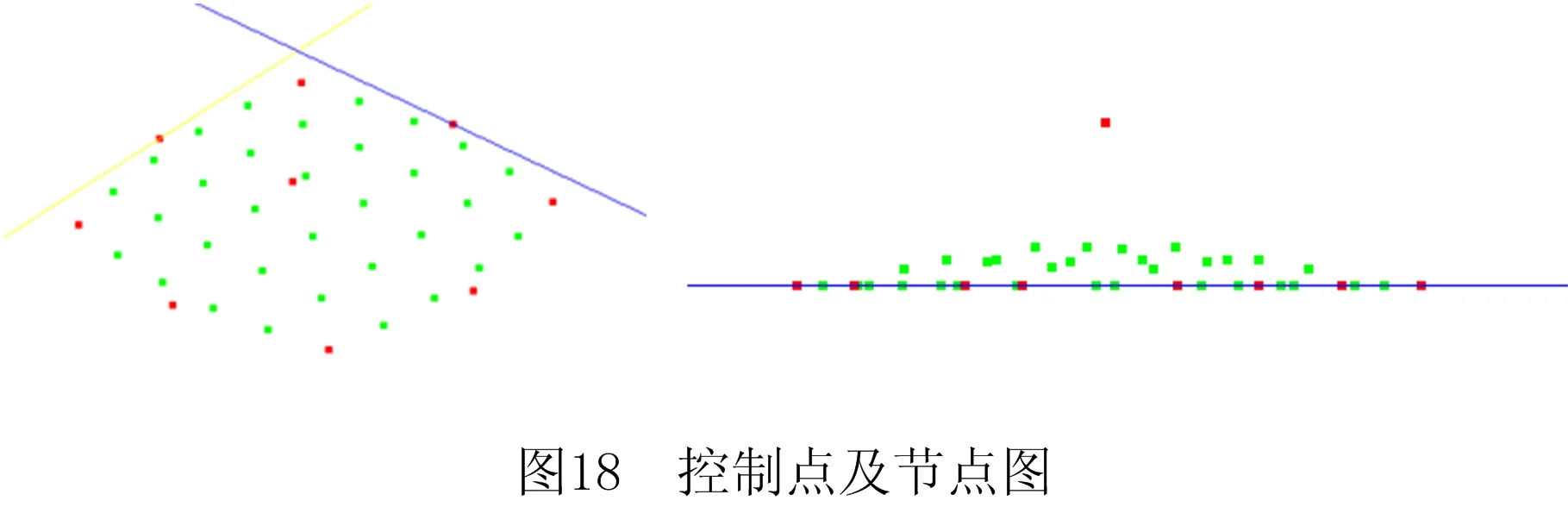
如图18所示,红色点为控制点,绿色点为节点,将梯度源映射在绿色的节点上组成复杂材料模型,生成材料空间结构。图19中生成的蓝色圆为梯度源所映射的区域。

将材料空间中的材料分布结构映射至几何,得到功能梯度材料模型的截面图,通过调整梯度源大小并映射至几何模型上,可以改变材料的分布结构形成新的功能梯材料模型。如图20所示,分别选取映射半径为5mm的梯度源与映射半径为10mm的梯度源,同时作用在100mm×100mm×15mm的立方体上。通过调整梯度源映射半径的大小来改变整体映射效果,形成不同映射区域。

除此以外,还可利用多张B样条曲面,通过保障其连续程度,连结成B样条体,可根据其目标材料的理想分布位置,在其体的内部安置其参数、尺寸、映射规律不同的点梯度源,组合成更加复杂功能梯度材料模型。
5.2 可视化实例
为了证明该建模方法可以简便地、相对容易地设计出结构复杂或仿生结构的功能梯度材料模型,以六种模型结构为例(如图21),并附上梯度源坐标代码。

示例1
b.x=10;b.y=10;b.z=20;b.i=0;b.j=0;
b.x=50;b.y=40;b.z=50;b.i=1;b.j=0;
b.x=60;b.y=10;b.z=20;b.i=2;b.j=0;
b.x=40;b.y=50;b.z=80;b.i=0;b.j=1;
b.x=50;b.y=50;b.z=50;b.i=1;b.j=1;
b.x=60;b.y=50;b.z=80;b.i=2;b.j=1;
b.x=10;b.y=60;b.z=20;b.i=0;b.j=2;
b.x=50;b.y=60;b.z=80;b.i=1;b.j=2;
b.x=60;b.y=60;b.z=20;b.i=2;b.j=2;
示例2
b.x=10;b.y=10;b.z=0;b.i=0;b.j=0;
b.x=50;b.y=10;b.z=0;b.i=1;b.j=0;
b.x=90;b.y=10;b.z=0;b.i=2;b.j=0;
b.x=0;b.y=50;b.z=0;b.i=0;b.j=1;
b.x=50;b.y=50;b.z=50;b.i=1;b.j=1;
b.x=90;b.y=50;b.z=0;b.i=2;b.j=1;
b.x=10;b.y=90;b.z=0;b.i=0;b.j=2;
b.x=50;b.y=90;b.z=0;b.i=1;b.j=2;
b.x=90;b.y=90;b.z=0;b.i=2;b.j=2;
示例3
for (int i=0;i<8;i++)
{
b.i=i;
for(int j=0;j<8;j++)
{
b.x=i*10+j*10;
b.y=i*10+j*10;
b.z=i*10+j*10;
b.j=j;
}
}
示例4
b.x=60;b.y=20;b.z=20;b.i=0;b.j=0;
b.x=60;b.y=60;b.z=20;b.i=1;b.j=0;
b.x=40;b.y=20;b.z=60;b.i=0;b.j=1;
b.x=40;b.y=60;b.z=50;b.i=1;b.j=1;
b.x=20;b.y=20;b.z=0;b.i=0;b.j=2;
b.x=60;b.y=60;b.z=20;b.i=1;b.j=2;
示例5
b.x=80;b.y=0;b.z=0;b.i=0;b.j=0;
b.x=0;b.y=80;b.z=0;b.i=1;b.j=0;
b.x=0;b.y=40;b.z=0;b.i=0;b.j=1;
b.x=0;b.y=0;b.z=80;b.i=0;b.j=2;
b.x=0;b.y=80;b.z=80;b.i=1;b.j=2;
示例6
b.x=80;b.y=0;b.z=40;b.i=0;b.j=0;
b.x=80;b.y=80;b.z=40;b.i=1;b.j=0;
b.x=60;b.y=0;b.z=80;b.i=0;b.j=1;
b.x=60;b.y=80;b.z=80;b.i=1;b.j=1;
b.x=20;b.y=80;b.z=00;b.i=1;b.j=2;
b.x=0;b.y=0;b.z=40;b.i=0;b.j=3;
b.x=0;b.y=80;b.z=10;b.i=1;b.j=3;
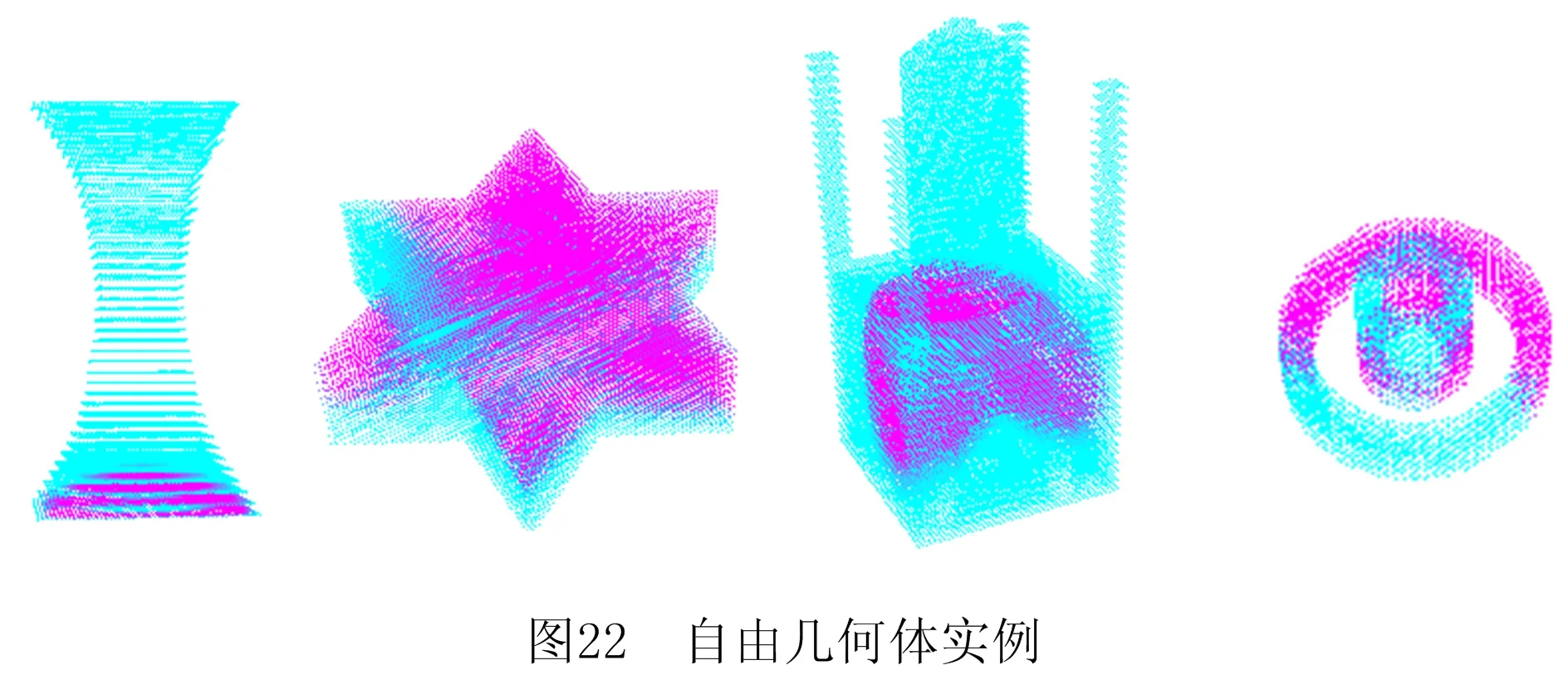
非立方体模型的自由几何体可视化实例如图22所示。
6 实验设备与结果验证
根据本课题组自行设计的微流挤出工艺功能梯度材料3D打印机,采用不同颜色碳酸钙为主的复合水基膏体(牙膏)为材料,通过颜色变化效果直观反映材料分布位置。利用B样条曲面节点与点梯度源结合的建模方法,得到的含有几何信息与材料信息的新型G代码为驱动指令,来验证功能梯度材料的建模与3D打印。
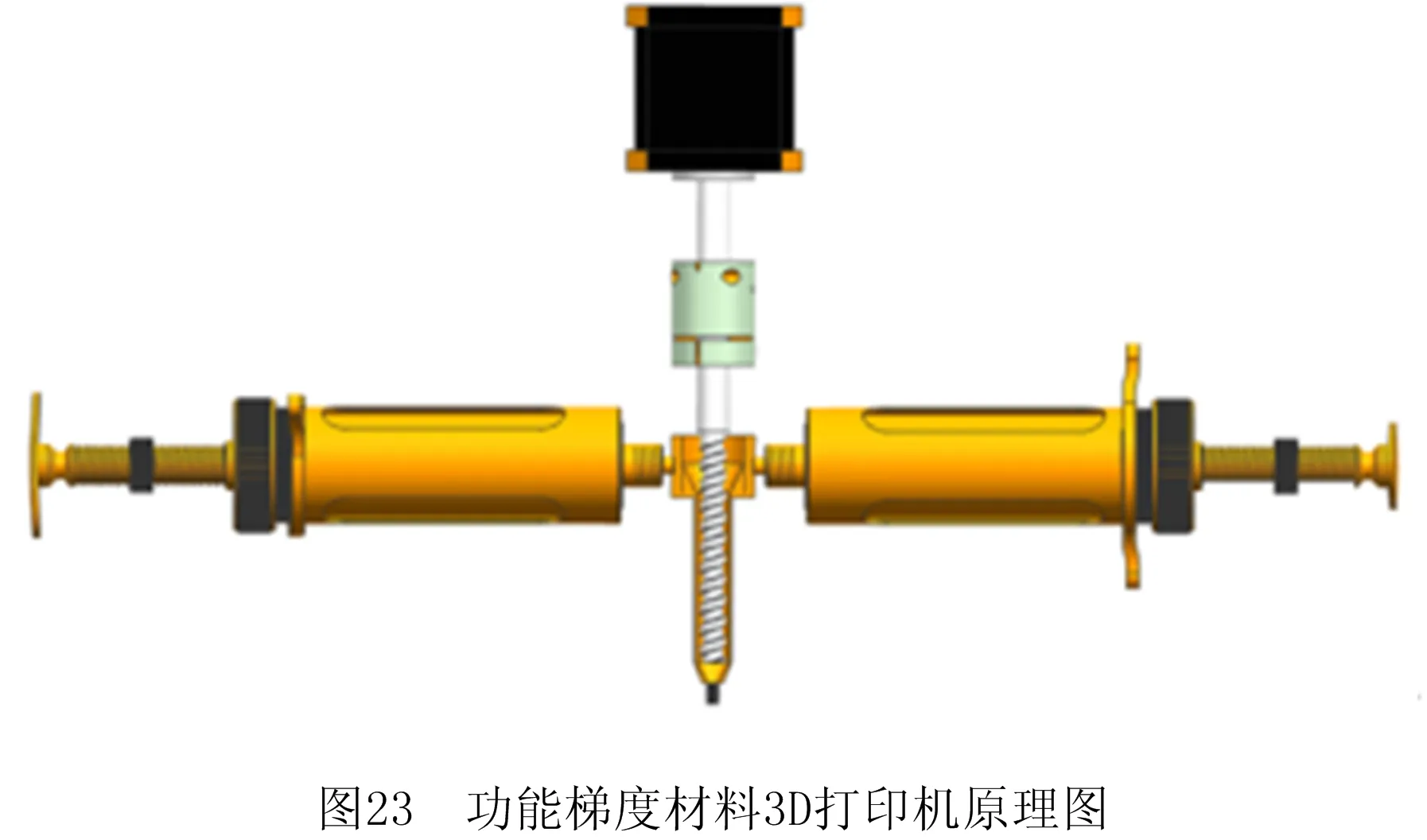
该3D打印机工作原理是采用两种水机膏体作为基础材料,填充在在混料结构两侧由直线电缸推动的两个金属密封注射器。收到驱动控制指令,两电缸根据所需材料的组分不同,按照配比采取不同速度的直线进给,将不同体积的两种材料挤入混料腔中。混料腔由一个步进电机带动变径螺杆,材料受两端的电缸挤压力以及螺杆所产生的剪切力,将材料进行搅拌与加压,使不同比例的两种材料进行充分搅拌,最终将混合完毕的材料由直径0.48 mm的针头挤出。通过两种材料组分实时的动态配比进给,经过混合,可以打印出组分连续变化的挤出丝。微流挤出工艺功能梯度材料3D打印机原理图如图23与打印机样图如图24所示。

为了评估验证功能梯度材料3D打印机系统的工作性能,采用绿色与白色两种膏体作为打印材料,以上文中提及的内外正方体过渡变化作为功能梯度材料模型。通过连续的颜色变化来直观反映其两种材料体积分数之间的动态变化,并通过MATLAB将打印后的模型图片生成灰度图,并标定全白为100%,全绿为0%,按其打印路径顺序进行选点,并生成散点图。
以打印80 mm×80 mm的正方形为例,采用0.48 mm针头,路径间间隔为0.48 mm,路径上分辨率大小设置为1 mm。设白色材料为A材料,则材料A的体积分数随正方形的边缘处到中心处的相关性呈一次递增函数,当打印起始时白色材料体积分数为0%,到达中心处,体积分数上升为100%。由灰度图采集到的数据可知,共采集900个样点,采集方向由绿色材料区域指向白色材料,随着横坐标值的增大,点的数量在增加,同时也表示该点距离打印起始点的距离亦在增加(如图25)。由此经过散点图拟合出的曲线可知,随着点的距离的增加,白色材料的体积分数在呈线性降低(如图26)。

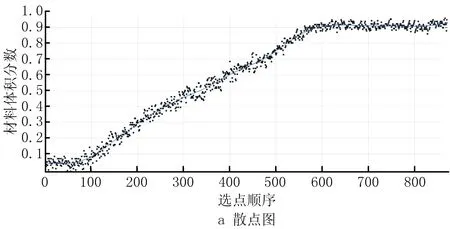
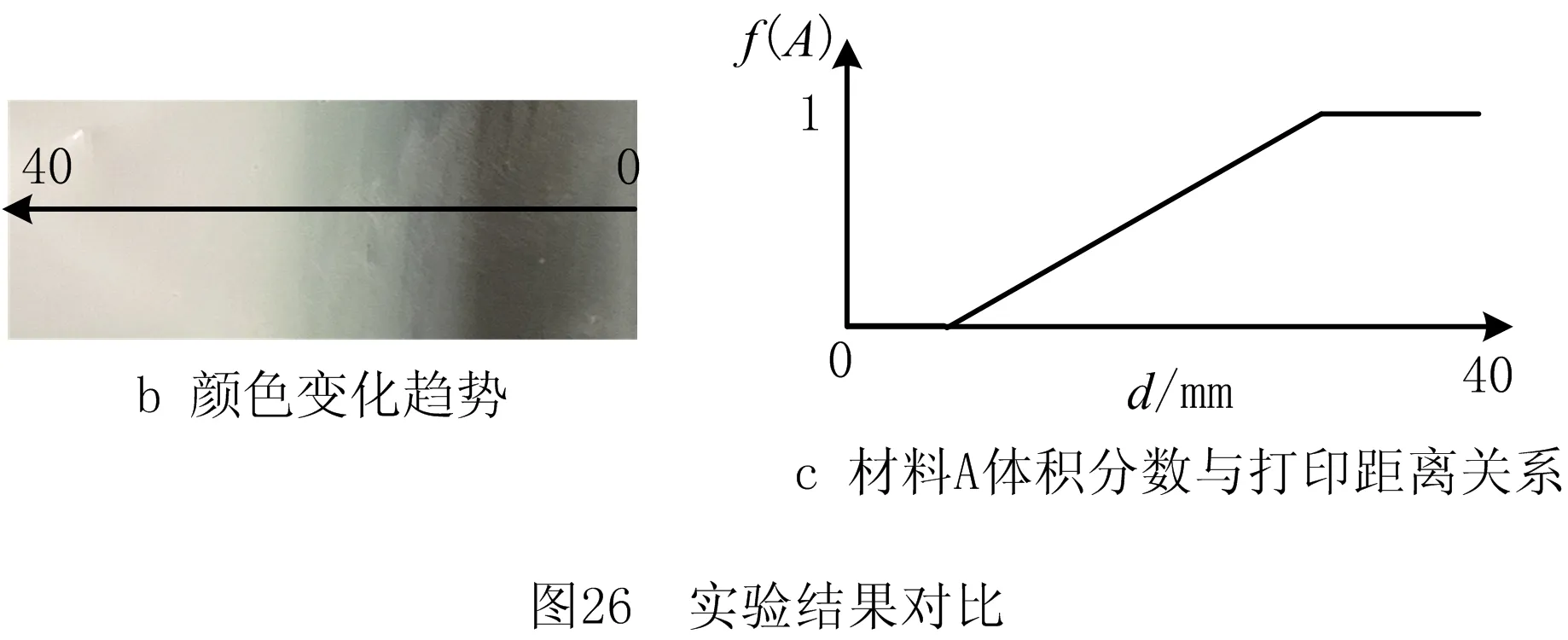
实验节选部分新型G代码如下:
G92 E0
G92 A0
G1 X6.20 Y5.2 E0.0025 A0 F180
G1 X7.20 Y5.2 E0.0050 A0 F180
G1 X8.20 Y5.2 E0.0075 A0 F180
G1 X9.02 Y5.2 E0.0100 A0 F180
G1 X10.2 Y5.2 E0.0125 A0 F180
G1 X11.2 Y5.2 E0.0150 A0 F180
G1 X12.2 Y5.2 E0.0175 A0 F180
其中U与W代表两种不同材料的消耗量累积量。
实验数据结果表明,白色材料的体积分数变化与打印距离的变化关系与预期结果一致,能够遵循目标模型的变化规律。因此,利用B样条曲面节点与点梯度源相结合的建模方法与新型G代码可用于功能梯度材料的3D打印。
7 结束语
本文针对3D打印功能梯度材料的空间映射原理、计算机图形学、信息融合方法,结合材料挤出的打印方式,提出了一种关于复杂材料模型、仿生材料模型的功能梯度材料建模方法,为挤出式3D打印功能梯度材料提供了一条有效途径。通过可视化实例验证了该方法可以通过简单的输入控制点坐标的形式,灵活便捷地创建各类复杂模型,实现对无规则材料模型梯度变化的精准控制。利用该方法,通过打印实验得到了自定义变化的功能梯度材料打印样件,通过实验数据分析证明样件材料梯度变化趋势同理论模型一致,验证了B样条曲面节点与梯度源结合建模方法的正确性、新型G代码合理性、功能梯度材料3D打印机的可行性。但由于混料结构的存在,会出现混料误差,造成打印样件的精准度降低。因此,在未来的研究中需要一种新的路径规划方法,根据材料变化率最小的方向进行打印,降低梯度变化速率,提高打印机混料的准确性,实现更加复杂的材料模型的精准打印。

