遥感卫星快访轨道与机动发射点位一体规划
蔡应洲,贺绍飞,谷振丰,龙 翔,许 晓
(1. 国防科技大学,长沙,410073;2. 酒泉卫星发射中心,酒泉,732750)
0 引 言
“空间快速响应”这一新兴概念,伴随火箭、卫星小型化技术的飞速发展,被不断研究、完善、丰富和发展[1]。空间快速响应具有响应时间短的突出特点,具有极高的民用和军用价值[2]。
快速访问轨道是由Wertz首先提出的一种空间快速响应轨道[3],其能够保证卫星入轨后快速访问目标区域,具有突出的快速响应能力,与空间快速响应任务时效性要求高的特点相契合。但是,Wertz并未给出快速访问轨道的设计方法。目前,作为卫星的典型应用之一,遥感卫星系统无论在民用还是军用领域都具有广泛的应用。因此,研究遥感卫星快速访问轨道具有重要意义。与固定点位发射相比,机动发射不仅可以显著提升生存能力,而且可以大幅拓宽发射窗口,提升快速响应能力,因而成为空间快速响应主流发射方式[4]。付晓峰[5]和贾璐[6]研究了矩形发射区域机动发射快访轨道的设计方法,但相关研究都以轨道响应时间为优化目标,聚焦于轨道设计而不考虑发射点位选取的限制,导致规划得到的机动发射点位均为发射区域顶点,难以适用于实际情况。因此,本文针对公路机动发射,以轨道响应时间和任务响应时间为优化目标,基于目标区域的位置信息和发射区域路网信息,研究遥感卫星快访轨道和发射点位一体规划方法,为空间快速响应轨道和发射点位规划提供理论基础。
1 快访轨道与发射点位规划
1.1 快访轨道设计模型
遥感卫星快访轨道及发射点位一体规划是指在遥感卫星参数、发射区域内路网信息和目标区域位置信息确定的情况下,优化选取机动发射点位,同时设计卫星运行轨道使其入轨首圈即过顶目标区域的过程。目前,主流的快速响应火箭为固体火箭,受固体发动机装药量及装药性能的限制,固体火箭运载能力通常较小,因此,为了保证运载能力,固体火箭通常采用共面发射方式[7],且快访轨道通常设计为近地圆轨道。对于近地圆轨道,其偏心率近似为零,需要设计的轨道参数包括轨道倾角i、升交点赤经Ω和轨道半长轴a,其中升交点赤经Ω由升交点或降交点地理经度决定[8]。此外,对于不同的发射任务,固体火箭的飞行弹道通常不同,为了简化问题,聚焦轨道设计和发射点位规划,假定火箭发射段飞行地心角和飞行时间保持不变。
针对中国周边目标区域的典型空间快速响应任务,假设任务要求以某一技术厂房为依托,应急机动发射某型遥感卫星,在t1时刻观测某一目标区域,提供空间分辨率不大于γm的观测图像,其中遥感卫星性能参数(包括传感器像元间距、光圈数和相机口径)已知。假设O′(λ0, φ0)为技术厂房,C(λ1, φ1)为目标区域,C′(λ′1, φ1)为发射时刻φ1纬度圈与卫星轨道面的交点。假设发射区域(即发射点可选区域)为以O′为中心、半径为L的圆形区域,机动发射点B(λ2, φ2)为位于发射区域内某一路段上的点,K为卫星入轨点,火箭发射时刻空间几何关系见图1。

图1 火箭发射时刻空间几何关系 Fig.1 Spatial Geometry of Rocket Launch
对于近地圆轨道,遥感卫星的空间分辨率为[9]

式中 γ为空间分辨率;h为传感器像元间距;a为轨道半长轴;R为地球半径;d为相机口径;f为传感器光圈数。
由式(1)可知,对于确定的遥感卫星,其空间分辨率仅与轨道高度相关,轨道高度越低,卫星空间分辨率越高。但是,卫星轨道高度越低,卫星对地面目标的持续覆盖时间越短。因此,对于确定的快速响应观测任务(给定空间分辨率要求),通常以空间分辨率上限值确定卫星轨道高度,进而在满足空间分辨率要求的前提下获得最长的持续覆盖时间,即对于确定的快速响应观测任务,卫星轨道半长轴为

式中 γm为快速响应任务给定的空间分辨率上限值。
对于图1中球面直角三角形BDHΔ ,根据正弦定理和余切定理可得

同理,对于球面直角三角形C FHΔ′,可得

对于快访轨道,仅考虑卫星入轨当圈即过顶目标点的情况。假设火箭发射段飞行地心角为θr,则轨道响应时间tp(自卫星入轨至第一次过顶目标点上空的时间)为
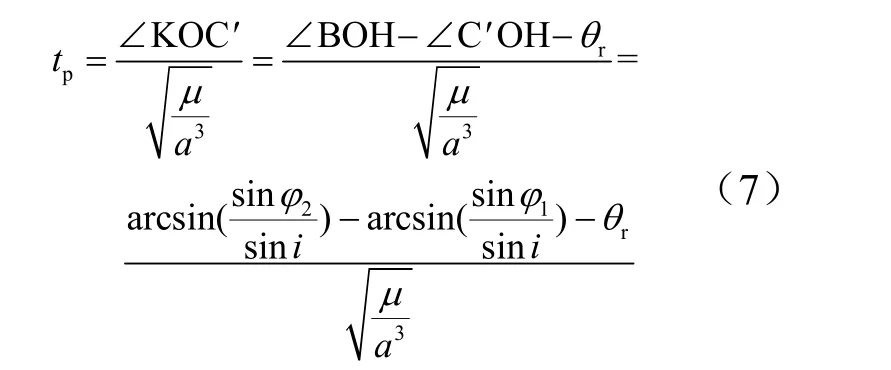
式中 μ为地球引力常数。
对于近地快访轨道,地球非球形引力摄动在所有摄动作用中占据主导地位,其中以J2项摄动的一阶长期项为主。因此,只考虑一阶长期项,可得快访轨道相对地球的运动速率为[10]

式中eω为地球自转角速率。
假设火箭发射段飞行时间为tr,则C′点的经度坐标 1λ′为

式(10)给出了轨道倾角的计算公式。
由图1可知,卫星入轨后第一圈升交点经度φ为
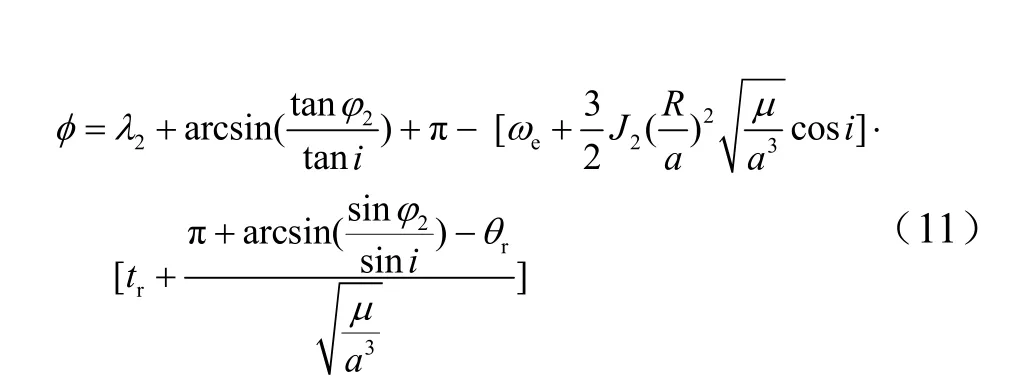
卫星入轨点纬度幅角u为

发射窗口t0为

1.2 发射点位规划模型
针对公路机动发射方式,发射点位的选取依托三级以上公路,将发射区域内三级以上公路划分为直线路段组成的路网,各路段以两端点经纬度表示,以此构建发射区域路网模型(见图2)。
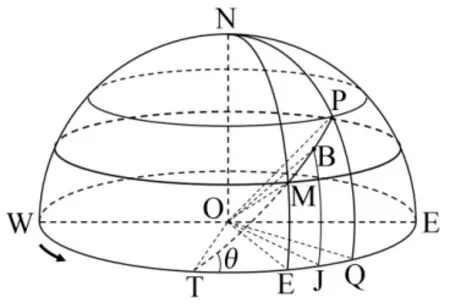
图2 球面路段模型几何关系 Fig.2 Spatial Geometry of Spherical Road Model
假设发射点B (λ2,φ2)位于发射区域某一路段MP上,其中路段MP两端点经纬度分别为 (λM,φM)和(λP,φP),路段倾角为θ(以低纬度路段端点所在维度圈为起始轴,逆时针旋转至路段所转过的角度,θ∈ [ 0,π]),则发射点B经纬度满足以下约束条件:
当θ=0或π时,
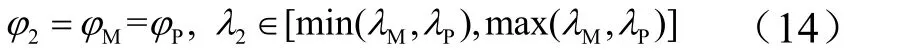
当θ=π/2时,
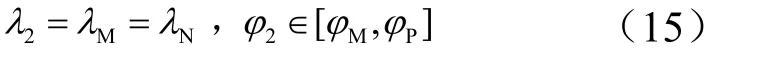
当θ≠0,π/2和π时,
对于球面直角三角形METΔ 、BJTΔ 和PQTΔ ,由余切定理可得

根据λ2- λM=∠ JOT -∠ EOT 可得

其中,θ满足:

1.3 快访轨道及发射点位求解
对于空间快速响应任务,任务响应时间为第一指标,任务响应时间包括火箭载具机动时间、火箭飞行时间和轨道响应时间,计算公式为[11]

式中 tresp为空间快速响应任务响应时间;tj为火箭载具机动时间。

式中 lBO′为机动发射点位与技术厂房之间的最短机动距离;v为火箭载具机动速度。
假设机动发射点位与技术厂房之间的最短机动路径由n条路段组成,则

式中 σr为第r条路段所对应的地心角。

式中 ( λr+1, φr+1)和(λr,φr)为r路段两端点经纬度。
空间快速响应任务要求任务响应时间最短,即火箭载具具有较短的机动时间,同时快访轨道具有较短的响应时间。考虑到机动时间和轨道响应时间均与机动发射点位的选取相关,因此,该问题是以机动发射点位为变量,以任务响应时间为优化目标的单目标优化问题。根据快访轨道设计模型和发射点位规划模型可知,机动发射遥感卫星快访轨道和发射点位规划结果可用x={a, i, λ2, φ2}描述。因此,机动发射遥感卫星快访轨道和发射点位规划问题可描述为

2 具体算例
2.1 任务背景
假设2020年8月18日,强热带风暴在南海某岛屿(117.5°E,15°N)登陆,造成人员伤亡和大量资产受损,考虑到没有合适的遥感卫星近期过顶受灾区域上空,为快速掌握受灾区域受损情况,需要应急发射一颗遥感卫星进行快速响应观测。
2.2 任务需求
2020年8月19日13时(地方时)具备目标岛屿观测能力,空间分辨率不低于1 m。
2.3 初始条件
技术厂房位置O′为东经87°、北纬43°;发射区域半径L=500 km,火箭载具机动速度v=60 km/h;快响火箭飞行参数tr=300 s,θr=30°;遥感卫星参数h=5 μm,d=0.4 m,f=7.5;发射区域内路网信息见表1。
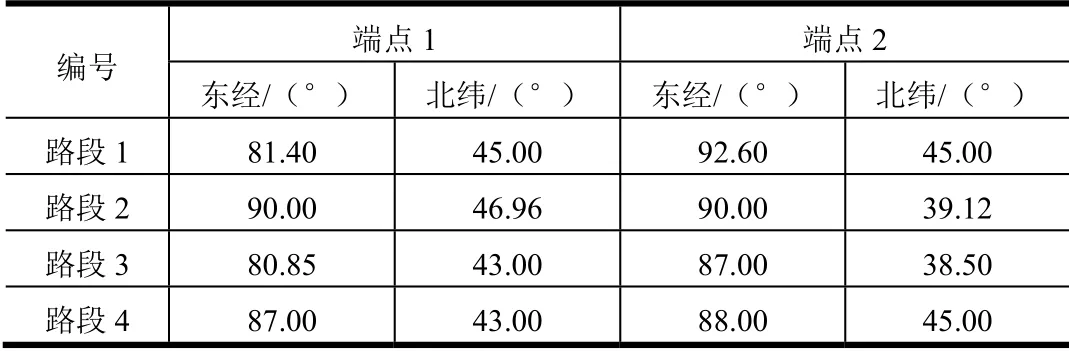
表1 发射区域内路网信息 Tab.1 Information of Roads in Launch Area
2.4 规划结果
由任务需求可知,空间分辨率要求γm=1 m,观测时间要求t1=2020年8月19日6时(世界时)。根据遥感卫星快访轨道和发射点位规划方法,分别以轨道响应时间和任务响应时间为优化目标,得到规划结果见表2。从表中可以看出在发射点(90°E,39.12°N)实施应急发射的轨道响应时间最短(83.25 s),但其任务响应时间相对较长(17.57 h);在技术厂房(87°E,43°N)附近实施应急发射的任务响应时间最短(0.13 h),但其轨道响应时间相对较长(151.97 s)。任务方案的选取取决于任务需求,若任务下达的时间与任务要求完成的时间间隔较短,即任务准备时间较短,则应选取任务响应时间较短的方案,即在技术厂房附近固定发射点位实施发射,但此时装备易暴露,安全性较低;若任务下达的时间与任务要求完成的时间间隔较长,即任务准备时间较充裕,则应选取轨道响应时间较短的方案,即长距离机动发射,此时装备不易暴露,安全性较高,但耗费时间较长。
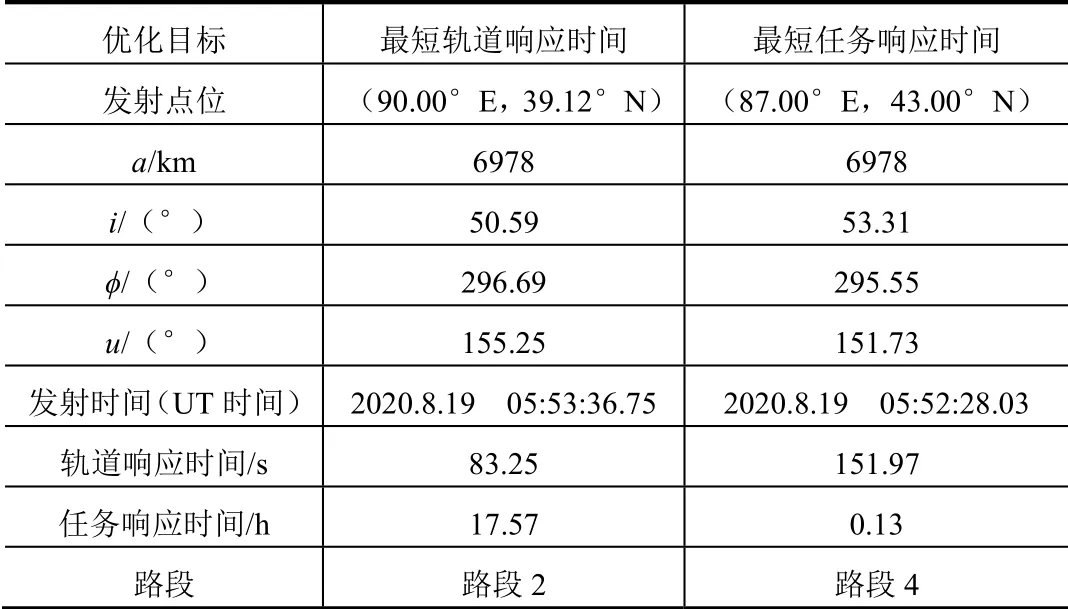
表2 快访轨道及发射点位规划结果 Tab.2 Designed Fast Access Orbit and Launch Position
3 仿真校验
采用STK软件进行仿真校验,设定升交点经度φ′为卫星入轨前一圈升交点经度,计算公式如下:
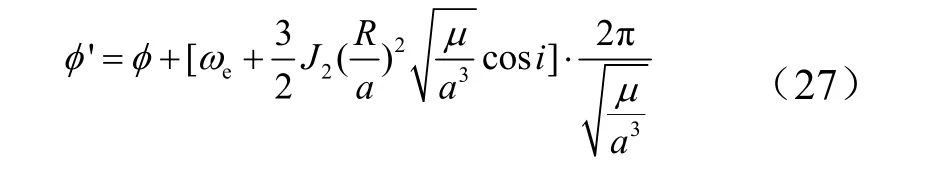
根据式(27)计算得到最短轨道响应时间(tp)min方案和最短任务响应时间(tresp)min方案的升交点经度分别为321.2°、320°。因此,设定(tp)min方案的轨道半长轴、倾角和升交点经度分别为6978 km、50.59°和321.2°,(tresp)min方案的轨道半长轴、倾角和升交点经度分别为6978 km、53.31°和320°,仿真得到的星下点轨迹见图3。

图3 仿真所得星下点轨迹 Fig.3 Simulated Subastral Point Track
从图中可以看出,2个方案卫星入轨首圈即过顶目标岛屿上空,满足空间快速响应需求。另外,从入轨点图中可以看出(tp)min方案卫星入轨点距离目标岛屿更近,表明轨道响应时间更短,与规划结果相符,验证了该规划方法的可行性和实用性。从发射区域图中可以看出(tresp)min方案卫星星下点轨迹经过技术厂房附近,(tp)min方案卫星星下点轨迹经过路段2下端点附近,卫星星下点轨迹并未完全经过规划得到的发射点位,这是由于计算模型中包含火箭发射段飞行弹道,而火箭发射段飞行速度与卫星在轨运行速度不同。
4 结束语
本文基于球面几何知识给出了快访轨道设计模型和发射点位规划模型,进而得到了遥感卫星快访轨道与机动发射点位一体规划方法。所给出的规划方法简单实用,具有一定的工程应用价值。

