以学生为主体的纠错模式研究
江西省赣州中学
廖志勇
1 引言
布鲁纳(J.S.Bruner)在发现学习理论中提出:“学生的认知是在教师循循善诱的引导下,实现自主发现的过程.学生是问题的发现者与解决者,而非被动的接受者.学生通过积极主动的探究与思考,自主发现新的问题,提出解决方案,并获得结论.”由此可见,学生才是课堂的主体,是学习的主人.
错题在日常教学中比比皆是,怎样开发错题资源,鼓励学生自主发现产生错误的原因是高中数学教师必须思考的问题.为了凸显学生的主体地位,让纠错发挥最佳的效果,笔者认为教师可引导学生在纠错的时机、方法与深度上多下功夫,让错题最大化地发挥它的效益.高阶的纠错水平能增强学生的自信,促进各项数学能力的发展.
2 把握纠错时机
学习需要较高的积极性与主动性,纠错亦如此.错题发生后,在学生对题目较熟悉且积极性尚存的时候,教师就应把握好时机,引导学生趁热打铁及时纠错,让纠错成为一种习惯,而不是任务.现实中,有部分教师没有及时批改作业的习惯,学生从完成测试到拿到试卷中间都过了好几天.面对错题,学生已经失去了刚做题时的那股激情,纠错效果自然会大打折扣.
把握纠错的时机,可从以下几方面做起:①教师及时批改作业或测试卷,统计错题数据,做到心中有数.同时,鼓励学生拿到错题及时自主分析错因,尝试依靠自己的能力进行订正.②教师及时有针对性地对典型错误进行引导与拓展,也可充分发挥学生的主体性,采用小组合作的方式,让学生在合作中提高纠错能力.③针对难度较大的错题,教师可设置层层递进的问题引导学生思维,让学生的思维呈阶梯状拾级而上.
此过程,除需遵循及时的原则,教师还要注意学生纠错过程中的思维动态,及时发现存在的共性与个性问题,才能避免类似错误的再次发生.因此,及时督促学生自主订正、检查错题本、有目的性地设置问题、关注学生情感态度等都是促进学生纠错能力提升的关键.
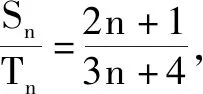
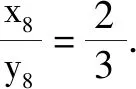
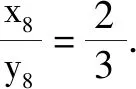
这两种是学生常犯的典型错误,做完本题后,若不及时纠错,学生会坚信自己的方法是正确的,从而将这种错误的方法根深蒂固到自己的认知中.因此,教师应在学生做完题后,带领学生剖析本题,纠正学生错误的解题思路,以优化解题方法.
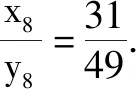
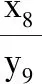
教师把握好纠错时机,在以学生为主体的基础上进行引导与拓展,不仅使得学生自主掌握了等差数列求和的本质,还让学生获得了删繁就简的解题思想.学生在知识的延伸与拓展中有效地促进了应变能力与解题能力的双提升.
3 纠出错误根源
错误的发生绝非偶然,必然会有一个原因.想要在纠错中获得能力的提升,必须在纠错之前挖掘出错误产生的根源.如此,才能在思想上产生深刻印象,从而避免类似问题的再次发生.有些错误原因一目了然,也有些错误的根源比较隐晦,尤其是一些逻辑错误,学生难以自主发现.此时,需要教师适当地引导与点拨,才能达到理想的效果.
凡事都讲究一个方法,纠错也有一定的方法.高中数学错误发生的主要原因有忽视命题的等价性、混淆或误用命题、计算错误等.面对不同类型的错误,学生可根据自己的薄弱点,有针对性地采取不同的纠错方法,而非眉毛胡子一把抓,否则,无法达到因材施教的效果.
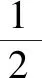

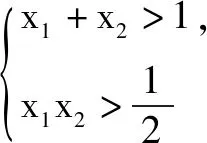
在教师的点拨下,学生恍然大悟,原来自以为简洁、完美的解答过程却犯了逻辑上的错误.只要找到问题的症结点,纠错自然不成问题.因此,纠错的首要因素不是会做题,而是引导学生找出错误发生的原因,对症下药才能达到事半功倍的纠错效果.
4 挖掘纠错深度
皮亚杰(J.Piaget)在他的构建主义理论中也提出:“学生是教学的中心,学习并非是被动接受的过程,而是学生主动参与的过程.”纠错环节,教师在引导学生找出问题的根源后,鼓励学生自主厘清知识的脉络并提出相应的解决办法.如此,更利于学生内化知识,巩固认知结构.
当然,纠错的目的并不在于能解决一道题,而是为解更多、更复杂的问题服务.因此,纠错中,引导学生掌握纠错方法,挖掘知识的纵深是必然的过程.教师可通过层层深入的提问,引导学生的思维跟着问题拾级而上,在知识的拓展与思维的延伸中提升纠错能力.
例3若a1,a2,……,an为等比数列(n≥4),公比q≠1,删掉数列中的一个数之后,得到新数列(顺序不变)为等差数列,求n=4时,正数q的值.
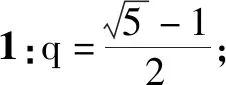
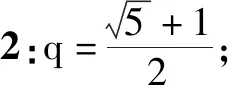

出现这三种错解的主要原因分别是:①只考虑到a1,a2,a4为等比数列;②只考虑到a1,a3,a4为等比数列;③只考虑到第一种情况,同时忽略掉题中的隐含条件(公比为正数).
知道错误发生的原因,纠错就好办了.为了帮助学生达到解一道题会一类题的效果,教师可在学生纠错完成后,进行知识的拓展与延伸,以强化解题思路,拓宽思维,达到触类旁通的效果.
拓展当n=5,6的时候,q值为多少.能满足条件的n(一切可能)值是多少?
此拓展题是对例3解题思想的巩固,同时深化学生对该部分知识点的理解与掌握.当n=5时,a1,a2,a4,a5组成等差数列,唯有a3能删除,则a1+a5=a2+a4,即1+q4=q+q3,进行因式分解得(q-1)2·(q2+q+1)=0.又q2+q+1=0没有实数解,且q≠1,故q=1需舍掉,因此n=5不行.
当n≥6时,不管怎么删,删掉哪项,均会出现原数列中连续的三项,原数列中三项要同时满足等差与等比数列的条件,q必然为1,因此能满足条件的只有n为4.
此拓展题运用了由特殊到一般的数学思想,这是数学学科基本的重要思想之一.学生遇到此类问题,首先应观察题设条件与结论,初步分析题中各个量之间的联系,想方设法将陌生的问题转化成自己认知中所熟悉的问题来思考.
拓展题中思考“满足条件的n(一切可能)值”时,学生可以熟悉的特殊情况“n=4”为思维的起点,遇到不熟悉的特殊情况当“n=5,6”时,可逐个突破,以此来解决一般情况下满足条件的n的可能值.
5 结束语
总之,瞅准纠错时机,精准地找出错误产生的根源是实现纠错能力提升的基础.在此基础上,充分挖掘知识的深度与广度,能有效地激发学生的数学思维,形成良好的纠错方法,从而提高学生的自主纠错能力与数学核心素养.

