数学多选题的审题策略技巧
广东省惠州市惠州中学
陈云韬
一切数学解题的思路、方法、技巧等都来源于认真仔细的审题,而审题是解题的开端之作.著名的数学家、教育家波利亚曾提出“掌握数学意味着善于解题”,将解题过程分为四个基本阶段:审题,转换,实施,反思.其中第一个阶段就是认真审题,要解好题必须先审好题,审题是数学解题的最重要的第一步.审题就是根据题目条件,多角度、多方位分析与观察,由表及里,由内到外,由条件到结论,由数式到图表,洞察问题的实质,找到合适的切入点,选择正确的解题方向.下面结合新高考中多选题这一创新性题型,就多选题的审题策略技巧加以实例剖析.
1 抓住创新定义挖掘审题
在解决一些涉及创新定义(概念、运算、规则、性质等)的多选题中,抓住创新定义的实质,充分挖掘定义中相应的内涵或对应隐含的信息,从创新情境的内涵、实质等层面加以挖掘与分析,有效综合,巧妙类比,正确破解.

A.f(x)=sinx-cosxB.f(x)=lnx-2x
C.f(x)=-x3+2x-1D.f(x)=-xe-x
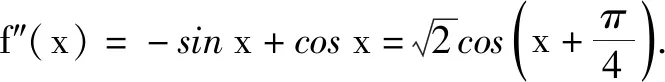
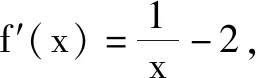
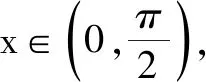
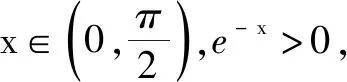
故选:BC.
点评:根据题目条件中给出的创新定义,通过函数的二次求导,结合二阶导函数在给定区间上的取值情况,判断是否恒小于0.也可以通过特例推出矛盾,还可以结合函数图象与性质来分析等.切实抓住创新定义的实质,挖掘内涵,合理审题,巧妙处理.
2 抓住图形特点直观审题
在解决一些涉及函数图象、几何图形、解析几何曲线等多选题中,结合给出的直观图形,观察图形特点,洞悉图形所隐含的特殊关系、数值特点、变化趋势等,数形结合,合理直观审题,巧妙破解.
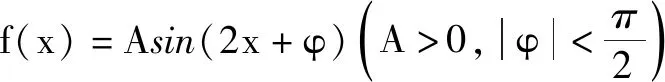

图1
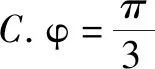
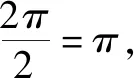

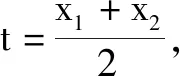
故选:BCD.
点评:根据正弦型函数的图象,通过直观审题,确定三角函数的周期、对称轴、最高点或最低点等,进而确定对应的参数值或函数值.切实抓住图形特点,直观切入加以合理审题,正确推理,巧妙突破.
3 抓住公式结构计算审题
在解决一些涉及数式、公式等结构形式的多选题中,借助对应结构形式,进行分析、加工、转化,联系相关数学知识,链接对应的定义、公式、定理或几何意义等,综合函数性质、方程求解、代数运算等来处理,巧妙计算审题,创新应用,寻找解决问题的突破口.

A.a+b+c=4
B.R=6
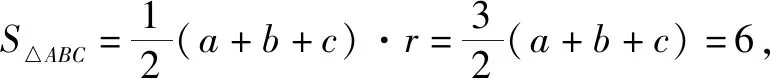
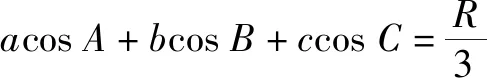
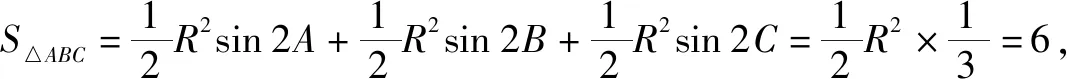
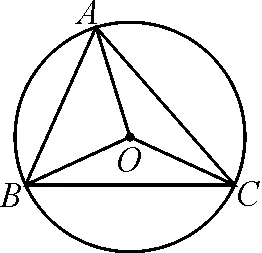
图2
故选:ABD.
点评:根据题目条件中的数式,结合正弦定理、三角形的面积公式等,通过公式的应用与计算加以审题,巧妙突破,判断相关数式的值.切实抓住公式结构特征,联系定义、定理或几何意义等巧妙转化,借助计算加以审题与破解.
数学多选题的审题是解题者对题目条件提供信息的分析、发现、辨认和转译,并对信息作合理有序的提炼与自我转译,是成功解题的必要前提.解题先审题,从宏观上审结论,把握问题的结构特征,总结常见结构的常规处理方式;从微观上抓关键,把握问题的关键点,总结常见的切入技巧与方法.通过复习、学习、练习等不断提升审题能力,养成认真审题、缜密思考的良好习惯,提升解题技巧策略,培养数学核心素养.

