CMA-GFS 4DVar边界层过程线性化的改进

刘永柱 张 林 陈 炯 王 超

1）（中国气象局地球系统数值预报中心，北京 100081）

2）（中国气象科学研究院灾害天气国家重点实验室，北京 100081）

引 言

四维变分同化（four-dimensional variational data assimilation，4DVar）方法的发展和实现是数值天气预报的重大突破之一，是三维变分同化在时间维度上的扩展，暗含了初始背景误差协方差在同化时间窗内的流依赖特征，是一种高效利用高时空分辨率卫星观测资料的成功方法之一［1-3］。目前，4DVar方法已在多个数值预报业务中心得到业务化应用［4-8］。为了满足4DVar业务化所需的计算时效，4DVar一般采用增量变分资料同化技术，在极小化过程中利用时间向前积分的切线性模式（tangent linear model，TLM）和时间向后积分的伴随模式（adjoint model，ADM）计算代价函数的目标泛函和梯度信息［9-10］。TLM 是非线性模式的一阶近似，主要包含两大类线性化模块：动力框架和物理过程。动力框架主要描述大气大尺度演变特征，接近线性，其线性近似精确度较高。物理过程的空间尺度远小于模式动力框架的分辨率，需要采用参数化方法，因此具有强非线性和不连续的特点，如边界层物理过程复杂的湍流运动、湿物理过程强烈的垂直运动和微物理变换等。持续发展和优化线性化物理过程，保持与非线性模式一致是改善4DVar分析和预报效果的有效方法之一［11-13］。线性化物理过程的开发存在很多困难，如需要简化线性化物理过程中的强非线性项，以及解决线性化过程中大量判断语句带来的开关选项不连续问题等［14］，因此在线性化物理过程研发时需要对原物理过程参数化方案进行简化，并对线性化物理过程的相关参数扰动进行规约化处理，确保TLM 和ADM 计算的数值稳定性［11-15］。

近年中国数值预报自主创新发展取得显著进展，建立了以CMA-GFS和CMA-MESO（原GRAPES，Global and Regional Assimilation Pr Ediction system）为核心的数值预报业务体系［2，16-19］。2018年基于CMA-GFS TLM 和ADM 发展的4DVar系统在中国气象局实现业务化［7］，包括增加两个湿线性化物理过程等［12-13］围绕CMA-GFS 4DVar分析预报效果的改善和优化工作持续进行。业务系统的CMA-GFS模式同样在持续发展和升级，其中关于边界层线性化物理过程优化和升级主要内容包括：CMA-GFS模式动力框架在垂直方向上考虑了Charney-Phillips（C-P）跳点的优势［20］，水平风变量分布在模式半层，温度、湿度和水物质变量分布在模式整层，而原边界层物理过程采用的NMRF（新MRF）方案则是基于Lorenz跳点进行计算［21-22］；为了解决边界层物理过程与动力框架垂直格点分布不一致问题，陈 炯 等［23-24］、张 萌 等［25］在CMA-GFS 模式中研发了基于C-P 跳点的NMRF 边界层方案（NMRF_CP），该方案消除了模式预报的边界层温度和湿度不合理的锯齿状振荡，使模式对边界层过程的描述更合理，有效减少了CMA-GFS模式预报误差。

目前，CMA-GFS 4DVar中的边界层线性化物理过程方案采用的是基于Lorenz跳点的MRF 线性化方案（TL_MRF）［26-27］，为了与业务系统CMAGFS非线性模式所采用的NMRF_CP 方案保持一致，并进一步改善4DVar对边界层过程的分析和预报效果，本文研发了基于NMRF_CP方案的新边界层线性化方案（TL_NMRF_CP），并对强非线性特征的平滑和线性化方案的规约化处理进行详细研究。在此基础上，通过试验比较TL_NMRF_CP方案与TL_MRF 方案的切线性近似精度，评估两种方案对4DVar目标泛函相对差异的影响，并利用批量循环分析预报试验检验TL_NMRF_CP 方案在4DVar中的分析和预报效果，为CMA-GFS模式业务化升级提供技术支撑。

1 TL_NMRF_CP方案简介

1.1 NMRF_CP方案

边界层参数化方案是数值预报模式物理过程参数化方案中非常重要的组成部分，它采用平均量描述次网格边界层通量，使大气运动方程闭合并进行求解。目前CMA-GFS模式采用NMRF 边界层方案，该方案考虑一阶K闭合条件，使用K廓线闭合描述不稳定边界层中非局地扩散过程。相较于MRF方案，NMRF 方案主要增加边界层层积云的辐射效应对湍流扩散的加强作用［26］，其方程可表示为

式（1）中，ψ代表模式物理量（如纬向风u、经向风v、位温θ和比湿q），K为热动量扩散系数，γ表示大尺度涡对通量的贡献。

CMA-GFS模式动力框架在垂直方向采用C-P跳点方案，纬向风u和经向风v位于模式半层，位温θ和比湿q位于模式整层。NMRF_CP方案考虑到水平风和温度不在同一垂直层次的特点，采用温度相关量插值到半层计算整层理查逊系数Ri，得到整层热量和动量扩散系数K，通过线性插值得到半层热量扩散系数，可以消除模式预报的边界层温度和湿度不合理的锯齿状振荡，使模式对边界层过程的描述更合理［23-24］。

1.2 TL_NMRF_CP方案

边界层参数化方程（式（1））的切线性方程为

TL_NMRF_CP 方案代码是根据NMRF_CP代码直接编写的，由此得到的切线性方案经常导致TLM 异常增长。为了阻止TLM 的异常增长，本文分别参考ECMWF 边界层方案中阻止异常扰动的方 法［11］和CMA-GFS TLM 针 对MRF 线 性 化 方 案中阻止异常扰动的方法（忽略地表动量通量、热量通量和扩散系数的扰动）［27］。根据TL_NMRF_CP方案在CMA-GFS模式中的具体实现方案，通过试验确认TL_NMRF_CP 方案对切线性量采用的规约化约束处理方法，并与TL_MRF 方案的规约化方法进行对比。TL_NMRF_CP的规约化处理方法比TL_MRF更加精细，TL_MRF 方案中直接忽略了相关变量扰动（如地表热通量和水汽通量扰动，自由大气的理查逊系数Ri的扰动R′i，边界层热量和动量扩散系数的扰动K′，模式最底层的风和温度扰动），TL_NMRF_CP方案中针对这些变量进行更加精细的规约化约束（地表热通量和水汽通量扰动缩小到0.1倍，R′i缩小到0.01 倍，K′和模式最底层风扰动缩小到0.5倍，忽略模式最底层的温度扰动），在确保切线性模式稳定积分的情况下，边界层切线性预报近似取得更好效果。

2 TL_NMRF_CP 方案在CMA-GFS TLM中的评估

2.1 试验设置

本节所采用的模式版本为CMA-GFS 业务化版本（CMA-GFS V3.0），其水平分辨率为1.0°×1.0°，垂直方向为87层，预报时间为6 h，积分步长为600 s。试验初始扰动场采用CMA-GFS 4DVar循环同化系统（CMA-GFS V3.0版本，水平分辨率为0.25°×0.25°，垂直分为87层）提供的分析增量δx（δx＝xa-xb），其中背景场xb是根据三维插值方法将模式6 h预报场由0.25°插值成1.0°，分析场xa是将同化分析场由0.25°插值成1.0°。非线性扰动试验设置为由包含全物理过程的CMA-GFS 非线性模式从两个不同初始条件起报得到的6 h预报场的差值，其中一个以背景场xb起报，另一个以分析场xa起报。切线性扰动试验的模式轨迹是由包含全物理过程的CMA-GFS 非线性模式以背景场xb为初始场计算的。选择不同日期的个例（北半球夏季个例是2019 年6 月1 日，北半球冬季个例是2019年12月1日）测试TL_NMRF_CP 在CMAGFS TLM 中的切线性近似效果，并与TL_MRF方案进行比较。作为参考试验的非线性模式扰动计算采用全物理过程，TLM 扰动试验则采用简化的线性化物理过程，包括次网格尺度地形参数化方案、边界层垂直扩散方案、积云深对流和大尺度凝结［13］。

本节设计两组试验。①TL_MRF试验：基于上文TLM 设置，TLM 的边界层线性化方案采用默认的Lorenz跳点的TL_MRF 方案；②TL_NMRF_CP试验：基于上文TLM 设置，TLM 的边界层线性化方案采用本文研发的C-P跳点的TL_NMRF_CP方案。

2.2 线性化物理过程的诊断方法

本文采用定量方式诊断线性化物理过程对TLM 预报效果的影响。参考试验的非线性扰动预报为两个不同初始条件xa和xb起报的非线性模式预报的差值，即ΔM（δx）＝M（xa）-M（xb），相应需要对比测试的切线性扰动预报为L（δx），M为非线性模式，L为切线性模式。切线性近似效果的诊断方法是比较切线性扰动预报L（δx）与非线性扰动预报ΔM（δx）的绝对误差［11-12］：

ε需要针对每个模式变量在每个模式层和格点上进行计算。绝对误差ε相对于ΔM（δx）的相对误差计算公式为

为了进一步分析不同线性化物理过程对TLM的改善效果，比较两个切线性扰动预报（L2（δx），L1（δx））与非线性扰动预报ΔM（δx）的绝对误差减少量（｜L2（δx）-ΔM（δx）｜-｜L1（δx）-ΔM（δx）｜）的纬向平均分布，如果误差减少量小于0，表示L2（δx）的切线性近似效果好于L1（δx）。

2.3 TL_NMRF_CP方案的切线性近似评估

2.3.1 位温扰动切线性近似评估

根据式（4）计算TL_NMRF_CP 试验和TL_MRF试验全球平均位温扰动相对误差的垂直分布（图1）。由图1可见，对于2019年6月1日个例，相较于TL_MRF试验，TL_NMRF_CP试验在模式9层（约560 m 高度）以下的位温扰动切线性近似预报效果得到有效改善，并且越接近模式低层改善越明显，相对误差最大可减少12%，为了阻止TL_NMRF_CP方案误差的异常增长，对模式底层温度扰动的规约化处理方案导致位温扰动切线性近似在模式9～15 层（大约560～1500 m 高度）略有负效果，这对于TL_NMRF_CP规约化处理方案是可以接受的。对于2019年12月1日个例，TL_NMRF_CP试验在模式14层（约1360 m 高度）以下的位温扰动切线性近似预报效果比TL_MRF 试验更优，TL_NMRF_CP试验对模式低层的改善程度比较接近，相对误差约能减少7%。

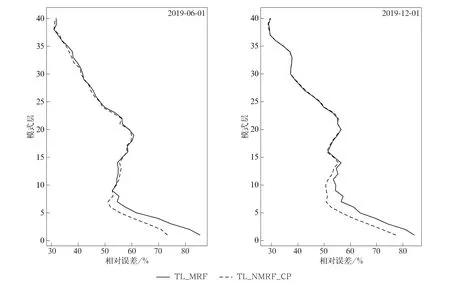
图1 CMA-GFS切线性模式全球平均位温扰动相对误差垂直分布Fig.1 Vertical distribution of global mean relative error of potential temperature perturbation in CMA-GFS tangent linear model

根据式（3）计算TL_MRF 试验纬向平均的位温扰动绝对误差如图2所示，图3是TL_NMRF_CP试验相对于TL_MRF 试验的位温扰动绝对误差减少量的纬向平均。对于2019年6月1日个例，TL_NMRF_CP试验的切线性近似在南极附近改善最为显著（图3），原因之一是TL_MRF试验在此处的位温扰动绝对误差比较大（图2）；TL_NMRF_CP 试验在北半球中高纬度低层也略有改善（图3）。对于2019年12月1 日个例，TL_NMRF_CP 试验切线性近似同样在南极附近改善最为显著（图3），但TL_MRF试验在此处的位温扰动绝对误差（图2）没有2019年6月1日个例（图2）明显；与2019年6月1日个例类似，TL_NMRF_CP 试验在北半球中高纬度低层也略有改善（图3）。总之，基于C-P 跳点开发的TL_NMRF_CP 边界层线性化方案能够有效提高CMA-GFS TLM 边界层位温扰动的预报精度。

图2 TL_MRF试验的位温扰动纬向平均绝对误差Fig.2 Zonal mean absolute errors of potential temperature perturbation for TL_MRF test

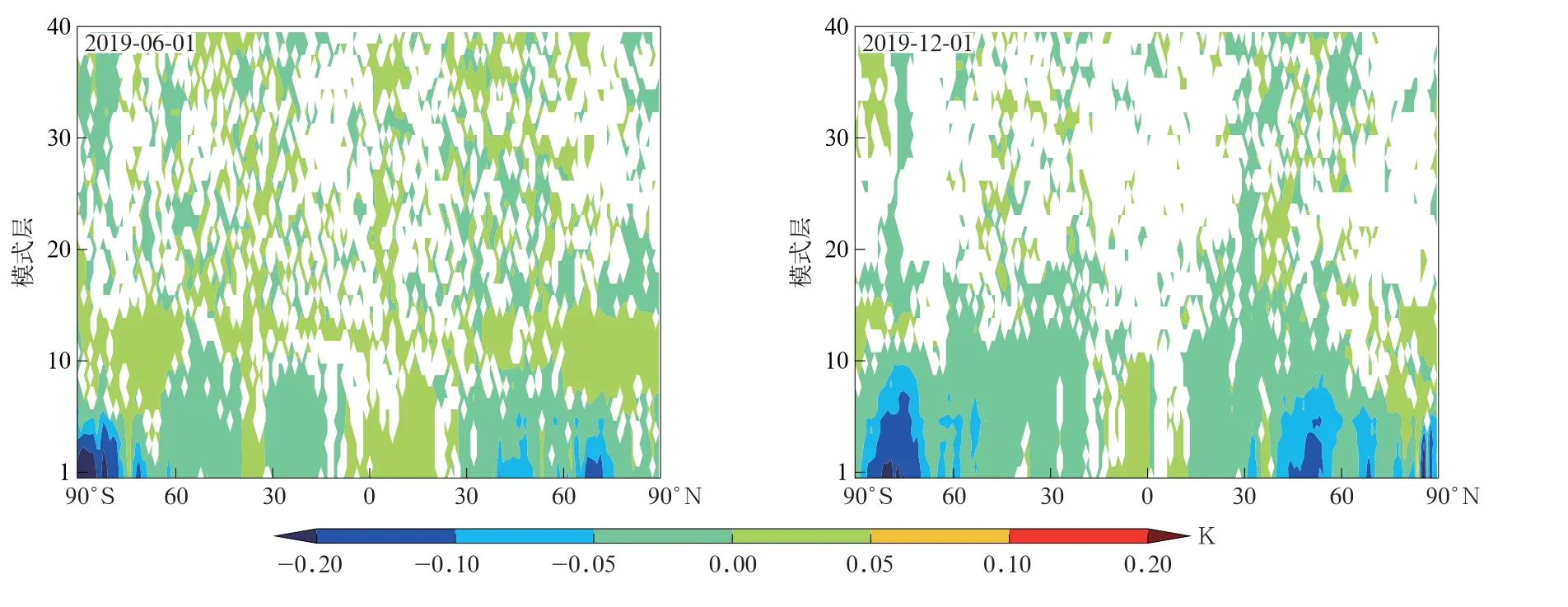
图3 TL_NMRF_CP试验位温扰动相对于TL_MRF试验的改善Fig.3 Improvements in potential temperature perturbation of TL_NMRF_CP test relative to TL_MRF test

2.3.2 比湿扰动切线性近似评估

图4是根据式（4）计算的TL_NMRF_CP试验和TL_MRF试验的全球平均比湿扰动相对误差的垂直分布。由图4 可见，对于2019 年6 月1 日个例，相较于TL_MRF 试 验，TL_NMRF_CP 试 验 在模式28层（约5000 m 高度）以下的比湿扰动切线性近似预报效果得到有效改善，其中模式第5 层（约200 m 高度）的改善最为显著，相对误差可减少约5%；对于2019年12月1日个例，在模式14层（约1360 m 高度）以下，TL_NMRF_CP 试验的比湿扰动切线性近似预报效果较TL_MRF试验好，同样在模式第5层改善最为显著，相对误差可减少约5%。

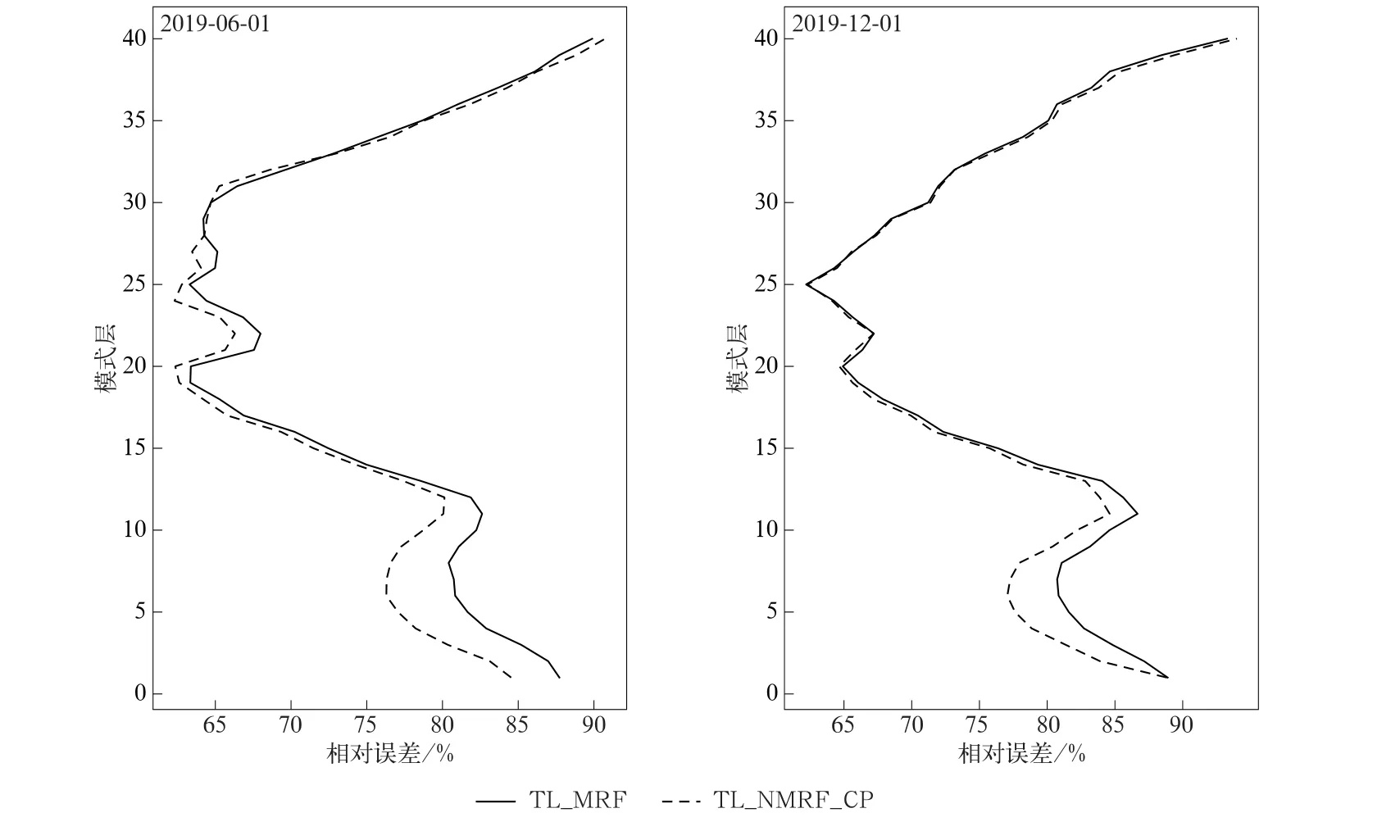
图4 CMA-GFS切线性模式全球平均比湿扰动相对误差垂直分布Fig.4 Vertical distribution of global mean relative error of specific humidity perturbation in CMA-GFS tangent linear model

根据式（3）计算TL_MRF 试验纬向平均的比湿扰动绝对误差如图5所示，图6是TL_NMRF_CP试验相对于TL_MRF 试验比湿扰动绝对误差减少量的纬向平均。由图5和图6可见，对于这两个个例，TL_NMRF_CP 试验切线性近似均在南北半球中低纬度和热带边界层附近改善显著。由此可见，基于C-P跳点开发的TL_NMRF_CP边界层方案能够有效提高CMA-GFS TLM 边界层比湿扰动的预报精度。

图5 TL_MRF试验的比湿扰动纬向平均绝对误差Fig.5 Zonal mean absolute errors of specific humidity perturbation for TL_MRF test

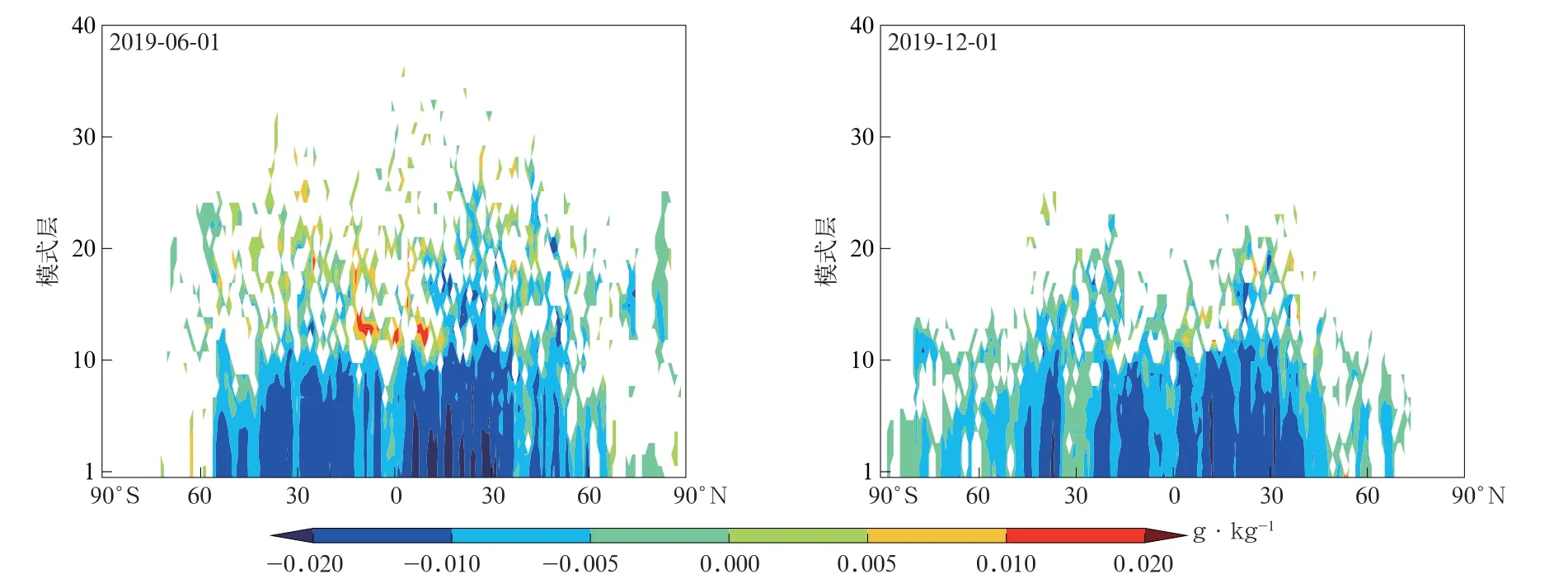
图6 TL_NMRF_CP试验比湿扰动相对于TL_MRF试验的改善Fig.6 Improvements in specific humidity perturbation of TL_NMRF_CP test relative to TL_MRF test

2.3.3 纬向风扰动切线性近似

图7是根据式（4）计算的TL_NMRF_CP试验和TL_MRF试验全球平均纬向风扰动相对误差的垂直分布。由图7可见，相较于TL_MRF试验，TL_NMRF_CP试验纬向风扰动切线性近似在模式低层改善最为明显，相对误差最大可减少约10%。

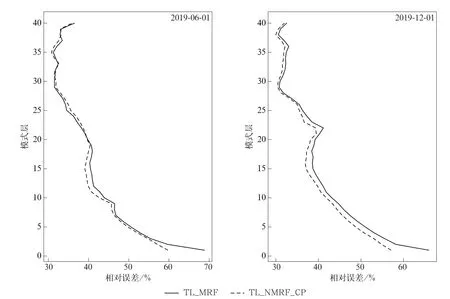
图7 CMA-GFS切线性模式全球平均纬向风扰动相对误差垂直分布Fig.7 Vertical distribution of global mean relative error of zonal wind perturbation in CMA-GFS tangent linear model

根据式（3）计算TL_MRF 试验纬向平均纬向风的扰动绝对误差如图8所示，图9是TL_NMRF_CP试验相对于TL_MRF 试验纬向平均纬向风扰动绝对误差减少量。由图8和图9可见，对于这两个个例，TL_NMRF_CP 试验切线性近似均在南半球高纬度区域（和位温扰动的改善位置一致）以及模式最低层附近有明显改善。由此可见，基于C-P 跳点开发的TL_NMRF_CP方案能够有效提高CMAGFS TLM 边界层纬向风扰动的预报精度。

图8 TL_MRF试验的纬向风扰动纬向平均绝对误差Fig.8 Mean absolute errors of zonal wind perturbation for TL_MRF test

图9 TL_NMRF_CP试验纬向风扰动相对于TL_MRF试验的改善Fig.9 Improvements in zonal wind perturbation of TL_NMRF_CP test relative to TL_MRF test

综上所述，在CMA-GFS TLM 的切线性近似评估中，相较于TL_MRF 方案，基于C-P 跳点开发的TL_NMRF_CP方案可有效改善TLM 对边界层的预报精度，主要原因是基于C-P跳点开发的TL_NMRF_CP 方案与CMA-GFS 非线性模式的边界层物理过程的一致性更高，能更好模拟非线性模式边界层扰动的发展。

3 TL_NMRF_CP方案在CMA-GFS 4DVar中的评估

3.1 评估方法

一般地，4DVar的目标泛函定义为

式（5）中，上标T 表示矩阵转置，上标-1表示矩阵的逆。xa和xb是由模式变量构成的列向量，分别代表分析场和背景场，二者均位于4DVar时间窗的初始时刻。B是背景场的误差协方差矩阵，下标i表示不同时刻，y是观测构成的列向量，M0→i表示从初始时刻t0到观测时刻ti的预报模式积分，H是观测算子，它将模式变量转换成观测相当量，R是观测的误差协方差矩阵。

4DVar通过迭代算法求解目标泛函的极小化问题。由于极小化算法需要目标泛函及其梯度的值，而4DVar的目标泛函和梯度的计算均涉及模式积分，计算量巨大，因此实际应用中通常采用增量分析方案［8］。该方案假定观测算子和预报模式满足线性近似

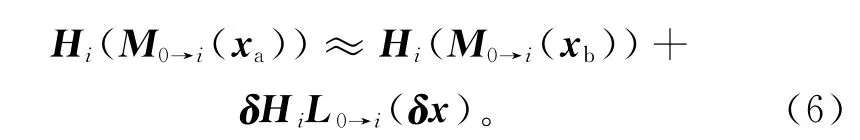
其中，δx＝xa-xb，δHi是观测算子Hi的切线性算子，L0→i是非线性预报模式M0→i对应的切线性模式。此时，目标泛函的控制变量不再是分析场xa，而是分析增量δx，非线性目标泛函J（xa）的极小化问题转化为线性目标泛函J（δx）的极小化问题［7，28］：

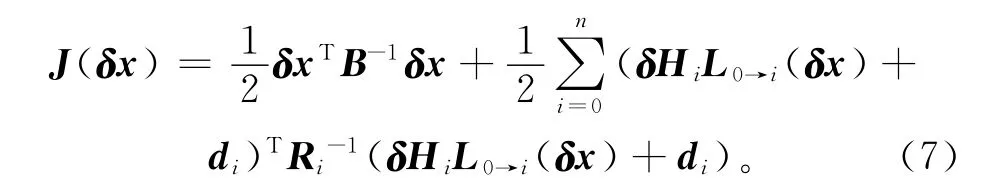
式（7）中，di＝Hi（M0→i（xb））-yi是第i个时刻的观测增量。

显然4DVar目标泛函的式（5）和式（7）的主要差异来自于式（6）的线性近似和4DVar内外循环采用不同分辨率的插值误差。为评估TL_NMRF_CP方案在4DVar的效果，本节计算线性目标泛函J（δx）和非线性目标泛函J（xa）的相对差异

该相对差异反映式（6）中切线性算子δHiL0→i与非线性算子HiM0→i的线性近似程度，相对差异越小，说明两者的近似程度越好。

基于式（7），利用CMA-GFS 4DVar系统同化背景场xb和观测资料得到切线性目标泛函J（δx）的结果和分析场xa；基于式（5），利用分析场xa和观测资料得到非线性目标泛函J（xa）的结果；基于式（8）得到目标泛函的相对差异。

3.2 个例分析

与2.1 节相同，本节也采用CMA-GFS V3.0版 本，选择与2.3节 相 同 的 个 例：2019 年6 月1 日个例和2019年12月1日个例。试验方案如表1所示，采用有预调节的Lanczos-CG 极小化算法迭代50次［28-29］，基于式（8），为更准确地描述TL_NMRF_CP方案和TL_MRF 方案差异，4DVar试验内外循环采用相同的分辨率，以减少4DVar内外循环插值的影响。试验同化的观测资料包括探空观测的温度、风和比湿，地面观测的气压，船舶观测的气压，飞机观测的风，云导风，洋面散射计观测的风以及掩星的折射率。由于TL_NMRF_CP 方案主要影响TLM 模式对边界层的预报效果，未同化卫星资料。本节设计两组试验：控制试验4DVar_MRF，边界层线性化方案采用TL_MRF 方案；对比试验4DVar_NMRF_CP，边界层线性化方案采用TL_NMRF_CP方案。

表1 CMA-GFS 4DVar试验设置Table 1 Setting of CMA-GFS 4DVar test

如图10所示，在迭代次数相同（40次）情况下，两个个例4DVar_NMRF_CP 试验的目标泛函收敛效率均高于4DVar_MRF试验，这说明TL_NMRF_CP方案可以提高4DVar极小化的收敛效率。利用式（8）计算目标泛函相对差异，可以看到TL_NMRF_CP方案可以使2019年6月1日个例4DVar目标泛函的相对差异从7.48%减少到7.01%，2019年12月1 日个例4DVar目标泛函的相对差异由4.71% 减少到3.91%。这说明相较于TL_MRF方案，TL_NMRF_CP方案通过改善CMA-GFS TLM 的预报精度，提高了式（6）的切线性近似，从而降低了CMA-GFS 4DVar目标泛函的相对差异。

图10 CMA-GFS 4DVar目标泛函的收敛Fig.10 Convergence of the cost function under CMA-GFS 4DVar

3.3 批量试验检验

为了检验TL_NMRF_CP 方案在CMA-GFS 4DVar循环同化试验中的预报效果，本节设计两组4DVar循环同化和预报试验：控制试验TL_MRF，边界层线性化方案采用4DVar_MRF 方案；对比试验4DVar_NMRF_CP，边界层线性化方案采用TL_NMRF_CP方案。试验设置如表1所示，积分步长外循环为450 s，内循环为900 s；最大极小化迭代次数为50次；但水平分辨率外循环为0.5°×0.5°，内循环为1.5°×1.5°。循环同化日期为2019年3月1日—2019年4 月30 日，同化所采用资料与CMAGFS 4DVar业务系统一致，包括各类常规和卫星观测资料（探空观测的温度、风和相对湿度，地面观测的气压、船舶观测的气压，飞机观测的风，云导风，洋面散射计观测的风，掩星折射率，NOAA 卫星的辐射率，METOP 卫星的辐射率，风云卫星的辐射率等）［7］。预报试验的起报时刻为12：00（世界时），预报时效为192 h。

经统计，两组4DVar循环同化试验的结果差异很小，此处不详细列出。图11是两组试验基于各自分析场计算的700 hPa位势高度相关系数。为了剔除循环同化试验受到初始时刻（2019年3月1日）背景场调整适应（spin-up）的影响，相关系数预报检验从第11日（2019年3月11日）开始。由图11可以看到，4DVar_NMRF_CP试验的预报评分相关系数在北半球和南半球均高于4DVar_MRF试验。除了700 hPa位势高度相关系数外，4DVar_NMRF_CP试验在其他模式层以及其他评分效果上好于或不逊于4DVar_MRF试验。

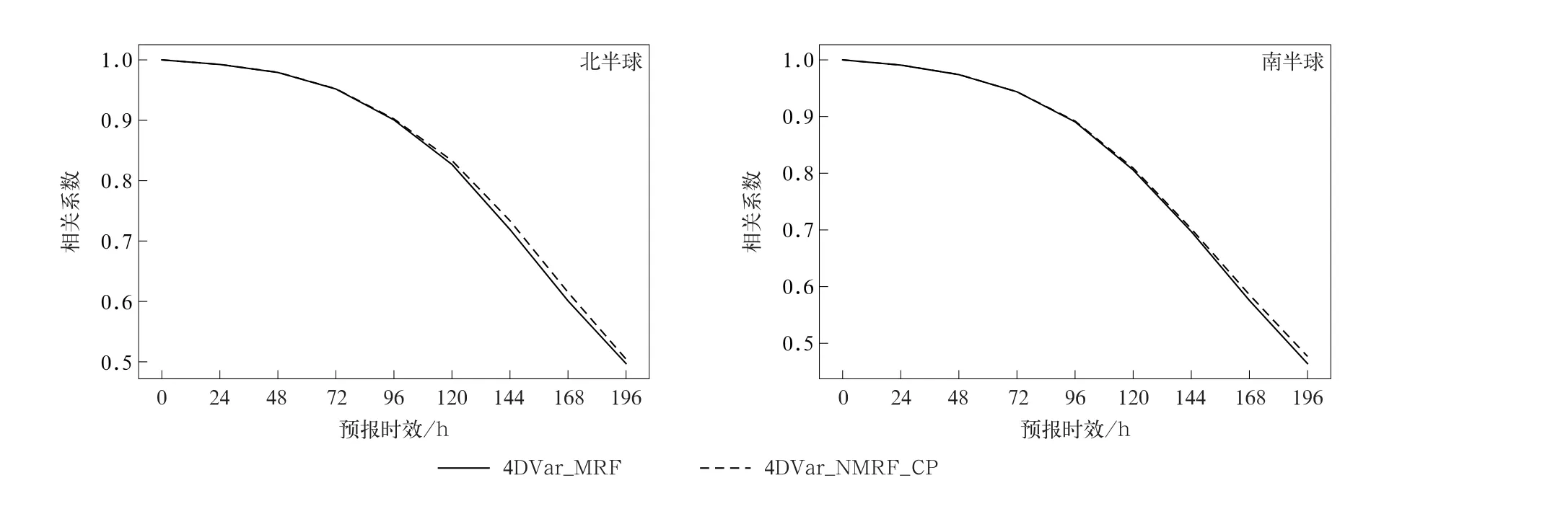
图11 北半球和南半球700 hPa位势高度的相关系数Fig.11 Anomaly correlations of 700 h Pa geopotential height for the Northern Hemisphere and the Southern Hemisphere

4 结 论

为了持续改善CMA-GFS 4DVar业务系统的预报效果，本文研发了基于C-P跳点的NMRF边界层线性化方案，在减少切线性模式扰动异常增长的情况下，为了更好保持边界层线性化切线性方案与非线性方案的一致性，TL_NMRF_CP 方案中针对不同变量扰动采用更加精细的规约化处理方法，得到如下结论：

1）TL_NMRF_CP 方案相对于TL_NMRF 方案可有效改善CMA-GFS 切线性模式中低层位温扰动、比湿扰动和风扰动的切线性预报精度。

2）TL_NMRF_CP 方案可以降低CMA-GFS 4DVar内外循环不同分辨率导致目标泛函的相对差异，提高4DVar的收敛效率。

3）通过CMA-GFS 4DVar循环同化预报试验进一步验证TL_NMRF_CP 方案可提供更好的分析预报效果，目前已经在CMA-GFS 4DVar的业务化系统应用。

CMA-GFS切线性和伴随模式目前在业务上为CMA 全球集合预报系统的奇异向量初值扰动［30］，下一步将TL_NMRF_CP 方案应用于奇异向量计算模块中，改善集合预报初始扰动初值。