一种动态跟踪尺度补偿的ORB特征点提取算法
王传传,周雪云,吴其滨
(广州工商学院工学院,广东 广州 510800)
997459445@qq.com;zhouxy@gzgs.edu.cn;570760876@qq.com
1 引言(Introduction)
SIFT算法和SURF算法无法满足对实时性要求较高的图像处理任务,针对该问题,RUBLEE等[1]提出了ORB(Oriented FAST and Rotated BRIEF)算法,极大地提高了特征点的提取速度。ORB算法是在FAST角点提取算法[2]和BRIEF描述算子的基础上改进得来的,具有旋转不变性,且能抗噪声。ORB算法在速度方面比SIFT算法快两个数量级,比SURF算法快一个数量级,在有些图像数据上的表现更好。
ORB算法的缺点是没有很好地解决尺度不变的问题。换言之,用ORB算法对两幅拥有相同目标物且有尺度差别的图像提取特征点后,匹配点对的数量和质量会因尺度变化而下降。为了解决这一问题,利用带图像金字塔的LK光流算法对跟踪尺度进行补偿,进而优化ORB算法,实现动态跟踪目标物的目的。为了验证该方案的有效性,本文利用OpenCV视觉库进行实验,在算法的运行时间和特征点提取数量方面与原始ORB等算法进行性能对比评估。结果表明,优化后的算法能以较小的时间代价,提高图像特征点的采集数量。
2 ORB特征点检测与描述算法(The algorithm of ORB feature point detection and description)
2.1 O-FAST角点检测算法
FAST(Features from Accelerated Segment Test)特征检测[2]算法认为如果图像中某一像素点与其邻域内多数像素点的属性不同,则该像素点可能为一个特征角点[3]。为了检测某一像素点是否是FAST特征角点,利用布雷森汉姆(Bresenham)直线算法画一个以该像素点为圆心的半径为N个像素单位的圆,FAST算子检测如图1所示。

图1 FAST算子检测Fig.1 FAST operator detection
为了便于辨识,FAST 算法根据N值不同,标记为FAST-N算法。当采用FAST-3时,Bresenham圆共由16 个像素点组成。令点的灰度值为,检测阈值为。若Bresenham圆上的16 个像素点中有连续个点都大于或都小于,则把该点作为FAST特征角点。
上述方法的缺点是必须循环遍历16 个像素点才能做出判断,本文采取了一种加速特征点的获取方法:在16 个点中任意选取一个点作为起始点,沿顺时针方向,每隔90°选取一点,如果这四个点中有三个都大于或都小于,就把此中心点作为FAST特征候选点;反之,此中心点不是FAST特征角点。
经试验证明,当取9时的效果最好,本文采用了FAST-9特征方法,如图2所示。

图2 FAST特征角点Fig.2 FAST feature corner
由于FAST算法不能保持特征点的旋转不变性,所以O-FAST算法在FAST算法的基础上,用强度质心[1]方法添加方向属性,其具体做法如下。
先假设图像中某一区域的质心和几何中心为不同点,利用质心和几何中心所构成的向量刻画方向,则该区域的矩表示如下:

2.2 R-BRIEF特征点描述算法
针对基于梯度直方图的特征描述符,SIFT和SURF算法无法满足对实时性要求很高的系统,Michael Calonder等人提出了一种基于BRIEF算子[4]的特征描述算法,其实现步骤如下。
Step1:进行定义测试。
在高斯平滑处理后的图像上选取一块大小为S×S的局部区域,在区域上进行测试:


选取BRIEF-64[4]进行介绍,即BRIEF特征串的存储空间占64 个字节,共需64×8=512 bits。
Step2:进行点对的选择。
由公式(5)可知,构建一个512 bits的特征串需要512 个有序点对。
由于BRIEF算法不具备旋转不变性,所以需要将BRIEF改造成具有旋转感知性(Rotation-Aware)的R-BRIEF算法。ORB算法采用BRIEF-32,即描述符的串长度为256 bits。本文选取了组测试点对,组成一个的矩阵:


所以,受控的BRIEF算子(steered BRIEF)可定义如下:
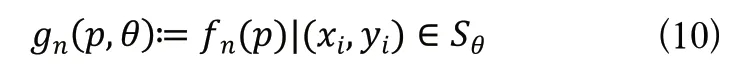
为了加速计算过程,预先构建一张查找表,将角度离散化,步进单位设为,只要离散化的O-FAST特征角点方向与上述角度标尺相符,则可以通过查找表查找对应的点集,并计算描述符。
BRIEF描述符采用点对的方式进行测试,这种方法虽然简单易行,但是无法较好地抑制噪声。为了解决这一问题,ORB算法采用点集对的方法。如图3所示,以特征角点为中心选取一个边长为的正方形邻域,在该邻域中用边长为的正方形子窗口(点集)代替BRIEF描述符中的点,用点集对代替BRIEF描述符中的点对。这样该邻域中应有个子窗口。从中任取两个构成点集对,那么点集对的数量为,去掉窗口相互覆盖的点集对,真正可用的点集对的数量为。
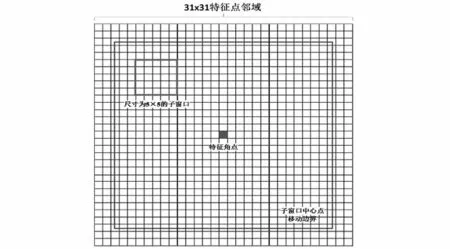
图3 R-BRIEF测试集Fig.3 R-BRIEF test sets
未添加旋转特性的BRIEF具有的一个优点是二进制特征描述符有较大的方差且均值在0.5附近,可以很好地对特征点进行区分;而添加旋转特性的steered BRIEF却丧失了这一特性。本文采用高斯BRIEF点对100 k个样本特征点进行描述,得到均向量的位响应均值分布。同时,ORB算法通过如下操作提高steered BRIEF的辨识度。
(2)将测试结果按照与0.5做差,得到的值按从大到小排序,得到队列T。
(3)应用贪婪算法:①将队列T的队首移入结果集R中;②队列T的新队首与结果集R中的所有结果进行比较,若它们的相关性大于预设阈值,则放弃队首,减少结果集R的冗余信息,否则添加到R中;③当结果集R有256 个元素时,将R作为描述符,若R中的元素个数不及256 个,则提高预设阈值,然后重复前两个步骤。
3 ORB算法的改进(Improved ORB algorithm)
3.1 光流动态跟踪法
运动物体在视频中表现为相关目标特征像素点在连续帧的移动,而由于人眼的视觉暂留现象,因此像素点的移动可以用“光流”刻画,用光流的矢量速度对图像中物体的运动信息进行描述。带图像金字塔的LK(Lucas-Kanade)光流算法[5]可以解决多尺度下“大运动”的跟踪问题[6]。原始的LK算法(假设条件如图4所示)的实现必须具备下面三个假定条件[7]。

图4 LK算法的条件Fig.4 Condition of the LK algorithm
条件1:灰度保持不变。
视频中运动的目标物在相邻帧间的灰度保持不变,则

也就是说,运动目标物的灰度不随时间的变化而发生改变,那么:

条件2:“小运动”。
运动目标物体在连续帧间的位移较小,即属于“小运动”。由公式(11)、公式(12)和链式法则,可得到:

实际场景中,不能完全保证满足前两个假定条件,导致计算的光流速度会有微小的偏差。因此,只要按照上述方法求得的光流速度足够接近真实的速度,就可以利用牛顿法迭代得到相对准确的收敛解。如图5所示,将首次获得的有偏差的光流速度作为初始值并进行下一次迭代,之后重复该过程。依据第一假定条件可知,空域导数始终保持不变,而时域导数每次迭代前都要重新计算,正常经过5 次迭代收敛即可获得满意的光流速。

图5 牛顿法求光流速度的收敛解Fig.5 Convergence solution of optical flow velocity by Newton method

如图6所示,由于已知条件少,导致无法求出二维空间下的光流速度,只能获取垂直运动分量,这也被称作孔径问题[7]。通过小孔,观察不到物体的下移运动,只能观察到物体的右向运动,如图7所示。

图6 二维光流速度的求解Fig.6 Solution of two dimensional optical flow velocity

图7 孔径问题Fig.7 The aperture problem
为了解决孔径问题,就需要用到第三个假设条件。
条件3:运动区域的空间连续性。
在运动场中,由于目标物在图像中的投影是区域性的,表现为连续帧之间位移的像素点,其邻域的像素点也具有类似的位移趋势。本文通过建立中心点邻域像素的方程组增加约束条件,从而避免了孔径问题的出现。如果采用5×5的邻域描述中心点的运动状态,则

当两条或两条以上的边缘出现在5×5的窗口邻域中,可利用最小二乘法求解该系统方程。通过公式(17)求解得残差平方和的最小值:

实际场景中,视频获取到的动态目标相对于图像尺度来说位移较大,导致LK算法处理跟踪问题所得的结果也不理想。当用大尺度窗口跟踪“大运动”时,又会破坏第三条运动连贯性的假设条件。本文引入图像金字塔模型,采用由粗至精的方式(Coarse-to-Fine)对光流进行估计,金字塔顶层的一个像素点可以表征其最底层的若干个像素点,从金字塔最顶层对光流进行估计,并将估算的结果作为下一层估计的初始值。这不仅避免了“小运动”的约束限制,而且随着计算的向下进行,计算精度也会提高[8]。算法演示过程如图8所示。
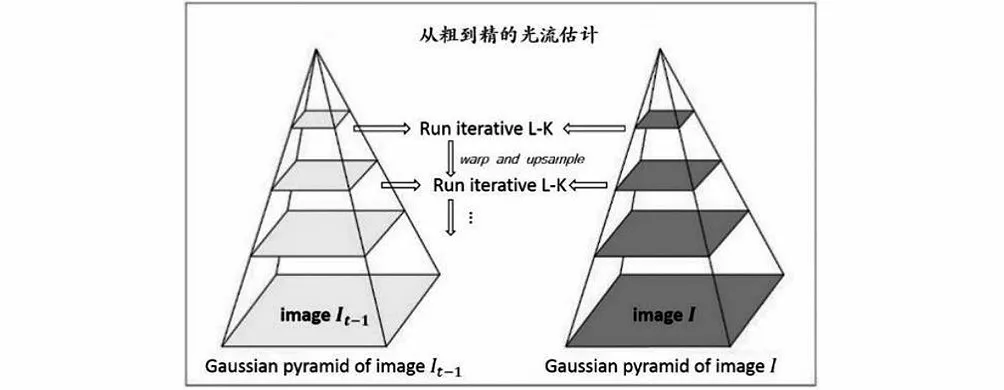
图8 带图像金字塔的LK光流算法Fig.8 LK optical flow algorithm with image pyramid
3.2 基于动态跟踪的尺度补偿策略
由于ORB算法中的O-FAST角点检测和R-BRIEF特征描述都没有解决尺度问题,也就是说ORB算法不具备尺度不变性,在全景拼接的过程中,场景的尺度通常不会发生剧烈的变化,为了避免视图场景中(比如在高速公路上行驶的汽车)突发的极端情况,对尺度不变性的保证还是必要的,而且这么做可以很好地提高拼接的准确度和精确性。
本文利用带图像金字塔的LK光流算法对跟踪尺度进行补偿[9-10],并进行实验。视频中产生的尺度变化是由目标物与背景产生消逝点方向的相对运动导致,如图9所示。静止场景往往不会发生尺度变化,当目标物的尺度发生变化时,ORB算法所检测到的特征点数可能会下降,当添加运动跟踪算法后,目标物可以最大限度地保留原始的特征点,这样就保证了ORB算法检测的特征点不因尺度变化而丢失。如图10(a)中,汽车的部分特征信息因尺度变化而丢失,图10(b)中,带图像金字塔的LK算法对ORB进行补偿,保留了上一帧中汽车的部分特征信息。

图9 消逝点方向相对运动产生尺度上的变化Fig.9 Scale changes produced by the relative movement of the vanishing point

图10 光流法对ORB算法的尺度补偿Fig.10 Scale compensation of ORB algorithm by optical flow method
本文通过带图像金字塔的LK光流算法对视频中的物品进行动态跟踪实验。在视频的同一帧,分别利用原始ORB算法和经尺度补偿后的ORB算法提取特征点,对比采集结果,如图11所示。

图11 特征点提取对比实验Fig.11 Comparative experiment of feature point extraction
从图11(a)和(b)可以看出,图片尺度上有明显的差异,从A、B区域提取的特征点密集程度可以看出,经尺度补偿后的ORB算法提取的特征点数量要明显多于原始ORB算法。
此外,通过摄像头采集视频数据,选择采集视频前30 帧的数据,运用OpenCV视觉库进行实验,对尺度补偿后的ORB算法的运行时间和特征提取数量进行对比统计,结果详见表1。
表1 特征提取算法性能对比Tab.1 The performance comparison of feature extraction algorithms
由表1可知,原始的ORB算法比SIFT算法快两个数量级,比SURF算法快一个数量级。经动态跟踪尺度补偿后的ORB算法和SURF算法的时间损耗基本相当,但补偿后的ORB算法提取的特征点数量约是SIFT算法的2.44 倍、SURF算法的2.24 倍、原始ORB算法的1.47 倍。结果表明,经动态跟踪尺度补偿后的ORB算法性能更优。
4 结论(Conclusion)
本文介绍了ORB算法的特征提取和特征描述算法,指出ORB算法不具有尺度不变性。在全景拼接中,为了确保图像匹配的准确性,需要对原始的ORB算法进行改进。由于带图像金字塔的LK光流算法,可以解决多尺度下“大运动”的跟踪问题,即该算法对“大运动”、多尺度下的动态跟踪有着良好的效果。基于此,本文运用动态跟踪的方法对ORB算法进行尺度补偿,分析了该设计思路的可行性。为了验证动态尺度补偿后的ORB算法性能,在Windows系统下,通过摄像头采集视频数据,利用OpenCV视觉库进行实验,在算法的运行时间和特征点提取数量上与原始ORB等算法进行对比,结果表明:经过动态尺度补偿后的算法能以较短的时间代价,提高特征点的采集数量,实验结果符合预期,为提高图像特征点提取性能提供了一种理论支持。

