非对称×形折叠翼巡飞弹气动特性数值研究
邱佳伟,陈少松,徐一航,魏 恺,吕代龙
(南京理工大学 能源与动力工程学院,江苏 南京 210094)
巡飞弹作为无人机与弹药技术有机结合的信息化武器,不仅能够对敌实施精确、有效的打击,还能够承担战场侦察监视、战斗毁伤评估、通信以及无线电中继等单一或多项任务,必将成为弹药发展的重要趋势。受设计任务、起飞场地和发射装置的影响,巡飞弹的气动布局形态各异,目前巡飞弹的气动布局主要有串列折叠双翼布局、前掠折叠翼布局、固定翼布局、多旋翼布局、怀抱式展开翼布局、一字形展开翼布局等[1-4]。
为了缩小弹箭的横向尺寸,便于运输和发射、节省导弹的储运空间,巡飞弹多采用折叠翼和折叠舵。由于折叠方式的不同,气动布局也有所不同,巡飞弹主要分为轴对称气动布局和面对称气动布局。而本文所研究的非对称×形折叠翼巡飞弹(如图1所示)为非面对称气动布局。与传统的折叠方式有所不同,该种气动布局的舵翼并不是沿着弹身轴线进行折叠,而是从与弹身相切的位置进行折叠(如图2所示),具有大展弦比的特征,可获得较大的升阻比。

图1 非对称×形折叠翼巡飞弹示意图Fig.1 The diagram of patrol missile with asymmetric X-folded fin

图2 ×形折叠翼折叠示意图Fig.2 Diagram of asymmetric X-folded fin
这种折叠方式可以增大弹身内部使用空间,减少弹身内部设计的复杂程度,且便于携带、使用方便,可以为步兵提供精确的视线监视和攻击能力。Uvision公司所研制的Hero-30巡飞弹就是采用该气动布局,Hero-30巡飞弹可以在几分钟内完成部署,具有30 min续航时间,飞行距离可达40 km,可以打击轻型装甲车辆、快艇和步兵等移动目标[5-8]。
目前,国内外关于非面对称巡飞弹气动布局的研究较少,其气动特性随马赫数、攻角变化规律尚不明确。因此本文采用数值模拟的方法对×形折叠翼巡飞弹的气动特性进行研究。
1 计算模型与计算方法
1.1 计算模型
本文所研究的计算模型如图3所示,左侧为对称模型(symmetric model,SM),右侧为非对称模型(asymmetric model,AM)。两者的弹径、弹长、翼与舵的弦长和暴露展长均相等,翼型采用NACA0012翼型。最大弹径D为140 mm,全弹长L为8.71D。参考长度为全弹长L,参考面积S=(πD)2/4,力矩参考点为弹头,坐标为(0,0,0),参考坐标系取弹体系。远场静压为101 325 Pa,静温为288.15 K。计算域边界参考弹箭长度,亚音速前场取12.5L,后场取25L,周场取140D[9-11]。

图3 模型示意图Fig.3 Diagram of models
1.2 网格划分
网格的划分对于后期的计算结果影响较大。计算网格可分为结构网格和非结构网格,而非结构网格又可以细分为两种:一种是全流域为非结构网格,一种是边界层采用非结构网格,其它采用非结构网格,即混合网格。本文所研究的×折叠翼巡飞弹由于外形特殊,舵翼与弹身的连接处结构相当复杂。因此本文采取非结构网格中的混合网格进行划分。如图4所示,网格划分采取的是多面体-六面体核心网格,即主流域采用笛卡尔网格,在近壁面采用多面体网格。

图4 模型网格示意图Fig.4 Grids and cells of the model
1.3 控制方程与计算方法
本文控制方程采用三维积分形式的雷诺平均N-S方程[12]:
(1)
式中:t为时间,S为面积,V为任意控制体,W为守恒变量,F为无粘通矢量项,FV为粘性通量,∂V为控制体边界,n为控制体边界单位外法向矢量,Re为雷诺数。
空间离散采用二阶迎风格式,对流分量应用Roe通量差分分裂,时间推进格式采用隐式时间推进格式。湍流模型选择k-ωSST模型。
1.4 网格无关性验证
本文对于SM模型和AM模型分别划分了三套网格:SM模型的网格数量分别为320万、430万和530万;AM模型的网格数量分别为340万、450万和560万。选择验证的计算工况为:Ma=0.6,α=6°,以便进行网格数量收敛性验证。计算结果如表1和表2所示,其中N代表网格数量,|ε|为相对误差值,Cn为法向力系数,Cz侧向力系数。SM模型的相对误差值是由320万、530万网格数量的计算结果分别于430万网格数量的计算结果相比得到的,AM模型的相对误差值是由340万、560万网格数量的计算结果分别于450万网格数量的计算结果相比得到的。

表1 SM模型网格独立性验证Table 1 Cell independence verification of SM model

表2 AM模型网格独立性验证Table 2 Cell independence verification of SM model
SM模型的网格验证如表1所示,当网格数由320万增加到430万,法向力系数Cn误差为5.12%,但当网格数增加到530万,与430万的结果相比,误差仅为0.45%,所以对于SM模型本文选取430万这一套网格为后续计算。
AM模型的网格验证如表2所示,当网格数由340万增加到450万,法向力系数Cn误差为3.44%,侧向力系数的误差为6.25%,但当网格数增加到560万,与450w的结果相比,法向力系数Cn与侧向力系数Cz的误差为0.11%和0.68%,误差均在1%以内,侧向力系数的误差之所以偏大,这是由于侧向力的值较小。所以对于SM模型本文选取450万这一套网格为后续计算。
2 计算结果
针对对称模型(SM)与非对称模型(AM)分析马赫数和攻角对升力系数CL、阻力系数CD、侧向力系数Cz与滚转力矩系数Cmx的影响。
2.1 侧向力系数随攻角和马赫数的变化规率
图5为SM模型与AM模型在不同马赫数下侧向力系数随攻角的变化曲线。由图可知,两种模型侧向力系数的大小有所不同。

图5 侧向力系数随马赫数和攻角的变化规律Fig.5 Variation of lateral force coefficient with Mach number and angle of attack
对于SM模型,侧向力系数最大为0.017,而AM模型的最大值为-0.49(负号代表方向)。因此,与AM模型的偏航力矩系数相比,SM模型侧向力系数的值几乎为0。对于AM模型,侧向力系数随着攻角的增大,呈现先增大后减小,再增大的趋势。
2.2 滚转力矩系数随攻角和马赫数的变化规律
图6为SM模型与AM模型在不同马赫数下滚转力矩系数随攻角的变化曲线。与AM模型相比,SM模型的滚转力矩系数几乎为0;而AM模型在0~6°攻角内,不同马赫数下滚转力矩系数为正,且值是逐渐减小的;在8~10°攻角内,不同马赫数下滚转力矩系数为负,且值(绝对值)逐渐增大。当Ma=0.4,α=2°时,其滚转力矩系数的最大值为0.011 95。

图6 滚转力矩系数随马赫数和攻角的变化规律Fig.6 Variation of rolling moment coefficients with Mach number and angle of attack
2.3 升力系数随攻角和马赫数的变化规律
图7为SM模型与AM模型在不同马赫数下升力系数随攻角的变化曲线。SM模型与AM模型的升力系数随着攻角的增大而线性增大,符合升力系数的气动规律;升力系数在同一攻角下随着马赫数的增大,升力系数也略有增大,且随着攻角的增大,升力系数增大的越明显。SM模型与AM模型的升力系数随着攻角和马赫数的变化趋势大致相同,由于两者的暴露展长保持一致,所以升力系数的差值不大。从整体上来看,SM模型的升力系数略大于AM模型。

图7 升力系数随马赫数和攻角的变化规律Fig.7 Variation of lift coefficients with Mach number and angle of attack
2.4 阻力系数随攻角和马赫数的变化规律
图8为SM模型与AM模型在不同马赫数下阻力系数随攻角的变化曲线。随着攻角的增大,弹箭的迎风面积增大,因此阻力系数也相应增大。在Ma=0.4~0.5时,阻力系数相差不是很大,当Ma≥0.6,阻力系数增大得比较明显;从整体上来看,SM模型的阻力系数略小于AM模型。
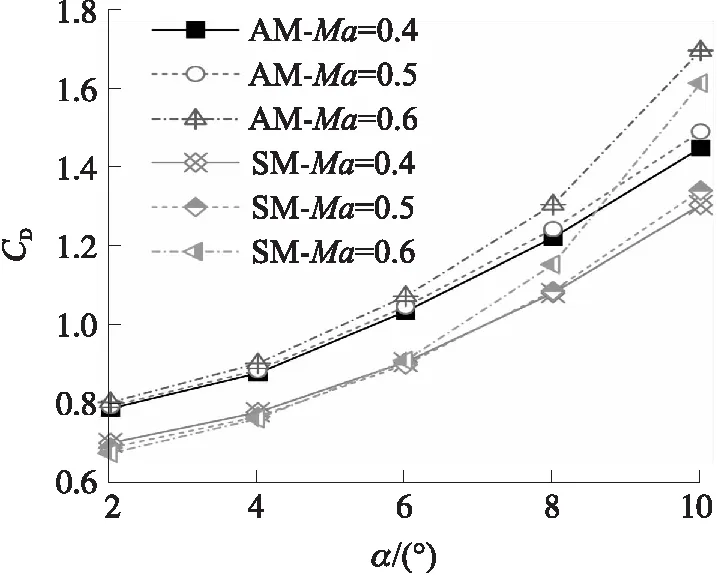
图8 阻力系数随马赫数和攻角的变化规律Fig.8 Variation of drag coefficients with Mach number and angle of attack
3 SM模型与AM模型气动参数比较分析
SM模型与AM模型在气动参数上存在差异,主要是由模型上的改变造成的,但是这是采用折叠翼和折叠舵所必须付出的气动代价。而折叠方式的不同所带来的结果是气动布局上由对称变为非面对称。非对称的气动布局必然会导致非对称的气动参数,如侧向力系数与滚转力矩系数,因此需对AM模型与SM模型的气动差异进行比较分析[13,14]。
3.1 侧向力系数分析比较
如图5所示,SM模型的侧向力系数可以忽略。对于AM模型而言,主翼在总的气动参数上起着很大的作用。在主翼前的流场,由于未受到翼身干扰的影响,流场应是对称分布,而对于主翼后的流场,由于受到了翼身干扰的影响,流场应为非对称分布。而侧向力正是由翼身干扰引起的,为了验证这一点,本文在弹身X=0.3 m与X=1.0 m处分别取剖面1与剖面2(如图9所示),用以观察主翼前的流场与主翼后的流场的分布情况。
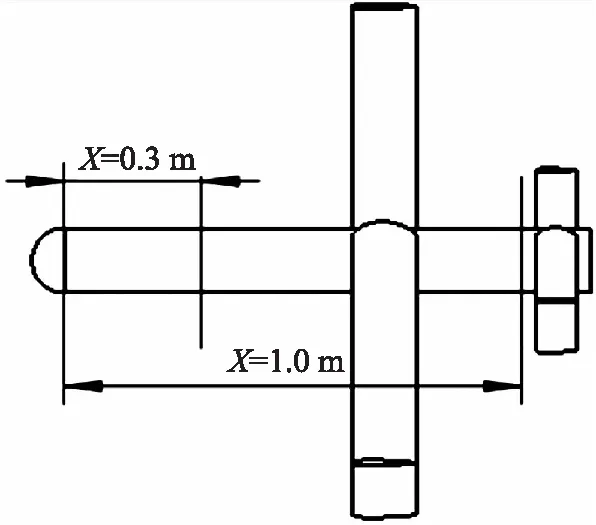
图9 弹身的剖面位置Fig.9 Sectional position of patrol missile body
图10为Ma=0.6,α=10°时,剖面1与剖面2两个平面的压力云图与流线分布情况。在X=0.3 m处,由于流场未受到翼的干扰,所以在这个平面上的流线与压力云图分布是对称的;但X=1.0 m处,受到了翼的干扰,这个平面上的流线和压力云图呈现非对称分布的规律。

图10 Ma=0.6,α=10°时,流线与压力分布情况Fig.10 Flow line and pressure distribution when Ma=0.6 and α=10°
为了进一步说明翼前流场和翼后流场的变化规律,给出了剖面1与剖面2处弹身表面压力的分布随着攻角的变化情况,如图11所示。在剖面1处,随着攻角的增大,压力也随之改变,压力总体上是对称分布的。

图11 Ma=0.6,弹身压力分布随攻角变化情况Fig.11 Variation of missile body pressure distribution with angle of attack when Ma=0.6
但是在剖面2处,压力呈非对称分布,且随着攻角的增大,这种非对称情况就越来越明显,在10°攻角的情况下尤为突出。所以剖面1处的压力分布情况与流线分布情况是吻合的,均为对称分布,而剖面2处的压力分布与流线分布是非对称的。(注:0°到180° 为弹身上半部分,180°到360°为弹身下半部分)
通过上述对两处剖面的压力、流线与弹身压力分布的分析,可以确定AM模型的翼身干扰是非对称的,但是并不能确定侧向力的产生是由翼身干扰的非对称性造成的,因此需要分别对AM模型的弹身与舵翼的侧向力进行分析。图12给出了AM模型弹身与舵翼的侧向力系数随攻角的变化规律。对于单个主翼来说,侧向力系数较大,但是翼1与翼3的侧向力系数与翼2与翼4的侧向力系数的符号相反,代表侧向力的方向是相反的,因此四个主翼的侧向力系数可以相互抵消一部分的,且侧向力系数的大小随着攻角的增大而增大;舵的侧向力系数的分布和变化规律与翼的大致相同,唯一的区别就是舵的侧向力系数较小。

图12 Ma=0.4时,AM模型弹身、翼和舵的侧向力系数随攻角的变化规律Fig.12 Variation of lateral force coefficient of body,fin and canard of AM model with angle of attack when Ma=0.4
以6°攻角为例,四个主翼的侧向力系数的代数和为0.359,四个尾舵的侧向力系数的代数和为0.092,两者的和为0.451。但是由图5可知,在马赫数为0.4、攻角为6°的状态下,侧向力系数为负,这是由于主翼对弹身的干扰使得弹身也产生了侧向力。由图12可知,弹身的侧向力系数为负,与舵翼总的侧向力系数相反,且绝对值大于舵翼总的侧向力系数,所以总的侧向力系数是负的,为-0.133,与弹总的侧向力系数是相符的。由此可得,侧向力是由翼身干扰的非对称性引起的。
3.2 滚转力矩系数分析比较
如图6所示,SM模型的滚转力矩系数为零,而AM模型存在滚转力矩系数。图13给出了AM模型弹身与舵翼的滚转力矩系数随攻角的变化规律。由图可知,弹身的滚转力矩系数为零,因此弹身并不存在滚转力矩;对于舵,虽然随着攻角的增大,滚转力矩系数也随之增大,但最大绝对值仅为0.037,而舵1与舵4的值为正,舵2与舵3的值为负,因此与侧向力一样也可以相互抵消,四个舵的最大代数和为0.007;四个主翼的滚转力矩系数的分布情况与四个尾舵一致,翼1与翼4的值为正,翼2与翼3的值为负,四个翼的最大代数和为0.017 539。因此总的滚转力矩系数为正。

图13 Ma=0.4时AM模型弹身、翼和舵的滚转力矩系数随攻角的变化规律Fig.13 Variation of rolling moment coefficient of body,fin and canard of AM model with angle of attack when Ma=0.4
3.3 升力系数分析比较
由前文可知,AM模型和SM模型的升力系数在不同马赫数与攻角下的变化趋势大致相同。本节将分成三个部分,分别从弹身、翼、舵三个方面进行分析。
3.3.1 弹身的升力系数分析
由前文分析可知,AM模型受翼身干扰,气动参数与SM模型有所区别,升力系数也有所不同。图14给出了SM模型与AM模型在Ma=0.4时,弹身的升力系数随着攻角的变化规律:AM模型与SM模型弹身的升力系数均是随着攻角的增大而增大,但是AM模型的升力系数总是小于SM模型,且随着攻角的增大,两者的差值越来越大,这是由于主翼和弹身之间产生的干扰,使得翼的洗流洗到弹身上,降低了AM模型的弹身升力,且随着攻角的增大,AM模型受到的影响越大。

图14 弹身的升力系数比较Fig.14 Comparison of lift coefficient of patrol missile body
3.3.2 翼的升力系数分析
由于SM模型的四个翼,沿弹身是对称分布的,所以SM模型四翼的升力系数应该相等的。
对于AM模型而言,由于翼沿着弹身的分布是非对称的,所以四个翼受到弹身的干扰不是完全相同,从而四个翼的法向力系数也不是完全相同。图15(a)给出了SM模型与AM模型翼1和翼2升力系数随攻角的变化规律。由图可知:SM模型与AM模型的翼1和翼2升力系数差别很小,这是由于AM模型的翼1与翼2处于弹身的上半部分,受到的干扰比较小,且暴露展长相同。图15(b)为SM模型与AM模型翼3和翼4升力系数随着攻角的变化规律。由图可知:SM模型的翼3与翼4升力系数相同;AM模型的翼3的升力系数小于SM模型的翼3,而AM模型的翼4的升力系数大于SM模型的翼4。之所以会出现这种情况,是因为翼3与翼4位于弹身的下半部分,且由于两者并不是面对称布置的,所以受到的干扰不相同,所造成的结果就是两者的升力系数不相同。图16为Ma=0.4,α=8°时AM模型的翼的压力云图。由图可知,翼4下翼面的总体压力要高于翼3下翼面的,因此翼4的升力系数要大于翼3的,这与上述分析相符。

图15 翼的升力系数比较Fig.15 Comparison of lift coefficient of fins

图16 Ma=0.4,α=8°时AM模型的翼的压力云图Fig.16 Pressure contour of fin of AM model when Ma=0.4 and α=8°
3.3.3 舵的升力系数分析
对于SM模型,舵的变化规律应与翼的变化规律一致,由图17可知,舵1与舵2、舵3与舵4的升力系数的值是一样的。对于AM模型而言,舵位于翼的后方,因此不仅会受弹身的影响,也会受到翼的影响,因此洗流对舵的影响比较复杂。
图17(a)给出了SM模型与AM模型舵1和舵2升力系数随攻角的变化规律,图17(b)给出了SM模型与AM模型舵3和舵4升力系数随攻角的变化规律,由图可知:由于受到翼身干扰的影响,使得AM模型的舵1与舵2的升力系数均大于SM模型的;AM模型的舵3的升力系数却小于SM模型,而AM模型的舵4的升力系数却大于SM模型,这是由于AM模型的舵3与舵4受到的干扰不同,从而造成两者附近的压力分布的差异。图18给出了Ma=0.4,α=10°时AM模型的舵的压力云图(左侧为舵4,右侧为舵3),在舵4下舵面的压力要高于舵3下舵面的压力,因此舵4的升力系数要大于舵3的,这与计算的结果也是符合的。

图17 舵的升力系数比较Fig.17 Comparison of lift coefficient of canards

图18 Ma=0.4,α=10°时AM模型的舵的压力云图Fig.18 Pressure contour of canard of AM model when Ma=0.4 and α=10°
3.4 阻力系数分析比较
图19给出了SM模型和AM模型的正视图,SM模型是常规的×字布局,而AM模型采用折叠翼和折叠舵,由于舵翼并不是沿着弹身轴线进行折叠,而是从与弹身相切的位置,因此在保证弹长,弹径、暴露展长等几何特征相同的情况下,AM模型的迎风面积要略大于SM模型,而阻力系数的大小随着迎风面积的增大而增大,因此AM模型的阻力系数要略大于SM模型,这与阻力系数的计算结果也是相符的。

图19 SM模型与AM模型正视图Fig.19 Front view of SM model and AM model
4 结论
本文通过数值模拟方法,对巡飞弹非对称×形折叠翼气动特性进行仿真分析,将计算结果与×形翼气动布局进行比较,比较了二者的气动差异,得到以下结论:
①在亚音速下,SM模型的侧向力系数与滚转力矩系数为零,而AM模型的侧向力系数与滚转力矩系数不为零。
②在亚音速下,AM模型的侧向力系数随着攻角的增大呈现先增大后减小再增大的趋势;随着马赫数的增大而增大。
③在亚音速下,AM模型的滚转力矩系数在0到6°攻角内,滚转力矩系数为正,且值是逐渐减小的,在8到10°攻角内,滚转力矩系数为负,且值(绝对值)逐渐增大。
④与SM模型相比,AM模型的阻力系数略大于SM模型,升力系数略小于SM模型。

