箔条干扰弹动态抛撒云团空间分布研究
陈 昊,孙雪明,刘建功,阮文俊
(1.南京理工大学 能源与动力工程学院,江苏 南京 210094;2.江西星火军工工业有限公司,江西 南昌 331709;3.河北太行机械工业有限公司,河北 石家庄 052160)
箔条能在一定的空间范围产生干扰回波[1],使得雷达无法准确识别出目标而达不到预期攻击效果[2]。研究箔条云从产生到扩散过程中的形态大小和取向分布等性质,对探究其电磁散射特性的变化极为重要[3]。
ALVAREZ等[4]提出了一种用于一般箔条云电磁模拟的离散箔条云模型,可以用来计算谐波或宽带脉冲散射响应。该技术考虑了箔条云的几何形状和箔条在密度和方向上的统计分布。SEO等[5]运用六自由度扩散模型得到了低雷诺数下箔条位置和取向随时间的变化情况。杨学斌等[6]在忽略箔条质量的前提下建立了箔条云团的布朗运动扩散模型。李志辉等[7,8]应用随机动力学加权技术及概率统计分布原理对箔条云整体性能进行了分析。曾涛等[9]基于对箔条云边界处若干高速箔条位置的计算提出了一种箔条云整体运动模型。TONG等[10]为了实现箔条快速散开提出将一种高速旋转的飞行器作为箔条投放器。
现有的研究为模拟箔条云飞行覆盖范围及整体运动性能提供了方法,但存在以下不足:①部分学者提出的模型只适用于成熟箔条云的研究[6],无法对处于发展过程中的箔条云及其性能进行分析;②箔条云模型大多由球形发展至椭球型[7-11],与实战过程中箔条云形态发展的有一定差距;③随着近年来反箔条干扰工作的进展[12,13],仅研究云团的宏观外形发展已不再能满足有效干扰的需求,云团内部箔条如何分布已成为高成功率干扰的关键。
鉴于以上问题,本文运用刚体动力学理论和碰撞概率模型,在单根箔条运动模型的基础上,研究具有高牵连速度的箔条集群动态抛撒后的多体分离过程,得到箔条云团轴向截面由锥形发展至矩形的分布模型,并与试验结果对比,验证计算模型的准确性和有效性,在此基础上分析处于扩散阶段及沉降阶段云团内部箔条的分布规律。为后续研究不同牵连速度下箔条的动态抛撒提供参考。
1 计算模型
1.1 刚体动力学及运动模型
由于在模拟箔条抛撒的计算空间范围内箔条所占体积比例远低于气相场,箔条对气相场的作用可以忽略不计,因而本文只考虑气相场对固相的作用,而忽略固相场对气相场的反作用。
为避免过大的计算量,本文以一定量的取样箔条群代替数目庞大的真实箔条群,通过跟踪计算每一个箔条求解离散场。计算时将每一个箔条离散成若干等份的箔条小段,对箔条小段进行受力分析,将箔条小段受力合成求得箔条所受合力,并求得箔条所受力矩;根据箔条所受合力及力矩,求其在计算空间范围内的运动。
如图1所示,Oxyz为固定参考坐标系的平移坐标系,Oξηζ为体坐标系。描述箔条姿态的3个角为进动角ψ、章动角θ、自转角φ。上述3个角即称为欧拉角,在一定的条件下,刚体的任一方位可用一组欧拉角唯一地表示。

图1 欧拉角示意图Fig.1 Diagram of Euler angles
此模型中没有考虑其他性质力对箔条运动的影响,而只考虑流场对箔条的曳力和箔条所受的重力,相关计算公式为
ua=u0+(I·ω)×ra
(1)
式中:ua为箔条离散分段a的速度;u0为箔条的质心速度;I为体坐标系到定坐标系的转换矩阵;ω为箔条在体坐标系中的角速度;ra为定坐标系中箔条离散分段相对于基准点的位置矢量。
箔条受到的流体曳力计算公式[14]为
(2)
式中:FD为箔条所受的流体曳力;FD,a为箔条离散分段所受的流体曳力;n为箔条离散段数;CD为流体曳力系数;ρc为流场密度;Ap为曳力作用的有效截面积;uc为流场速度;ua为离散分段的速度。
Ap=πdlasinβ
(3)
式中:d为箔条直径,la为箔条离散分段的长度,β为箔条轴向与矢量uc-ua的夹角。
曳力系数CD的计算公式[15]为
CD=0.71+0.07RN
(4)
(5)
式中:Re为箔条的雷诺数;l为箔条的特征长度,对于圆柱形箔条而言为箔条的直径;μ为空气的动力黏度。对于单根箔条,平动方程为
(6)
式中:m为细长箔条的质量;g为重力加速度;s为箔条质心的位移。转动方程为[16]:
(7)
(8)

在运动学计算过程中引入欧拉参数。欧拉参数实际上是一组四元素,由λ0,λ1,λ2和λ34个元素组成。并且这4个元素满足以下关系[17-19]:
(9)
欧拉参数与欧拉角关系[20]为
(10)
欧拉参数表示的定点转动的运动方程为
(11)
再根据欧拉角和欧拉参数之间的关系求出一个时间步之后的欧拉角。
(12)
式中:ψ′,θ′,φ′为一个计算时间步后的进动角、章动角和自转角。
1.2 箔条间碰撞模型
为考虑箔条间碰撞,对计算空间进行网格划分,箔条间的碰撞在这些网格内进行。为了找到不同箔条发生碰撞的位置,本文在箔条离散分段的基础上,将这些离散分段转化为具有等效直径的小球,运用修正后的Nanbu模型,得箔条分段a和同一网格内其他所有箔条分段(除与分段a处在同一根箔条上的其他分段外)的碰撞概率[21]为
(13)
式中:n和N分别为箔条分段的真实数目和取样数目;Dp为箔条分段的等效直径;Gab为箔条分段a和b的相对速度;go为径向分布函数;Δt为时间步长。
go=1/[1-εs/εmax]1/3
(14)
式中:εmax为填充状态时的箔条分段密度,εs为不同时刻各网格内的箔条分段密度。
在箔条分段a总碰撞概率Pa<1时,利用随机数R(0
假设箔条分段a、b分别在箔条i、j上,通过上述方法就找到了箔条i、j发生碰撞的位置,根据动量守恒定律可以获得箔条i和j发生碰撞后的速度和角速度。具体的碰撞模型[22]为
(15)
(16)
(17)
(18)
(19)
(20)
(21)
(22)
式中:下标P代表平行,V代表垂直;ui,uj为箔条碰撞前碰点速度;vi0,vj0为箔条碰撞前质心速度;Ii,Ij为坐标转换余弦矩阵;ωi0,ωj0为碰撞前箔条在体坐标系中的角速度;ri,rj为碰点到箔条质心的位置矢量;v为碰点最大压缩形变时速度;ri0,rj0分别为ri,rj的单位矢量;Pi,Pj为ri0,rj0的并矢张量;viV,vjV为在ri0,rj0垂直方向的速度变化;qi,qj为冲量;e为恢复系数;vi,vj为碰撞后箔条质心的速度;ωi,ωj为碰撞后箔条在体坐标系中角速度;Π为定坐标系中的单位张量;J′i,J″j为箔条在体坐标系中的转动惯量;Ji,Jj为箔条在定坐标系中的转动惯量;e为碰撞过程中的恢复系数,当弹性碰撞时e=1,当完全非弹性碰撞时e=0。
1.3 计算过程
由式(1)~式(22)即可得涉及相互间碰撞的箔条动力学及运动学特征,其中微分方程组由四阶龙格-库塔法求解。具体过程由C++实现。运动参数计算流程图如图2所示。
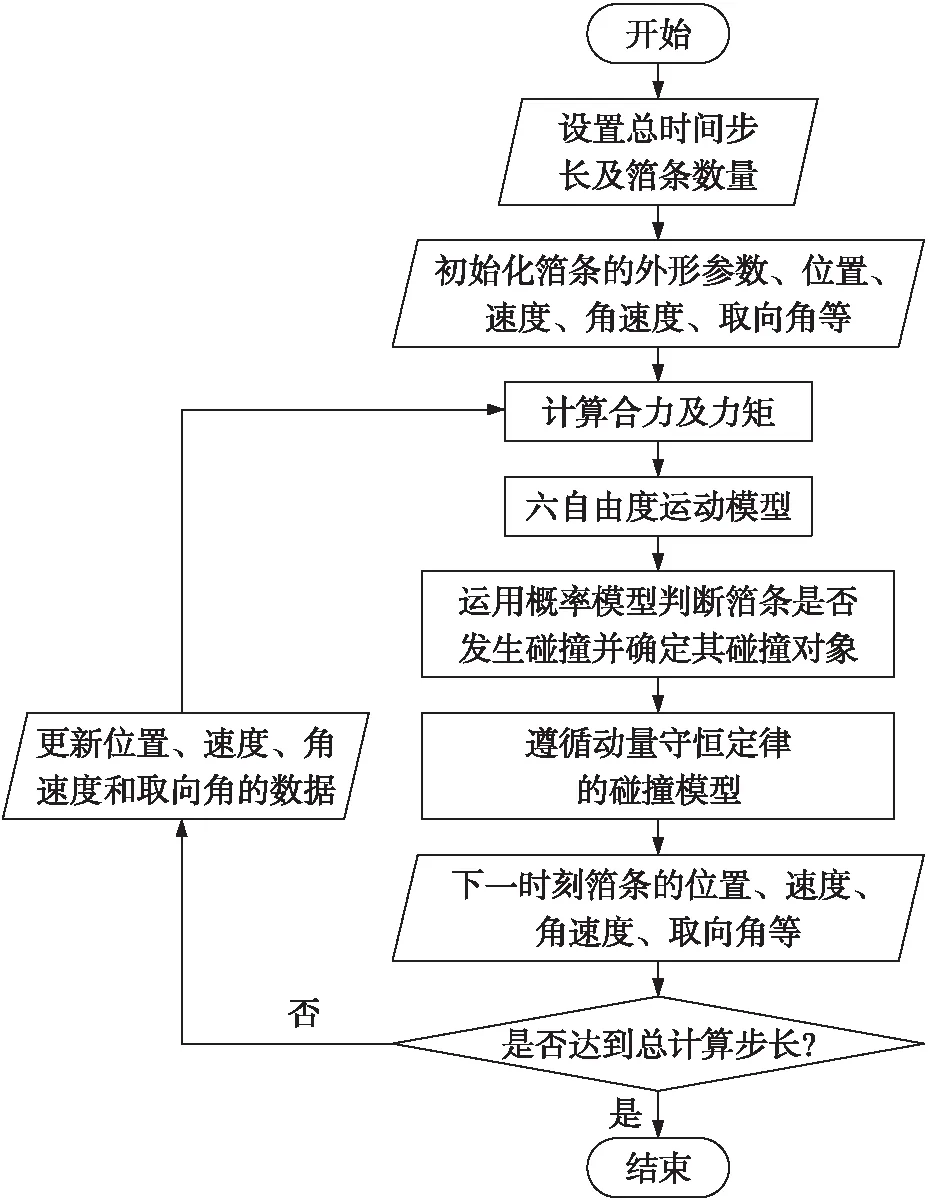
图2 运动参数计算流程图Fig.2 Flow chart of motion parameter calculation
2 数值计算和试验结果对比
设定载体火箭的飞行方向为y轴正向,飞行马赫数为0.8;箔条集束以35 m/s的速度垂直于载体火箭向上出舱,开舱点的坐标为(2,1,1),设定开舱时刻为零时刻,开舱后箔条由集束表面分离。假设不同时刻由箔条集束表面上分离的箔条的进动角ψ、章动角θ、自转角φ分别在0~2π,0~π,0~2π上呈随机分布,角速度ω在体坐标系3个轴上的投影ωξξ,ωηη,ωζζ在0~2 rad/s上随机分布。仿真计算中箔条总数为2 000 根,时间步长为1 ms,计算总时长为1.5 s。
为了验证模型的合理性,进行了近地箔条抛撒试验。针对本文试验背景需求,设计了固体火箭发动机携带干扰弹高速抛撒的箭载试验系统。点火后火箭加速至干扰弹发射所需的模拟速度时,采用延时点火炬点燃干扰弹发射药,箔条集束被抛出。试验时高速摄像机布置在弹道侧方,用于记录箔条集束分离、云团扩散的全过程。试验中通过六通道同步触发器控制火箭与高速摄像机的同步点火与触发。图3为箔条抛撒后不同时刻yz截面云团分布的试验结果和仿真结果。图4为箔条抛撒后xz截面云团仿真结果。

图3 yz截面云团分布图Fig.3 Chaff cloud distribution in the yz section

图4 xz截面云团分布图Fig.4 Chaff cloud distribution in the xz section
由图3和图4中不同时刻云团散布对比可知,当所有箔条抛撒完毕,即t=50 ms时,箔条云团呈较为整齐的锥形分布,y方向分布在4~13 m,z方向分布在1.5~3 m。t=100 ms时,箔条云已基本成型,x方向上分布在1~3 m,yz方向上的最大散布面积已达10 m2以上。可见,箔条多体分离用时很短,能够在100 ms内迅速散开成型。300 ms后云团分布基本稳定,进入沉降阶段,箔条云团整体以一定速度下沉。
表1给出了箔条云团轴向及径向尺寸随时间的变化情况,也反映了箔条云的遮蔽面积与时间的关系,试验结果与仿真结果发展趋势一致。当云团形态达到稳态时,其在轴向上的散布面积可达13 m2,径向上的散布面积可达4 m2。同仿真结果相同的是,试验中云团轴向截面由锥形截面演化为矩形截面。

表1 云团尺寸变化试验与仿真结果对比Table 1 Comparison of cloud size change in experiment and simulation results
3 云团散布特性参数统计分析
3.1 数量分布
数量分布η是箔条散布过程中重要的特征量。图5给出了箔条数量分别沿x,y,z方向的分布情况,从而可以得出箔条云团随时间变化的散布规律。
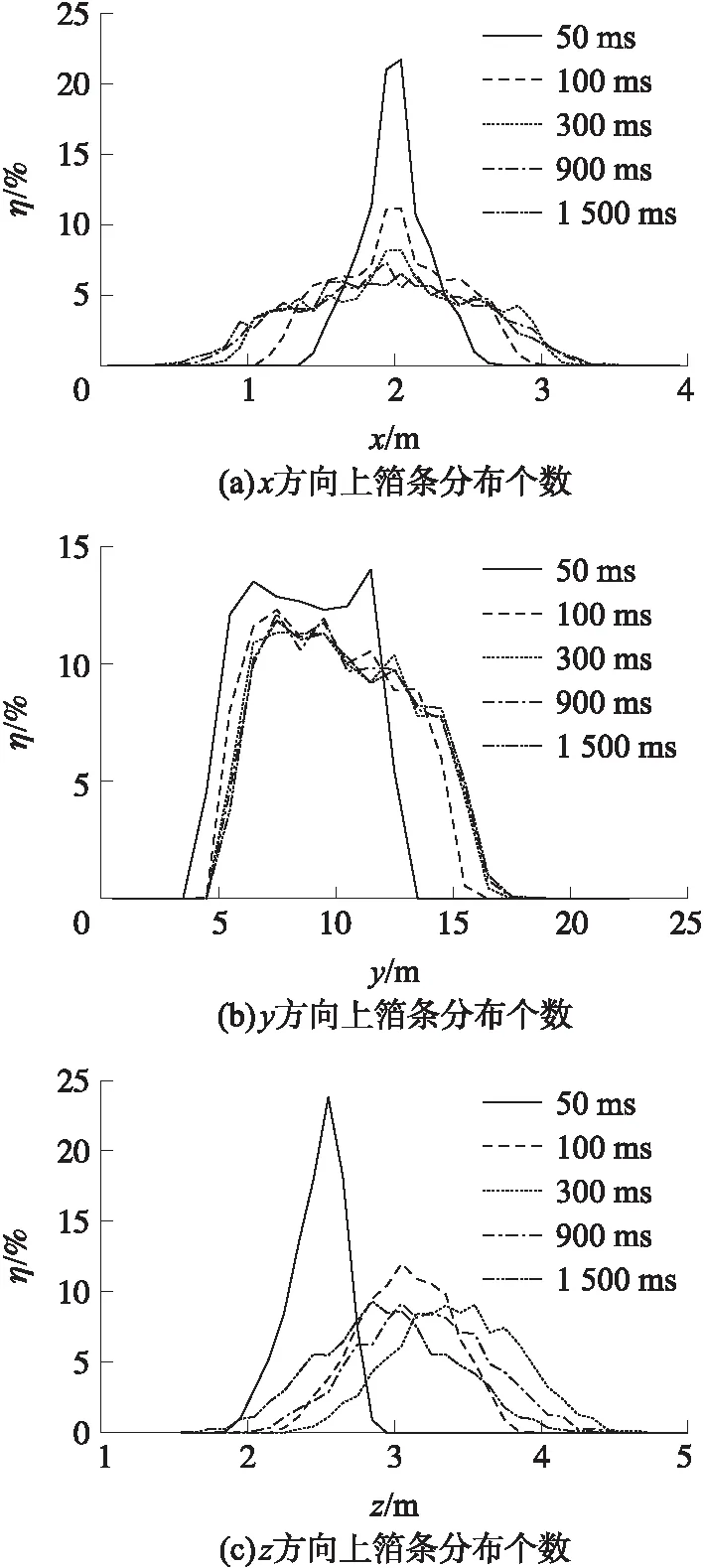
图5 不同方向箔条分布个数Fig.5 Number of chaff in different directions
由图5可知,50 ms时在x方向上箔条集中在1.5~2.5 m之间,随着云团向四周的扩散,箔条散布面积变大,分布逐渐均匀;在y方向上箔条的数量分布在100 ms后基本不再变化,轴向散布的结构已经形成,各时刻数量分布曲线的整体趋势大致相同。z轴上的分布与x轴类似,但由于重力作用,云团进入沉降阶段后以一定速度沿重力方向运动,表现为数量分布曲线整体以相对固定的趋势随时间沿z轴负向移动。
3.2 扩散分布的数字特征
通过讨论扩散过程中箔条位置坐标D的均值、轴向平面与径向平面内箔条云团边界值和方差3个数字特征量,对云团的空间分布进行了分析。
3.2.1 箔条群坐标均值
箔条集群坐标的统计平均值反映了箔条云整体在不同时刻的所在位置,其计算方法为
(23)
式中:D为箔条质心的位置坐标,N为箔条个数。通过计算可得几个特征时刻箔条群空间坐标统计平均值,如表2所示。

表2 箔条位置坐标均值Table 2 Mean value of chaff position
以各方向上箔条位置坐标的平均值作为箔条云质心的位置坐标,即可得出云团整体速度随时间的变化曲线,如图6所示。300 ms后,箔条质心速度在各方向上的分量基本不再发生改变,说明云团整体运动进入沉降阶段。
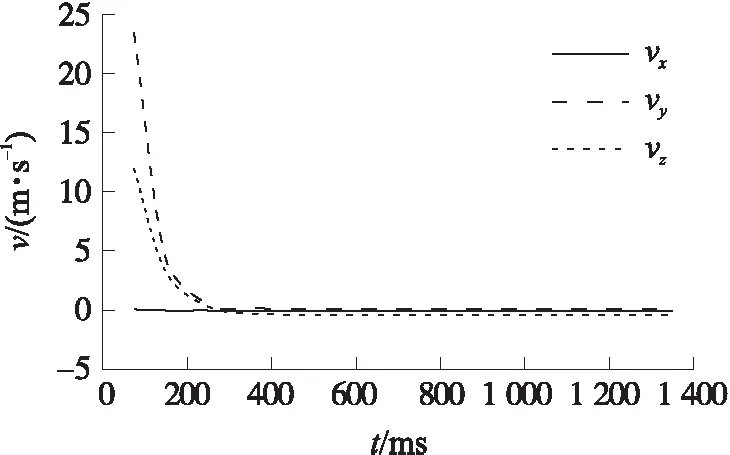
图6 箔条云整体速度变化图Fig.6 Change of overall velocity of chaff cloud
3.2.2 云团边界处箔条坐标值
云团边界值是指某一时刻坐标的最小值和最大值,可以对云团外轮廓进行描述。由图7可以看出,y方向上的边界值曲线在50~300 ms间斜率大幅度降低,这是由于抛撒完成后箔条速度很快衰减进而以低速运动;x方向上300 ms之前的云团尺寸增长速率大于300 ms之后的;300 ms后,所有箔条保持匀速运动,使得整个云团也以一定速度沉降,z方向上云团上下边界值同步减小。

图7 不同方向上云团边界值变化图Fig.7 Cloud boundary changes in different directions
3.2.3 箔条位置坐标偏离均值的方差
将不同时刻各箔条位置和由式(23)计算得出的E代入式(24)中,得到箔条偏离平均值的方差。
(24)
图8为不同时刻箔条云团在各方向上的方差变化曲线。y方向上的方差明显大于x,z方向,这是由于箔条云在y方向上散布区域远大于其他2个方向。300 ms前,方差在y方向上的增长速度较快,这是因为此时位于云团头部和尾部箔条的速度相差很大,云团内部箔条位置分布变化较大。300 ms后,方差在x,y,z方向上都基本不再变化,箔条分布结构已基本形成。
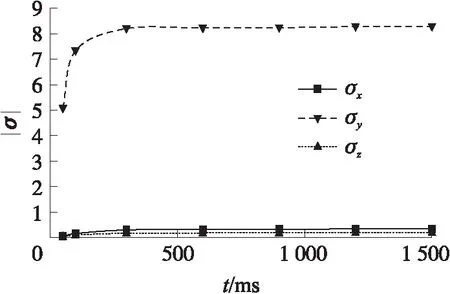
图8 3个方向方差变化图Fig.8 Change in variance in x,y and z directions
4 结束语
本文在刚体动力学及碰撞概率模型的基础上,对箔条在牵连速度为270 m/s下的抛撒散布过程进行了数值模拟,分析了云团散布轨迹,并开展试验,验证了模型的准确性,进而对箔条云团的整体性能及云团内部箔条的分布规律进行了分析。可以得到以下结论:
①牵连速度是影响箔条云团成型和散布的关键因素。箔条云团在0.1 s内基本成型,0.3 s后云团内箔条的数量分布情况基本不再随时间变化。箔条集束能够在0.3 s内形成稳态云团,云团成熟后在轴向上的散布面积可达13 m2,径向上的散布面积可达4 m2,云团边界值的发展趋势在0.3 s时发生明显变化。
②进入沉降过程后,云团整体运动速度稳定,其中在y方向上的速度为0.12 m/s左右,z方向上的速度为-0.4 m/s左右。由于y方向上不同位置的箔条速度相差较大,因而在该方向上箔条分布更具不均匀性。
③在牵连速度为270 m/s的情况下抛撒箔条,仿真结果与实验结果都表明箔条云团轴向截面经历了由锥形向长方形变化的过程。说明该模型能很好地描述高牵连速度下抛撒的云团散布过程,为后续开展不同牵连速度的箔条抛撒散布研究提供理论依据。

