含流体相应力杂交单元等效弹性模量的分析

邱莹宇，郭 然

(昆明理工大学 建筑工程学院，昆明 650504)

页岩是沉积岩中的一种，具有十分明显的层理构造[1]。页岩气是指以吸附或游离且有时还带有流体相的形态赋存于泥页岩中的非常规天然气[2]。页岩气在中国资源储量丰富，地域分布广泛。页岩气开采能缓解我国常规油气产量不足、煤化石燃料引起环境污染等问题，已成为中国绿色能源开发的重要领域[3]。中国页岩气埋藏深，赋存条件差，自然丰度低[2]，高效开发理论与产能评价处于起步阶段，因此，高效开采面临更多的困难和挑战[4]。而无论是在用水力压裂手段[1]开采页岩气时，还是处理页岩中含有流体的大量微小孔洞时，不可避免地会出现流固耦合的数值模拟问题。因此，带有流体的固体单元的研究具有重要意义。

卞学鐄[5]在1964年创建了假设应力有限元方法，即应力杂交元。最初的应力杂交元是通过修正余能泛函建立的，假定单元中存在满足平衡方程的应力场，单元边界满足力的平衡条件，并且通过对界面节点位移进行插值获得边界位移。1988年下半年，Accorsi根据最小势能原理推导了一个新单元[6-7]。2016年，黄永霞等[8]进行了颗粒增强复合材料有效模量的Voronoi单元有限元法分析。2017年，Zhang等[9]使用Voronoi单元法提出了含孔洞单元的修正余能泛函形式，在少量单元的情况下，获得了在内部压力作用下的应力分布。2019年，韩宁等[10]模拟了颗粒夹杂复合材料的力学性能,分析了网格划分对复合材料力学分析精度的影响。同年，Han等[11]提出了一种新的单元，其裂纹从内孔的边缘开始，并且在单元内和单元间扩展。他们采用的Voronoi单元网格划分方法在处理形状简单和尺寸较小的微结构方面具有优势，但当孔体积分数相对较大或彼此之间的距离非常接近时(如图1所示)，将很难进行网格化。

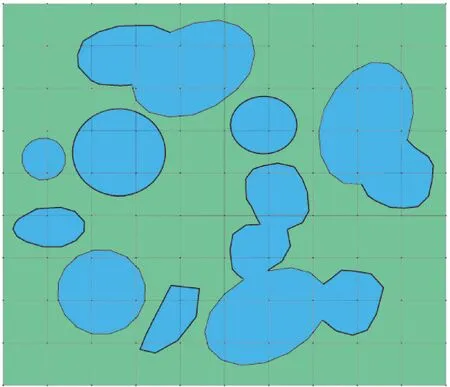
图1 页岩中流体微结构的分布情况(蓝色代表流体，绿色代表页岩)Fig. 1 Distribution of fluid microstructure in shale (blue represents fluid, and green represents shale)

针对大量含流体孔洞的页岩问题，笔者提出了一种采用均匀网格并满足流固界面压力平衡的新的流固耦合单元fluid-structure coupling stress hybrid element(FCSHE)。该单元可以进一步推广，解决一般性的流固耦合问题。

通过对简单四单元模型FCSHE与MARC模型的应力分布情况以及等效弹性模量的对比验证，证明单元的有效性后，建立多个模型，分别通过改变形状、体分比、空间分布位置和半径，研究了等效弹性模量变化的影响因素[12-16]。

1 含流体相的应力杂交单元(FCSHE)

杂交元是基于最小余能原理的有限元模型，其中应力函数为场变量，余能泛函如式(1)所示[5]。

(1)

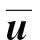
为了满足表面力的边界条件

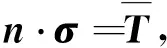
(2)

(3)

式中：n+和n-分别是相邻单元边的法向向量，使用拉格朗日乘子法引入2个约束，以获得修正余能泛函[2]

(4)

式中：∂Ve是所有单元的边界，∂Ωte是给定面力的边界，u是单元边上的位移。

如图2所示，在流体和固体的界面处，满足表面力的平衡条件

nfs·(σs-σf)=0，

(5)

式中：σs是固体侧应力，σf是流体侧应力，nfs是流体侧指向固体侧的交界处的法向矢量。

图2 流固交界处的典型单元Fig. 2 Typical element at fluid-solid junction

引入该约束条件得到修正余能泛函

(6)

式中：nes是元素的外部固体边界上的外部法线向量；nef是流体边界上的是从流体侧指向固体侧的界面处的法线向量；σ是在单元域中满足平衡的应力场；ues是在单元固体边界上的位移；uef是在流体边界上的位移。

在固体部分Ωes中，将自平衡应力场引入单元中[5]：

σs=Psβs。

(7)

式中：Ps为固体部分的插值矩阵，βs为固体部分的待求系数列阵。

在流体部分Ωef中，考虑液体压强为一个常数，此时，σx=σy，τxy=0，所以

(8)

(9)

式中：x和y是构造出的应力函数的自变量；若为二阶函数，

(10)

注意，在静态分析中，页岩孔中流体的压力场通常是恒定的，因此以下所有模型均采用方程式(8)。

引入位移插值功能后，边界位移可以用节点位移表示：

单元固体侧的外部边界∂Ωes

ues=Lqes，

(11)

单元流体侧的外部边界∂Ωef

uef=Lqef，

(12)

流固交界面∂Ωi

ui=Lqi。

(13)

式中：qes是固体界面的节点位移；qef是流体界面的节点位移；qi是流体和固体交界面的节点位移；L是插值函数。

将方程(7)(8)和(11)～(13)代入方程(6)，得到离散系统修正余能泛函的弱形式。根据修正余能泛函的平衡条件：

(14)

(15)

可以得到运动关系的弱表达形式

(16)

其中，

(17)

(18)

(19)

(20)

(21)

(22)

式中：Ωs是固体区域，Ωf是流体区域，Ωis是流固交界面上固体部分的边界，Ωif是流固交界面上流体部分的边界，nis是流固交界面上固体部分的法向向量，nif是流固交界面上流体部分的法向向量，Lis是流固交界面上固体部分的插值函数，Lif是流固交界面上流体部分的插值函数。

从上面可以看出，应力参数在单元中的位移表达式为

β=H-1GQ，

(23)

其中，

(24)

(25)

(26)

(27)

节点位移qes、qef和qi关于系统Πsf的总能量的一阶偏导可以表示为

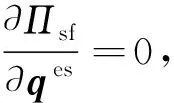
(28)

(29)

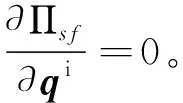
(30)

随即可以得到每个单元中的运动关系弱表达形式

(31)

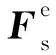
(32)

其中，

(33)

将方程式(23)和(32)组合在一起，得到表达式(34)来求解广义位移：

(34)

得到求解广义位移的方程组

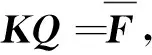
(35)

其中，

(36)

方程(35)的刚度矩阵为

(37)

式中：Ke表示单元的刚度，e表示所在单元。

2 算 例

2.1 验证模型

在此算例中，建立了一个带孔的正方形板模型，分析了其在平面应力状态下的线弹性静力学行为。正方形板边长为0.40 mm，在其中心有一个半径为0.05 mm的孔，并充满了水(不考虑流动)。由于MARC软件中没有液体单元，因此通过在孔中施加压力(从FCSHE获取)来表示含水孔。FCSHE模型由4个单元组成，MARC模型由11 482个单元组成。边界条件如图3(a)所示，水平位移为0.15 μm。在模型仿真分析中使用的材料属性如下：

固体：弹性模量Es=72.0 GPa，泊松比νs= 0.33。

流体：弹性模量Ef=2.18 GPa，泊松比νf= 0.50。

由于没有流固耦合材料的解析解，所以采用与MARC结果作对比的形式来验证有效性。图3中的3幅图分别是工况图(a)、由FCSHE和MARC得到的模型(b)和(c)，图4～6为FCSHE和MARC分别得到的σx、σy和τxy应力云图。一条线上的路径和结果显示在图7中。比较结果发现，尽管存在一些细微的差异，应力的总体分布、应力集中的位置以及应力场值的趋势都非常相似，而且应力集中出现在流固交界面的上下两侧，不同于固体材料的左右两侧。

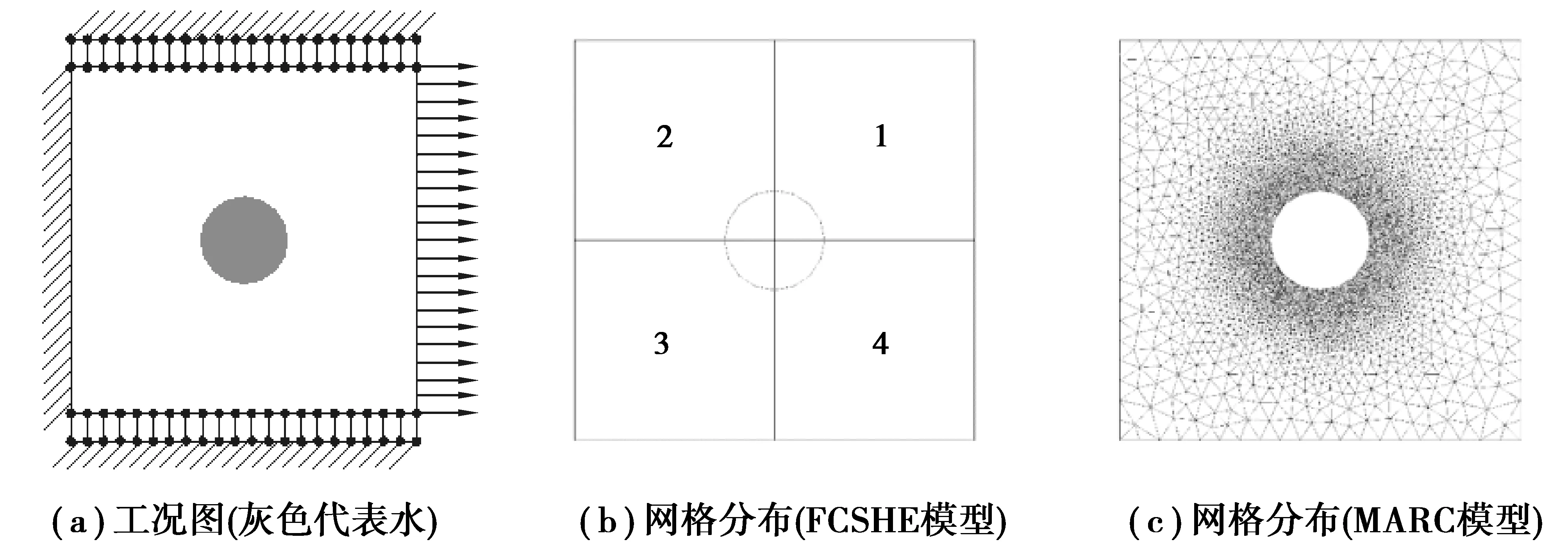
图3 工况及网格划分图Fig. 3 Boundary conditions and mesh diagram

图4 FCSHE(a)和MARC(b)的应力在x方向上的应力分量云图Fig. 4 Contour plots of stress x of FCSHE (a) and MARC (b)

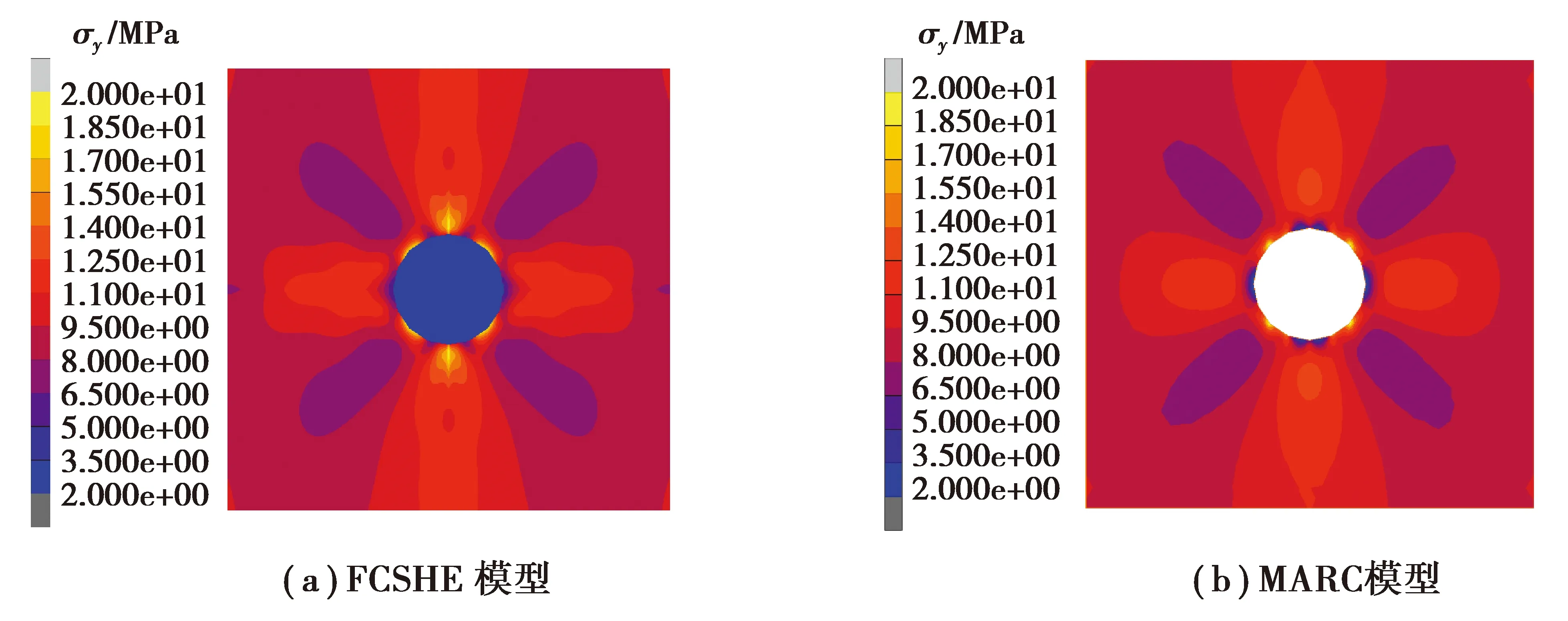
图5 FCSHE(a)和MARC(b)的应力在y方向上的应力分量云图Fig. 5 Contour plots of stress y of FCSHE (a) and MARC (b)

图6 FCSHE(a)和MARC(b)的切应力的应力云图Fig. 6 Contour plots of shear stress xy of FCSHE (a) and MARC (b)

图7 应力路径图Fig. 7 Diagram of stress on the path

在FCSHE方法中，流体与固体之间的界面上节点很少，并且每2个节点之间的位移采用线性插值法，因此界面上的位移场相对简单。在MARC中，界面处节点很多，因此应力场会更加丰富。这是两个模型的计算结果不同的主要原因。

经计算可知，FCSHE法得出的等效弹性模量为62.84 GPa，MARC中算出的等效弹性模量为62.60 GPa，两者相对误差为0.385%，证明了FCSHE法的有效性。

2.2 等效弹性模量的影响因素

2.2.1 体分比对等效弹性模量的影响

在8 mm×12 mm的长方形上建立模型，其上分布有10个含水孔。边界条件为：上下两侧约束y方向位移，左侧约束x方向位移，右侧给定一个0. 3 μm的方向向右的位移。模型一共100个单元，外边界含121个节点，流固交界面的边界包含4个节点。含水孔体分比w分别为4%、8%、12%。在模拟分析中所用材料的弹性模量和泊松比与模型验证中所用材料相同。

图8为不同体分比的单元模型示意图，图9为等效弹性模量随体分比的变化情况。很容易看出，材料的等效弹性模量随孔的体分比增大而减小，且基本呈线性变化。通过对体分比的研究得知，可以通过减小含流体孔洞材料的体分比提高材料的等效弹性模量。

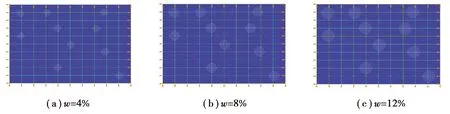
图8 不同体分比单元模型Fig. 8 Element model with different volume fractions

图9 等效弹性模量随体分比变化Fig. 9 The variation of equivalent elastic modulus with volume fraction

2.2.2 半径对等效弹性模量的影响

8 mm×12 mm的长方形上分布有若干圆形含水孔。边界条件为：上下两侧约束y方向位移，左侧约束x方向位移，右侧给定一个0.3 μm的方向向右的位移。单元模型一共64个单元，外边界含81个节点，流固交界面上有4个节点。单元最大边数为6，最大内边数为7。保持孔体分比都为7%，孔的半径r为0.4,0.5,0.6 mm(单元模型如图10所示)。

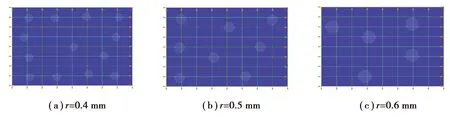
图10 不同半径单元模型Fig. 10 Element model with a different radius

在孔的体分比不变的情况下，半径与孔的数量成反比。图11显示的是等效弹性模量随半径的变化情况，由图可知，半径增大时，等效弹性模量也逐渐增大，不呈线性。

图11 等效弹性模量随半径变化Fig. 11 The variation of equivalent elastic modulus with radius

2.2.3 形状对等效弹性模量的影响

8 mm×12 mm的长方形上分布有10个含水孔。边界条件为：上下两侧约束y方向位移，左侧约束x方向位移，右侧给定一个0. 3 μm的方向向右的位移。单元模型一共64个单元，外边界含81个节点，流固交界面上有4个节点。单元最大边数为6，最大内边数为6。形状改变方差控制了孔的长短轴，长短轴的取值符合正态分布式(38)。当Svar为0时，孔的长短轴相等，孔呈圆形。当Svar值增大时，保持其他控制参数不变，形状改变方差Svar分别为0.00、0.10、0.15和0.20。形状改变方差越大，孔越扁平，当它为0时，孔为圆形。

(38)

式中：μ为平均数；σ为标准差，即Svar的算术平方根；a、f(a)为孔的长短轴。

图12为不同方差单元模型图，图13为方差在0.00～0.20区间时等效弹性模量的变化情况。由图13可知，在0.00～0.10区间时，等效弹性模量随方差增大而增大。在0.10～0.20区间时，等效弹性模量随方差增大而减小，且减小的幅度较大。如要得到符合正态分布的规律曲线，需要大量的样本。

图12 不同方差单元模型Fig. 12 Element model with different variances

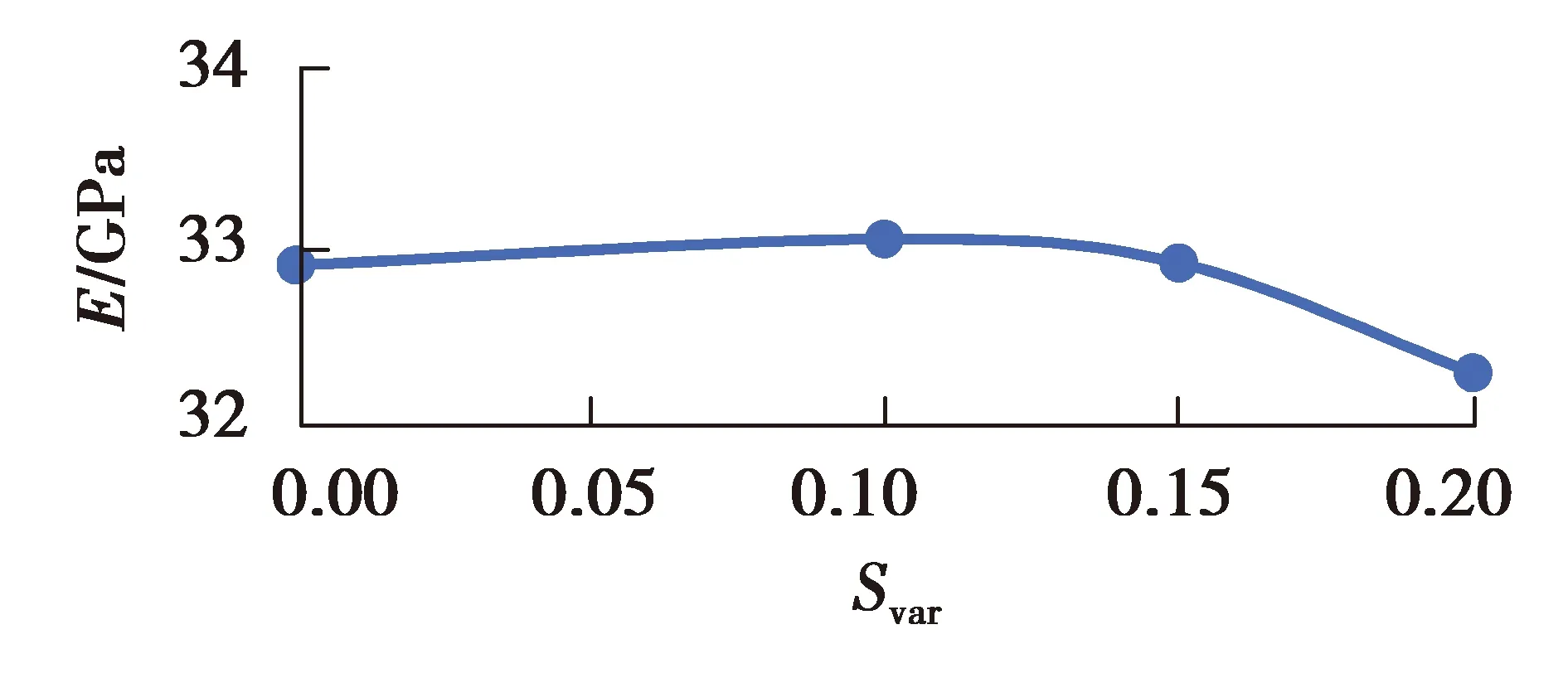
图13 等效弹性模量随方差变化Fig. 13 The variation of equivalent elastic modulus with variance

2.2.4 空间分布对等效弹性模量的影响

在8 mm×12 mm的长方形上分布有3个圆形含水孔，孔半径为0.5 mm。边界条件为：上下两侧约束y方向位移，左侧约束x方向位移，右侧给定一个0.3 μm的方向向右的位移。单元模型一36个单元，外边界含49个节点，流固交界面上有4个节点。单元最大边数为6，最大内边数为3。保持其他控制参数不变，改变孔的空间分布位置，以3个孔的中心点连线与水平线的夹角为角度Sa，研究Sa分别为0°、30°、45°、60°时(如图14所示)等效弹性模量的变化情况。由图15可知，在0°到60°区间内，等效弹性模量随角度Sa增大而减小，并且几乎呈线性变化。

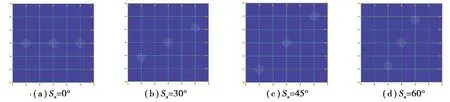
图14 不同角度单元模型Fig. 14 Element model with different angles

图15 等效弹性模量随角度变化Fig. 15 The variation of equivalent elastic modulus with angle

3 结 论

基于普通应力杂交元原理，推导了一种带有新的流体相的固体单元(FCSHE)，在处理页岩中大量孔的问题时，该单元可以大大减少计算量。它既包含流体又包含固体，适合作为流固耦合界面上的单元，可以很好地解决流固网格的过渡问题。建立了典型的四单元模型与普通商业有限元计算软件MARC作对比，两者之间应力分布基本一致，等效弹性模量相对误差在0.4%以内，证明了其有效性。进一步分別研究了形状、体分比、空间分布位置和半径变化时模型等效弹性模量的变化。结果显示，不同形状对等效弹性模量影响不大；同体分比时，随含流体孔半径增大，等效弹性模量随之非线性增大；体分比增大时，等效弹性模量呈线性下降；当角度逐渐增大时，等效弹性模量逐渐减小，并且下降幅度逐渐减小。