质点与刚体相对运动的几何直解法
李志强,李 龙,耿 亮,饶邦政
(1. 广西易城蓝图科技有限公司,530002,南宁;2. 中国建筑股份有限公司,100044,北京;3. 中建工程产业技术研究院有限公司,101300,北京)
0 引言
土木建筑、车辆机械等工程领域的许多技术问题,在一定条件下可以用运动学的原理和方法加以解决[1-2]。以往,运动学的求解方法(不妨称之为“原方法”)多为“先拆解,后合成”,即无论对于质点还是刚体,先将其运动拆解为多种分运动,逐个分析清楚各项分运动的模式和规律后,再进行合成求解;常用的方法或技巧有速度与加速度的合成定理、基点法、速度瞬心、速度投影定理等;原方法相对熟悉和习惯,但有时存在一定的不方便或不足之处,譬如较为抽象、不够直观、适用面窄等。
调研发现[3-8],有学者做过有别于原方法的相关研究,此类方法结合工程中的曲柄摇杆机构、凸轮、连杆机构等机械要素,其解法和结果可运用于相关工程领域;然而,此类方法在标量方程组物理量方向的表达,以及几何图形分解的规律等基本方面仍没有涉及到。
本文在前人研究的基础上,提出一种以标量计算为主的简化求解思路,不妨称之为“直解法”,即首先直观地表达运动学问题中的几何图形,列出几何关系方程后,按要求令等式两侧对时间求一阶或二阶导数,最终代入已知的初始或边界条件后求解方程组。
1 关于直解法
1.1 方法介绍
直解法的思路是直接处理模型的几何关系。位移、速度、角速度、加速度、角加速度等都是矢量,但在此法中仅求解其大小,它们的方向还需要根据求解结果的正负和具体问题条件进行判断。首先将问题背景剥离,抽象成简单的几何图形,列出图中几何关系表达式,这是对问题所给图形的最直观表达,是零阶等式。式中所含的长度、角度都是关于时间的函数。令零阶等式等号两侧同时对时间求导数,得到一阶等式。式中长度关于时间的导数就是速度,角度关于时间的导数就是角速度;速度与角速度也是关于时间的函数。令一阶等式等号两侧同时对时间求导数,得到二阶等式。式中速度关于时间的导数就是加速度,角速度关于时间的导数就是角加速度。联立诸式,代入已知的初始条件,以及简单易察的隐含条件(如某条边是固定不动的,则其速度为0,某点匀速运动则其加速度为0,等等)求解未知变量。需要指出的是,此处介绍的直解法是不考虑物理量方向在内的,其方向需要在求出标量解后,根据解的正负并结合具体情境单独判断;高阶矢量方程组的求解本文不作介绍。
以图 1为例对所述的方程组做简单说明。
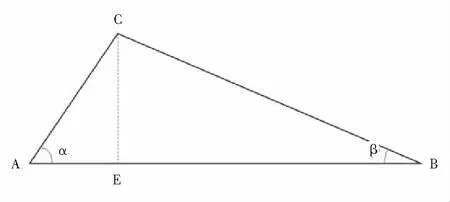
图1 直解法例图
列出图形中的几何关系等式,从C点向AB边引垂线,用AC边和BC边的三角函数表达AB边长度:
AB=ACcosα+BCcosβ
(1)
令此式等号两侧对时间求导。需要注意的是此处均为隐函数求导:

(2)
再令此式等号两侧对时间求导,同样是隐函数求导:

(3)
再对另一个方向列式,用2个自然边的三角函数表达垂线:
ACsinα=BCsinβ
(4)
令此式等号两侧对时间隐函数求导:
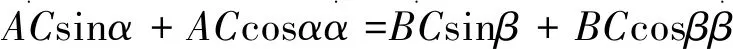
(5)
再令此式等号两侧对时间隐函数求导:
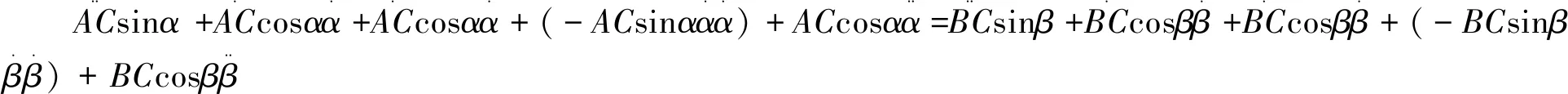
(6)
联立诸式得到方程组,该方程组就是直解法的基础,结合具体问题代入提示的所有条件,可得其中的任意变量的值,再根据值的正负判断矢量方向。需要指出的是,一个几何图形可以有很多组表达式,如何列式应紧扣问题背景和已知条件,达到最便捷解答的目的。列式时,应尽量多地将几何图形中不变化的边列入,比如杆件、滚轮半径等不随时间变化的恒定值,如此,令其对时间求导数后得0可以消去,大大简化运算。通常,零阶方程组中一个等式表达的是几何图形中真实存在的一边,它与它的一阶、二阶导数往往与某待求速度或加速度相关;另一个等式表达的是过某一顶点垂直于该边的辅助边(类似于三角形的“高”),它与它的一阶、二阶导数往往与某待求角速度或角加速度相关。
此后若问题中还有更复杂、更高阶的要求,如急动度(也称“加加速度”或“力变率”)或角急动度等,则在二阶等式的基础上再对时间求导数得到三阶等式即可。
1.2 直解法与原方法的对比
直解法与原方法各有优缺。原方法的优势在于求解过程中可以使用一些有用的规律和技巧,以便有效提升求解效率,而其缺点同样在于求解依赖于这些规律和技巧,一旦不具备使用条件或条件隐含很深不易察觉,则求解难度大幅提升;此外,运动学的拆解与合成充满抽象感,当问题要素较多、背景较为复杂时,对研究对象运动模式和规律的理解和把控就变得困难。总之,原方法的适用面较为狭窄。直解法的优势在于非常直观,因而称之为“直解法”;此外,此法适用面较宽广,而且可解更高阶问题,缺点在于计算复杂,要求求解者对于微分学和三角函数相关知识的掌握高度熟练。
2种方法都是对运动学本质的表达,并行不悖、相辅相成,区别在于观察角度和描述方法不同。求解时对于2种方法的选取需要充分观察问题所给条件。譬如,求速度和角速度时采用原方法或直解法均可,求加速度和角加速度时宜采用原方法,求更高阶问题推荐采用直解法。
2 算例
以下对2个算例进行计算分析,同时采用2种方法,并将它们的计算过程和结论进行对比。
2.1 算例1
椭圆规尺AB以等速u沿水平导槽向右运动,尺AB长l。试求B端沿铅直导槽运动的速度和尺AB的角速度(见图 2)。

图2 算例1示意图
2.1.1 解法1(原方法:基点法) AB做平面运动,其上A点速度大小、方向已知,可取为基点;故B点速度vB可由下式确定:
vB=vA+vBA=u+uBA
(7)
需要注意的是,式(7)是矢量式。式中只有vB和vBA2个未知量,可作出速度平行四边形如图 2所示,可得B点速度大小:
vB=ucotφ
(8)
方向向下。
AB的角速度:
(9)
方向逆时针。
2.1.2 解法2(原方法:瞬心法) 在此瞬时A点和B点的运动方向已知,即A点水平向右,B点垂直向下。按照速度瞬心的规律,AB作为平面转动中的刚体,一定存在某一点瞬时速度为零而AB上各点都绕这个点转动。作垂直于u的垂线、垂直于vB的垂线交于C点,C点就是刚体AB此刻的瞬心,如图3所示。

图3 算例1解法2示意图
因为角速度相同,而v=ωr,绕C各点速度大小与点到瞬心距离r成正比,因而有:
(10)
vB=ucotφ
(11)
方向向下。
2.1.3 解法3(原方法:速度投影定理法) 在此瞬时A点和B点的运动方向已知,即A点水平向右,B点垂直向下。按照速度投影定理,平面图形上任意两点的速度在该两点连线上的投影相等,那么令A点速度和B点速度都投影到AB上,有:
ucosφ=vBsinφ
(12)
vB=ucotφ
(13)
方向向下。
2.1.4 解法4(直解法) 在此瞬时A点和B点的运动路径已知,即A点水平,B点垂直。如图 2所示,A点速度反映在AO的变化上,B点速度反映在BO变化上:
AB=l=OAcosφ+OBsinφ
(14)
令等号两侧对时间求导数,得到:

(15)
其中,OB·cosφ=OA·sinφ,故此消去,求解得到:

(16)
因此从大小上来说vB=u·cotφ,趋势上是使OB变小,故方向垂直向下。此外,还可以列出一个方程,用2条边来表达垂线OE,即:
OAsinφ=OBcosφ
(17)
令等号两侧对时间求导数:

(18)
整理得到:

(19)
显然OA·cosφ+OB·sinφ就是AB边,长度为l。联立(16)和(19)得:
(20)
因此从大小上来说ω=u/(l·sinφ),趋势上是使φ变小,故方向为逆时针。
2.1.5 评价 在算例1中,就一道非常基础的问题,从不同的侧面去观察图形都可以找到突破口,原方法可以用3种技巧给出答案,其中的瞬心法比较有助于理解刚体的转动;而直解法则是顾名思义直接列出几何关系求解,一气呵成,对于刚体运动全过程中的任意时刻都有相当的解释力,并且计算工作量也不大。
2.2 算例2

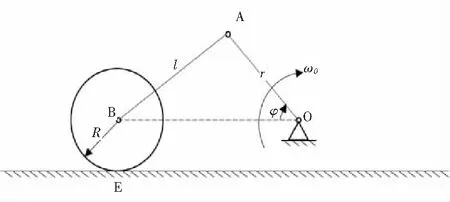
图4 算例2示意图
2.2.1 解法1(原方法) 机构具有一个自由度,杆AB及轮B均做平面运动,关键在于分析B点的速度与加速度。
1)速度求解。杆AB做平面运动,vA=rω0,方向垂直于OA,vB沿水平方向,如图5所示。

图5 算例2解法1示意图(a)
应用速度投影定理,得:
vBcos30°=vAcos15°
(21)
vB=1.115rω0
(22)
轮B做无滑动的滚动,接触点处vE=0,E为轮B的瞬心,于是有:
(23)
(24)
ωB方向为逆时针,vD方向垂直于ED连线。
对于杆AB,将vA,vB向与AB垂直的方向投影,有:
vBsin30°=vBA-vAsin15°
(25)
vBA=vBsin30°+vAsin15°=0.816rω0
(26)
由此可得杆AB的角速度ωAB为:
(27)
方向为顺时针。
2)加速度求解。首先,采用基点法分析B点的加速度,如图 6、图7所示。

图6 算例2解法1示意图(b)

图7 算例2解法1示意图(c)
对于杆AB,已知aA=rω02,以A为基点,B为动点,则有:
(28)
需要注意的是,此等式为矢量式。式中:
(29)
aBAτ大小未知,方向与AB垂直。将式(28)向AB投影,则有:
(30)
(31)
对于轮B,因为做纯滚动,其角加速度可由定义αB=dωB/dt求得,即:
(32)
方向为顺时针。轮上B点的加速度已知,以B点为基点,得:
(33)
(34)
2.2.2 解法2(直解法) 过A做AP垂直于OB交于P点,如图8所示。
根据图8中的几何关系列零阶方程组如下:
OB=OAcosφ+ABcosα=rcosφ+lcosα
(35)
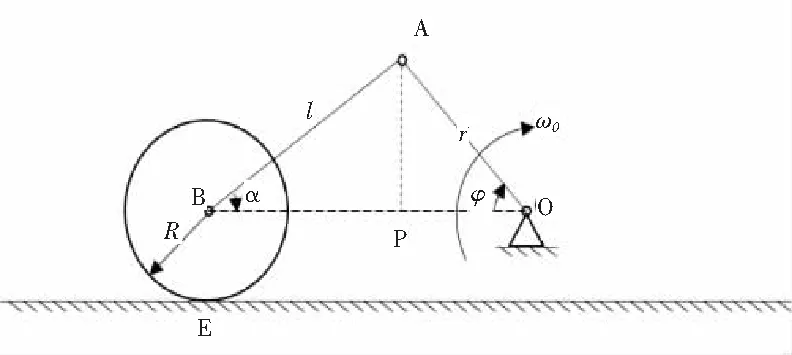
图8 算例2解法2示意图
OAsinφ=ABsinα,即
rsinφ=lsinα
(36)
令零阶方程组等号两侧同时对时间求导可得一阶方程组:
(37)

(38)
因机构两臂均为刚体,因此它们的长度任何时候都不会变化,因此一阶方程组可简化为:
(39)
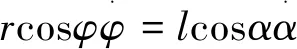
(40)
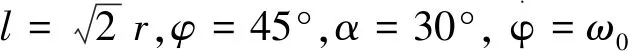
(41)
这是AB的转动角速度,其大小为0.577ω0,趋势是使∠ABO增大,因而方向是逆时针。再将结果代入式(39)可得:
(42)
这是B点的速度,其大小为1.115rω0,趋势是使OB变短,因此方向向右。轮B做无滑动的滚动,接触点处vE=0,E为轮B的瞬心;代入R=0.5r,得到ωB并合成vD如下:
(43)
(44)
由纯滚动性质和已求得的B点速度方向可知,ωB方向顺时针,vD斜向右上45°。令一阶方程组等号两侧同时再对时间求导得到二阶方程组:
(45)
(46)
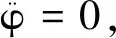
(47)
(48)

(49)
方向为顺时针。纯滚动不考虑科里奥利加速度,加速度为切向加速度与法向加速度的矢量叠加。
(50)
(51)
因解答过程较为复杂,不是本文的重点,此处不赘述。
最后检查结算过程及其所有结果,通过量纲进行简单的核算:速度的量纲都为LT-1,加速度的量纲都为LT-2,角速度的量纲都为T-1,角加速度的量纲都为T-2,核算通过。
2.2.3 评价 在算例2中,使用原方法对机构的速度和加速度的分析变得复杂了许多,对于高阶物理参量的方向确定也有所不便,还有赖于对图形进一步观察,在具体求解过程中还需要用到多种技巧才行;而直解法,则显示出相当程度的优势。当然,需要指出的是,直解法的二阶方程组的运算量显著提升,但这恰是计算机的长处,相信不难克服。
3 结论
1)本文针对质点与刚体的相对运动提出了一种新的解法,即直解法,论证了该法是成立且合理的,并具有直观性强、适用面广、能够处理高阶运动学问题、便于计算机程序大规模高速度辅助运算等优点。
2)本文对比2种方法后认为原方法计算量小但是抽象,直解法计算量大但是直接;通过2个算例对2种解法进行了较为详细的说明,并通过解答过程分析了2种解法的适用场合:一阶的运动学问题可用2种方法,二阶问题宜用原方法,三阶及以上的问题宜用直解法。需要说明的是判断二阶及以上运动学问题中的物理量的方向,需要结合运动学知识和具体情境进行判断,不能简单依靠任意一种方法所给出的解答直接给出。
3)理论上运动学问题中的几何关系越复杂越突显直解法的优势;为使用直解法解题,尤其是考虑矢量在内的计算量庞大的问题,可以运用计算机编程辅助计算。直解法的发展将有利于提升运动学分析的效率和准确度,在土木工程、机械工程等领域均可广泛应用。

