信号增降采样与滤波实验教学研究
魏少明,林应斌,王 俊
(北京航空航天大学 电子信息工程学院,北京 100191)
数字信号处理是20 世纪中叶发展起来的一门以微积分、差分方程等数学知识为基础的工程科学技术。智能制造、人工智能和航空航天等新产业、新经济的快速发展对数字信号处理教学培养提出了新的要求[1]。
在数字信号处理的实际应用中,通常会面临改变一个离散时间信号采样率的问题,要么将它增加某个量,要么将它减少某个量。通过升降采样处理,以不同的采样率得到以同一个连续时间信号为基础的新的离散时间序列,该过程称为采样率转换[2-5]。
为实现对干扰信号的滤除,可以采用无限冲激响应(IIR)滤波器和有限冲激响应(FIR)滤波器两种离散时间滤波器[6-8]。
FIR 滤波器有精确的线性相移,在设计上比IIR 有更多的可控之处,适用于各种实际情况[9]。FIR 滤波器的设计采用多项式逼近,具体方法包括窗函数法、频率抽样法和最佳逼近法。窗函数法比较简单,它的频率特性是理想频率响应与窗函数傅里叶变换的周期卷积,因此,频率特性主要取决于窗函数的类型和长度。频率抽样法比较直观,但由于频域采样会造成时域混叠,为提高滤波器性能,可以在过渡带加上0~1 之间的过渡点[10]。本实验主要采用窗函数设计法[11]。FIR 滤波器的实现,可以采用两种方式实现:时域卷积和差分方程[12]。
一、实验原理
采样是将一个信号(即时间或空间上的连续函数)转换成一个数值序列(即时间或空间上的离散函数)。采样定理指出,如果信号是带限的,并且采样频率大于信号频率的两倍,即fs≥2fm,那么,原来的连续信号可以从采样样本x[n]中通过重构公式完全恢复出来其中,采样周期为T=1/fs[13]。在MATLAB 中提供了理想内插器函数interp(x,I),调用方法是[y,h]=interp(x,I),该函数用于将数组x 中的信号以I 倍原采样率重新采样,所得重采样数组y 是原数组的I倍长。其中,输入参数:x 为有限长离散信号序列,可以是实数也可以是复数;I 为增采样倍数,要求为整数。输出参数:y 为重采样数组,是原数组x 的I 倍长;h 为用于插值的滤波器系数。
滤波器是一种能够让某些频率分量通过而拒绝其他频率成分或对某些频率成分进行修正的系统。窗函数法设计FIR 滤波器时,在MATLAB 中提供的滤波设计函数有fir1(),此函数可以设计低通、高通、带通和带阻滤波器[14]。设计低通或带通滤波器时,调用方法是b=fir1(N,Wn),其中,N 是滤波器的阶数;Wn 是归一化截止频率,对于低通滤波器,它是0 和1 之间的一个数,对于带通滤波器,它是包含通带边界的向量[Wn1,Wn2],其中0<Wn1<Wn2<1;向量b 是滤波器的脉冲响应序列。设计高通滤波器时,调用方法是b=fir1(N,Wn,’high’),其中N 为偶数。设计带阻滤波器时,调用方法是b=fir1(N,Wn,’stop’),其中Wn 是一个双元素向量。对于窗函数类型的选择,调用方法是b=fir1(N,Wn,taper),其中taper 是长度为N+1 的窗函数序列,可以采用不同的MATLAB 函数来产生对应的窗函数序列taper=blackman(N),taper=hamming(N),taper=hanning(N),taper=chebwin(N),taper=kaiser(N,beta)。
MATLAB 中同时提供了另一种FIR 滤波器设计函数fir2,可以设计任意形状幅度响应的FIR 滤波器。调用方法是b=fir2(N,fpts,mval),其中,fpts 是频率点向量,在0 到1 范围内以递增顺序排列,其中采样频率被假定为2 Hz;mval 是对应频率点的幅度值向量,和fpts的长度一样;b 是长度为N+1 的脉冲响应序列。为使用不同的窗函数序列,调用方法是b=fir2(N,fpts,mval,taper),其中taper 为窗函数序列。
FIR 滤波器的实现,可以采用两种方式实现:时域卷积和差分方程。FIR 滤波器是一个线性时不变系统,其时域输入和输出关系可用卷积的方法描述,y[n]=x[n]×h[n]。对于FIR 滤波器,滤波器的脉冲响应h[n]为有限项,范围从0 到M,信号x[n]通过滤波器的输出为y[n]=x[n]×h[n]。通过卷积运算,可实现对输入信号的滤波处理[15-16]。MATLAB 提供了计算线性卷积的函数conv,调用方法是w=conv(u,v),其中u 和v 是有限长度序列,w 是卷积结果序列。如果u 和v 的长度分别为N 和M,则w 的长度为N+M-1。FIR 滤波器的差分方程实现,MATLAB 提供了滤波函数filter,调用方法是y=filter(b,a,x)。其中b为FIR 滤波器的脉冲响应序列,a 设置为1,x 为滤波器输入信号,y 为滤波输出信号。
信号的频谱分析,通过快速傅里叶变换实现。MATLAB 提供了快速傅里叶变换函数fft(x,N),调用方法是X=fft(x,N),该函数用于实现离散信号序列x 的N点FFT 计算。输入参数:x 为有限长离散信号序列,可以是实数也可以是复数;N 是FFT 变换的长度。当缺N时,就以x 序列的长度作为FFT 变换的长度。设置N后,当x 序列的长度大于N 时,取x 序列N 长作FFT 变换(即对x 序列进行截断);当x 序列的长度小于N 时,在x 后补零至N 长再作FFT 变换。输出参数:X 为x 的N 点FFT 结果。MATLAB 同时提供了频谱居中搬移函数fftshift(x),调用方法是y=fftshift(x),该函数用于将fft 函数结果的零频率点移至频谱中心。输入参数:x 为fft 函数计算结果。输出参数:y 为频谱居中后的FFT 结果。
二、实验要求
实验要求学生能够掌握实验所涉及的增降采样和滤波器设计与实现的原理,并能够实际应用。学生需要编写实验程序,对不同的正弦信号进行增降采样、滤波和频谱分析。其中,信号的重采样、滤波器设计、滤波器实现部分,有不同的MATLAB 实现方法,学生需要对不同的方法进行尝试和分析,从而寻找综合性能和效率最优的方法。
结合实验的数据运用MATLAB 绘制出实验程序的曲线,提高学生对MATLAB 的编程能力及知识运用能力。结合曲线分析实验中的问题,得出实验结论,提高学生对采样定理,增降采样方法,滤波器设计与实现,以及傅里叶变换的理解。
三、实验过程
对不同频率的正弦信号进行增降采样、滤波和频谱分析,绘制信号的时域波形和频谱图。
1.对模拟频率为f0=3.5 kHz 的单频正弦信号x(t)=cos(2πf0t)进行采样,采样率为fs=8 125 Hz,得到原始采样信号x[n]=x(t)|nT,n=0,1,…,7 999。对采样信号隔点抽取,形成2 倍降采样信号y[n]=x[2n]。以采样率2fs对x(t)进行采样,得到2 倍采样信号x0[n]=x(t)|nT0,n=0,1,…,通过重构公式将原始连续信号重构出来,以采样率2fs对xr(t)进行采样,获得2 倍内插信号z[n],n=0,1,…,15 999;通过理想内插器函数interp 对x[n]进行2 倍重采样,获得2 倍内插信号z1[n],n=0,1,…,15 999。
分析z[n]和z1[n]之间的差异,从中选择最优的2 倍内插信号,并分析选择的原因。绘制2 倍采样信号与2倍内插信号的时域波形以及波形差;绘制原始采样信号、2 倍降采样信号、2 倍采样信号和2 倍内插信号的频谱图。
2.对模拟频率为f0=3.5 kHz 和f1=0.5 kHz 的双频正弦信号x(t)=cos(2πf0t)+cos(2πf1t)进行采样,采样率为fs=8 000 Hz,得到原始采样信号x[n]=x(t)|nT,n=0,1,…,7 999。对采样信号隔点抽取,形成2 倍降采样信号y[n]=x[2n]。通过重构连续信号,,以采样率fs对y(rt)进行采样,获得内插信号z[n],n=0,1,…,7 999。通过理想内插器函数interp 对y[n]进行2 倍重采样,获得内插信号z1[n],n=0,1,…,7 999。
分析z[n]和z1[n]之间的差异,从中选择最优的内插信号,并分析选择的原因。绘制原始采样信号与内插信号的时域波形以及波形差;绘制原始采样信号、2 倍降采样信号和内插信号的频谱图。
3.模拟频率为f0=3.5 kHz 的正弦原始信号,以及模拟频率为f1=3.8 kHz 的正弦干扰信号,两个信号在时域的混合信号为x(t)=cos(2πf0t)+cos(2πf1t),以采样率fs=8 125 Hz 分别对正弦原始信号和混合信号进行采样,得到原始采样信号x0[n]=cos(2πf0t)|nT,混合采样信号x[n]=x(t)|nT,n=0,1,…,7 999。设计一个FIR 滤波器,让f0=3.5 kHz 的正弦信号通过,对f1=3.8 kHz 的正弦信号具有不低于50 dB 的抑制,混合采样信号通过滤波器的输出为y[n]。
采用fir1 和fir2 进行滤波器设计,采用时域卷积和差分方程进行滤波器实现。从中选择最优的滤波器设计和实现方法,并分析选择的原因。绘制原始采样信号与滤波信号的时域波形及波形差;绘制原始采样信号、混合采样信号和滤波信号的频谱图,分析在滤波信号中,对干扰信号的抑制是否不低于50 dB;分别调整两个正弦信号的频率,重复上述过程,并分析滤波器长度的变化规律。
四、实验结果
根据实验流程进行MATLAB 仿真,对三种情况下的信号进行时域增降采样、滤波和频谱分析。
单频正弦信号的时域增采样和频谱分析,结果如图1 所示。
从图1 可以看出,2 倍采样信号与2 倍内插信号在时域和频域上基本一致,表明在满足采样定理的条件下,信号的增采样可以得到比较理想的结果。
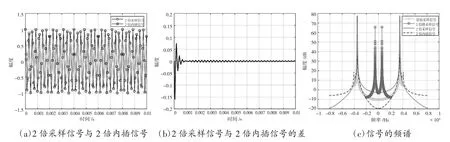
图1 单频正弦信号的时域增采样和频谱分析结果
双频正弦信号的时域降采样、增采样和频谱分析,结果如图2 所示。
从图2 可以看出,原始采样信号与内插信号在时域和频域上差异很大,其中对满足采样定理的信号分量,信号的增采样效果比较理想,但是对不满足采样定理的信号分量,无法进行有效的信号增采样。

图2 双频正弦信号的时域降采样、增采样和频谱分析结果
混合信号的时域滤波和频谱分析,结果如图3 所示。
从图3 可以看出,通过对比混合采样信号和滤波信号的频谱,可以看出滤波器对正弦干扰信号的抑制可以达到50 dB,满足滤波器的实验设计要求。不过由于滤波器的群延迟,导致滤波信号与原始采样信号在时域上无法完全一致。通过该实验可以让学生加深对滤波器设计和滤波效果的理解。
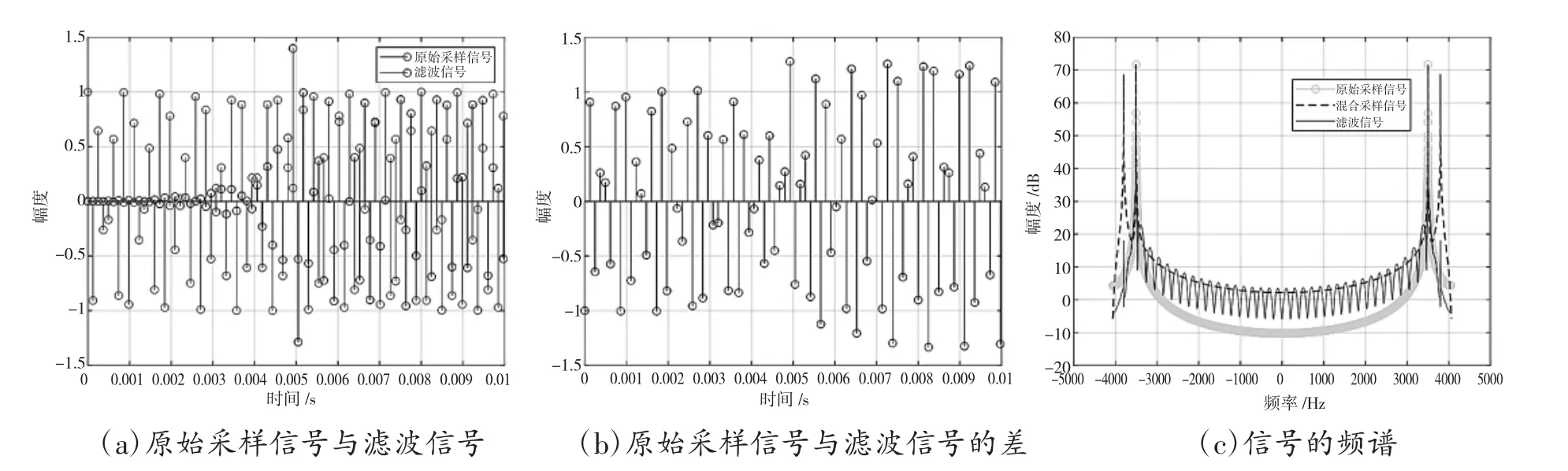
图3 混合信号的时域滤波和频谱分析结果
五、实验考核
本实验的过程是一个比较完整的仿真设计实验,需要经历学习研究、方案论证、实验调试和设计总结等过程。鼓励学生针对实验需要解决的问题,尝试不同的解决思路,结合实验所得曲线、图表分析不同思路的理论原理和优缺点,并能结合思考题举一反三、深入理解和透彻掌握实验所涉及数字信号处理的知识点,实现知识的内化。实验考核部分分为以下几个部分。
(1)实验结果检查:检查学生的实验操作规范,实验结果准确合理。检查过程中,让学生现场修改实验参数,然后运行信号采样和滤波程序,考察学生是否能够进行合理的实验结果展示,是否能够准确阐述实验结果产生的原因。
(2)现场提问:对照学生的实验结果,对实验现象、实验原理等环节进行提问,学生须现场验证或回答,要求能从实验原理出发论证实验现象,或能从实验现象出发探寻其中的实验原理。尤其是信号的重采样、滤波器设计及滤波器实现部分,学生需要展示不同MATLAB实现方法的差异,从中选择性能最佳的方法,并阐释不同方法的内在机理和选择性能最佳方法的原因。
(3)实验数据:检查学生在实验过程中整理的数据是否完整、全面,绘制的实验图表是否清晰、直观。
(4)实验报告:检查学生的实验报告是否具有规范、完整性,对实验原理的理解是否透彻,是否能根据实验现象独立思考做出总结,是否能正确回答实验思考题。
六、结束语
为了让学生深入掌握数字信号处理的信号采样、滤波和频谱分析的相关知识点,文章设计了信号增降采样和滤波实验。本实验为MATLAB 仿真实验。通过对三个不同正弦信号的采样和滤波,实现采样率的转换和信号滤波。让学生既能够真正理解数字信号处理在实际工程中的应用,又能够巩固对增采样、降采样、滤波器设计、滤波器实现和快速傅里叶变换的理解。本实验将理论与实际问题的解决相结合,将抽象的理论形象化、具体化,促进学生对抽象理论的理解;通过不同解决方法的实验、分析与比较,进一步激发学生的探索与学习热情。通过整个实验过程,培养了学生的自主学习、独立思考与综合分析能力。

