城镇化进程中水电站建设对河流连通性的影响研究与实践
王申芳,杨晓灵,梁雯珊
(珠江水资源保护科学研究所,广东 广州 510611)
河流连通性的概念最早是由Amoros和Roux在1988年提出的,Amoros和Roux认为河流连通性是河流水系的一项重要特征,可以用来描述河流水系的景观特征[1]。至20世纪末,这一观点已普遍为人们所接受。夏继红等[2]在2017年也提出河流连通性常用于描述不同河流景观在空间结构和功能特性上的关联程度。河流连通性具有纵向、横向、垂向和时间4个维度特征[3],其中纵向维度(即纵向连通性)是指物质、能量等在河流纵向(源头至河口)上的运输迁移顺畅度[4],在城镇化进程中受人类活动干扰最多、影响也最为普遍[3]。
国内外学者广泛开展了河流连通性的相关研究,先后提出了综合指标法[5-6]、空间图论法[7]、图论-水文法[8-10]、图论-生态法[11-12]、水文-水力学法[13]、景观法[14]、基于GIS的计算与评价方法[15-16]等多种河流连通性计算方法。夏继红等[2]在对图论法、水文水力学法、景观法、生物法、综合指标法等多种河流连通性研究方法适用性和优缺点对比分析成果的基础上,提出综合指标法通过建立多指标综合评估体系可对河流水系连通性进行科学、合理的评价,可为流域水资源宏观管理提供科学决策依据。徐薇等[17]基于长江上游地区水电开发资料和鱼类生境数据的收集,以河流纵向连通性指标为核心,初步构建了长江上游主要河流水系水生态敏感性评价指标体系。侯佳明等[18]在传统阻隔系数法的基础上,引入位置修正系数,提出了改进阻隔系数法。
河流连通性决定着流域(区域)的水资源配置、水生态环境、水景观格局以及经济社会发展等众多方面。与此同时,伴随着社会经济的不断发展,人类活动也在不同程度地改变着河流水系的连通性,尤其是城镇化进程中大量的水电站建设对河流纵向连通性造成了很大影响,部分河流甚至出现了减脱水河段,给河流水生态环境造成了不可逆影响。2010年,水利部陈雷部长指出要积极推进河湖水系的连通性恢复工程,以恢复河湖水系的连通为途径,加快构建国家、区域、流域等各个层面的水资源优化配置格局[19]。自此之后,国内众多学者更加着力于河流水系连通性的机理研究与实践,譬如:贺达等[20]在调查长江流域干流和主要支流过鱼设施建设现状的基础上,对河流纵向连通性进行了初步评估,为提升长江流域水系连通性和水生态环境质量提供了参考;侯佳明等[18]成功运用改进阻隔系数法对黄河流域1960—2018年主要河流纵向连通性及其年际变化趋势进行了评价;朱晨春等[21]采用纵向连通性指标和分段线性回归方程等分析了西北江三角洲河道纵向连通性的变化特征,为西北江三角洲网河区河道水资源管理提供了参考。
纵观河流水系纵向连通性研究与实践,目前国内学者普遍对长江、黄河、珠江等大型流域河流连通性研究较多,对中小型流域的重视程度相对较低,开展研究的相关课题也相对较少。本文以广东省云浮市南山河流域为研究区域,采用河流纵向连通性指标法(Vertical Connectivity Index,VCI)、阻隔系数法、改进阻隔系数法定量评估水电站建设对中小型流域河流纵向连通性的影响,同时结合树状水系连通性指数(Dendritic Connectivity Index,DCI)[22]研究结果,提出河流连通性恢复建议,以期为中国水利水电开发建设,尤其是中小型河流水系管理提供可参照的模式。
1 研究区域概况
南山河流域所处位置特殊,在云浮文史方面有着特殊的背景,是云浮文化三大起源地之一。南山河又称淡水河,发源于广东省云浮市云安区石城镇禾枪顶东麓,海拔696 m,从西南向东北流经云浮市区中心,进入云安区都杨镇降水后注入西江。中段有绛坑水、高峰水、云楼水汇入,流域面积255 km2,主河长46 km,主河道平均坡降3.03‰,多年平均流量5.74 m3/s,年径流量1.81亿m3,是唯一贯穿云浮市的河流。
研究区域共有16座中小型水电站,其中5座为闸坝式水电站,其余均为引水式水电站,16座水电站均建设了拦河闸坝,坝高在1.5~50.0 m,且均未建设过鱼设施(表1、图1)。据调查,八和水电站已于2019年4月报废拆除,鸿景、金水伦、扶卓二级等3座水电站目前处于暂停运状态,其余12座水电站均正常运行。

表1 研究区域内拦河建筑物建设情况

备注:序号16八和水电站已于2019年4月报废拆除。
2 研究方法
本文基于夏继红等[2]、徐薇等[17]、侯佳明等[18]的研究成果,采用VCI法、阻隔系数法、改进阻隔系数法等指标法定量评估水电站建设对南山河流域河流纵向连通性的影响;同时,运用王强等[3]、Cote等[22]提出的DCI法,针对研究区域提出进一步提高流域水系纵向连通性的具体方案。
2.1 VCI法[17]
河流纵向连通性指标(VCI)常用于表征单位长度河流上已建和在建拦河建筑物的数量,其数值越大,表明该河流受拦河建筑物的影响越大,生态恢复力越差,生态敏感性越高。该指标分级标准见表2[23],其数学表达式可表述为:
VCI=DN/RL×100
(1)
式中 DN——某一河流上已建和在建的拦河建筑物数量,座;RL——该河流的长度, km。

表2 河流纵向连通性指标分级标准
2.2 阻隔系数法[24-25]
阻隔系数法通过计算单位长度河流上的纵向连通性指数(Cj)来表征河流的连通程度,其阻隔系数越大,表明该河流纵向连通性受阻隔影响越大。其数学表达式可表述为:
(2)
式中Cj——第j段河流的纵向连通性指数;n——不同类型拦河建筑物的种类数,种;Ni——第i种拦河建筑物的数量,座;ai——第i种的拦河建筑物相应的阻隔系数;Lj——第j河段的河流长度, km。
2.3 改进阻隔系数法
在阻隔系数法的基础上,引入位置修正系数(bi),用以定量计算拦河建筑物所处位置对本级河流连通性和本级河流与下级河流之间连通性的阻隔程度。其数学表达式可表述为:
(3)
其中:bi=(bLi+bQi)/2
式中Cj——第j段河流的纵向连通性指数;ai——第i种的拦河建筑物相应的阻隔系数;bi——第i种的拦河建筑物的位置修正系数;Lj——第j河段的河流长度, km;bLi——拦河建筑物对本级河流纵向连通性影响的位置修正系数;bQi——拦河建筑物对本级河流与所汇入干流(或河口)之间连通性影响的位置修正系数。
2.3.1阻隔系数ai
在传统阻隔系数的基础上增加橡胶坝、水闸2种拦河建筑物类型,并赋予相应数值(表3)[18]。

表3 改进后的阻隔系数取值
2.3.2本级河流位置修正系数bLi
通常认为拦河建筑物位于河流中间位置对河流的阻隔影响最大,随着拦河建筑物向两岸偏移,其对河流的阻隔影响逐渐减小。bLi计算方法如下:
(4)
式中Lai——第i个拦河建筑物所在位置距离河流源头的距离, km;Lbi——第i个拦河建筑物所在位置距离汇入干流(或河口)的距离, km;Lj——第j段河流的总长度, km;α——标准化系数,通常取值0.78。
2.3.3下级河流位置修正系数bQi
通常认为河流流量越大,河流中可通过的生物量越大[24]。通过计算拦河建筑物所处位置的多年平均天然径流量与河段汇入干流(或河口)处的多年平均天然径流量的比值(bQi),可以反映拦河建筑物对该河流与下级河流之间的阻隔程度。bQi值越小,表示流量差异越大,拦河建筑物对该河流与下级河流间的阻隔影响就越大。bQi计算方法如下:
(5)
式中Qi——拦河建筑物所在位置多年平均天然径流量,m3/s;Qj——该河段汇入干流(或河口)处的多年平均天然径流量,m3/s;β——标准化系数,通常取值0.5。
2.4 树状水系连通性指数(Dendritic Connectivity Index,DCI)[22,26]
DCI指数常用于描述鱼类在河流两个随机点之间的自由游动概率,其主要受河流中拦河建筑物的数量和阻隔渗透性等因素影响。拦河建筑物的阻隔渗透性表征鱼类在顺流和溯流时通过拦河建筑物的能力,其值越大,表明鱼类通过拦河建筑物的能力越大,河流纵向连通性越高。DCI指数计算公式如下:
(6)
(7)
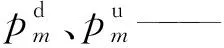
该公式在实际应用中通常假定:①拦河建筑物本身不占用河道长度,不影响河流总长度;②鱼类通过拦河建筑物的能力是完全独立的,不受其上、下游拦河建筑物的影响;③2个拦河建筑物之间的河段是完全联通的,故水系的纵向连通性为整个水系任意2个河段之间连通性的总和。
3 纵向连通性影响评估
本文利用ArcGIS软件对南山河流域水系进行数字化,基于水电站的地理位置,获取每个河段的长度和河网的总长度,分别采用VCI法、阻隔系数法和改进阻隔系数法计算每条河流的纵向联通指数,采用树状水系连通性指数评估法计算整个水系的DCI指数,由此评估水电站建设对河流纵向连通性和流域水系连通性的影响。
鉴于水电站可通过能力的影响因素比较复杂,且不属于本文研究内容,本次研究不考虑1970—2020年间河道长度的变化;同时,研究范围内所有水电站均建有闸坝,且均未建设过鱼设施,假设流域内水电站从上游至下游的可通过能力均为1,从下游至上游的可通过能力均为0[3]。根据水电站建成的时间和地理位置可知,1980、1990、2000、2010、2020年南山河流域水电站数量依次为3、5、15、16、15座(图2)。

a)1980年
3.1 河流纵向连通性评估
采用VCI法、阻隔系数法和改进阻隔系数法计算1970—2020年南山河及主要支流的河流纵向连通性,计算结果见表4、5。经对比分析可知。
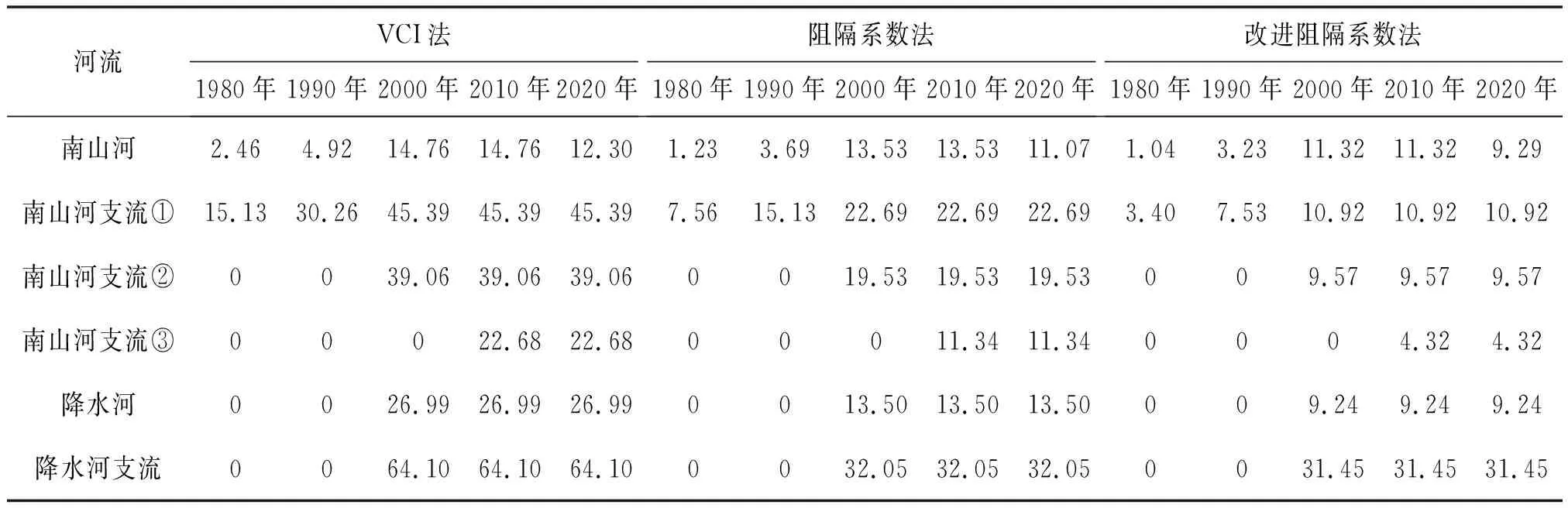
表4 南山河流域河流纵向连通性指数计算结果
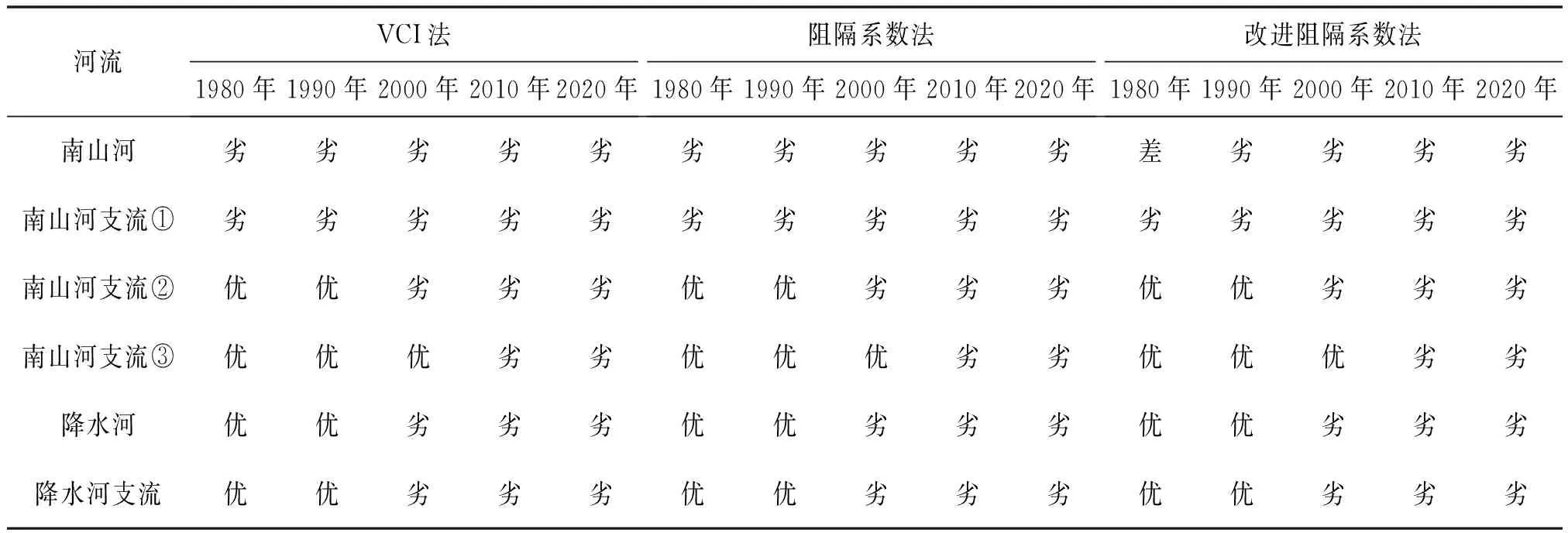
表5 南山河流域河流纵向连通性评估结果
a)改进阻隔系数法通过引入位置修正系数,可充分考虑水电站所在位置对河流带来的阻隔影响,采用该方法进行河流连通性的评估结果更加科学合理。以南山河为例,VCI法和阻隔系数法计算得出1980年的河流纵向连通指数分别为2.46、1.23,河流连通性评价结果均为“劣”;改进阻隔系数法在考虑水电站地理位置后,计算得出的河流纵向连通指数为1.04,河流连通性评价结果从“劣”提升至“差”。
b)相比大型河流,中小型河流的连通性受水电站建设的影响更为显著。以南山河和南山河支流①为例,1980年2条河流的水电站数量均为2座,采用改进阻隔系数法计算河流的纵向连通指数分别为1.04、3.40,河流纵向连通性评估结果分别为“差”、“劣”;同样,以南山河支流③和降水河支流为例,2010年两条河流的水电站数量均为1座,采用改进阻隔系数法计算河流的纵向连通指数分别为4.32、31.45,河流纵向连通性评价结果虽均为“劣”,但降水河支流的连通性受水电站的影响更为显著。
3.2 流域水系纵向连通性评估
采用树状水系连通性指数法计算得出1980、1990、2000、2010、2020年南山河流域水系的DCI指数依次为86.32、82.10、28.11、28.02、28.55。经对比分析可知。
a)在城镇化建设进程中,水电站(尤其是未建设过鱼设施的中小型水电站)建设将大幅降低流域水系的连通性,对水系连通性产生显著的不利影响;1990—2000年间,随着城镇化建设进程的加快,南山河流域水电站数量显著增加,从1990年的4座增加至2000年的15座,流域水系的DCI指数由86.32下降至28.11,降幅为67.4%,流域水系的连通性显著下降。
b)当水电站数量较少、河流水系状况接近天然连通状态时,水电站建设对流域水系连通性的影响更为显著。1980—1990年,新建降水1座水电站,研究范围内水电站总数由3座增加至4座,DCI指数从86.32下降至82.10,降幅为4.9%;2000—2010年,新建蓝坑1座水电站,研究范围内水电站总数由15座增加至16座,DCI指数从28.11下降至28.02,降幅仅为0.3%。
4 河流连通性恢复的建议
基于水电站对南山河流域水系连通性的影响研究成果,采用树状水系连通性指数评估法分别计算拆除每个水电站后整个水系的DCI指数(表6),以此为基础分析每个水电站对流域整个水系连通性的影响,为恢复水系连通提供参考。从表6中可以看出,每个水电站对流域水系连通性的影响均不同:位于南山河干流的鸿景水电站对整个流域水系连通性的影响非常突出,拆除该电站后,流域水系DCI指数可增加12.82;其次是城北、新中、滩冲水电站,各电站拆除后流域水系DCI指数可增加3.26、2.26、1.71;位于南山河支流①的云楼一站、云楼二站、云海水电站对整个流域水系的连通性影响很小,各电站拆除后流域水系DCI指数仅可增加0.03、0.03、0.03;金水伦、扶卓二级水电站对整个流域水系的连通性影响则基本可忽略不计。
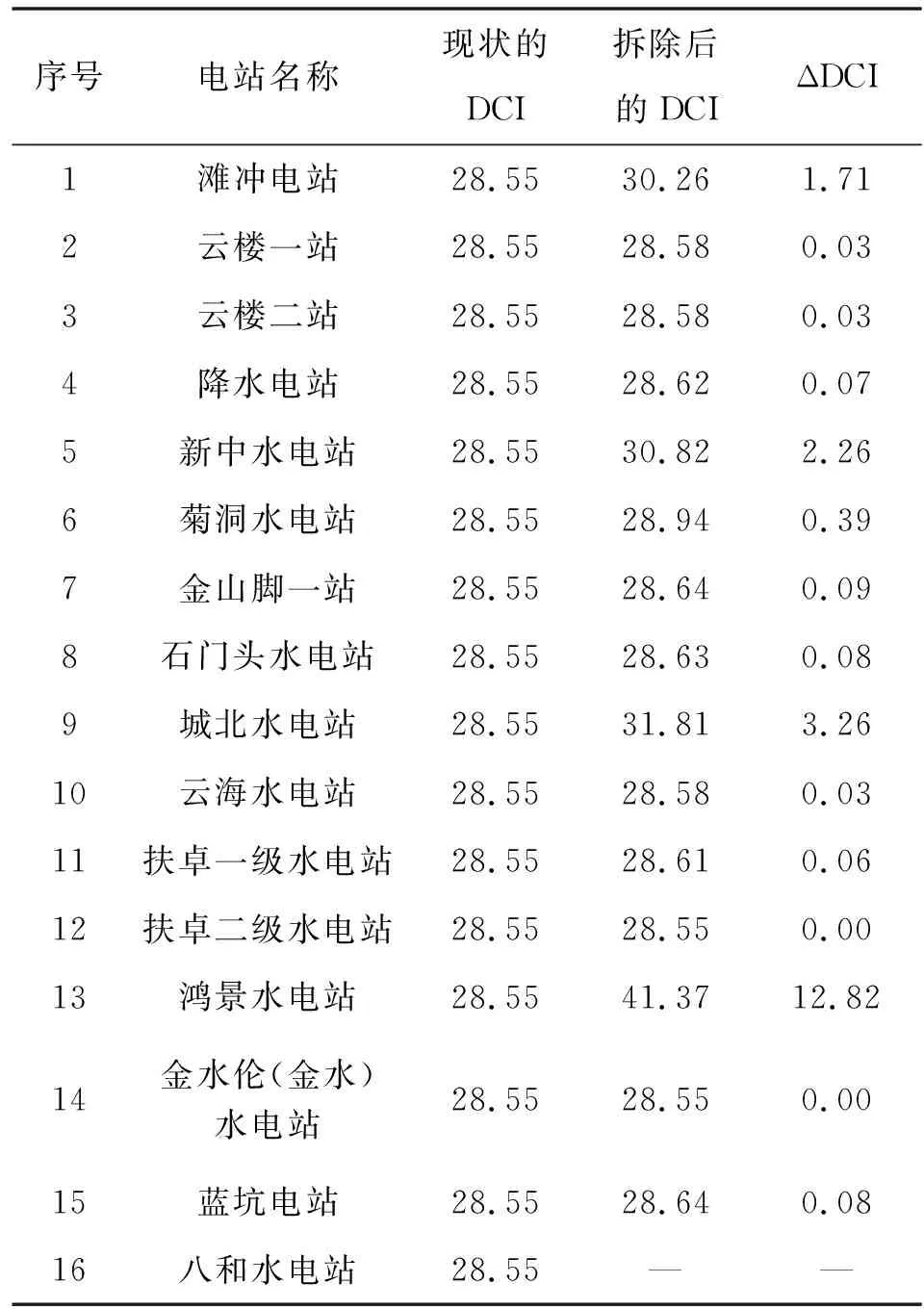
表6 水电站拆除前后流域水系DCI变化情况
另一方面,水电站建设过鱼设施可以恢复鱼类的洄游通道,使鱼类能顺利的上行或下行,在维持河流生态系统的连通性、保护珍稀鱼类、维持河流的生物多样性等方面均具有重要意义。如贺达等[20]在调查长江流域干流和主要支流过鱼设施建设现状的基础上,对河流纵向连通性进行了初步评估,提出大坝有无过鱼设施、鱼类能否自行通过过坝设施、鱼类通过过坝设施的效率如何,可以直接反映大坝阻隔效应的程度。而大坝阻隔效应的程度是影响河流连通性的一项重要指标,可见,对现有水电站增设过鱼设施亦会大幅提高河流的纵向连通性。
综上所述,在恢复流域水系连通性时,可依据ΔDCI的值确定水电站拆除或增设过鱼设施的优先次序,如鸿景、城北、新中、滩冲水电站对流域整个水系连通性影响较大,可优先考虑拆除或增设过鱼设施。
5 结语
伴随着城镇化进程的加速,大量的水电站建设对水系连通性造成了很大的影响,给流域水环境、水生态造成了不可逆的不利影响。本文采用VCI法、阻隔系数法、改进阻隔系数法定量评估水电站建设对南山河流域河流纵向连通性的影响,同时结合DCI法分析每个水电站对流域水系连通性的影响程度,给出水电站拆除的优先次序,为恢复南山河流域水系连通性提供一种参考,主要得出以下结论。
a)改进阻隔系数法在保持传统阻隔系数法简单、计算快捷优势的基础上,可充分考虑水电站数量、工程类型和所在位置对河流带来的阻隔影响,采用该方法进行河流水系连通性评估更加科学合理。
b)在城镇化建设进程中,水电站(尤其是未建过鱼设施的中小型水电站)建设将大幅降低流域水系的连通性,对水系连通性产生显著的不利影响;与此同时,相比大型流域,中小型流域的水系连通性受水电站建设的影响更为显著,因此应更加重视中小型流域的水系连通性研究。
c)树状水系连通性指数评估法通过定量分析每个水电站对水系连通性的影响,可以此确定水电站拆除的优先次序来提升整个水系的连通性,为流域水系连通性恢复提供一种科学参考。

