雨量异常数据的空间维度分析与甄别
高月明,林清华,柳树票,徐朝阳
(广东华南水电高新技术开发有限公司,广东 广州 510610)
雨量异常数据是雨量站自动测报的非自然、不真实的雨量,如偏大或偏小。由于设备或操作等因素,自动测报的雨量不可避免地含有异常数据,可能引发错误预警,为灾害防范工作带来困扰。雨量站数量巨大,自动测报频繁,绝大多数无人值守,使得人工校验雨量成为不可能。因此,应用有效方法实时检测并自动过滤异常雨量是非常必要的。
目前,国内外已有较多用于检测雨量异常数据的方法,比较常见的有基于规则、统计和机器学习的方法。
基于规则的方法从业务知识或专家经验中总结异常雨量的匹配规则。例如极值检测方法规定雨量的正常范围,判定范围之外的雨量为异常[1-2];缺测检测方法计算雨量站缺失测量值的次数或时长,判定缺测过多的雨量为异常[2];连续无变化检测方法判定长时间保持某一数值的雨量为异常[2];内部一致检测方法判定与相关气象、设备状态和遥感等要素不一致的雨量为异常[3-4]。基于规则的方法能够快速而准确地找出符合规则的异常雨量,但可能会受限于不完善的规则库无法周到照顾各种特殊情况。
基于统计的方法运用统计学理论探究雨量统计分布或建立预测模型。例如箱形图、拉依达准则(PauTa’s Criterion)、肖维勒准则(Chauvenet’s Criterion)、格拉布斯检验(Grubbs’ Test)和迪克逊检验(Dixon’s Q Test)等检测方法判定足够远离样本分布主体的雨量为异常[5-8]。线性或广义线性模型、马尔可夫随机场(Markov Random Field)等模型预测雨量,判定与预测值有显著残差的雨量为异常[7,9]。基于统计的方法能够综合考虑数据整体,但也因此容易被边缘数据撬动。如果数据不全、数据偏离总体或异常数据占比较大,统计分布或预测模型就不能准确反映真实情况。
基于机器学习的方法通过监督学习、半监督学习或无监督学习等算法模型对雨量进行分类、聚类或预测。例如变分自动编码器(Variational Auto Encoder)输入雨量和多元气象要素,生成雨量异常的概率分数,判定分数超过阈值的雨量为异常[10]。类似于统计预测,机器学习模型也预测雨量,判定与预测值有显著残差的雨量为异常[11-12]。此类方法灵活性高,拥有很强的学习能力和自适应性,但模型所学到的内容很大程度上取决于数据集,如监督学习要投入大量精力标注数据。如果用于建模的数据集不具有代表性,那么所建立的模型泛化能力就不会太高。
目前,各类方法主要应用在时间维度上,针对单一雨量站的雨量时间序列,解释雨量的趋势和周期性变化,而在空间维度相邻的雨量站可以相互验证同时刻雨量的剧烈变化[13-14]。本文以广东省内5 967座雨量站实测雨量为依据,探究雨量在空间平面上的相关性,将拉依达准则、肖维勒准则、格拉布斯检验和狄克逊检验4种统计方法运用到空间维度对比分析,以期找到一种准确过滤异常雨量的方法,为防汛预警部门提供有效的技术支持。
1 数据
数据来源于广东省5 967座雨量站(图1),包含2022-6-18 4:30、2022-6-21 4:00、2022-6-21 7:45、2022-6-21 8:45和2022-6-21 10:00等5个时刻的15 min雨量记录。因部分雨量站损坏、维护等造成数据缺测,上述5个时刻雨量分别有4 889、4 794、4 840、4 804、4 995条,共计24 322条雨量记录。每条雨量记录包含测站编码、测站名称、东经、北纬、时间和雨量等变量,见表1。
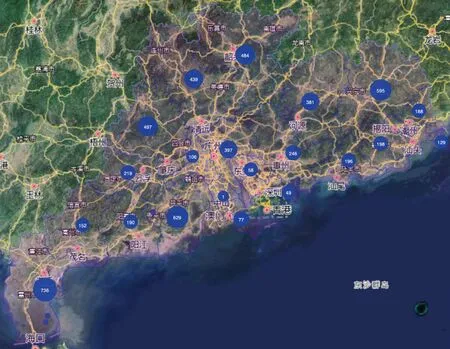
图1 广东省雨量站地理信息
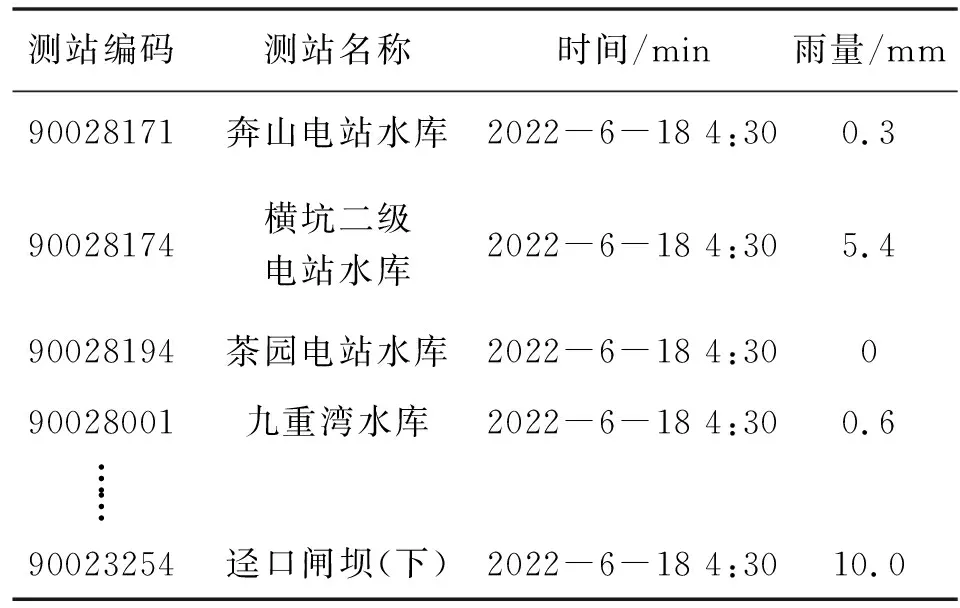
表1 15分钟雨量示例
与小时整点雨量相比,15分钟雨量粒度更小,容易发现细微差异,减少漏掉长时段里不同雨量站的实时雨量存在较大差异而累计雨量却相近的情况。雨量时间序列的变化相当剧烈(图2)。单从时间维度完全解释短时雨量的趋势和变化是十分困难的。
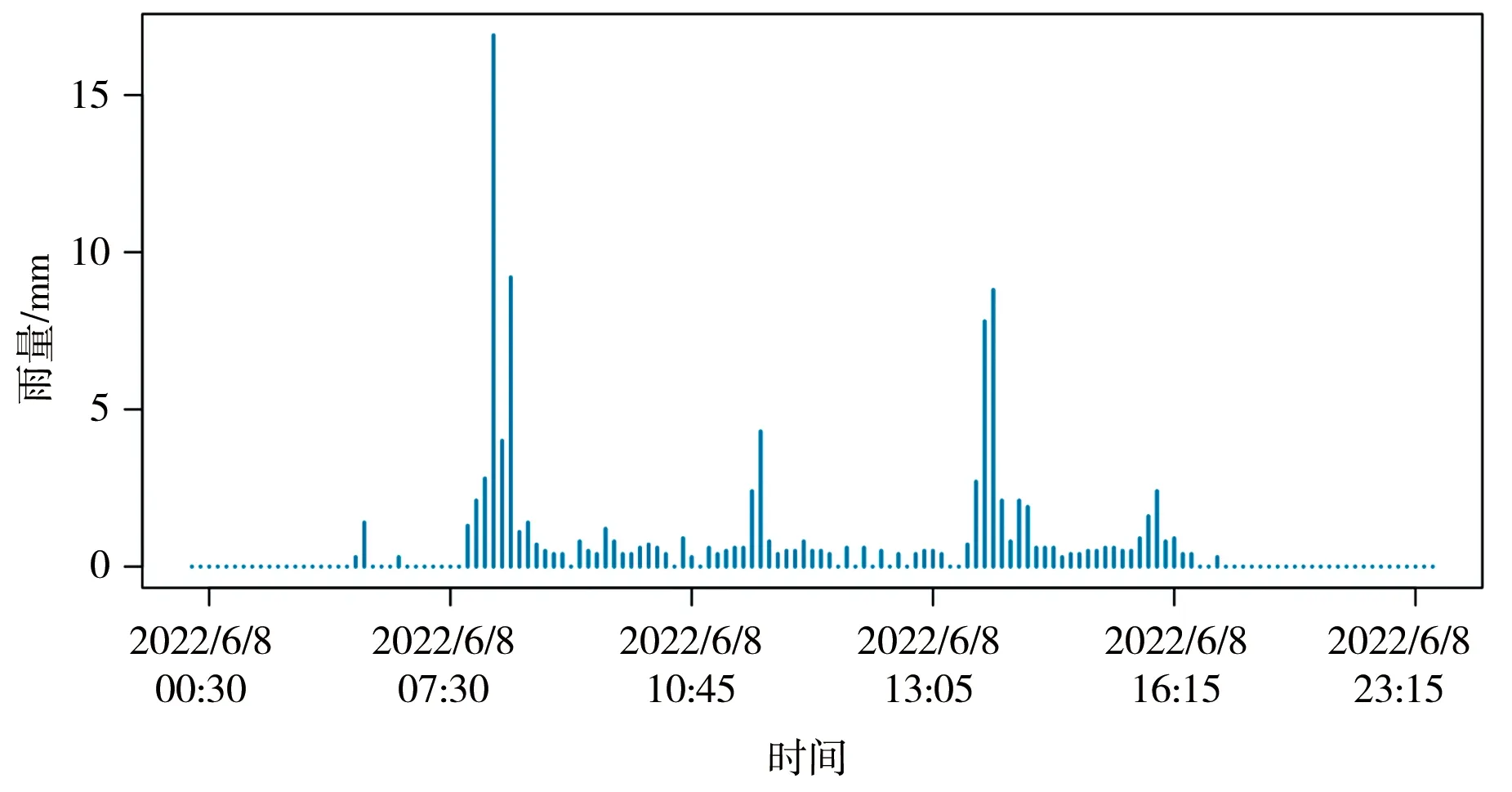
图2 青年水库雨量时间序列
2 方法
方法包括区域划分和假设检验等统计方法。区域划分针对某中心雨量站将其周边的雨量站划分到该中心雨量站的分组。统计方法推断该中心雨量站某时刻雨量在其组内是否异常。
2.1 区域划分
区域划分利用经纬度坐标和测地线计算雨量站之间的距离,针对某中心雨量站将与其相距特定范围内的雨量站划分到该中心雨量站的分组。分组可重叠,即每座雨量站既是自己分组的中心雨量站,也可能是其他一组或多组的周边雨量站。
区域划分的关键是选择合适的距离阈值,为此选择广东省内相距20 km以内的关联雨量站,筛选出两雨量站相同时段有雨的雨量,计算其皮尔逊相关系数,探究相邻雨量站雨量相关程度与其距离的关系。假设两雨量站各有n条对应雨量,相关系数公式如下:
(1)
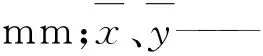
相邻雨量站雨量相关程度随其距离的变化见图3,雨量相关程度随距离变远而大致呈下降趋势,且趋势慢慢减弱,点逐渐发散。两雨量站距离越近其雨量相关程度越强,距离越远其雨量相关程度越弱,但也存在少数不符合认知的特殊情况,如距离非常近的雨量站其雨量却几乎不相关,或者距离非常远的雨量站其雨量却高度相关,甚至还有高度负相关。特殊情况可能包含异常雨量,也可能是由复杂的环境因素造成的,如地形。高山相隔的雨量站即使距离近,其降雨规律也会非常不同。
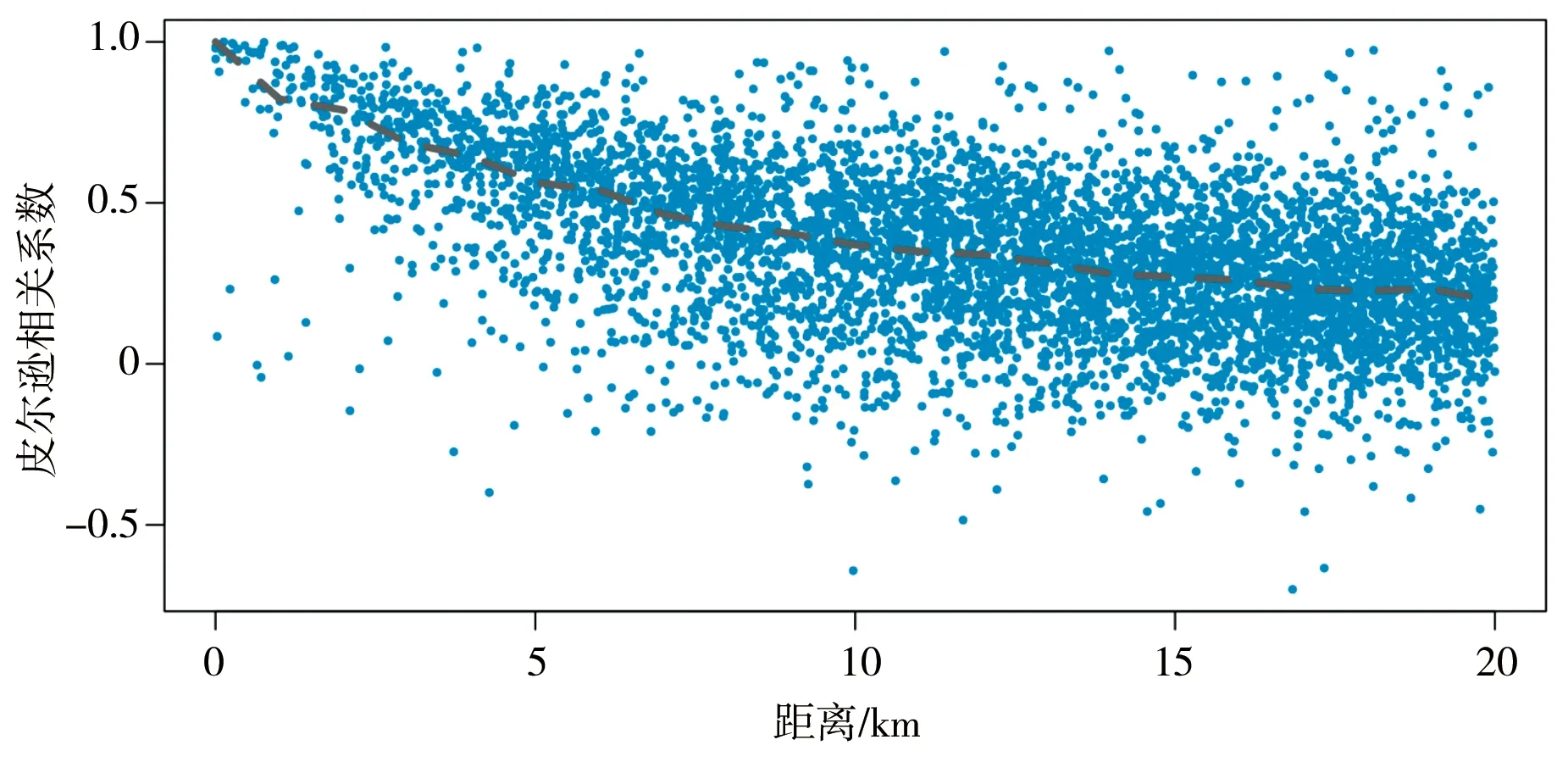
图3 雨量相关程度与雨量站之间距离的关系
综合考虑上述关系和雨量站密度,区域划分选择10 km作为距离阈值,针对某中心雨量站将与其相距10 km以内的雨量站划分到该中心雨量站的分组,图4所示圆圈是以下洋水库雨量站为中心的分组。
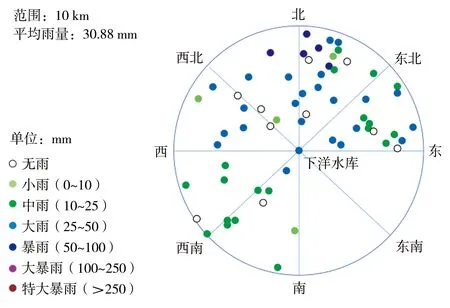
图4 下洋水库周边24 h雨量分布
2.2 统计推断
假设上述划分的某区域中有n座雨量站,其某时刻的雨量样本,可以利用拉依达准则、肖维勒准则、格拉布斯检验和狄克逊检验判断某雨量站的雨量在其区域内是否异常。对于一维的雨量,异常数据通常为离群点,表现为远离样本总体的极值。
2.2.1拉依达准则
拉依达准则通过离群点与样本均值的差值判断该离群点是否异常,是应用最普遍的一种异常数据检测方法,适用于较大样本(一般不低于10)。它计算中心雨量站的雨量与样本均值的差值和样本标准差:
(2)
(3)
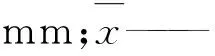
如果差值D大于3s,则可疑值被认定为异常[15-16]。
2.2.2肖维勒准则
肖维勒准则同样通过离群点与样本均值的差值判断该离群点是否异常,但增加考虑样本容量。如果差值D>ws,则可疑值被认定为异常。其中,w为肖维勒准则的系数,对应不同的样本容量。根据肖维勒准则,当样本容量为200时,肖维勒准则系数为3,拉依达准则才有效[15,17]。
2.2.3格拉布斯检验
格拉布斯检验通过衡量离群点远离样本均值的程度来判断该离群点是否异常,通过式(4)—(6)计算检验统计量G:
(4)
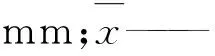
上限检验统计量G为:
(5)
式中xmax——区域中的最大雨量,mm。
下限检验统计量G为:
(6)
式中xmin——区域中的最小雨量,mm。
上限检验统计量用来检验区域中的最大雨量是否异常,而下限检验统计量用来检验区域中的最小雨量是否异常。如果计算得到的统计量大于格拉布斯检验的临界值,则可疑值被认定为异常。临界值与样本容量和置信度对应。置信度α表示将不拒绝(1-α)%的数据,即对判定的异常有(1-α)%的自信[15,18-19]。
2.2.4狄克逊检验
狄克逊检验通过衡量离群点远离样本群体的程度来判断该离群点是否异常,适用于较小样本(一般不超过30)。它按照升序排列雨量样本,通过式(7)计算检验统计量Q:
(7)
式中xc——中心雨量站的雨量,mm;xa——升序排列中与xc最近的雨量,mm;xmax——区域中的最大雨量,mm;xmin——区域中的最小雨量,mm。
狄克逊检验统计量的计算公式在不同样本容量上也有区别(表2)。类似格拉布斯检验,上限检验统计量用来检验区域中的最大雨量是否异常,而下限检验统计量用来检验区域中的最小雨量是否异常。如果计算得到的统计量大于狄克逊检验的临界值,则可疑值被认定为异常。临界值同样与样本容量和置信度对应[20-21]。
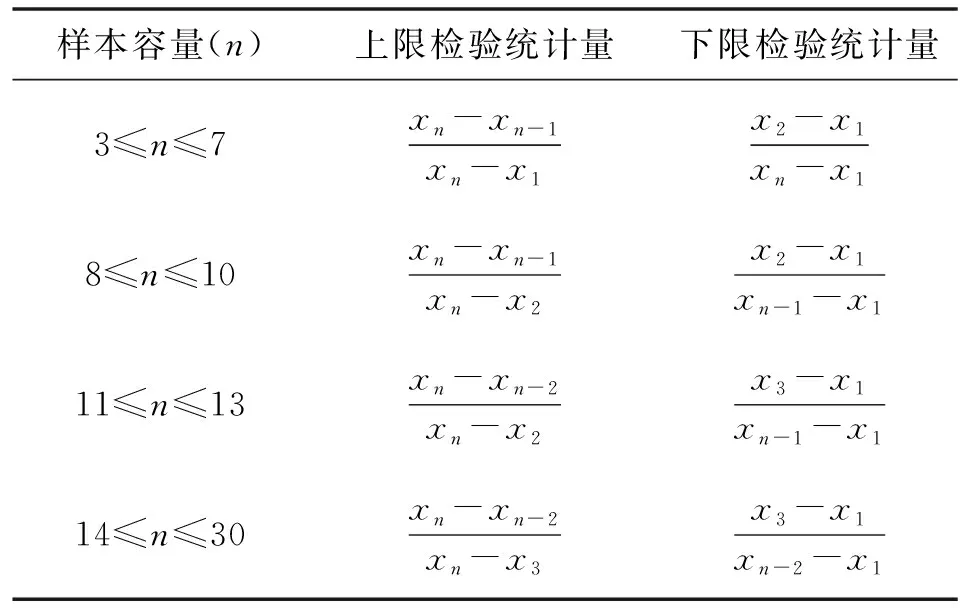
表2 样本容量与狄克逊检验统计量公式对应
3 结果
3.1 区域分组表现
24 322条雨量记录对应24 322个分组,除去经纬度为0、雨量站少于3座等无效分组,剩余23 228个分组。每组平均包含15.96座雨量站,组内周边雨量站平均距离其中心雨量站6.33 km。雨量站数量分布和各雨量站到其中心雨量站距离分布见图5。
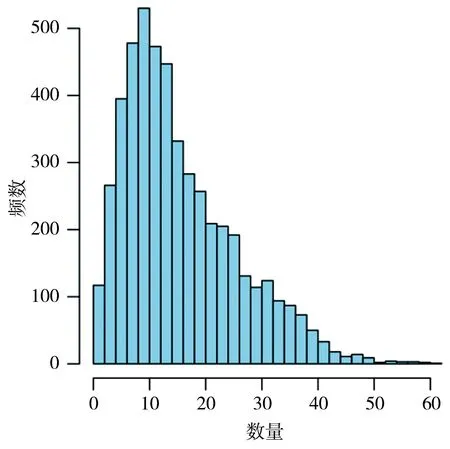
a)分组雨量站数量分布
假设当半径为10 km的圆形区域内普遍降雨时,其雨量也近似服从正态分布,但左侧被0截断。夏皮洛-威尔克检验(Shapiro-Wilk Test),简称S-W检验,对雨量进行正态性检验,统计量接近1,P值大于0.05,表示雨量样本来自正态分布[22]。经过检验,79%(18 246/23 228)分组的区域雨量能通过S-W检验(表3)。
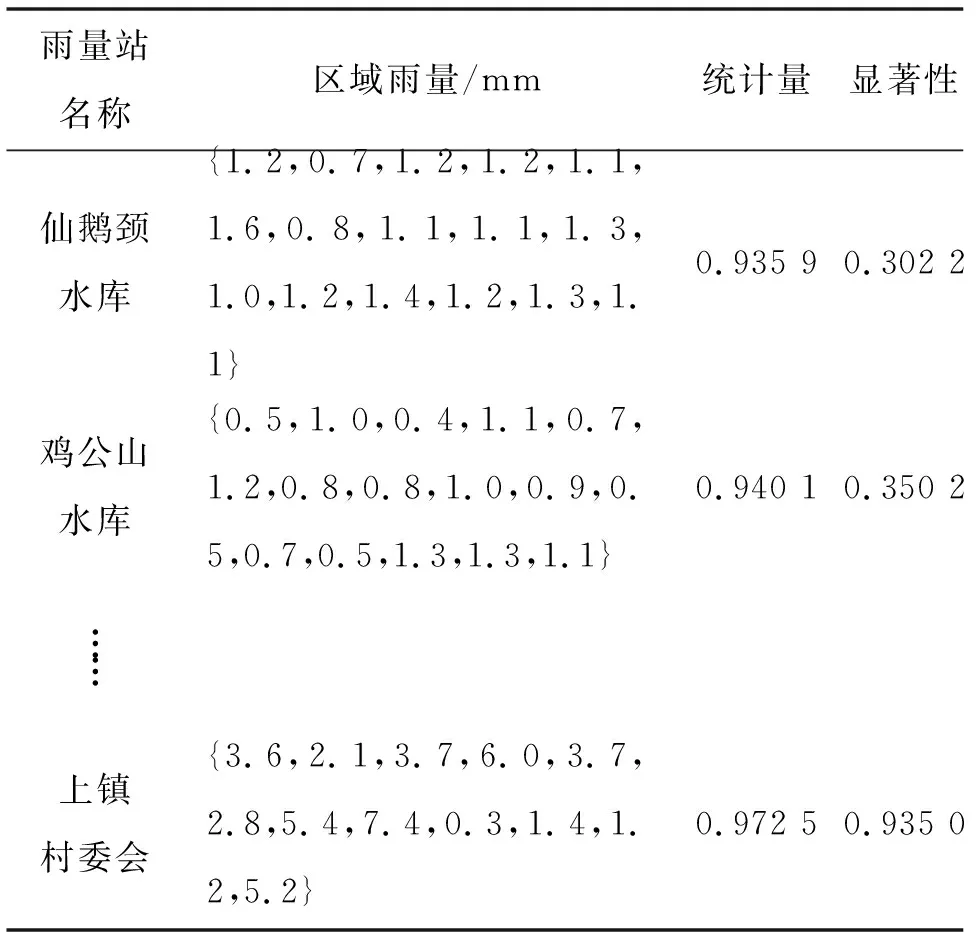
表3 区域雨量S-W检验
3.2 统计方法对比
4种统计方法推断23 228个分组的区域雨量的报错率(预测阳性数量/数据数量)分别为0.33%、1.08%、0.96%和0.91%。对比测试过程分别用4种方法区分236条正样本和472条负样本,得到混淆矩阵,见表4—7。

表5 肖维勒准则的混淆矩阵

表6 格拉布斯检验的混淆矩阵
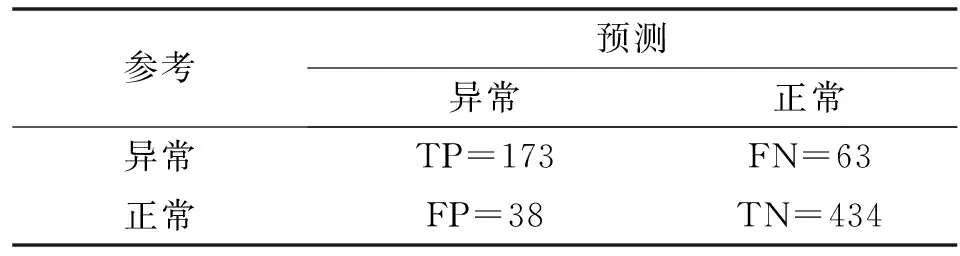
表7 狄克逊检验的混淆矩阵
拉依达准则判定雨量异常的条件非常宽松,是真阳性和假阳性(第二类错误)最少的,也是真阴性和假阴性(第一类错误)最多的,仅将2例真实正常雨量辨别成了异常雨量,却放过了大量的真实异常雨量;另外3种方法的结果十分相似,但值得注意的是,肖维勒准则判定雨量异常的条件最严厉,是真阳性和假阳性最多的,也是真阴性和假阴性最少的;然后依次是格拉布斯检验和狄克逊检验条件相对宽松一点,可能与置信度的选择有关,但更大程度上是受区域划分的分组中异常雨量不唯一影响。
为进一步量化对比4种方法,计算准确率、精确率、召回率和F1分数等衡量方法准确性的指标,见表8。准确率为判断正确的结果占总样本的百分比:
(8)
精确率为预测为正的样本中实际为正样本的百分比:
(9)
召回率为实际为正的样本中被预测为正样本的百分比:
(10)
F1分数被定义为精确率和召回率的调和平均数,是衡量二分类准确性的一种指标:
(11)
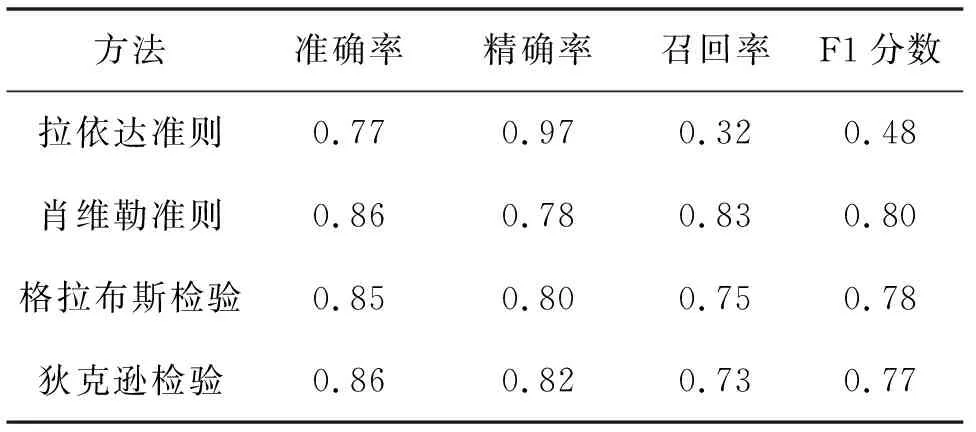
表8 统计推断方法的准确性指标
综合对比4种方法,肖维勒准则表现最好,虽然精确率稍低,但其他各项指标都是相对最好的。当流程多次检测到同一雨量站在不同时刻的雨量异常时,那么判定该雨量站的雨量异常的准确性将大大提高。
3.3 实例分析
雨量野值很少,异常最普遍的原因是雨量计的关键水流通路被异物阻塞,使得承雨器内承接的雨水无法及时流下,造成雨量计读数不准。阻塞影响水流速度,当实际降雨快于承雨器内雨水下渗的速度时,表现为该雨量站读数比周围雨量站读数小。阻塞严重时,测量雨量甚至经常为0,见图6。当实际降雨慢于承雨器内雨水下渗的速度且承雨器内尚存大量积水时,表现为该雨量站读数比周围雨量站读数大,见图7。
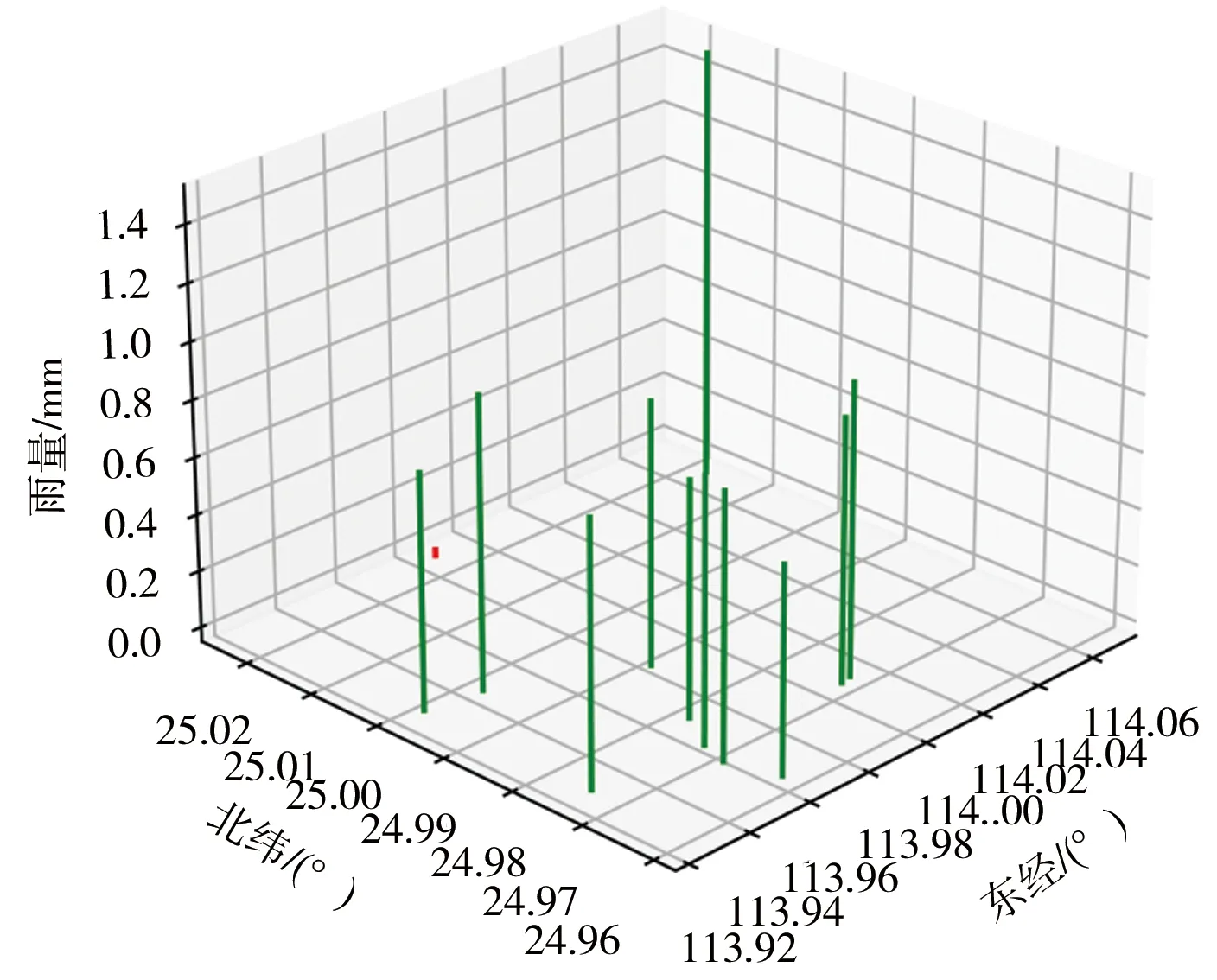
图6 小地水库周边同时段雨量分布
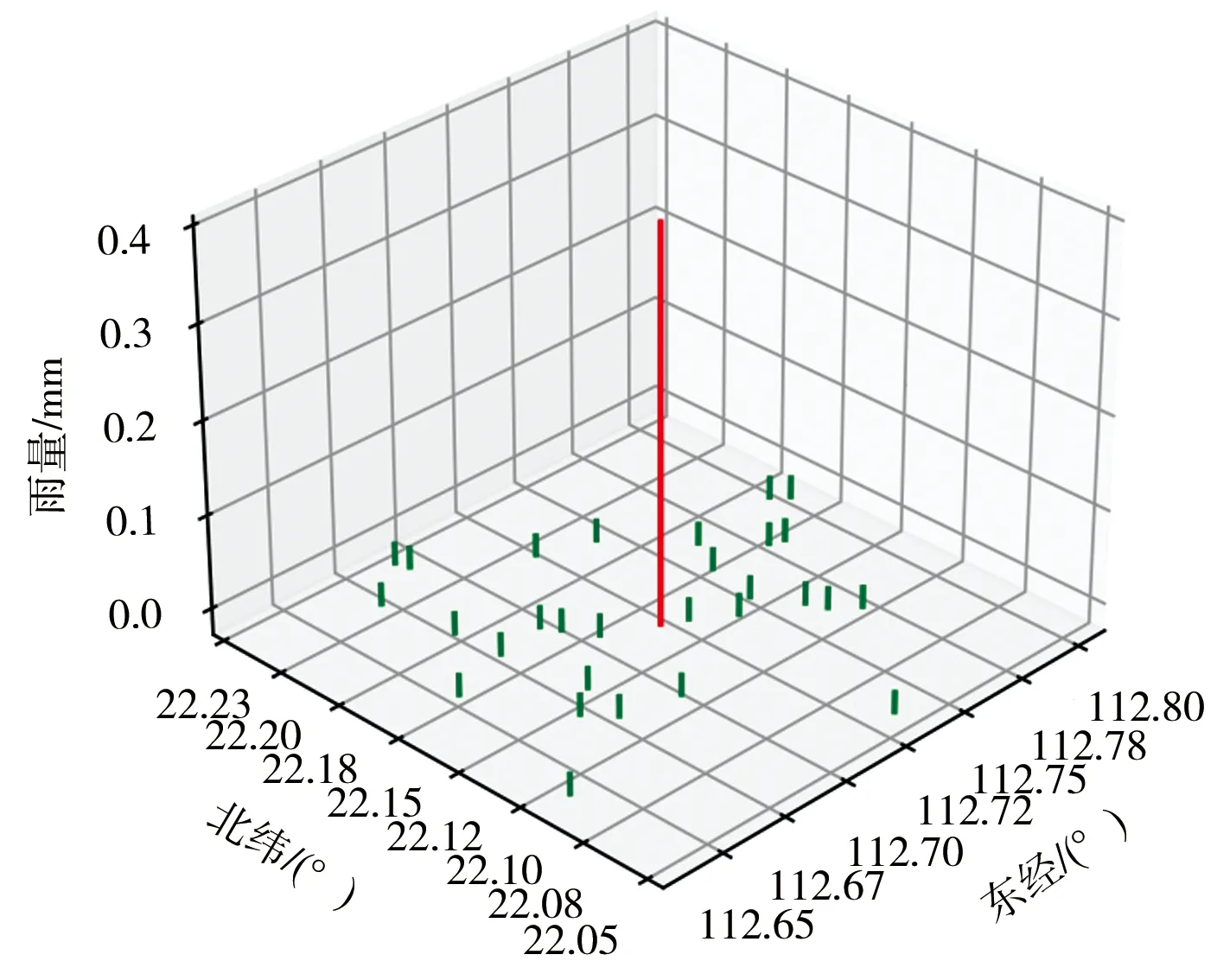
图7 茶亭下水库周边同时段雨量分布
雨水下渗很慢很均匀,使得急促的降雨沿时间平展开来,表现为雨量时间序列很平滑,甚至保持同一读数直到承雨器内所有雨水渗完晒干,见图8、9对比。
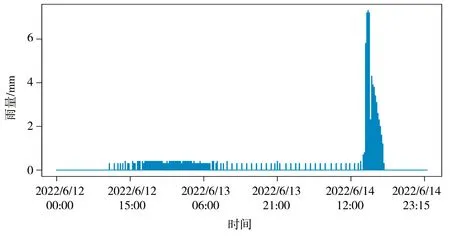
图8 茶亭下水库雨量时间序列(阻塞)
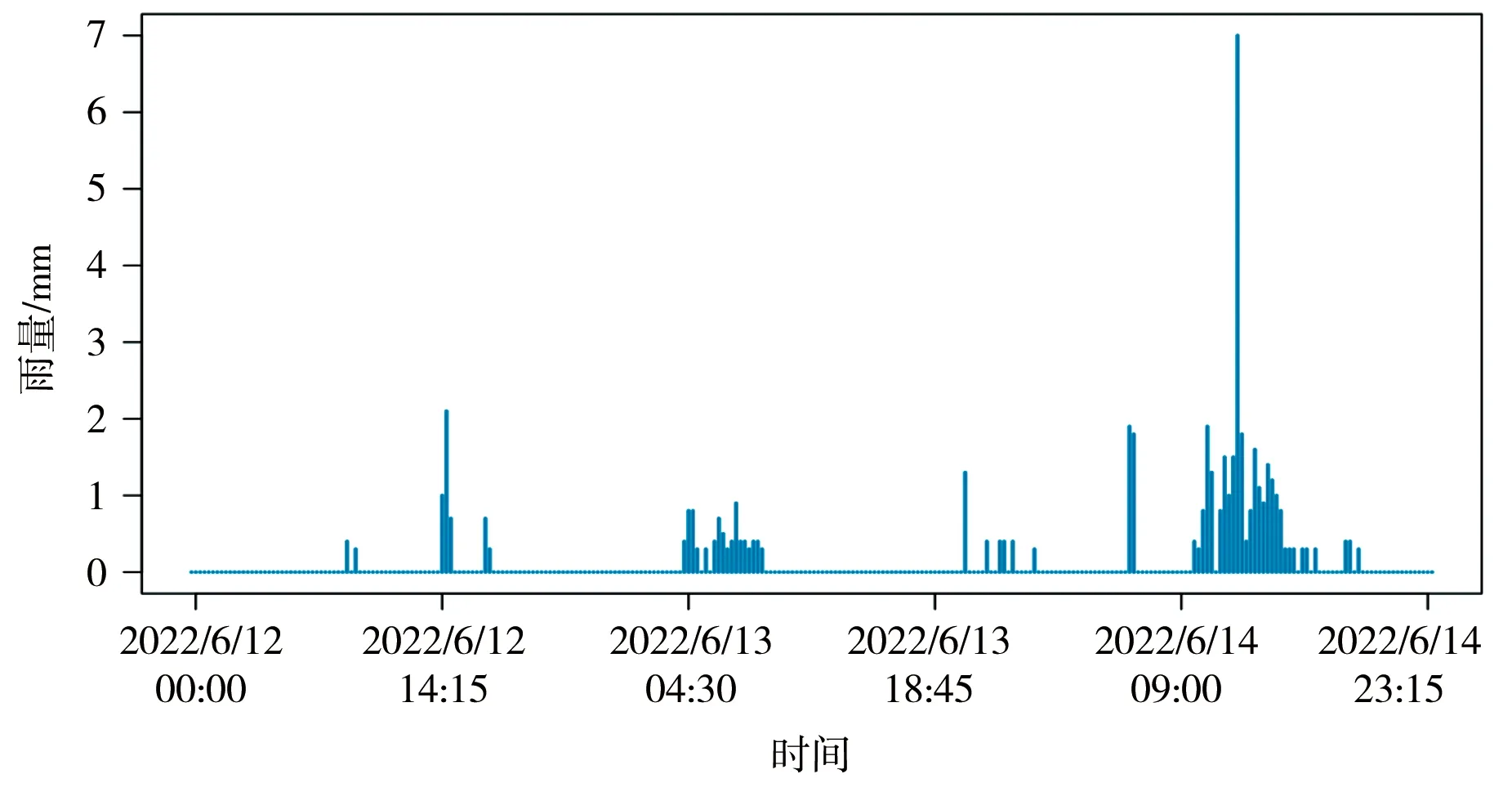
图9 鸡公塘水库雨量时间序列(正常)
4 结论
同时刻雨量在空间分布上具有很高的相关性,其距离越近相关系数越高的规律符合基本生活常识,也为从空间平面判断某点雨量是否异常提供支持。当区域内普遍降雨时,该区域内的雨量近似服从正态分布,为应用统计方法推断异常雨量提供假设依据。对比4种统计方法,各有利弊。拉依达准则过于保守,但却是精确率最高的;格拉布斯检验和狄克逊检验理论上更精妙,但容易被区域分组中多个异常雨量干扰。综合评价肖维勒准则表现最好,简单便捷,且各项指标都相对优秀。需要注意的是在选用拉依达准则时尽量保证区域内雨量站大于等于10座,其他3种方法大于等于3座。事实证明,从空间平面判断某点雨量是否异常是可行的,能够切实帮助水利监管部门提高预警质量,降低人工成本。但该领域方法还有很大进步空间,从数据特征的角度,考虑充分利用时间和空间雨量,同时加入经纬度和距离权重或许能够有更好的效果;从区域划分的角度,距离、地形、气候等因素值得深入探究;从判断方法的角度,运用自适应的人工神经网络等机器学习模型,识别异常雨量的准确性和稳定性定能有全面大幅提升。

