基于无差拍电流预测控制的永磁同步电机谐波电流抑制策略

谷 鑫 鲁金月 王志强 金雪峰 陈 炜

基于无差拍电流预测控制的永磁同步电机谐波电流抑制策略

谷 鑫 鲁金月 王志强 金雪峰 陈 炜

（高效能电机系统智能设计与制造国家地方联合工程研究中心（天津工业大学） 天津 300387）

为解决永磁同步电机在运行过程中三相电流发生畸变、谐波含量高等问题，该文提出一种新的谐波电流抑制方法。首先分析了各次谐波电流在对应同步旋转坐标系下的表现形式，并在此基础之上设计了闭环谐波电流检测系统对谐波电流进行提取，最后采用无差拍电流预测控制策略生成补偿电压用于抑制谐波电流。仿真与实验结果表明，该方法可以有效抑制谐波电流，提高电机三相电流的正弦度，并且具有计算简单、易于实现的特点。

永磁同步电机 谐波电流 谐波抑制 同步旋转坐标系 无差拍电流预测控制

0 引言

永磁同步电机具有功率密度高、运行速度范围广等优点[1-2]。但电机本体电磁结构设计和工艺偏差、电力电子驱动装置的非线性等因素会导致电机定子电流中含有一定量的谐波分量。谐波电流会导致电机的转矩波动，降低系统的运行性能[3-5]。因此，抑制电流谐波对于保证电机系统稳定运行具有重要作用。

目前，针对永磁同步电机定子电流谐波抑制的研究主要从电机电磁结构设计和系统控制算法两个层面展开[6]。电机设计方面通常利用有限元分析优化电机电磁结构，设计适当的转子结构和定子绕组分布来提高电机电势的正弦度，减少由电机本体引起的谐波[7-9]。

系统控制算法方面是通过优化电机控制策略，采用补偿谐波分量的思路对谐波电流进行抑制。本文主要从控制算法的角度针对传统策略中存在的不足，对永磁电机谐波电流抑制算法进一步加以改进。

现有控制方法中谐振控制由于能无静差跟踪正弦交流信号，被应用于谐波抑制中。文献[10-11]将谐振控制器与电流环PI控制器并联，补偿电流环输出电压中的谐波，从而达到抑制电流谐波的目的。文献[12]则在谐振控制器与传统PI控制器并联的基础上，在固定频率下采用离线方式对转子磁链进行识别，形成电流-磁链表，并采用查表法实现控制。文献[13]则是将谐振控制器与PI控制器相串联，谐波电流先经过谐振控制器进行放大，然后与给定值进行比较获得谐波电流误差，最后利用PI控制器对误差进行调节，从而达到抑制谐波电流的目的。文献[14-15]针对电机在弱磁区运行时电流畸变严重、转矩波动大的问题，提出了基于比例-积分谐振控制器的谐波抑制策略，该方法对电流谐波抑制及转矩波动抑制有较好的效果。

文献[16]利用了基波反电动势分量与谐波反电动势分量的幅值比与频率无关的特性来计算补偿电压。此种方法原理简单、易于实现，大大减小了计算难度。文献[17-18]提出了一种利用多同步旋转坐标系的谐波消除方法。将不同阶次的谐波电流变为对应阶次的直流分量，然后经过低通滤波器（Low Pass Filter, LPF）提取出来。各次谐波电流经过PI调节器得到补偿电压。利用多同步旋转坐标系理论可以实现在线提取谐波分量，提高了谐波电流提取结果的准确度。

本文对基于多同步旋转坐标系的谐波补偿方法进行改进，旨在设计一种获得补偿电压更为简单的谐波抑制算法。首先，建立了含有谐波的永磁同步电机数学模型，给出了5、7次同步旋转坐标系下的离散电流预测模型，并采用多同步旋转坐标系与LPF提取谐波电流；为了解决PI控制器获得补偿电压时参数整定复杂以及存在控制延时的问题，本文进一步将多同步旋转坐标系理论与无差拍电流预测控制相结合，补偿电压由无差拍模块计算得出。仿真与实验结果表明，该策略能有效抑制谐波电流，提高永磁同步电机的稳定性。

1 考虑谐波的永磁同步电机数学模型

电机定子三相绕组通常采用星形联结方式，理想条件下绕组对称分布，因此电机反电动势波形呈半波对称，即绕组的反电动势波形不含有偶次谐波，且三相次谐波电流之间互差2p/3。因此，定子谐波电流可以表示为

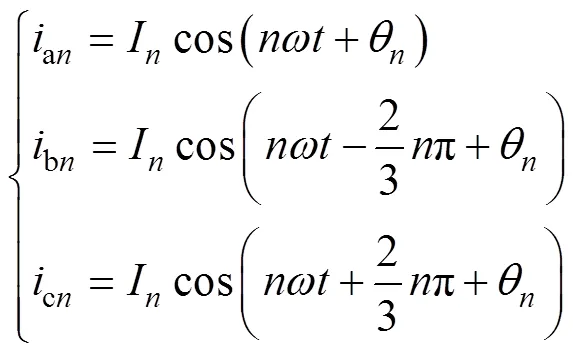
式中，an、bn、cn分别为a、b、c三相次谐波电流；I为次谐波电流幅值；为次谐波电流初始相位；为电机电角速度。

由式（1）可知，当=3（=1, 2, 3,…）时，三相电流中的次谐波电流幅值相等且相位相同。永磁同步电机定子绕组星形联结使3次谐波电流没有导通回路，故在绕组中不存在。当=6+1（=1, 2, 3,…）时，a相电流超前b相电流2p/3、而滞后c相电流2p/3，与基波电流的相序相同，故认为是正序谐波电流。当=6-1（=1,2,3,…）时，a相电流滞后b相电流2p/3、而超前c相电流2p/3，与基波电流相序相反，故认为是负序谐波电流。因此，永磁同步电机三相电流a、b、c的方程可进一步表示为

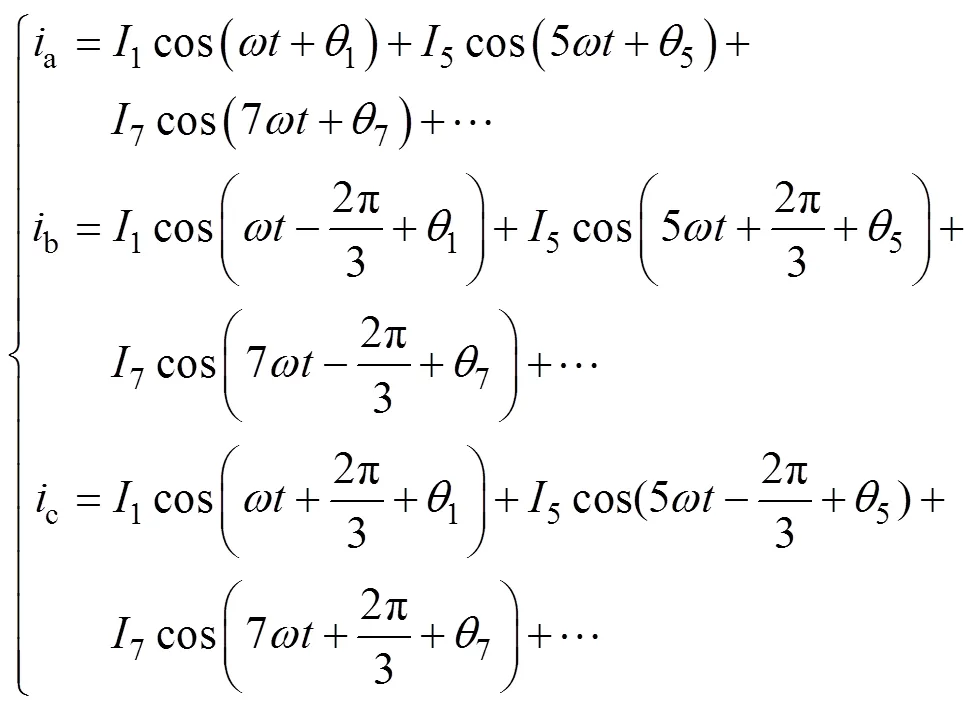
三相静止坐标系变换为两相同步旋转坐标系的变换矩阵为

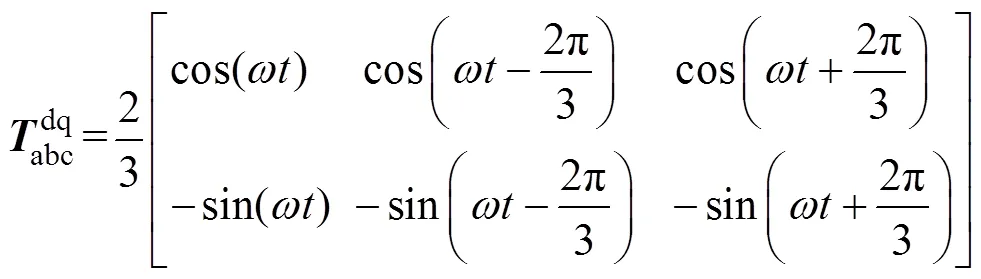
将式（2）经式（3）变换后可得到同步旋转坐标系下的永磁同步电机定子电流表达式为

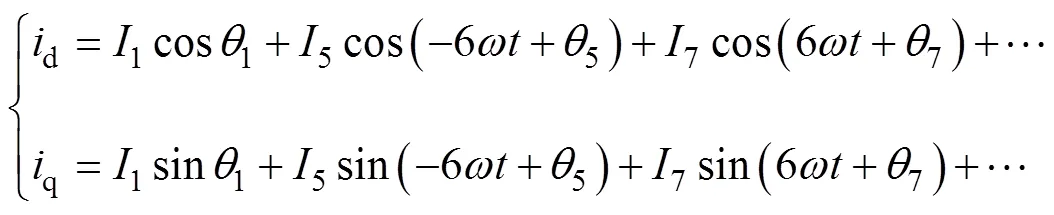
式中，d、q分别为d、q轴定子电流。

在同步旋转坐标系下，电机的电压方程为

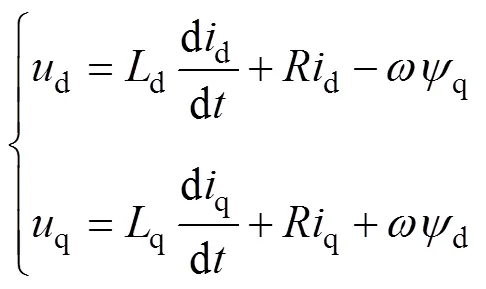
式中，d、q分别为d、q轴定子电压；d和q分别为电机定子的d、q轴电感；为电机定子电阻；d和q分别为定子磁链d、q轴分量。

同步旋转坐标系中考虑谐波的定子磁链为

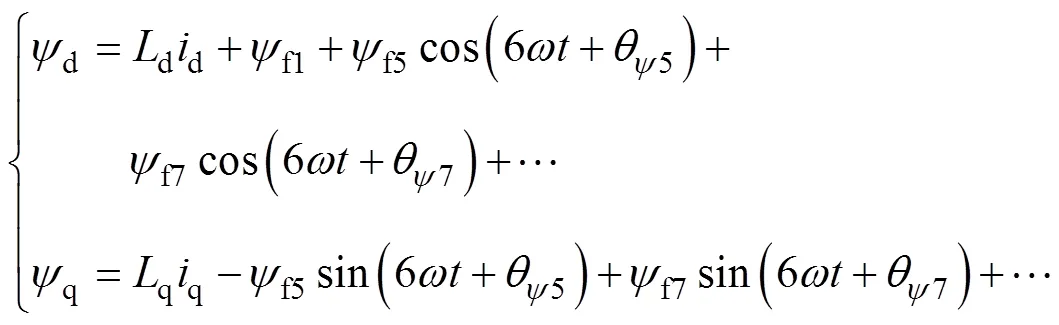
式中，d、q分别为电机定子d、q轴磁链；f1、f5和f7分别为永磁体磁链的基波、5次和7次谐波分量幅值；q5、q7为5、7次谐波磁链的初始相位。

由式（4）和式（6），在同步旋转坐标系下电机的磁链也可以写为

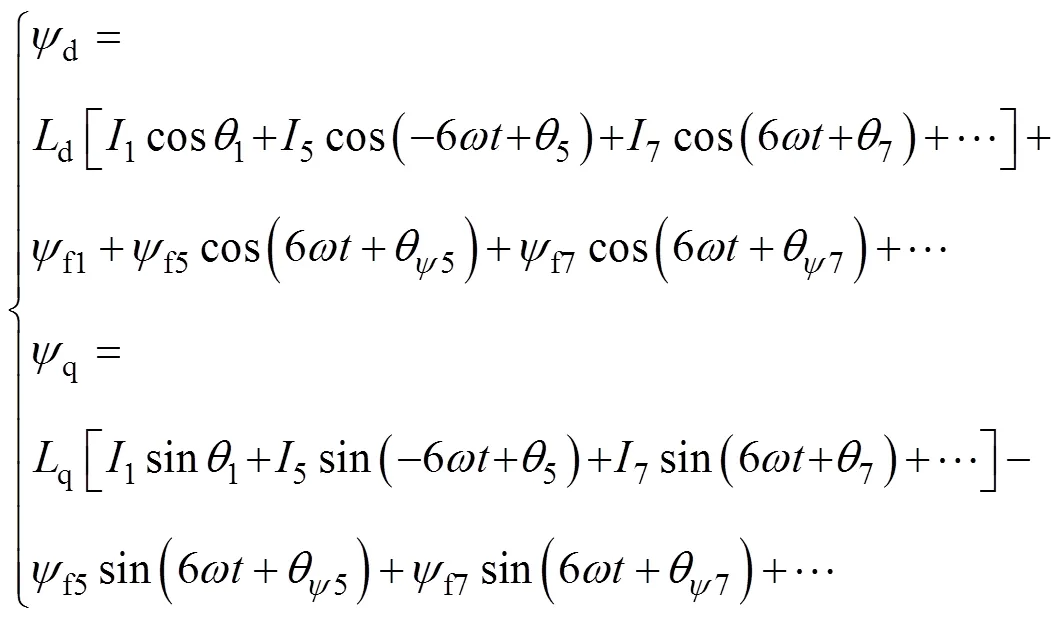
本文主要考虑5、7次谐波电流的抑制，因此忽略更高次谐波。将式（4）和式（7）代入式（5）中可得到含有5、7次谐波的永磁同步电机电压方程为

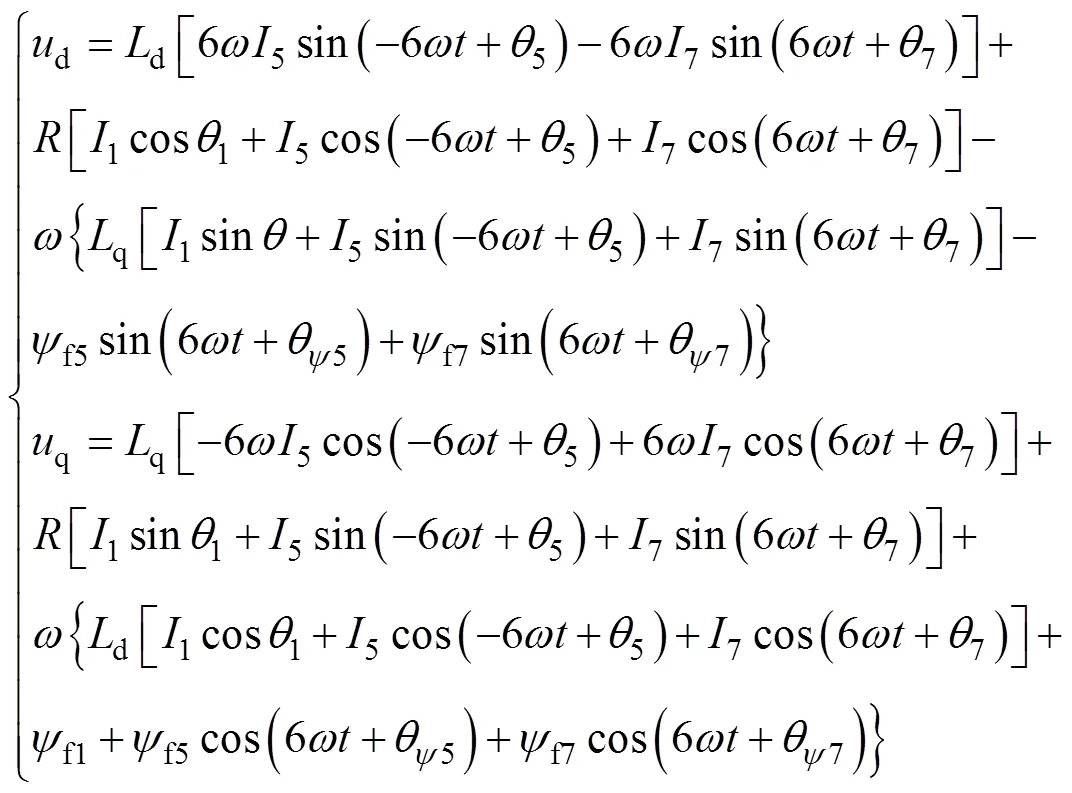
2 电流谐波抑制

2.1 谐波电流检测

由式（2）和式（4）可知，以基波角速度为同步速，经过abc-dq的坐标变换后，d、q轴电流的基波分量为直流量。同理，可以在dq坐标变换的基础上，采用多重同步旋转dq坐标变换法来提取谐波 分量。

基波同步旋转坐标系变换到5次同步旋转坐标系的变换矩阵为

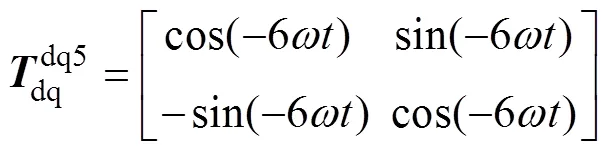
将abc坐标系变换为5次同步旋转坐标系的变换矩阵为

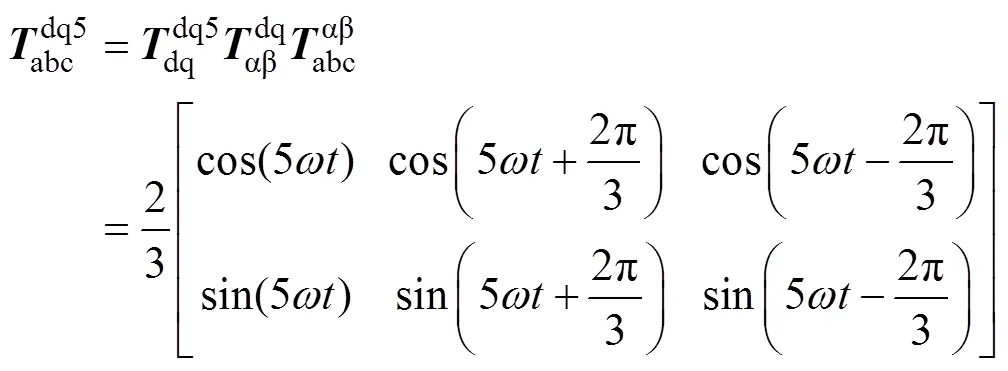
将式（2）经过式（10）变换后可得到电机定子电流在5次同步旋转坐标系下的表达式为

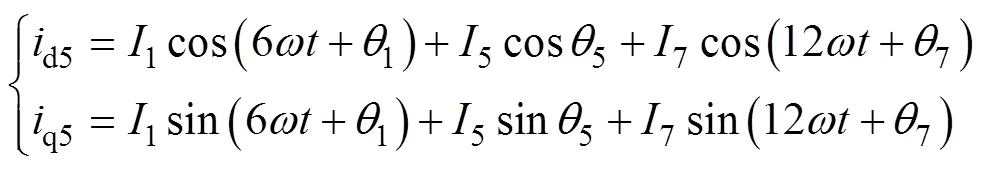
式中，d5、q5分别为定子电流在5次同步旋转坐标系下的d、q轴分量。

基波同步旋转坐标系变换到7次同步旋转坐标系的变换矩阵为

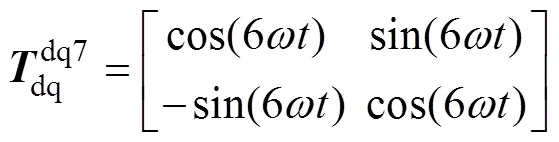
将abc坐标系变换为7次同步旋转坐标系的变换矩阵为

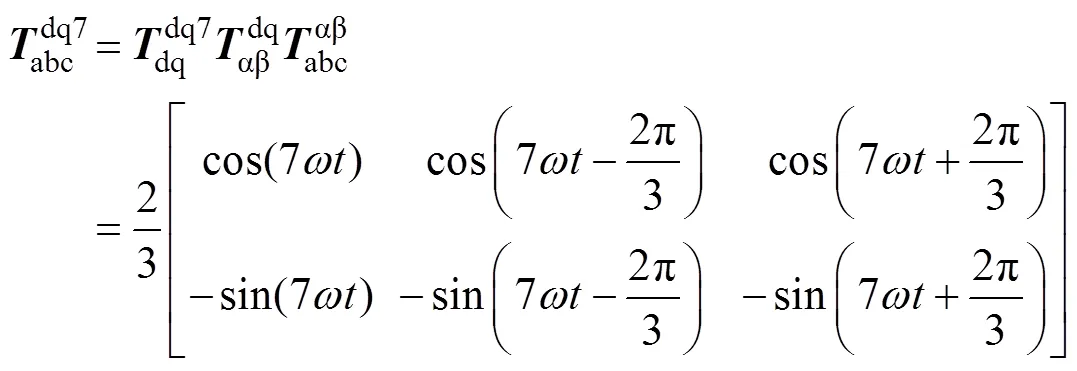
由式（2）和式（13）可得到电机定子电流在7次同步旋转坐标系下的表达式为

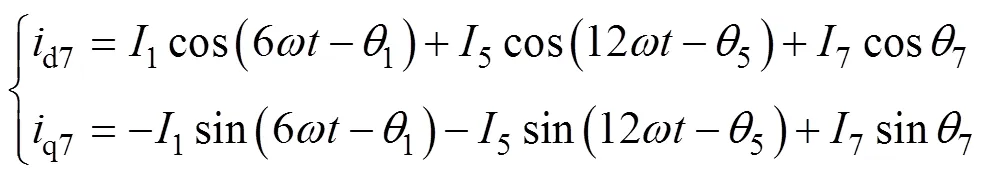
式中，d7、q7分别为定子电流在7次同步旋转坐标系下的d、q轴分量。

由式（11）和式（14）可知，在5次谐波对应的同步旋转坐标系下，5次谐波分量为直流量，基波及其他次数谐波分量为交流分量。在7次谐波对应的同步旋转坐标系下，7次谐波分量为直流量，基波及其他次数谐波分量为交流分量。传统的谐波电流提取方法如图1所示。图中，为电机转子位置角，d5h、q5h分别为5次谐波电流在5次同步旋转坐标系下的d、q轴分量，d7h、q7h分别为7次谐波电流在7次同步旋转坐标系下的d、q轴分量。

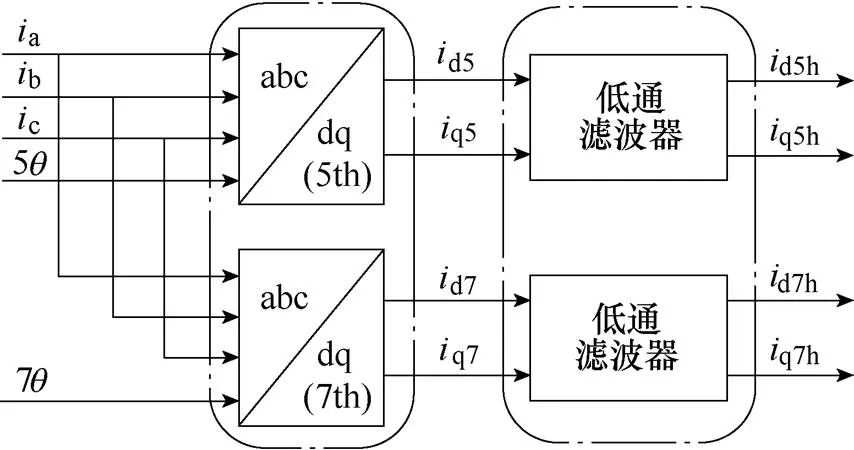
图1 传统的谐波电流提取框图

将电机三相电流变换到5、7次同步旋转坐标系下，经过LPF提取谐波电流。由于LPF一般等效为一阶或以上阶次的惯性环节，导致电流相位产生滞后现象，系统的调节时间较长、动态性能较差。为了能在保证提取谐波电流准确度的同时加快系统的调节速度，保证动态性能，本文采用了一种闭环谐波电流提取（Closed-loop Detection System, CDS）法，因5次和7次提取原理相同，此处仅以提取5次谐波电流为例进行介绍，控制框图如图2所示。

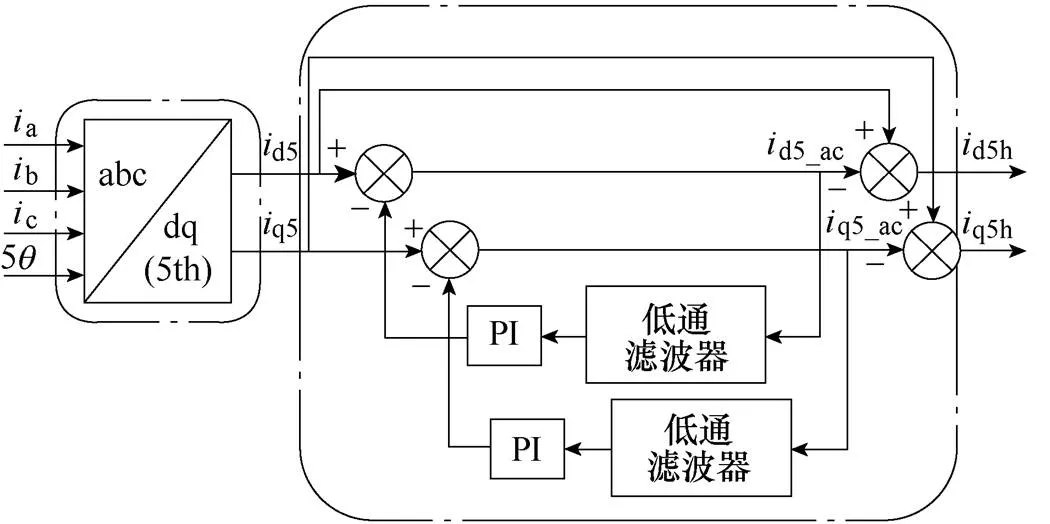
图2 闭环谐波电流提取框图

图2中，dq5既包含直流量也包含交流量，而dq5_ac中只含有交流量，在dq5中减去dq5_ac即可得到5次谐波电流。低通滤波器的阶数为一阶，与传统的谐波电流提取方法相比具有更快的调节速度。

经闭环谐波电流提取模块提取出来的5、7次谐波电流可表示为

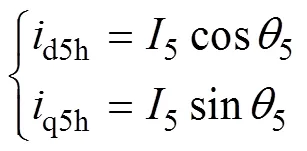
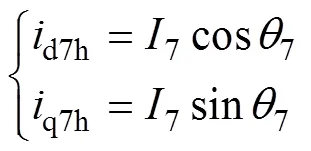
将闭环谐波电流提取框图化简如图3所示。图中，i、o分别为输入量和输出量。

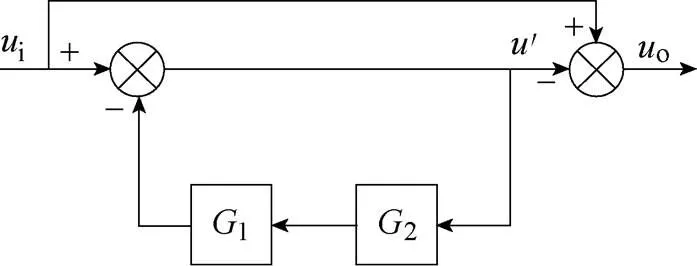
图3 化简后的CDS框图

PI调节器1和一阶低通滤波器2的表达式为

CDS的传递函数可以写为

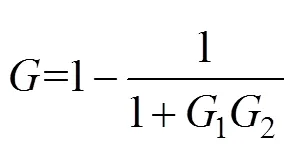
式中，p、i分别为PI控制器的比例系数和积分系数；n为LPF的截止频率。

当i=1，n=5Hz时分别绘制p=0.1、1和20时的伯德图如图4所示。随着p的增加，如p=20时，相频响应曲线在n点的相位滞后比其他曲线更严重。当p较小，如p=0.1时，幅值降为-3dB时的频率为94.58Hz，此时检测的准确度会降低，滤波电流中会含有较多的交流量。

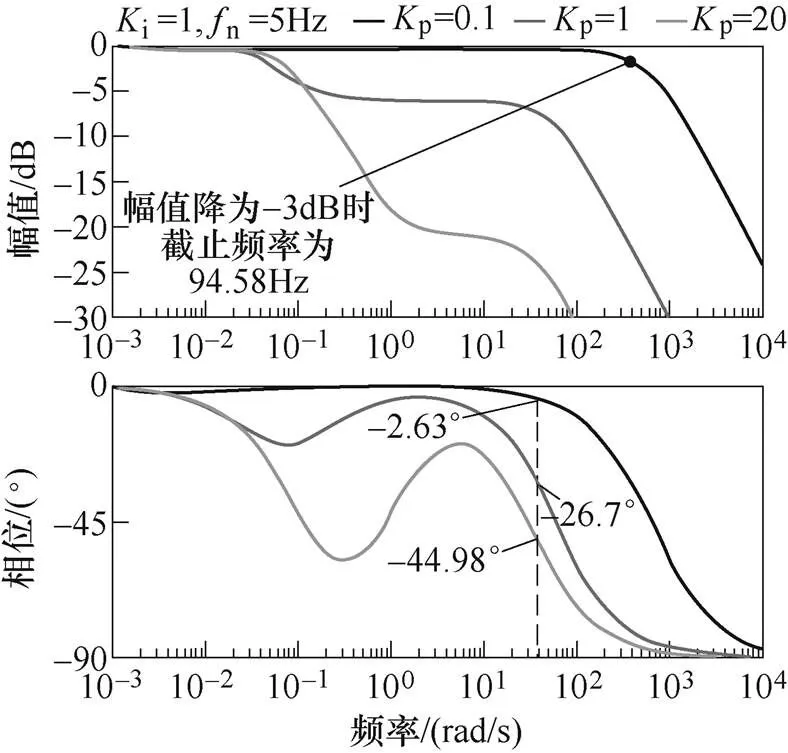
图4 Kp=0.1、1、20时的伯德图

图5为当p=1，n=5Hz，i=0.1、1、20时绘制的伯德图。随着i的增大，n点的滞后相位也会增大，此时会降低谐波检测的精度。

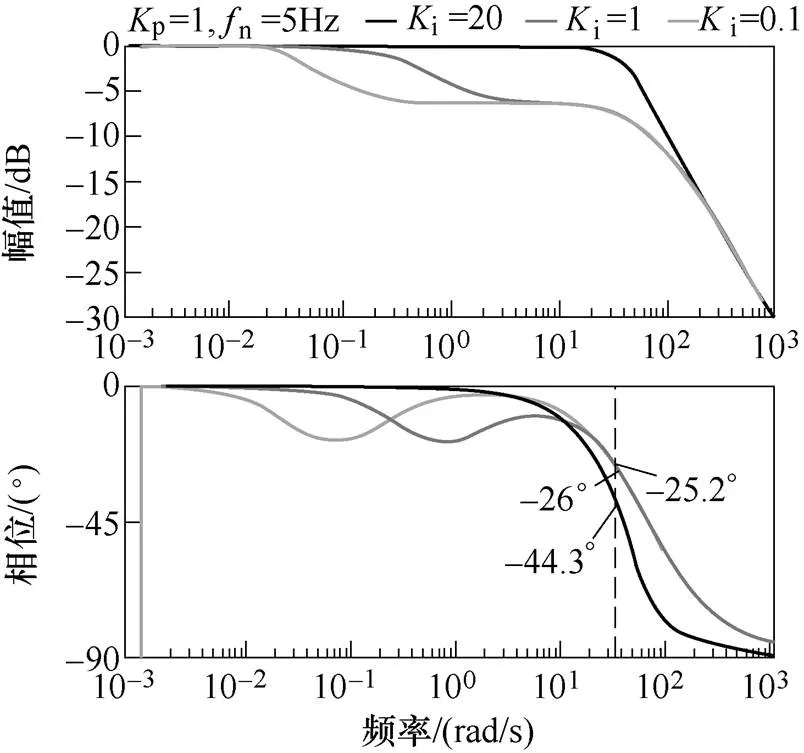
图5 Ki=0.1, 1, 20时的伯德图

图6为当p=2，i=0.1时，n分别为1Hz、5Hz、50Hz时不同方法下伯德图。图中，CDS1和LPF1、CDS2和LPF2、CDS3和LPF3所示曲线分别对应1Hz、5Hz、50Hz时的情况。

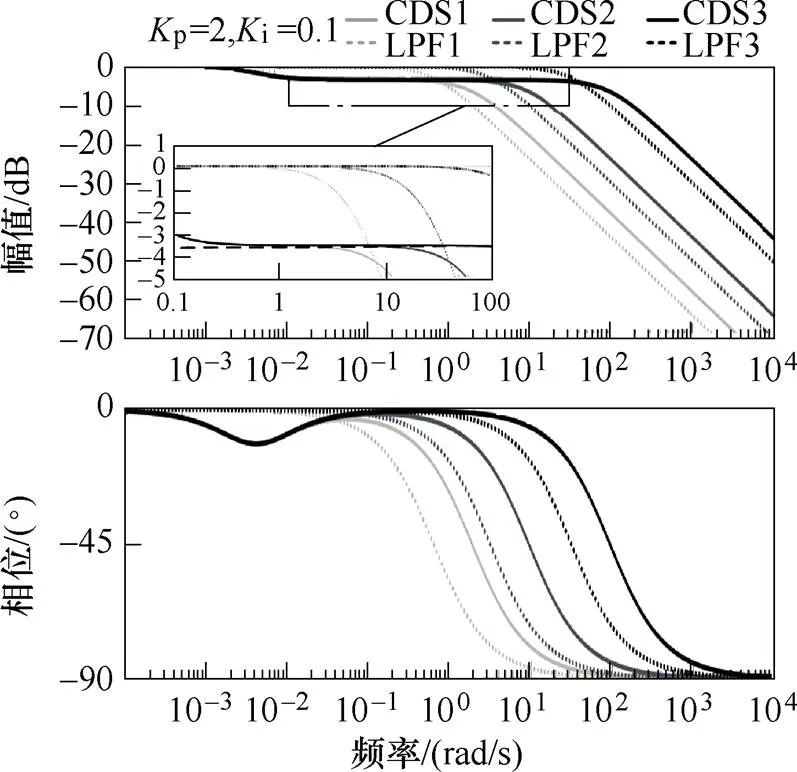
图6 fn=1Hz、5Hz、50Hz时CDS和LPF的伯德图

表1为图6中所示的CDS和LPF的截止频率和滞后相位。c为CDS和LPF幅值分别降为-3dB时的频率，c、n分别为c和n点的滞后相位。

表1 CDS和LPF的截止频率和滞后相位

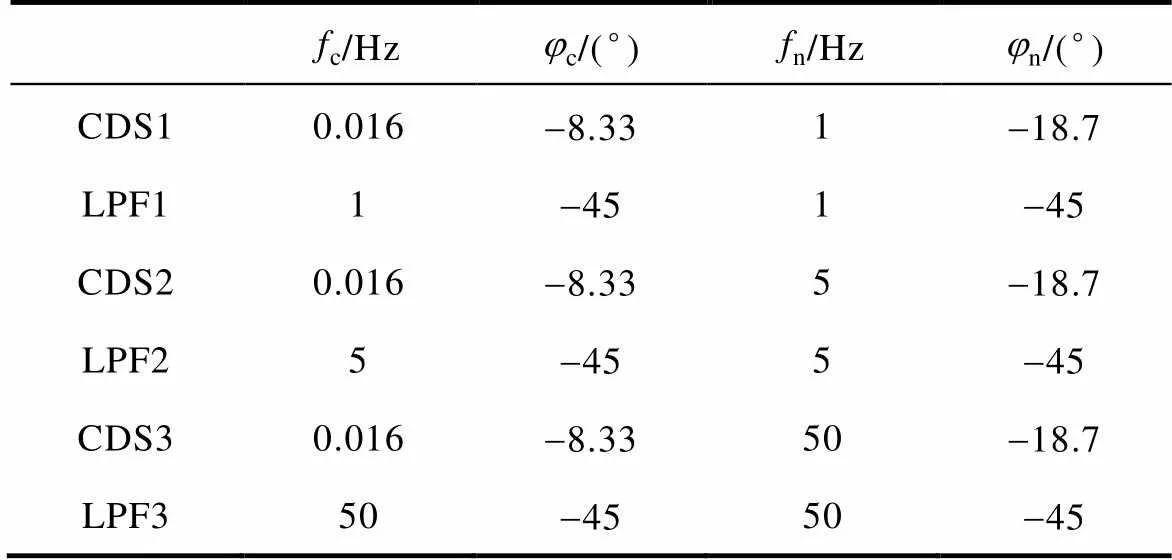
Tab.1 Cutoff frequency and lag phase of CDS and LPF

由图6和表1中数据可知，当幅值降为-3dB时CDS的c小于LPF的c，同时在各n点CDS的幅值均能降为-3.5dB，此时可以更有效地降低交流量。CDS在c和n的滞后角均要小于LPF，可见CDS的谐波提取准确度要更高。

为了使CDS获得更好的性能，本文采用了基于频率响应特性和稳定性分析的参数整定方法，以确定参数p、i以及n。步骤如下：

（1）确定参数范围。随机选取参数初始值，通过分析频响特性初步确定参数p、i以及n的范围。

（2）计算参数。根据分析结果选取特殊点(2pn/100,-3dB)、(2pn/20,-3.5dB)，并将、代入式（19）所示的幅频特性中。

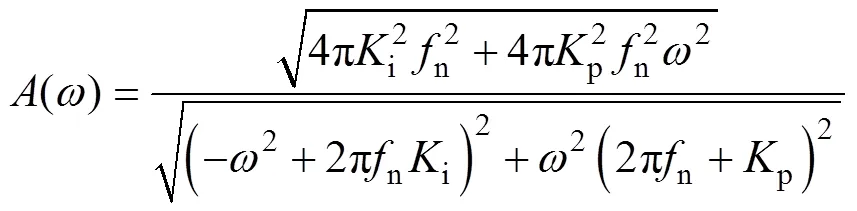
可得

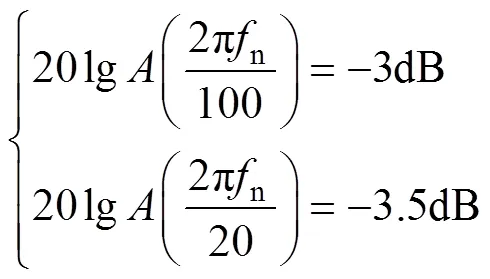
式中，n由经验获得；p、i通过式（19）和式（20）获得。

（3）验证稳定性。根据劳斯稳定性判据，CDS的稳定条件为

（4）将参数代入CDS分析频响特性，如果在2pn/100点幅值大于-3dB，或在2pn/20点幅值大于-3.5dB，则需重新选点计算参数。

2.2 谐波电流抑制算法

在传统的谐波抑制算法中，检测出的谐波电流将经过PI控制器获得补偿电压，如图7所示。图中，dq5h_ref、dq7h_ref分别为5、7次谐波电流的给定值；dq5h、dq7h分别为5、7次补偿电压。

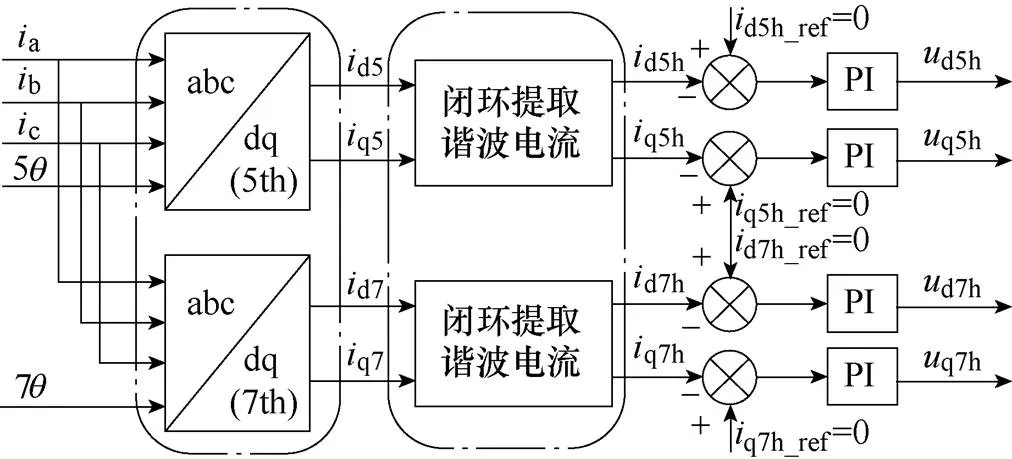
图7 基于PI的谐波电压产生方法

此过程中用到了多个PI控制器，控制器的延时问题所引起的电压误差会影响谐波电流的补偿效果，并且PI控制器的参数整定问题也增加了算法的复杂性。本文提出了基于无差拍预测控制的谐波电压补偿法，其原理如图8所示。5、7次补偿电压由无差拍模块计算得出，不需要用到PI控制器，避免了控制器的延时使产生的补偿电压相位与电机实际谐波电压相位有所偏差的问题，并且节约了调整参数的时间，简化了控制算法。其中5、7谐波电流的给定值均为0。

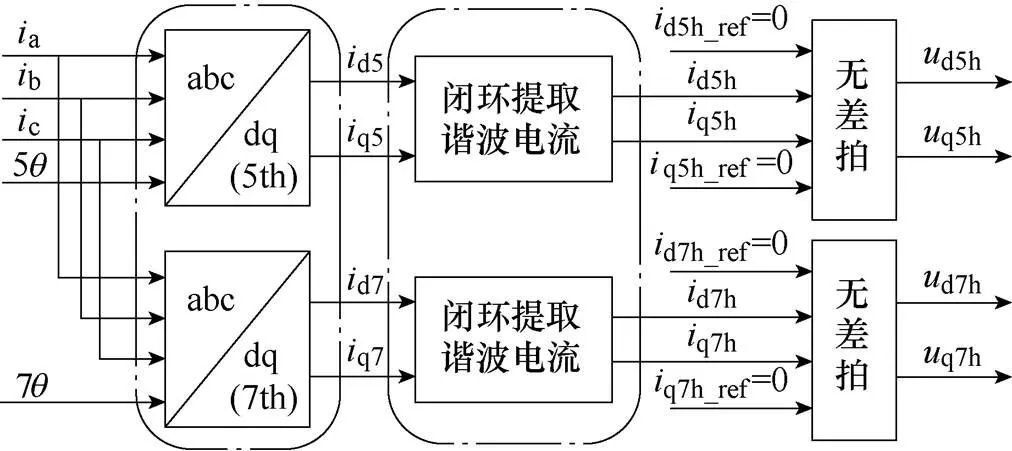
图8 基于无差拍预测控制的谐波电压产生方法

为了抑制第5次和第7次谐波电流，本文分别在5次同步旋转坐标系和7次同步旋转坐标系中建立了电机电流模型。在5次同步旋转坐标系下，经过CDS后的电流状态方程可以表示为

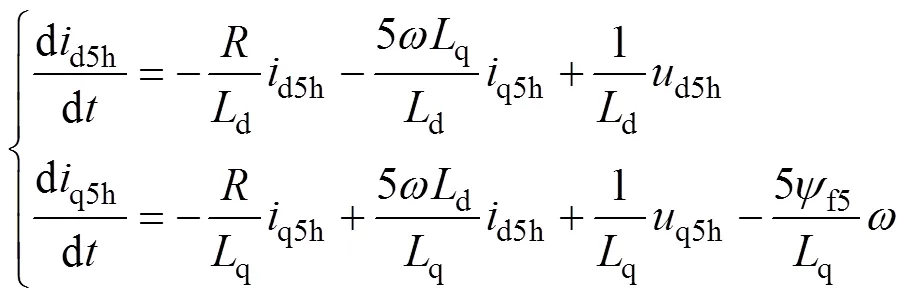
如果电机控制系统的采样周期s足够短，那么永磁同步电机的离散时间模型可以用一阶泰勒级数展开来表示，可近似认为

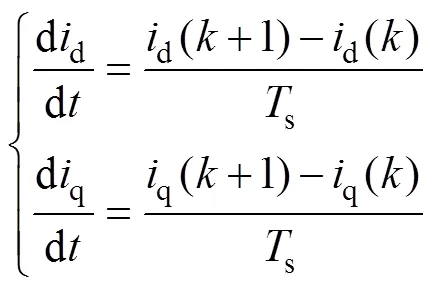
式中，s为电流环采样时间；为采样周期个数；d()q()分别为d、q轴电流在第个采样周期内的值；d(+1)、q(+1)分别为d、q轴电流在第+1个采样周期内的值。将式（23）代入式（22）可得到5次同步旋转坐标系下的离散电流预测模型为

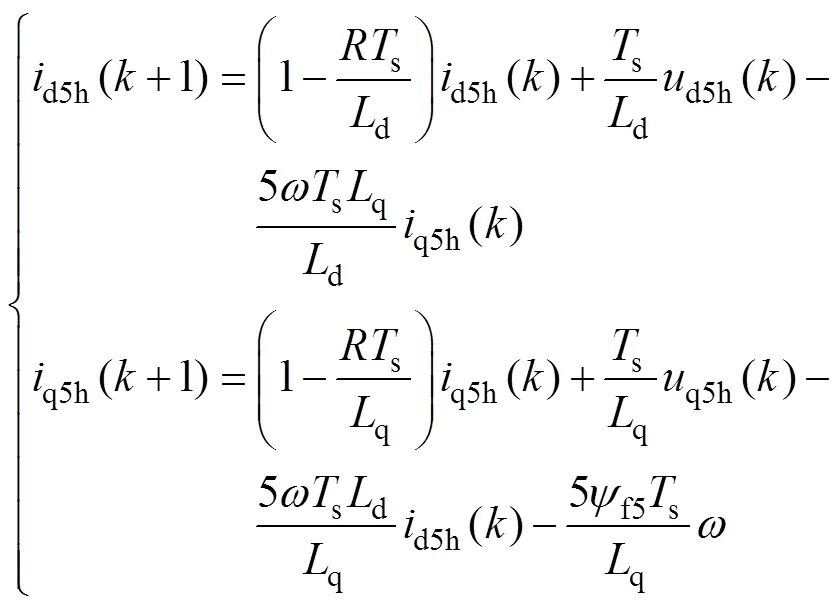
式中，d5h()、q5h()分别为5次d、q轴谐波电流在第个采样周期内的值；d5h(+1)、q5h(+1)分别为5次d、q轴谐波电流在第+1个采样周期内的值；d5h()q5h()分别为5次d、q轴谐波电压在第个采样周期内的值；同理，可得在7次同步旋转坐标系下，经过CDS后的电流状态方程和离散电流预测模型为

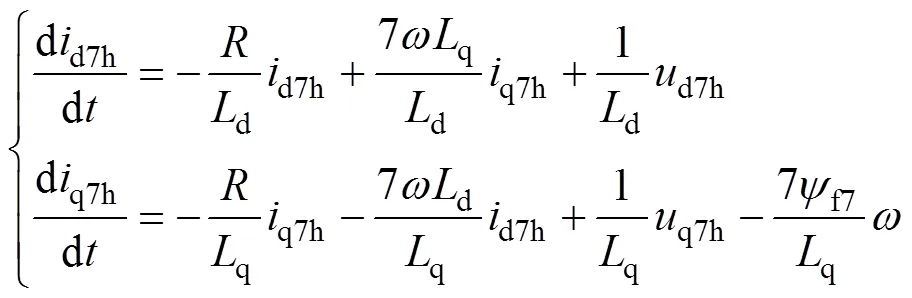
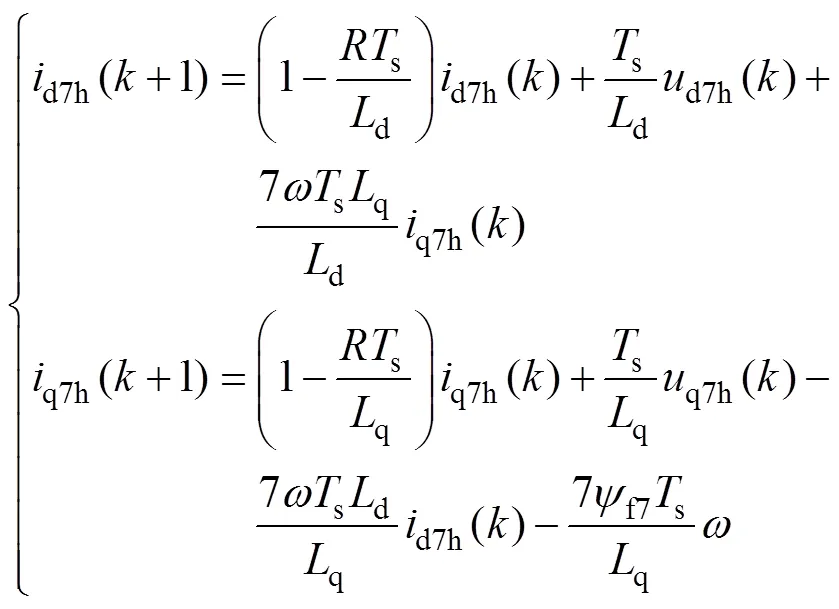
式中，d7h()q7h()分别为7次d、q轴谐波电流在第个采样周期内的值；d7h(+1)、q7h(+1)分别为7次d、q轴谐波电流在第+1个采样周期内的值；d7h()q7h()分别为7次d、q轴谐波电压在第个采样周期内的值。

上述所提的谐波电流提取方法及补偿电压计算方法均适用于其他阶次谐波电流，基于无差拍电流预测控制的谐波电压补偿法的整体控制框图如图9所示。图中，dq_ref为电机d、q轴电流的给定值；dq_i为补偿电压值；dq_ref为d、q轴电压的给定值。

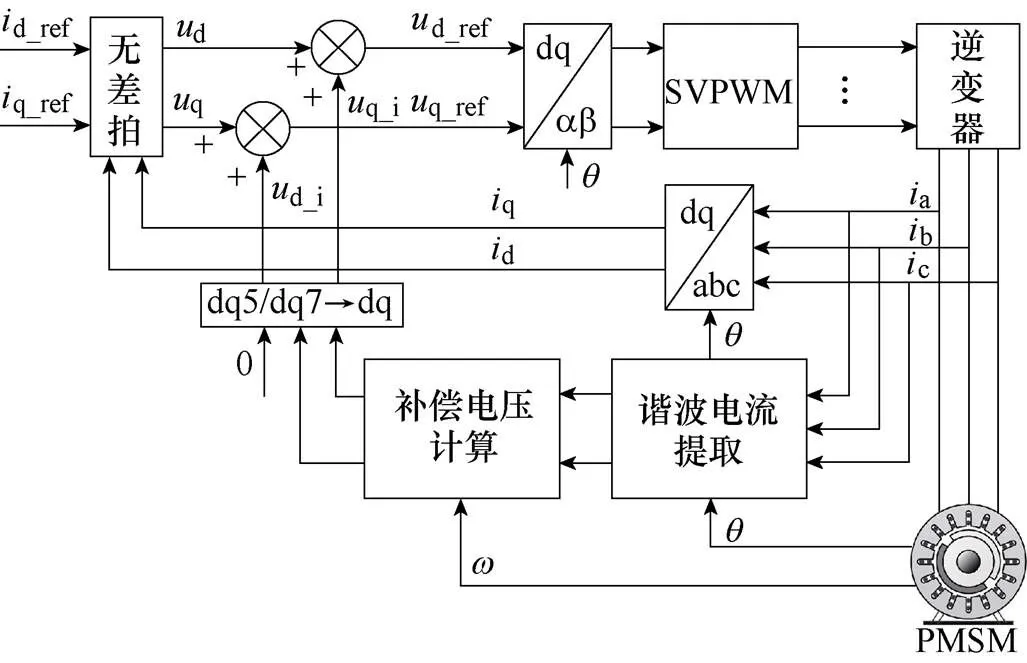
图9 基于无差拍电流预测控制的谐波电压补偿策略

3 仿真及实验结果

3.1 谐波电流提取方法仿真验证

为验证谐波电流提取方法的有效性，搭建了Matlab/Simulink模型并进行仿真研究。选用内置式永磁同步电机，其参数见表2。CDS中所用参数按第2节所述步骤选定，n=10Hz，p=1，i=0.1。

Matlab/Simulink仿真软件中自带的永磁同步电机模型是一个理想元件，其反电动势波形为正弦波，不含有由气隙磁场畸变引起的谐波电流。因此本文首先在Matlab/Simulink环境下建立了反电动势波形畸变的永磁同步电机本体模型，用于验证谐波电流抑制策略的可行性。电机本体模型的反电动势根据预先测得的实验电机畸变反电动势来设计，其波形如图10所示。

表2 IPMSM参数

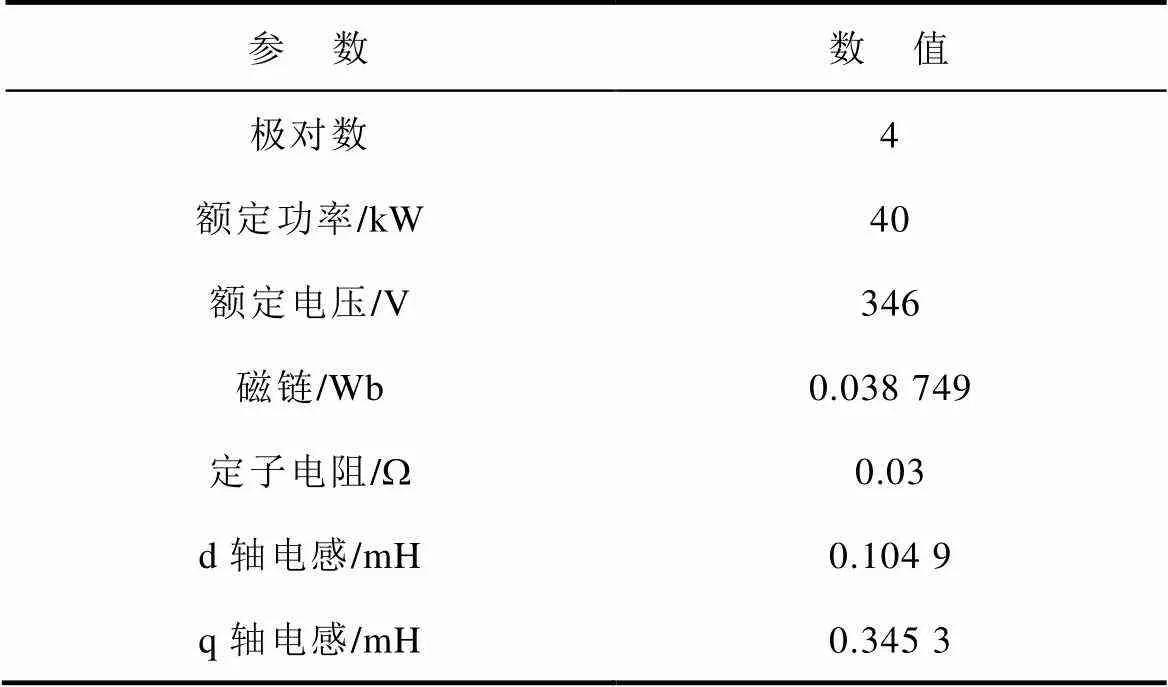
Tab.2 The parameters of IPMSM

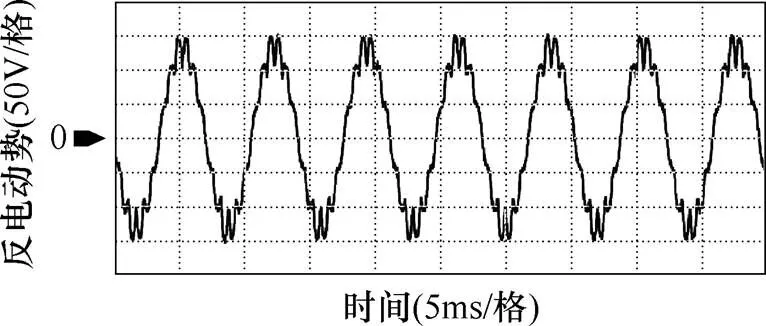
图10 实验电机反电动势波形

对畸变的反电动势波形进行傅里叶频谱分析，得到反电动势的谐波参数。以a相为例，反电动势谐波的幅值及初始相位见表3。

表3 实验电机各次谐波反电动势谐波幅值与相位

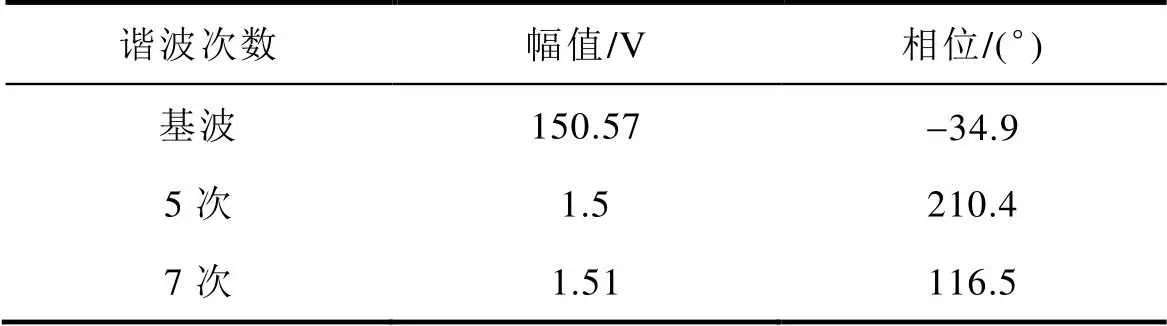
Tab.3 The harmonic amplitude and phase of each harmonic back EMF of experimental motor

仿真中设定的控制频率与逆变器开关频率均为10kHz。当电机转速为600r/min，负载转矩为40N·m时，以5次谐波电流为例，对比采用CDS提取出的谐波电流幅值与傅里叶分析得到的5次谐波电流幅值，对比结果如图11所示。图11a为变换到5次同步旋转坐标系下的定子电流波形，图11b为经CDS提取出来的5次谐波电流波形，图11c为对5次同步旋转坐标系下的定子电流进行快速傅里叶变换（Fast Fourier Transform, FFT）分析的结果。由图11可知，转速为600r/min，负载转矩为40N·m时提取出的5次d、q轴谐波电流幅值分别为2.6A和2A。由5次同步旋转坐标系下的定子电流的FFT分析结果可知，5次d、q轴谐波分量幅值为2.6A和2.03A，由以上对比可知，提取出的谐波电流幅值与FFT分析的结果一致。

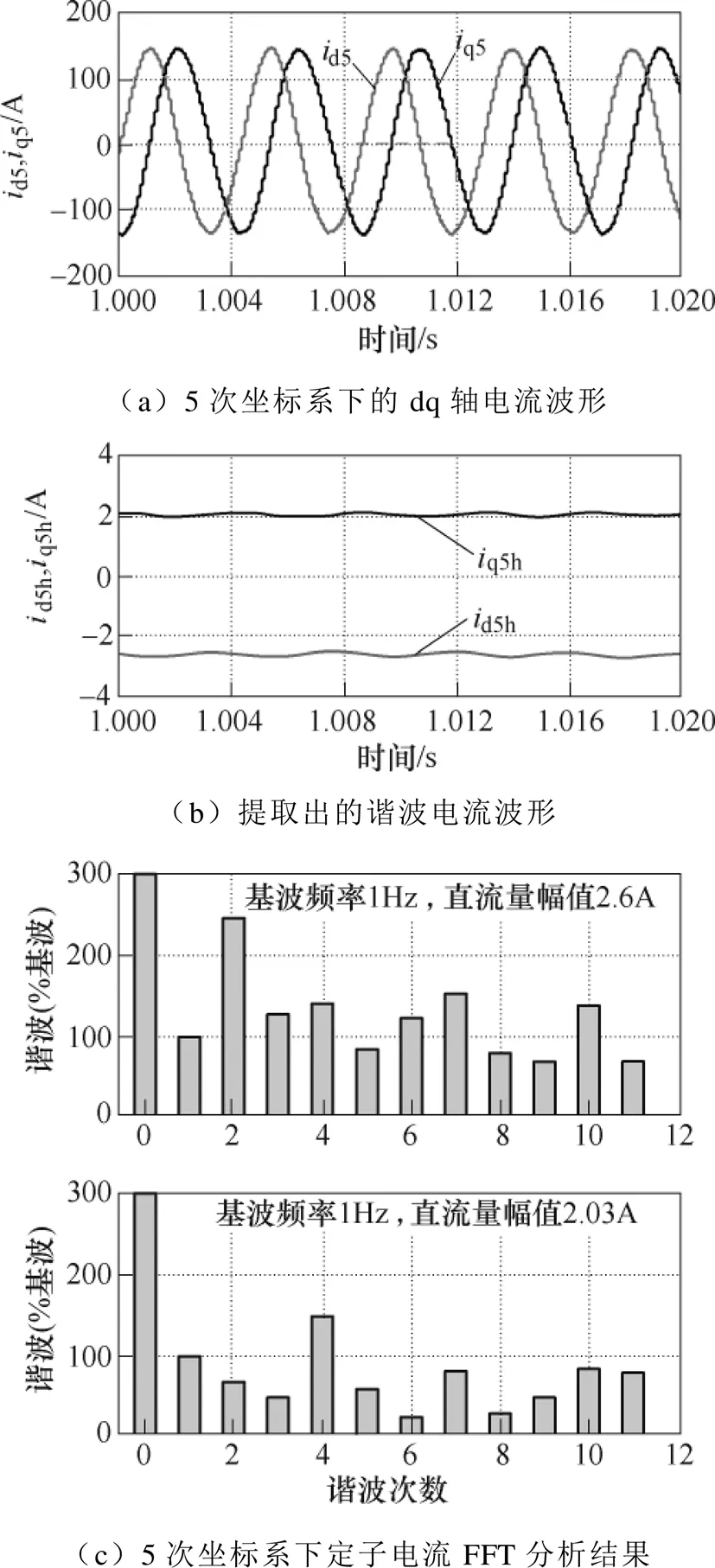
图11 谐波电流提取结果

3.2 电流谐波抑制方法实验验证

为了验证所提方法对电流谐波的抑制效果，选用电机参数与仿真参数相同的内置式永磁同步电机进行实验验证，搭建电机控制系统实验平台，如图12所示。其中控制单元由数字信号处理器（Digital Signal Processor, DSP）和现场可编程门阵列（Field Programmable Gate Array, FPGA）芯片组成。控制系统的采样频率与载波频率均为10kHz，负载由测功机提供。

图13为电机转速600r/min、负载转矩40N·m时，谐波电流抑制前后的电流波形及FFT分析结果。

根据图13将谐波电流抑制前后的实验结果绘制成表格，见表4。

图12 实验平台

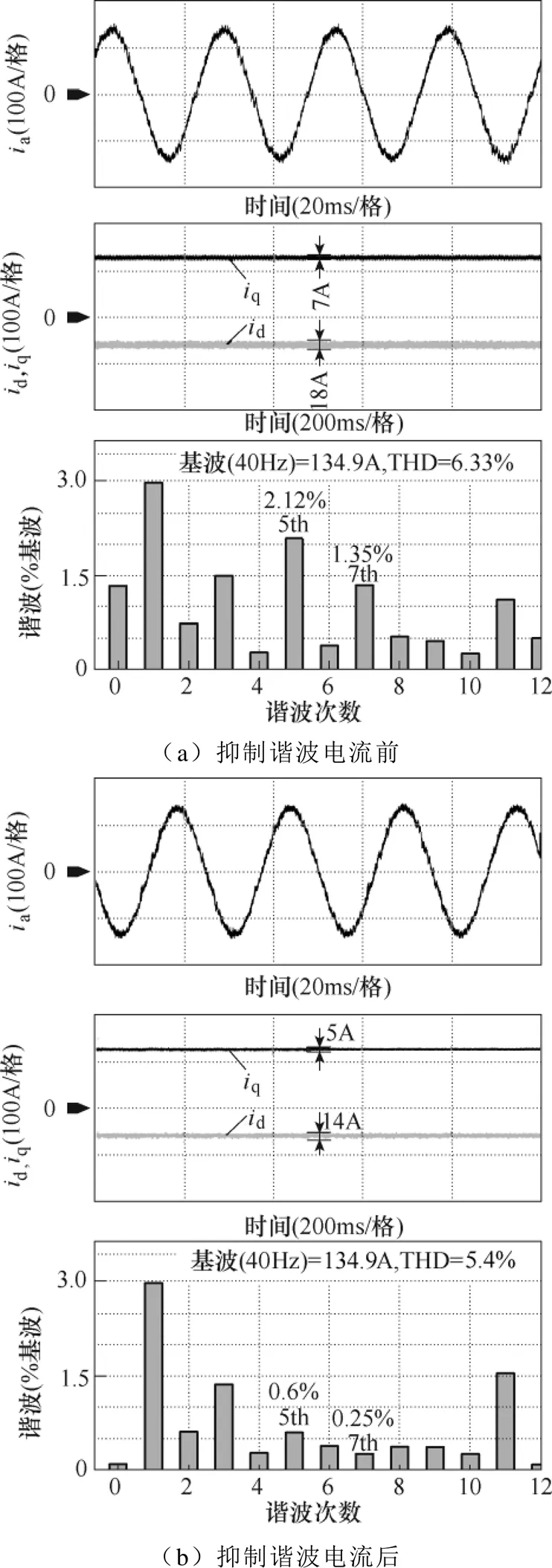
图13 600r/min、40N·m时的谐波电流抑制结果

表4 实验结果对比

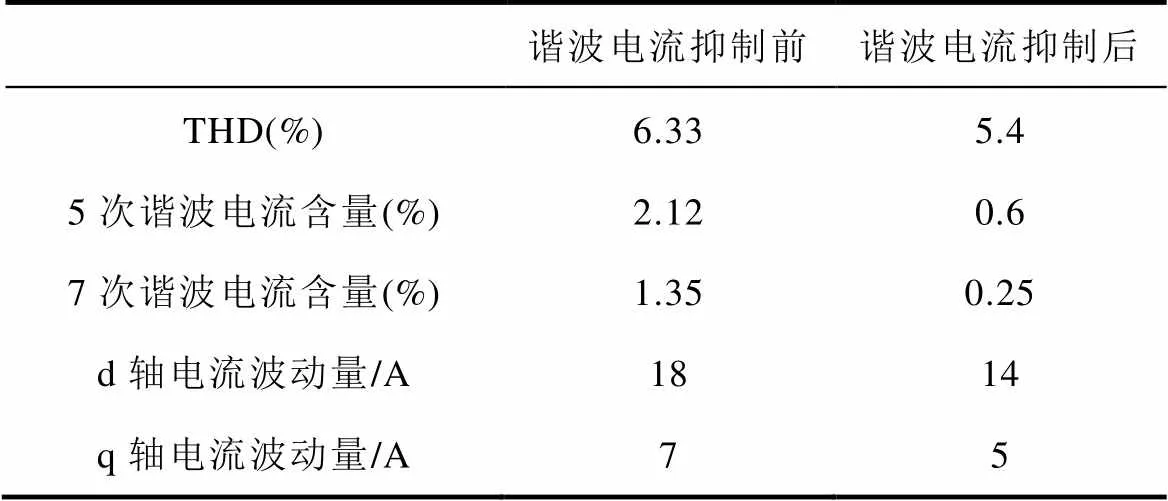
Tab.4 Comparison of experimental results

由表4可知，加入谐波电流抑制算法后，电机定子电流中5、7次谐波含量均有所下降，d、q轴电流波动量均有所减小，可知本文提出的谐波电流抑制算法能有效抑制电机低速时相电流中的5、7次谐波。

图14为电机转速1 800r/min、负载转矩40N·m时，谐波电流抑制前后的电流波形及FFT分析结果。

根据图14将谐波电流抑制前后的实验结果绘制成表格，见表5。

由表5可知，加入谐波电流抑制算法后，电机定子电流中5、7次谐波含量均有所下降，d、q轴电流波动量均有所减小，可知本文提出的谐波电流抑制算法能有效抑制电机转速较高时相电流中的5、7次谐波。

由上述实验结果可知，加入谐波电流抑制算法后，电机定子电流中5、7次谐波含量可减少60%～80%，d、q轴电流波动量明显减小，证明所提算法是有效的。

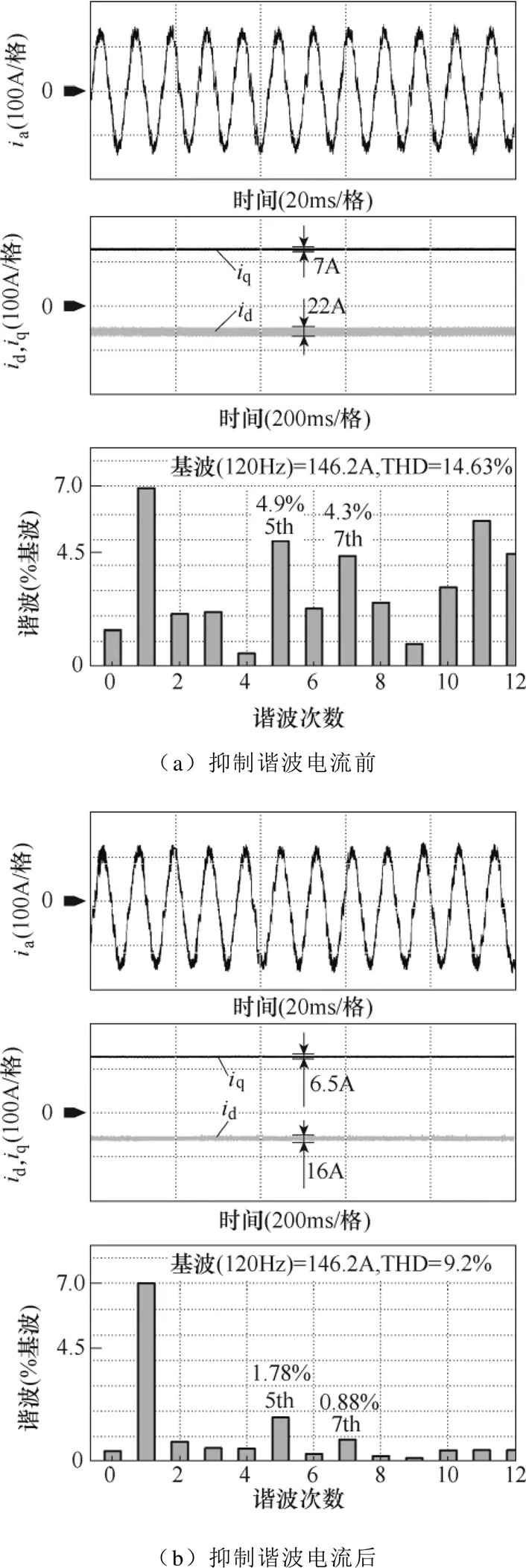
图14 1 800r/min、40N·m时的谐波电流抑制结果

表5 实验结果对比

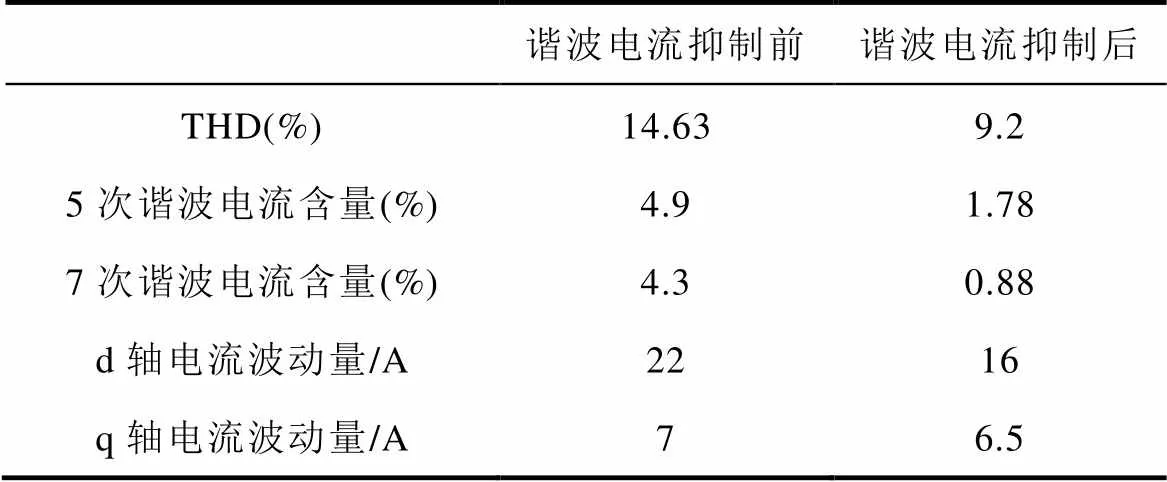
Tab.5 Comparison of experimental results

根据采样定理和数字信号处理器的工作性能可知，能够抑制5、7次谐波电流的最大转速与逆变器的开关频率有关[19]，其关系为

式中，sw为逆变器开关频率，因此，本文中最大有效频率max=167Hz，对应的最大转速为2 500r/min。

图15为负载转矩40N·m时，不同转速下对应的未加入谐波抑制算法和加入谐波抑制算法后5、7谐波电流含量的对比。

由图15可知，电机转速在2 100r/min以下时，加入谐波电流抑制算法后，5、7次谐波电流均能减小到2%以下，谐波电流抑制效果良好。而当电机转速超过2 100r/min后谐波电流抑制效果会逐渐减弱，从而验证了上述结论。

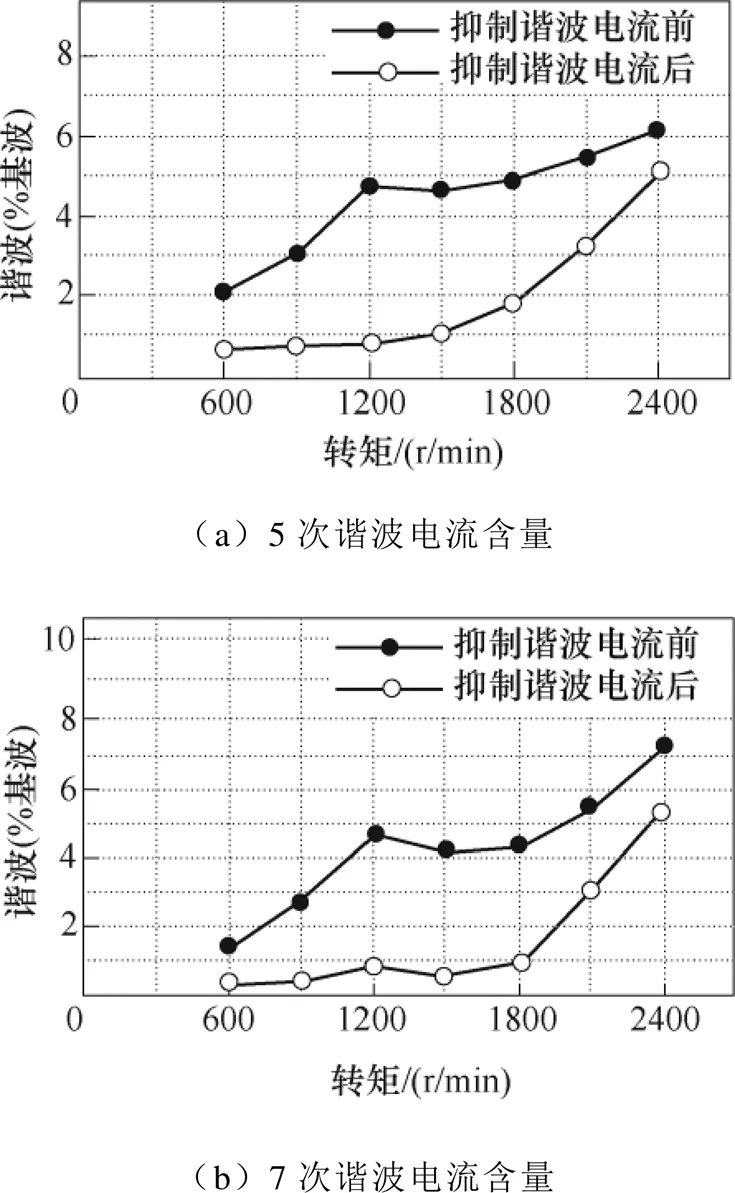
图15 转矩为40N·m时不同转速下的谐波含量对比

图16为电机转速1 800r/min时，不同转矩下对应的加入谐波抑制算法前后5、7次电流谐波含量的对比及结果。

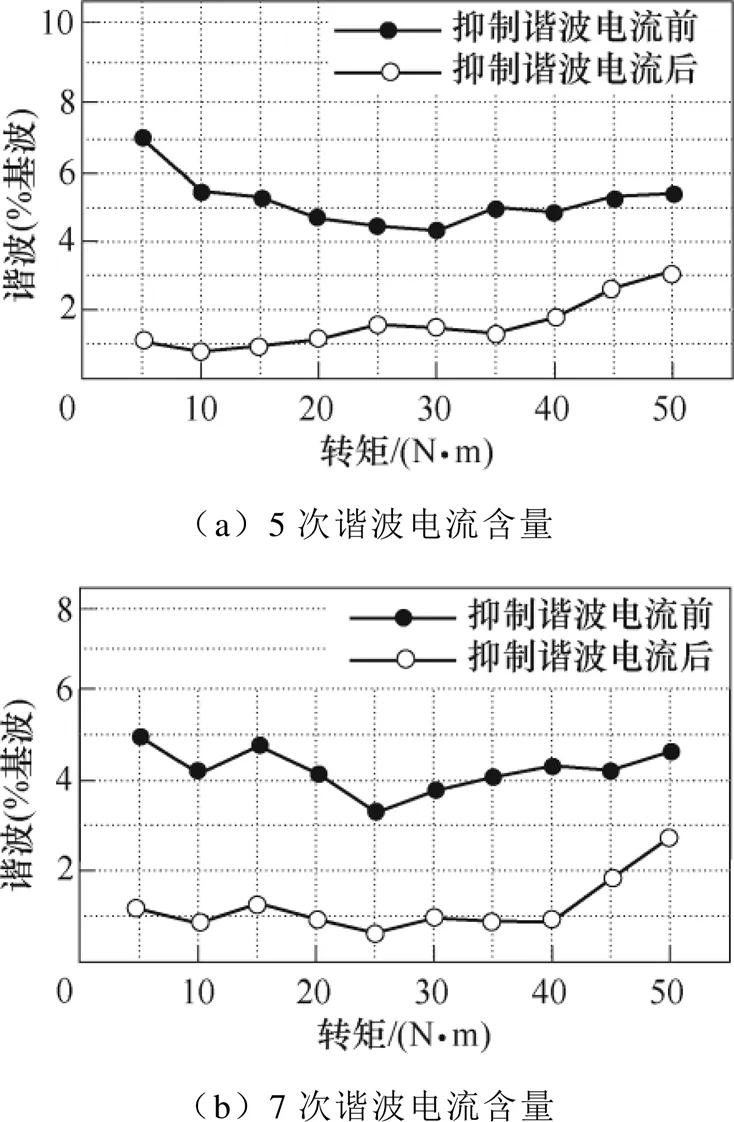
图16 转速为1 800r/min时不同转矩下的谐波含量对比

由图16可知，当负载转矩较小时，加入谐波电流抑制算法后，5、7次谐波电流均能减小到2%以下，谐波电流抑制效果良好。而当负载转矩超过35N·m后，随着负载增加，谐波抑制效果逐渐减弱。这是由于随着负载转矩增加，电机定子电流幅值变大，坐标变换后的定子电流中的交流分量幅值远大于直流分量，此时谐波电流的提取精度会降低，减弱了谐波抑制的效果。

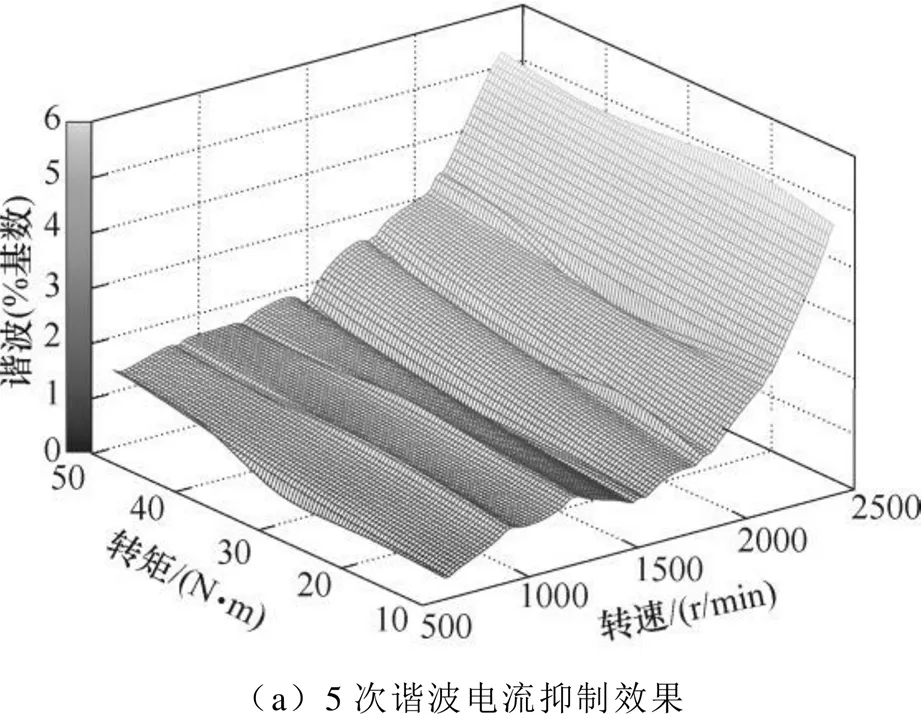
将加入谐波电流抑制算法后5、7次谐波电流随转矩和转速的变化趋势绘制三维曲面图，如图17所示。当电机运行速度接近2 500r/min或负载较大时谐波抑制效果会逐渐减弱，与上述分析结果相吻合。

4 结论

本文结合多同步旋转坐标系理论提出了一种谐波电流的抑制方法。首先，给出了含有谐波的永磁同步电机数学模型，并采用多同步旋转坐标系与LPF提取谐波电流；然后，在传统无差拍电流预测控制的基础上，增加抑制5、7次谐波电流的模块。与传统的控制算法相比，该算法不需要用到多个PI控制器，避免了由控制器延时所引起的电压误差，影响谐波电流补偿效果的问题，并且减小了参数整定的难度，易于实现。仿真与实验结果表明，该算法可以有效地抑制定子电流中的5、7次谐波电流，提高电流的正弦度，达到提升电机系统运行性能的目的。

[1] 姜燕, 李博文, 吴轩, 等. 基于比例谐振滤波的改进永磁同步电机转子位置观测器[J]. 电工技术学报, 2020, 35(17): 3619-3630.

Jiang Yan, Li Bowen, Wu Xuan, et al. An improved rotor position observer for permanent magnet syn- chronous motors based on proportional resonant filtering[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3619-3630.

[2] 李雪, 迟颂, 刘聪, 等. 基于虚拟电阻的永磁同步电机单电流调节器弱磁控制[J]. 电工技术学报, 2020, 35(5): 1046-1054.

Li Xue, Chi Song, Liu Cong, et al. Flux-weakening control with single current regulator of permanent magnet synchronous motor based on virtual resistor[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1046-1054.

[3] 李晓华, 赵容健, 田晓彤, 等. 逆变器供电对电动汽车内置式永磁同步电机振动噪声特性影响研究[J]. 电工技术学报, 2020, 35(21): 4455-4464.

Li Xiaohua, Zhao Rongjian, Tian Xiaotong, et al. Study on vibration and noise characteristics of interior permanent magnet synchronous machine for electric vehicles by inverter[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4455-4464.

[4] 尧磊, 秦雪飞, 蔡顺, 等. 内置式永磁电机转子硅钢片叠装错位对气隙磁场的影响[J]. 电工技术学报, 2021, 36(5): 1096-1100.

Yao Lei, Qin Xuefei, Cai Shun, et al. Influence of rotor lamination stacking misalignment on airgap field in interior permanent magnet motors[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(5): 1096-1100.

[5] Li Yu, Zhang Zhenbin, Li Kejun, et al. Predictive current control for voltage source inverters con- sidering dead-time effect[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(1): 35-42.

[6] Jezernik K, Horvat R, Čurkovič M. A switching control strategy for the reduction of torque ripple for PMSM[J]. IEEE Transactions on Industrial Infor- matics, 2013, 9(3): 1272-1279.

[7] Liu Chengcheng, Wang Kelin, Wang Shaopeng, et al. Torque ripple reduction of synchronous reluctance machine by using asymmetrical barriers and hybrid magnetic core[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(1): 13-20.

[8] Zhang Minjie, Ali N, Gao Qiang. Winding inductance and performance prediction of a switched reluctance motor with an exterior-rotor considering the magnetic saturation[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(3): 212-223.

[9] 罗玉涛, 卢若皓. 基于结构参数分级优化的电机电磁噪声抑制[J]. 电工技术学报, 2021, 36(14): 2957- 2970.

Luo Yutao, Lu Ruohao. Hierarchical optimization of structural parameters for motor electromagnetic noise suppression[J]. Transactions of China Electrotech- nical Society, 2021, 36(14): 2957-2970.

[10] 张海洋, 许海平, 方程, 等. 基于比例积分-准谐振控制器的直驱式永磁同步电机转矩脉动抑制方法[J]. 电工技术学报, 2017, 32(19): 41-51.

Zhang Haiyang, Xu Haiping, Fang Cheng, et al. Torque ripple suppression method of direct-drive permanent magnet synchronous motor based on proportional-integral and quasi resonant controller[J]. Transactions of China Electrotechnical Society, 2017, 32(19): 41-51.

[11] Li Dongsheng, Iwaji Y, Notohara Y, et al. Harmonic current cancellation method for PMSM drive system using resonant controllers[C]//2018 International Power Electronics Conference (IPEC-Niigata 2018- ECCE Asia), Niigata, Japan, 2018: 1301-1307.

[12] Kim H, Han Yongsu, Lee K, et al. A sinusoidal current control strategy based on harmonic voltage injection for harmonic loss reduction of PMSMs with non-sinusoidal back-EMF[J]. IEEE Transactions on Industry Applications, 2020, 56(6): 7032-7043.

[13] 麦志勤, 肖飞, 刘计龙, 等. 基于准比例谐振级联PI的双三相永磁同步电机谐波电流抑制策略[J]. 电工技术学报, 2018, 33(24): 5751-5759.

Mai Zhiqin, Xiao Fei, Liu Jilong, et al. Harmonic current suppression strategy of dual three-phase permanent magnet synchronous motor based on quasi proportional resonant cascading PI[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5751- 5759.

[14] 李毅拓, 陆海峰, 瞿文龙, 等. 基于谐振调节器的永磁同步电机电流谐波抑制方法[J]. 中国电机工程学报, 2014, 34(3): 423-430.

Li Yituo, Lu Haifeng, Qu Wenlong, et al. A per- manent magnet synchronous motor current suppression method based on resonant controllers[J]. Proceedings of the CSEE, 2014, 34(3): 423-430.

[15] 王贺超, 夏长亮, 阎彦, 等. 基于谐振控制的表贴式永磁同步电机弱磁区电流谐波抑制[J]. 电工技术学报, 2014, 29(9): 83-91.

Wang Hechao, Xia Changliang, Yan Yan, et al. Current harmonic suppression in the flux-weakening control of surface permanent magnet synchronous motors using resonant controllers[J]. Transactions of China Electrotechnical Society, 2014, 29(9): 83-91.

[16] Kim H, Bhattacharya S. A novel current control strategy based on harmonic voltage injection for power losses reduction of PMSMs with non- sinusoidal back-EMF[C]//2019 IEEE Industry Appli- cations Society Annual Meeting, Baltimore, MD, USA, 2019: 1-6.

[17] Chen Guodong, Zhu Miao, Cai Xu. Medium-voltage level dynamic voltage restorer compensation strategy by positive and negative sequence extractions in multiple reference frames[J]. IET Power Electronics, 2014, 7(7): 1747-1758.

[18] Wang Wusen, Liu Chunhua, Liu Senyi, et al. Current harmonic suppression for permanent-magnet syn- chronous motor based on Chebyshev filter and PI controller[J]. IEEE Transactions on Magnetics, 2021, 57(2): 1-6.

[19] Liu Gang, Chen Baodong, Wang Kun, et al. Selective current harmonic suppression for high-speed PMSM based on high-precision harmonic detection method[J]. IEEE Transactions on Industrial Informatics, 2019, 15(6): 3457-3468.

Harmonic Current Suppression Strategy for Permanent Magnet Synchronous Motor Based on Deadbeat Current Prediction Control

（National Local Joint Engineering Research Center of Electrical Machine System Design and Manufacturing Tiangong University Tianjin 300387 China）

In order to solve the problems of three-phase current distortion and high harmonic content during the operation of permanent magnet synchronous motors, this paper proposes a new harmonic current suppression method. Firstly, the expression of each harmonic current in the corresponding synchronous rotating coordinate system was analyzed. Then, a closed-loop harmonic current detection system was designed to extract the harmonic current. Finally, the deadbeat current prediction control strategy was used to suppress harmonic current by generating the compensation voltage. Simulation and experimental results show that this method can effectively suppress the harmonic current and improve the motor’s sinusoidal degree of the three-phase current. Moreover, the calculation is simple and easy to implement.

Permanent magnet synchronous motor, harmonic current, harmonic suppression, synchronous rotating coordinate transformation, deadbeat current prediction control

10.19595/j.cnki.1000-6753.tces.211856

TM351

国家自然科学基金（51977150）和天津市自然科学基金（19JCYBJC21800）资助项目。

2021-11-16

2021-12-16

谷 鑫 男，1980年生，教授，研究方向为高效能永磁电机系统及其控制方法。E-mail: guxin@tiangong.edu.cn

王志强 男，1984年生，副教授，研究方向为高速永磁电机系统设计与控制。E-mail: wangzhiqiang@tiangong.edu.cn（通信作者）

（编辑 崔文静）