机器人随机位置下动态无线供电阵列式发射模组优化设计

薛 明 杨庆新 章鹏程 郭建武 侯 虎

机器人随机位置下动态无线供电阵列式发射模组优化设计

薛 明1,2杨庆新1章鹏程1郭建武2侯 虎2

（1. 省部共建电工装备可靠性与智能化国家重点实验室（河北工业大学） 天津 300401 2. 天津工业大学天津市电气装备智能控制重点实验室 天津 300387）

为群智能行为研究和货物分拣场景中随机移动的多机器人实时补给电能，满足其不间断工作的需求是一个重要问题。该文提出一种基于有效耦合区域定量分析的阵列式电磁发射模组优化设计方法，可满足机器人在工作区域任意位置实时补给电能的需求。首先，分析了机器人运动过程中收发线圈存在的耦合情形以及相应的接收功率解析式。其次，提出了以满足机器人额定功率需求为基准，界定有效耦合区域的划分方法，并采用有限元分析方法定量表述了不同激励模式下的有效耦合区域，进而得到阵列式发射模组空间结构排布方法以及相应的线圈激励导通工作模态。最后，搭建了基于2×2阵列发射模组的小功率动态无线供电平台，验证了机器人随机位置动态无线获取电能补给的有效性。

阵列发射模组 动态无线供电 有效耦合区域 耦合机构 机器人

0 引言

无线电能传输（Wireless Power Transfer, WPT）技术作为一种新兴技术，其摆脱了传统电线的束缚，实现了电源与用电设备间的电气隔离，已成为各领域中研究的热点[1-5]。其中，在智能机器人领域，采用该技术可解决其在特殊场合以及极端条件下电能补给困难的问题，从而展现出极大的应用前景[6-9]。目前，科技工作者已开展了大量研究工作。

在机器人以无线充电方式补给电能方面，主要研究了机器人自主循迹到固定充电站静态无线充电和机器人在装有无线电能发射导轨的固定路径上动态无线取电两种方式。前者，机器人需要装载储能设备，同时应具有循迹到电源站的功能，并且对准确度要求较高[10-11]；后者，机器人可少量甚至无需安装储能设备，即可实现对电能的实时补给，延长了机器人不间断工作时间。因而，采用动态无线供电为机器人补给电能的方式研究较为广泛[12-15]。其研究方向主要包括以下几点：在动态耦合机构研究方面，文献[12]针对天然气管道巡检机器人动态无线供电系统，设计了由8个环形线圈组成的电能拾取机构，提高了系统抗偏移能力。在发射导轨激励模式方面，文献[13]针对电缆隧道巡检机器人动态无线供电过程中的导轨切换和错位问题，采用红外检测的方法，实现了发射线圈自动切换供电和待机之间的操作模式。在传输特性研究方面，文献[14]基于集中式能量接收和分散式能量接收的统一电路模型，设计了机器人动态无线供电系统，并得到分散式能量接收系统开关点处接收功率和效率指标更佳的结论。

对上述研究分析可见，静态充电对机器人充电桩位置导航定位和收发线圈位置对准两个方面提出了较高要求，增大了系统的控制难度，并且机器人需停止当前工作，工作效率降低。若采用分段式动态无线供电，虽然能较好地解决上述问题，但是负载侧接收功率波动性较大，并且机器人运动路径上偏移容忍度有限，工作范围较为固定。可见，目前无线电能传输技术的研究在机器人场景电能补给中存在一定的局限性，无法有效满足机器人在特定应用场景中，对持续不间断电能补给的需求。例如，在群智能行为的研究中，单体机器人间协同工作模拟自然界中群体动物智能行为，其移动位置往往不可预测[16-17]，并且持续工作时间长达数小时甚至更长时间。可见，该应用场景下机器人工作过程中移动位置具有很大的随机性，并且对持续不间断工作要求较高。显然，采用目前的静态充电以及固定路径下的动态无线供电将无法满足应用需求。

本文基于机器人工作过程中位置具有随机性的特点，采用有效耦合面积定量分析方法，优化设计了一种可满足机器人在任意位置下动态无线补给电能的阵列式电磁发射模组结构，针对该种结构，目前已有文献基于电子设备静态充电应用场景进行了研究，文献[18]提出了由4个立体形线圈组成的阵列结构，传输效力较低，不具有实用性。文献[19]研究了中继耦合的阵列线圈，由于线圈间的交叉耦合较大，容易出现频率分叉现象，造成传输效率快速跌落。文献[20-21]的研究从阵列线圈结构上改进了上述问题，分别提出了线圈重叠式以及平面型、立体性和可重构模块的阵列线圈结构优化设计方法，增大了能量传输覆盖范围，实现了较高的传输效率均匀度。以上对阵列线圈的研究均是基于负载静态充电场景，可实现多负载供电需求。然而，当该种结构应用于多动态负载场景中，由于发射线圈模组无法实现分区域灵活控制，负载工作过程中，发射侧电路需始终保持开启状态。可见，从耦合效率上考虑，显然不适用于移动机器人随机位置下动态无线供电场景。

文献[22-23]采用阵列模组分区域控制的方法，根据不同电子设备尺寸和位置信息激发对应区域内的线圈单元导通工作，有效减小了空间漏磁，其方法可为机器人动态无线供电提供指导，但由于其充电对象为静止负载，不涉及负载运动过程中处于不同耦合区域下线圈激励模式的切换问题，无法有效支撑机器人随机位置下动态无线补给电能场景的应用，因而，针对该问题，本文基于有效耦合区域的分析，定量划分不同激励模式所对应的耦合边界区域，为机器人动态工作中线圈激励模式切换临界点的选择提供参考依据。

首先，本文分析了机器人实际运动过程中电能收发端存在的耦合情形，并推导了每种情形下系统传输功率解析表达式。其次，以机器人额定功率为基准，对单发射线圈、双发射线圈及四发射线圈三种激励模态下的有效耦合区域进行分析以及定量表述。最后，搭建了基于2×2阵列线圈的小功率动态无线供电平台，验证了该设计的正确性与有效性。

1 动态无线供电磁耦合情形分析

在阵列式电磁发射模组空间结构排布设计中，为了在供电区域内最大限度减少单体发射线圈的使用数量，以达到减小铺设成本的目的，应在满足负载供电需求的前提下，使各单体发射线圈的相邻区域尽可能增大。然而在不增大系统输入功率的条件下，仅采用单体发射线圈切换的激励工作模式将无法呈现显著效果。因此，在阵列式发射模组中单体发射线圈相邻区域必将采用两个或多个线圈同时供电模式，以弥补单体发射线圈电能供给不足的缺陷。

因而，通过分析多机器人协同工作系统中单体机器人运动过程可知，机器人处于阵列式发射模组上方不同位置处，要实现稳定补给电能的目标，电磁收发线圈需采用单发射-单接收、双发射-单接收、四发射-单接收三种耦合模式，如图1所示为阵列式发射模组中收发线圈耦合情形示意图。接收线圈A和F所在区域处于单发射-单接收耦合机构偏移容忍度范围内，采用单发射激励即可满足机器人负载的供电要求，因而只需激发单发射线圈导通工作即可。接收线圈C和D处于两个发射线圈的中间区域，该区域内采用单发射线圈不足以满足负载的功率需求，必须采用双发射线圈同时激励的方法。同理，在接收线圈处于B和E情形中，即四发射线圈的中心区域内，该区域已超出单发射与双发射线圈所能供给的能量范围，必须采用4个发射线圈同时激励的方法。

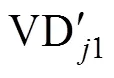
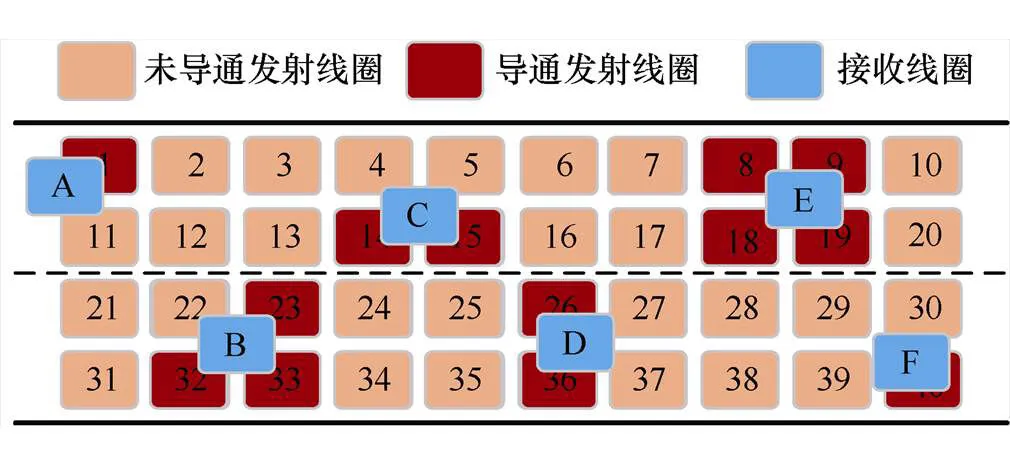
图1 收发线圈耦合情形示意图

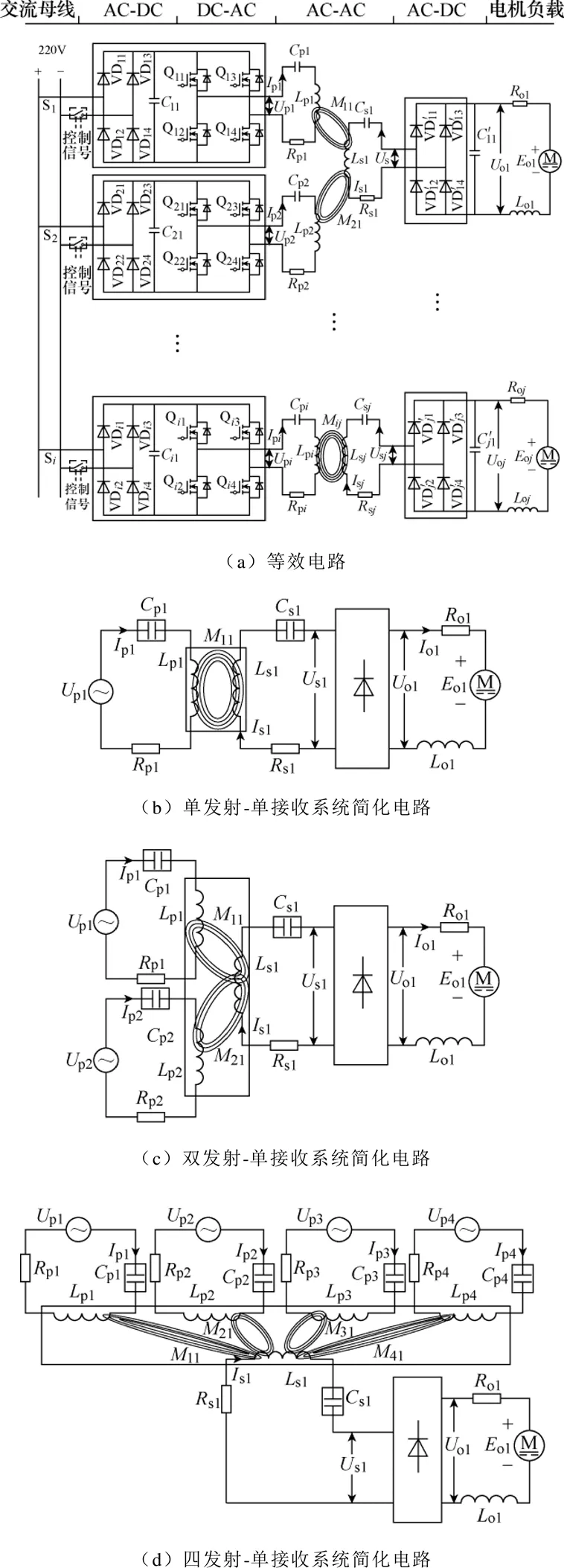
图2 系统等效电路模型

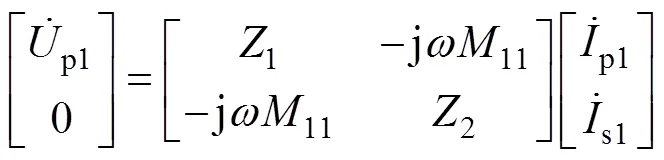
其中

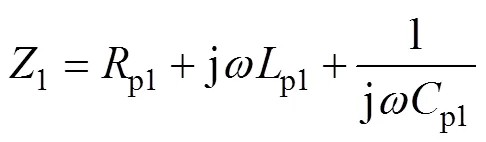
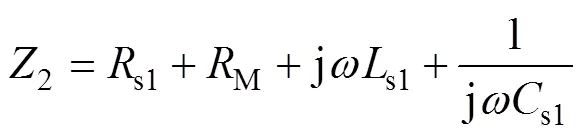
式中，1和2分别为发射侧和接收侧主回路的等效阻抗；M为接收侧LC谐振网络后端电路等效电阻。

在机器人额定工作过程中，对于直流电机负载，o1为恒值，电枢电感o1上电压降为零，则可得到电机两端电压o1和电磁转矩E分别为

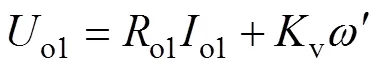
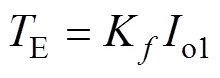
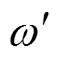
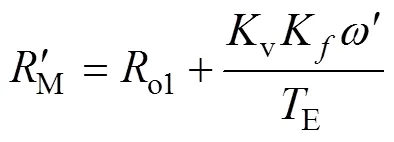
由于直流电机工作在额定值，电磁转矩和转速分别为额定值N和N，则接收侧LC谐振网络输出端口后侧电路的等效阻抗M可表示为

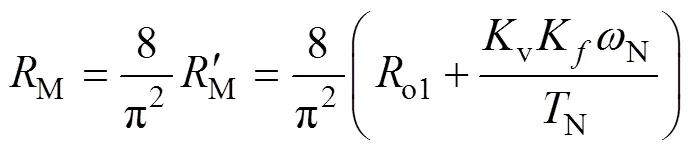
由式（7）知，电机负载以额定参数运行，其M为恒定值。此外，通过式（1）～式（3）可计算在谐振条件下，系统接收回路电流为

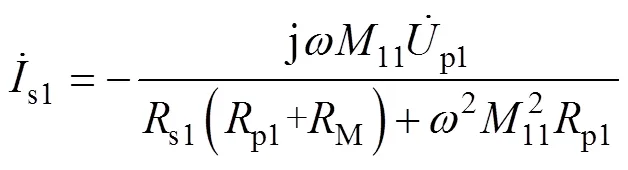
则接收侧LC谐振网络拾取功率表达式为

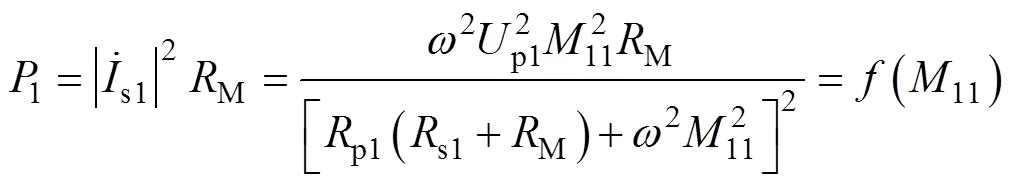
同理，在谐振条件下，可得到图2c双发射-单接收系统和图2d四发射-单接收系统接收回路电流和拾取功率表达式，其中激励源电压值相等，由于相邻发射线圈处于同一平面，并且实际排布中距离较大，因而计算中忽略相邻发射线圈间的互感，结果为

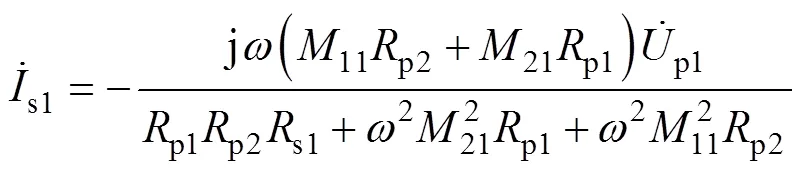
（11）

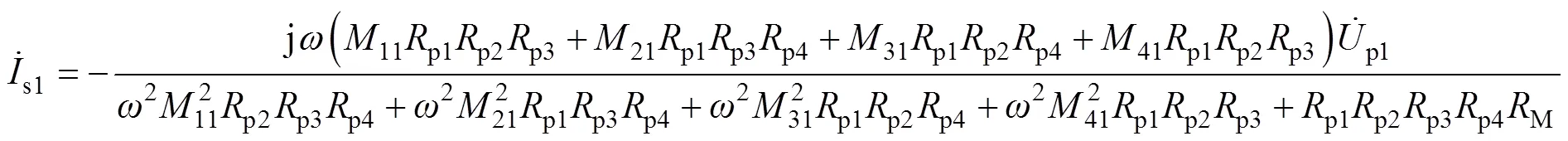
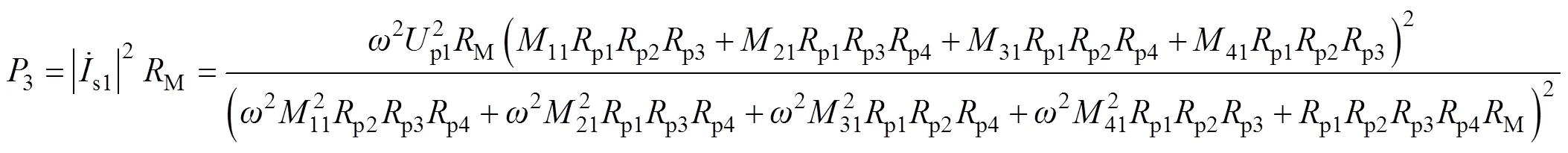
式中，2和3分别为双发射-单接收与四发射-单接收系统接收侧谐振网络拾取功率。

从式（9）、式（11）和式（13）可知，在单发射、双发射和四发射分别与单接收线圈耦合情形下，直流电机负载工作于额定状态，接收侧谐振网络拾取功率主要与输入电压、谐振网络后端等效电阻、角频率、线圈间互感以及器件等效内阻有关。当在特定应用场景中，无线供电系统功率等级以及系统参数限定，拾取功率呈现出的波动性主要受耦合机构互感参数影响，而实际工作过程中互感参数与阵列线圈的空间排布与负载位置直接相关。因而，为了使机器人负载在动态无线供电区域内任意位置处均能稳定可靠获取电能，必须对阵列式发射线圈空间排布结构进行深入分析。

2 不同耦合情形下有效耦合区域定量分析

2.1 有效耦合区域定义

发射线圈通入高频交流激励，在空间产生交变磁场，其磁通密度在空间内不同区域差异性较大，因而与接收线圈相交链的磁通量随接收线圈位置变化，并且在不同的传输距离内，当通过发射线圈与接收线圈中心点的轴线重合时，穿过接收线圈的磁通量较大，接收线圈两端产生的感应电动势具有最大值，当接收线圈延某一方向偏移中心轴线，则感应电动势非线性减小。可见，只要与接收线圈相交链的磁通量不为零，那么收发端就会发生耦合，并且接收线圈所在位置处形成的集合，均可作为电能收发端的磁耦合区域。

当接收线圈中心沿任意方向偏移，感应电动势减小到一定程度将无法达到负载电能补给参数要求，造成负载无法工作于额定状态，甚至停止工作。为了保证负载可靠稳定获取能量，有必要对收发端空间耦合区域进行定量划分。因而，本文提出以满足负载额定功率工作要求为基准，将发射线圈与接收线圈空间耦合区域划分为有效耦合区域和无效耦合区域，即电能发射端与接收端耦合距离一定，将收发端中心轴线重合时的位置设为起点，接收线圈中心点偏移该轴线，将能满足负载以额定功率工作的接收线圈所在位置建立集合，形成的区域作为有效耦合区域。当接收线圈中心点继续偏移中心轴线，则将无法满足负载额定功率要求，将该区域作为无效耦合区域。

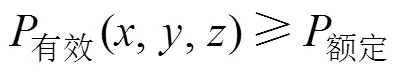
2.2 单发射激励有效耦合区域

单发射线圈是组成阵列式发射模组的最基本单元，其有效耦合区域直接影响阵列式结构线圈单元间的空间排布。本文以方形结构作为构成阵列式发射模组的基本单元结构，并采用有限元数值分析方法对有效耦合区域定量分析。

在单发射-单接收耦合机构仿真模型中，收发线圈参数一致，匝数为10匝、外直径为200mm、内径为120mm、线圈电感为41.26mH。此外，在与该模型耦合的外电路中，激励采用幅值s=100V、频率为85kHz、传输距离为100mm、接收线圈和发射线圈两侧均采用串联-串联（Series-Series, SS）补偿电路拓扑、调谐电容为84.98nF、负载采用10W电阻等效。

根据耦合区域的划分准则定量分析有效耦合区域中，使接收线圈在发射线圈上方100mm处的平面内自由移动并记录下各点的功率值。本文假定机器人额定功率为50W，并且以接收线圈中心点位置定量表示有效耦合区域。为了简化分析，基于系统对称性的特点，只研究耦合系统的1/4区域，其结果如图3所示。由结果可知，系统接收功率与接收线圈位置密切相关，并且当接收线圈位于所在平面不同位置时，在收发线圈几何中心点连线距离相同的点位，系统输出功率相等。

如图3b所示，在功率分布中绘制功率等于50W的等高线，可以发现，其是以原点为中心，半径为87.85mm的弧线。由此，对于额定功率为50W的额定负载，该系统中单发射线圈的有效耦合区域根据接收线圈中心点所在位置可定量表示为以发射线圈几何中心为原点，直径为175.7mm的圆形区域，如图4所示。因此，接收线圈的中心处于该区域范围内，即可实现机器人的稳定供电。考虑不同类型的机器人由于底盘高度不同，造成有效耦合区域的变化，本文进一步探究了系统有效耦合区域与传输距离的定量关系，从而使有效耦合区域的分析更具一般性，接收功率波动曲线如图5所示。由结果可知，随着传输距离的逐步增大，接收功率从大到小，负载正常工作额定功率50W（互感7.93mH）对应的轴偏移容忍距离逐渐减小，在传输距离达到150mm，即使系统收发线圈处于中心线径向重合的理想位置也无法满足负载正常工作。如图6所示为圆形有效耦合区域的半径与传输距离的关系，并呈现出负相关变化规律。

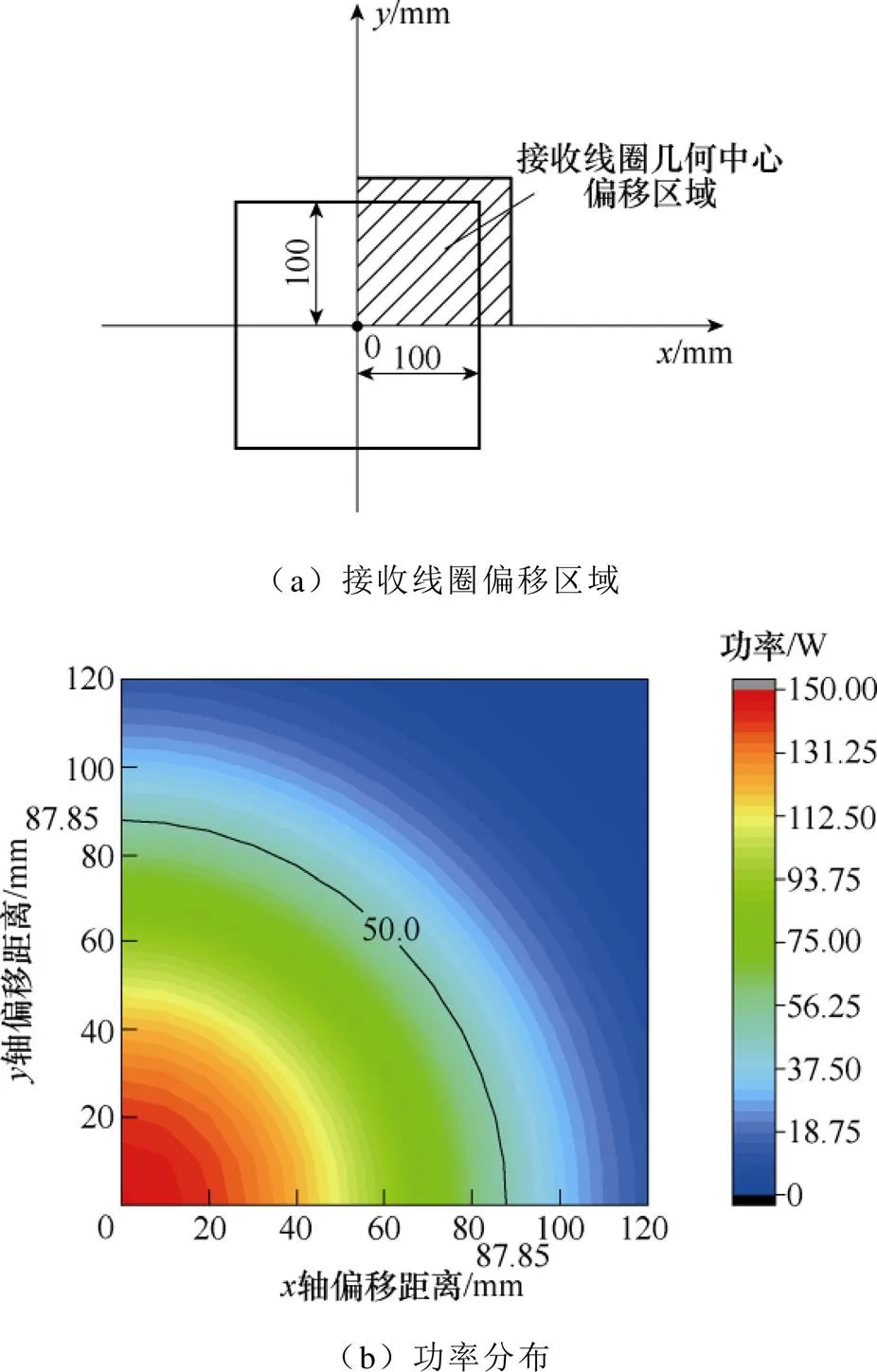
图3 单发射激励接收线圈偏移区域及功率分布

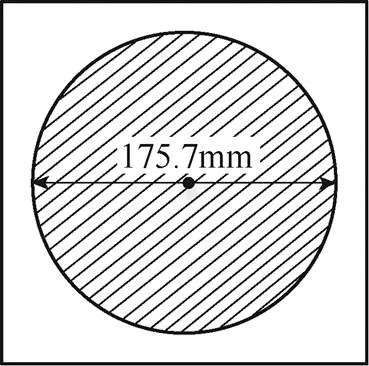
图4 单发射激励有效耦合区域定量表示

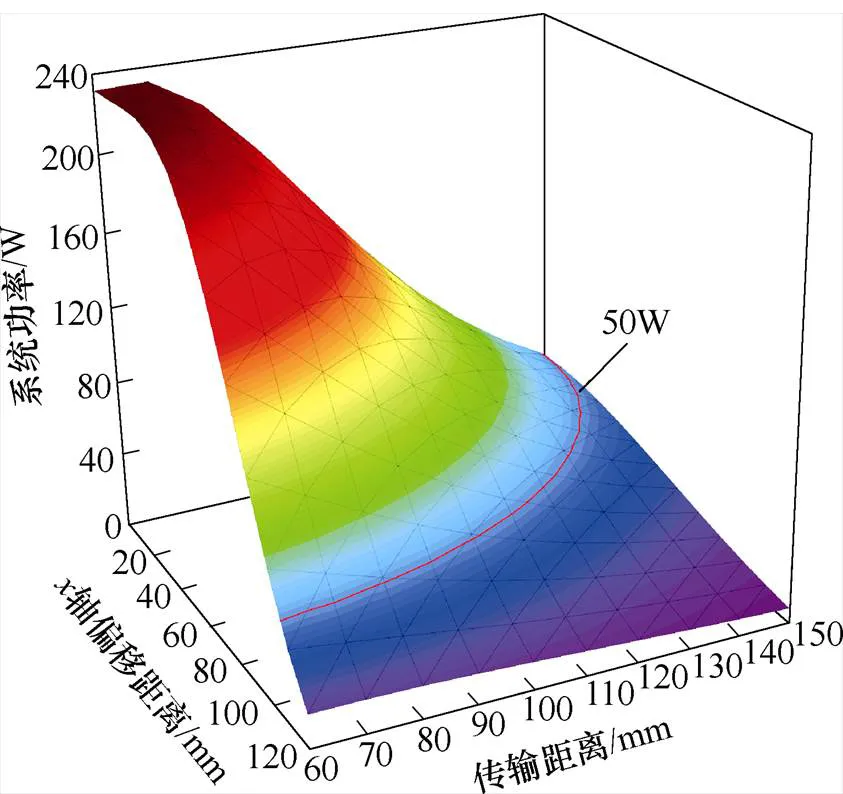
图5 接收功率波动曲线

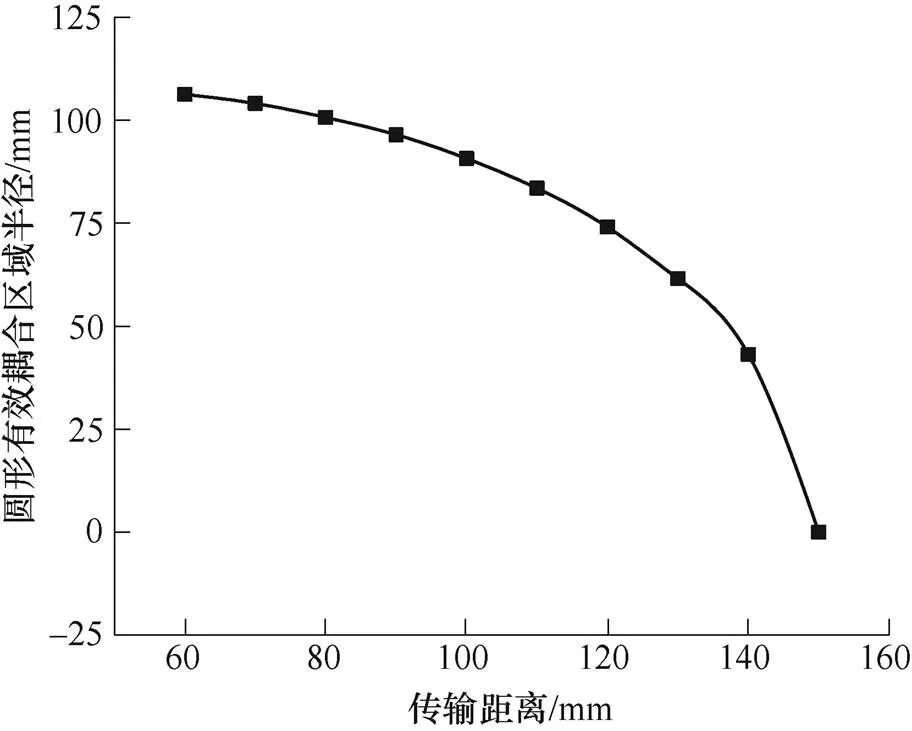
图6 有效耦合区域半径变化曲线

2.3 双发射激励有效耦合区域

当机器人移动位置处于单发射激励的有效耦合区域外部，机器人将无法获得足够的能量，此时需要开启邻近发射线圈单元同时为机器人供给能量，从而构成双发射激励系统。因此，需要研究接收线圈在双发射线圈上方任意位置下的功率分布，确定双发射单元有效耦合区域。从双发射激励线圈排布结构可知，相邻发射线圈之间的排布间隙是双发射激励有效耦合区域判定的重要参数。双发射激励系统接收线圈偏移区域和功率分布如图7所示。在分析过程中，保持两个发射线圈激励相位一致，并且利用对称性将接收线圈轴偏移距离初始位置设置为-120mm，并以步长为20mm偏移增加至340mm，轴偏移距离初始设置为0，以步长为10mm偏移距离增加至120mm，如图7a所示。

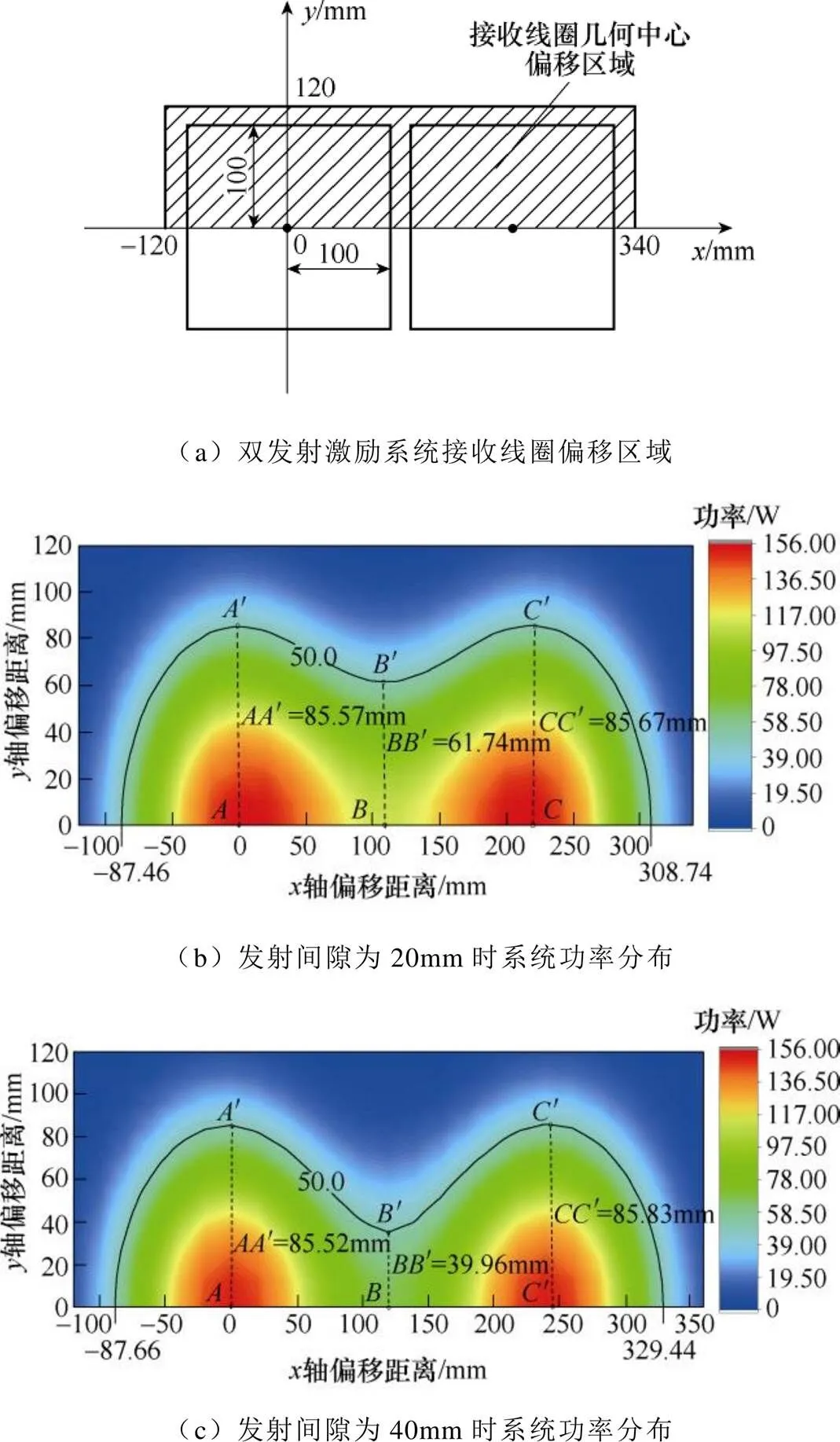
图7 双发射激励系统接收线圈偏移区域和功率分布

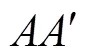
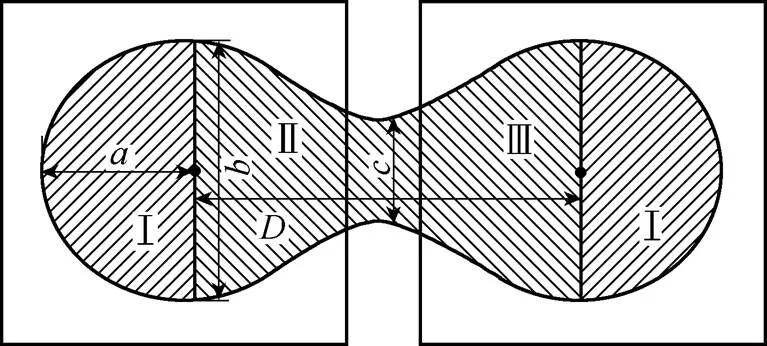
图8 双发射激励系统有效耦合区域

由以上分析可知，在双发射线圈同时激励工作模式下，相邻发射线圈的间隙对有效耦合区域的影响主要可通过Ⅱ类区域中的、的值的变化表征，其中为两发射线圈几何中心点的距离，即线圈间隙和线圈外径之和，而与线圈间隙的关系较为复杂，需针对发射线圈间隙对双发射线圈系统有效耦合区域的影响规律以及定量关系进一步分析。

图9为不同间隙下接收线圈在双发射激励间隙中线运动时的功率分布。由结果可知，双发射线圈的间隙减小，接收功率呈增大趋势，并且从50W接收功率等高线可知，随着发射线圈的间隙增大，双发射线圈有效耦合区域中Ⅱ类区域中的值逐渐减小，且当间隙为50mm时，其为零。

图9 不同间隙下双发射激励中线处的功率分布

综上所述，双发射激励有效耦合区域为Ⅰ、Ⅱ类区域的组合，其中Ⅰ类区域基本不受发射线圈间隙影响，可由、的值表征，当负载功率为50W时，=87mm，=170mm；Ⅱ类区域为“沙漏”状区域受发射线圈间隙影响较大，可由、、的值表征。其中，与间隙有关，且值与发射线圈间隙定量关系如图10所示。

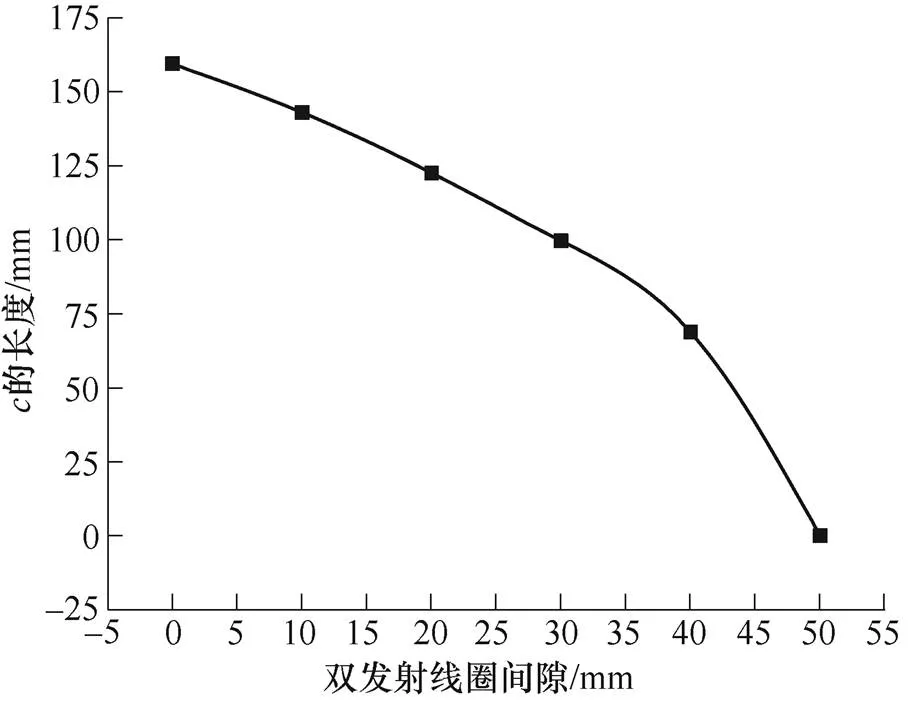
图10 发射间隙改变情下Ⅱ类区域中参数变化曲线

2.4 四发射激励有效耦合区域

由机器人动态供电过程分析可知，当接收线圈处于四发射线圈中间区域时，仍然存在不能满足负载额定功率需求的盲区。可见，仅单发射与双发射激励两种模式切换供电仍不能保证机器人在阵列发射线圈上方任意位置均能正常工作的需求。因而，需对四发射线圈同时供电情形下的有效耦合区域进行研究。四发射激励接收线圈偏移区域、功率分布及有效耦合区域如图11所示。在分析过程中，接收线圈几何中心的运动区域轴和轴方向均为[-110mm, 110mm]，步长为20mm，相邻发射线圈间隙设置为20mm不变，其示意图如11a所示。

图11b为接收线圈在四发射线圈上方1/4区域运动时的功率分布，绘制50W接收功率的等高线，再根据对称性可知，四发射激励有效耦合区域分布如图11c所示。由结果可知，在四发射激励有效耦合区域内，功率最大值在单发射线圈中心处，而在中间区域功率较低。为了使机器人在四线圈发射单元的中心部分也能满足功率需求，需进一步对发射线圈间隙改变时，接收线圈处于四线圈发射单元的中心位置时的功率进行研究分析。

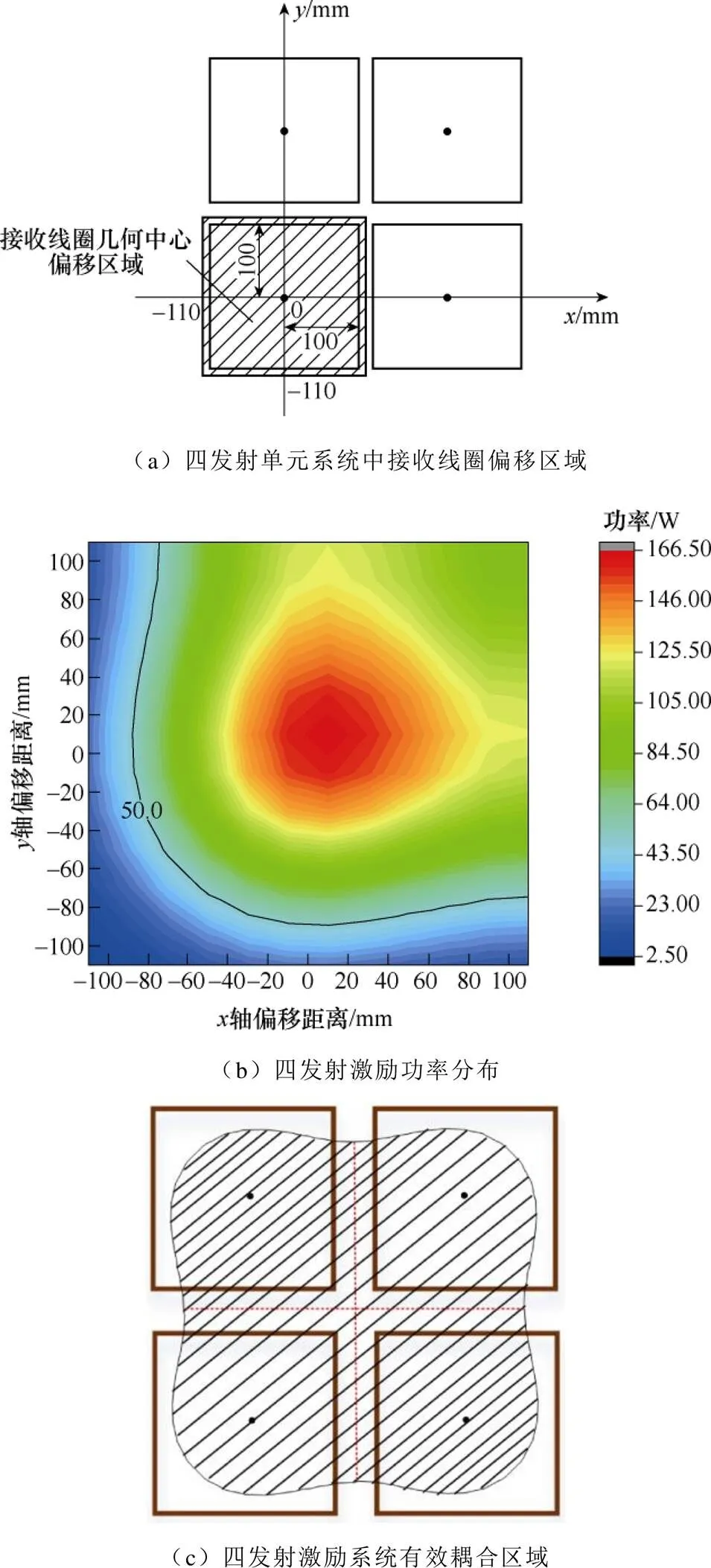
图11 四发射激励接收线圈偏移区域、功率分布及有效耦合区域

图12为当相邻发射线圈间隙改变时，接收线圈位于四发射线圈中心位置处的功率变化曲线。从图中可知，在线圈间隙的增大过程中，中心点处的功率逐步下降，且当间隙为35.66mm时，系统功率下降为50W。因此，为保证机器人在四发射线圈中心区域能够正常工作，相邻发射线圈间隙应设置在0～35.66mm区间内。

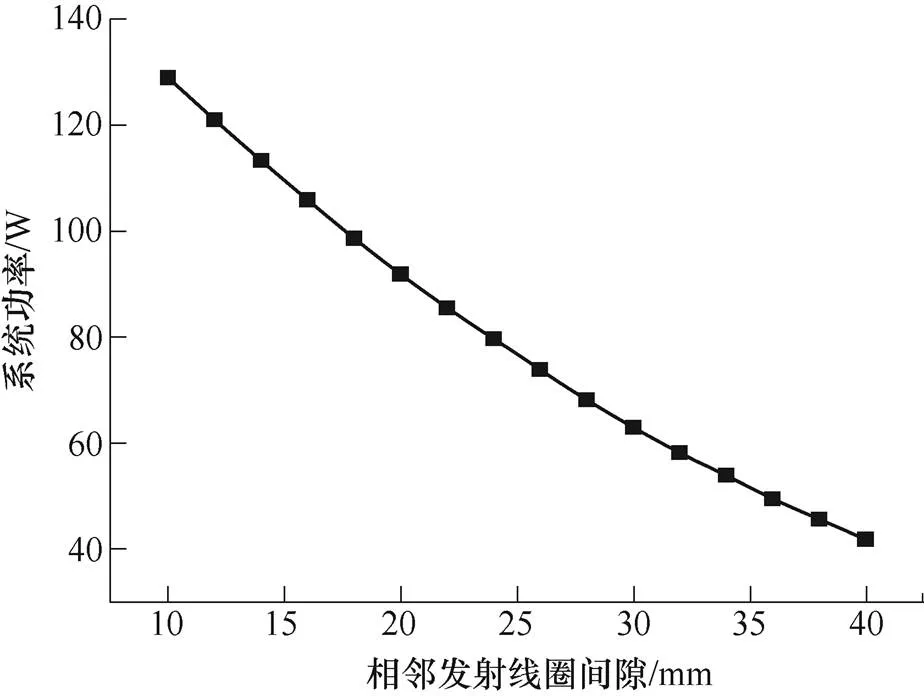
图12 间隙改变情形下四线圈中心点的功率变化

3 阵列式发射模组结构设计

3.1 阵列式发射结构设计准则

为了实现机器人在工作区域任意位置处均能可靠获取电能补给的目标，本文提出将多个单发射线圈按照一定规则铺设于机器人工作区域，组成阵列式电能发射机构，并且从双发射线圈和四发射线圈的有效耦合区域定量分析结果可知，相邻发射线圈的间隙是决定其空间排布的重要参数。双发射线圈可为相邻线圈间隙的部分区域正常供电但十分有限，因而不能以此确定阵列式发射模组相邻线圈间隙。四发射线圈能够使机器人处于线圈间隙的全部区域都能正常工作，并且满足额定功率值的中心区域是决定阵列线圈的排布间隙取值的关键。

此外，在实际工况下由于需要铺设大量的电能发射线圈单元满足机器人任意位置动态无线供电需求，其线圈的排布间隙与线圈铺设数量直接相关，因此在阵列线圈间的排布间隙取值选择中，还应考虑材料成本，尽量减少发射线圈的铺设。

综上所述，机器人动态无线供电系统的阵列式发射模组设计应遵循两点原则：第一，四线圈中心区域系统功率不小于负载额定功率；第二，在满足负载额定功率需求基础上，实现发射线圈排布间隙最大化。

3.2 阵列式发射模组结构设计流程

依据阵列式发射模组设计的遵循原则，阵列式发射模组结构设计流程如图13所示。首先，根据特定机器人充电参数以及本体结构特点，确定机器人的额定功率以及系统耦合线圈的尺寸；其次，通过有限元数值分析，得到单发射线圈的有效耦合区域以及相邻发射线圈间隙不同时的双发射线圈、四发射线圈的有效耦合区域边界值；再次，按四线圈中心区域满足额定功率限值以及整体覆盖面积最大的原则确定相邻线圈间隙，并以定量分析结果为依据铺设阵列线圈；最后，依据分析得到的系统三种激励模态下的有效耦合边界划分阵列线圈的切换区域。

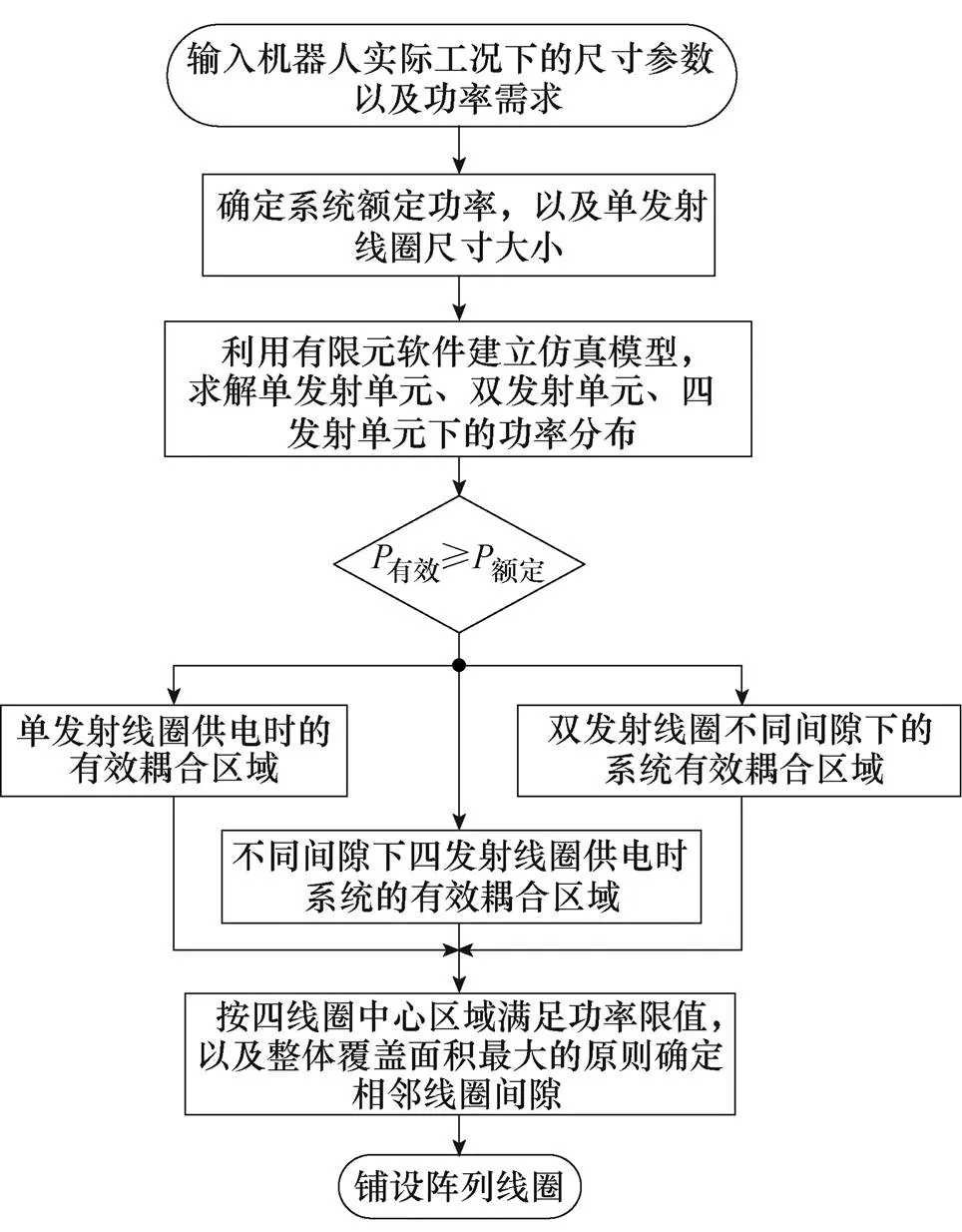
图13 阵列式发射模组结构设计流程

根据阵列线圈的设计流程和有效耦合区域分析结果，针对额定功率为50W的机器人，其动态无线供电系统的阵列发射线圈中相邻线圈间隙确定为35.66mm。下面以2×4阵列线圈结构中发射线圈Tx1～Tx4，阐述单发射线圈、双发射线圈以及四发射线圈三种激励模式的切换区域及流程，如图14所示。当接收线圈处于竖线阴影区域（单发射线圈中心为原点，半径为87.75mm的圆形）时，系统为单发射线圈供电模式；当接收线圈运动到横线阴影（以=68.34mm表征）时，系统为双发射线圈供电模式，其中接收线圈位于1横线阴影中范围内，则系统由发射线圈Tx1和Tx2同时供电，同理1、1、1横线阴影分别由发射线圈Tx1和Tx3、Tx3和Tx4、Tx2和Tx4同时供电；当接收线圈处于网格阴影区域时，系统由Tx1、Tx2、Tx3和Tx4同时供电。

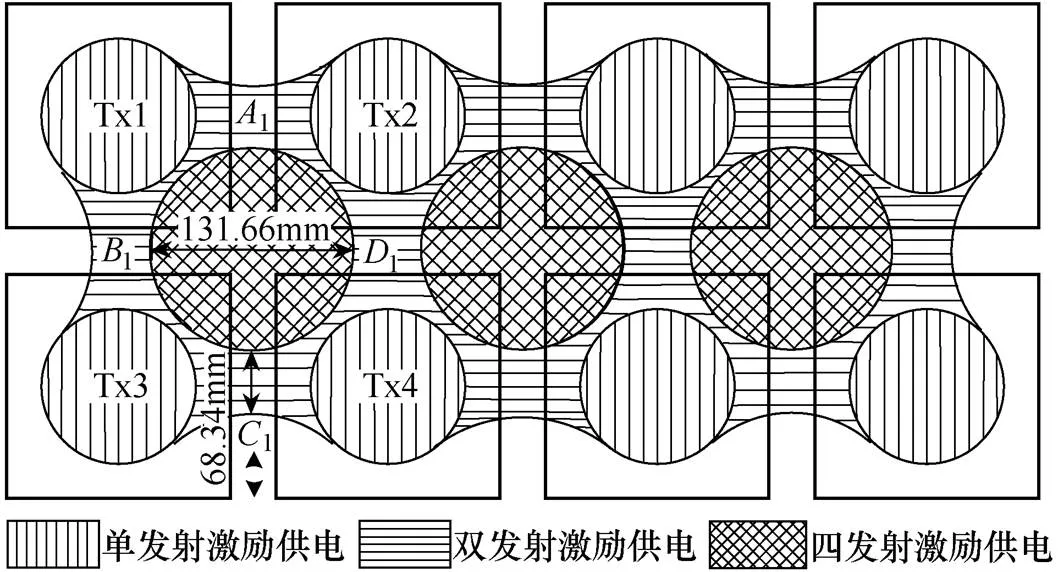
图14 阵列线圈工作模式切换区域

此外，由于以上对有效耦合区域的分析均基于单接收负载所得，因而在具体应用场景中，收发线圈动态耦合过程中每四个发射线圈单元上方规定只允许存在一个电能拾取接收负载。

4 实验研究

为验证采用有效耦合区域定量分析方法对阵列式电能发射模组空间结构排布设计的有效性，搭建了可模拟机器人不同运动过程的小型动态无线供电实验平台，通过上位机控制接收线圈的运动轨迹，测定接收功率不同位置处的波动，系统整体结构如图15a所示。系统发射端包括高频逆变电源、补偿网络以及2×2阵列发射线圈，系统配电采用市电作为共同母线的激励模式，逆变电源输出为85kHz的高频交流电，发射线圈单元外径为200mm，磁屏蔽采用相对磁导率2 800的铁氧体磁片拼接构成，如图15b和15c所示。

图15 动态无线供电系统实物

与仿真参数一致，实验过程中高频交流电源输出幅值s=100V，但由于实际线圈为手工绕制，线圈电感和寄生电容等参数与仿真系统中略有差异，进而导致实验结果与仿真结果存在区别，因此，需要通过实验修正单发射线圈、双发射线圈、四发射线圈供电系统在仿真研究中对有效耦合区域的定量分析结果，然后根据修正后的取值结果搭建阵列发射线圈，系统具体参数见表1。

表1 磁耦合机构系统参数

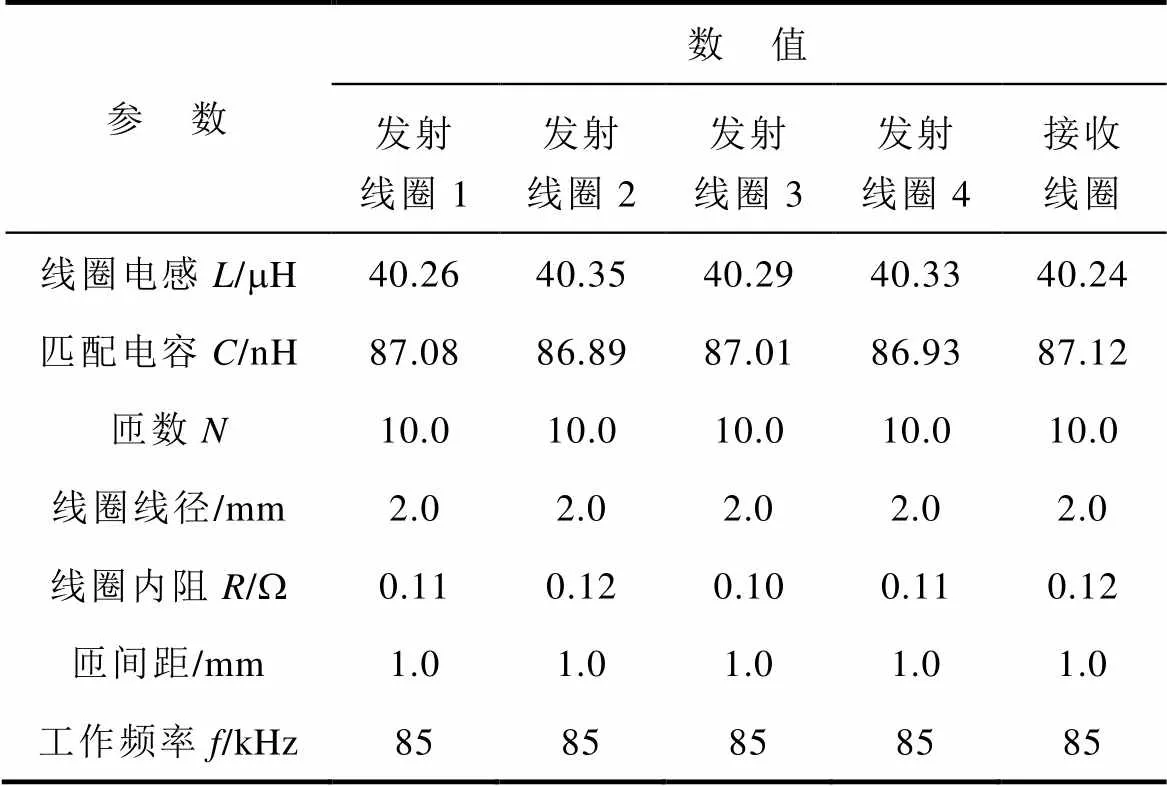
Tab.1 System parameters of magnetic coupling mechanism

4.1 有效耦合区域实验验证

当系统传输距离为100mm时，从仿真分析所得传输距离与有效耦合区域关系可知，其圆形有效耦合区域半径应为87.85mm。因而，参考仿真结果对实验内容做合理简化，将实验研究中接收线圈在轴偏移距离的范围选定75～95mm区间。

图16和图17为接收线圈运动中功率波动曲线和有效耦合区域随传输距离的变化曲线。由结果可知，实验结果比仿真结果略小，功率限值50W对应的偏移容忍距离为82.45mm。

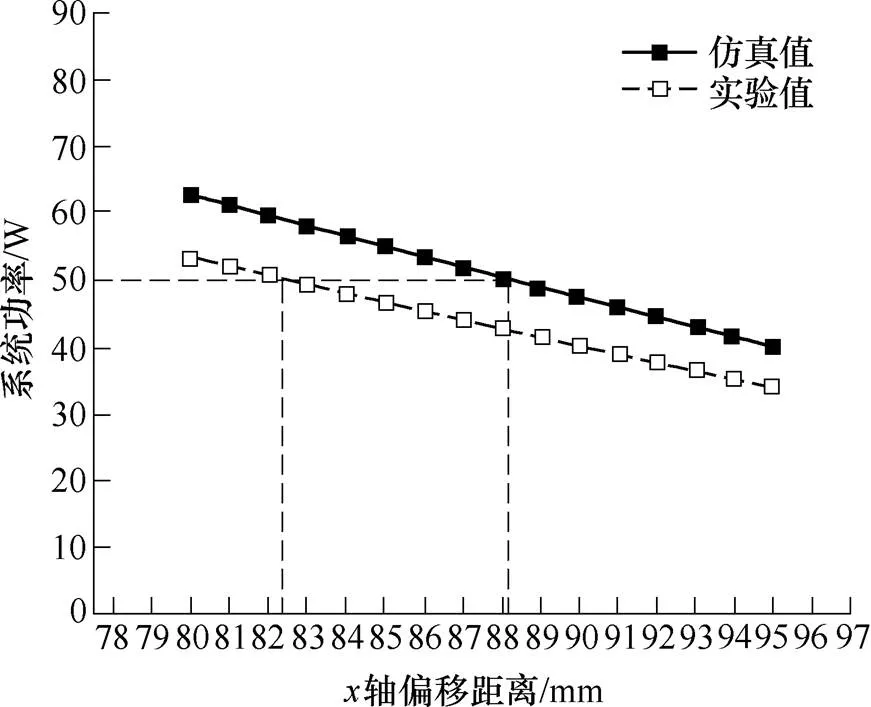
图16 单发射激励系统功率随偏移距离变化曲线

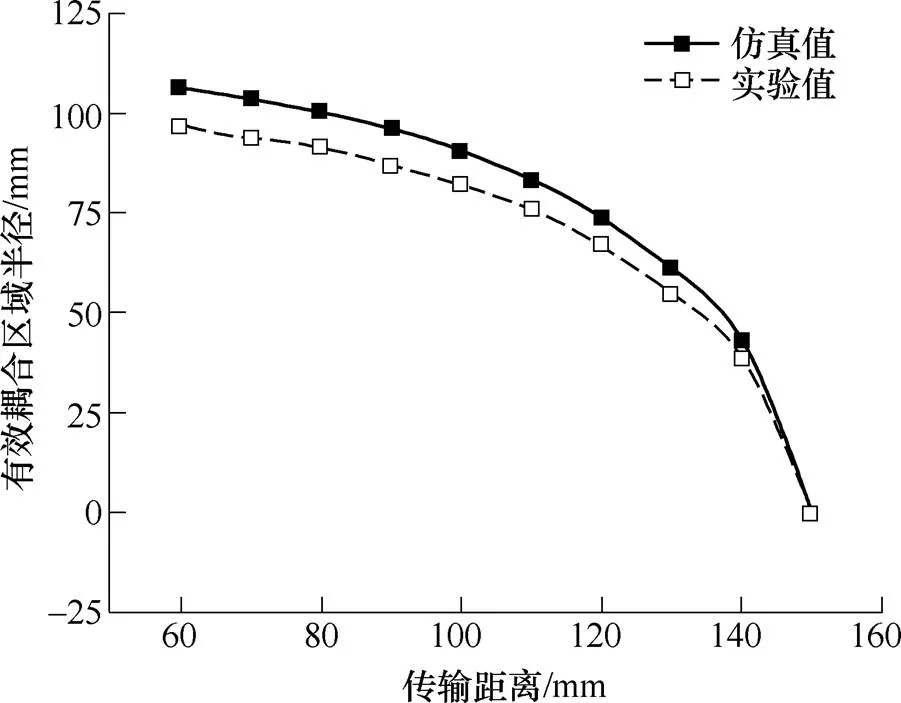
图17 传输距离与单发射激励系统有效耦合区域的关系

对于双发射线圈激励系统，由仿真分析结果可知，其有效耦合区域包括Ⅰ、Ⅱ类区域，其中Ⅱ类区域与发射线圈间隙的联系更为密切。因而，实验中主要研究双发射线圈间隙与系统有效耦合区域的关系，并通过Ⅱ类区域中值的变化表征其规律，双发射线圈间隙变化区间为[20mm, 50mm]。图18为双发射单元系统中线圈间隙改变时，其有效耦合区域中Ⅱ类区域中值的波动曲线。从图中来看，实验数据和仿真数据在变化趋势上具有较高的一致性，但在数值上略有差异。

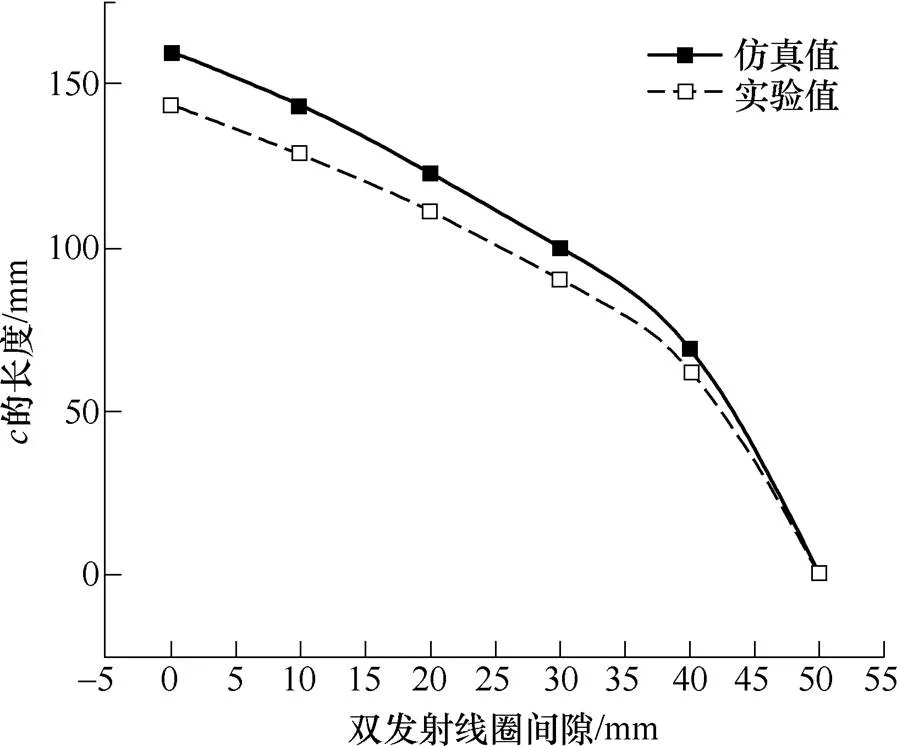
图18 线圈间隙与双发射激励系统有效耦合区域的关系

在四发射线圈供电系统，中心区域的功率波动数值决定了阵列线圈的排布间隙。实验中，四发射单元中的线圈间隙在20～40mm变化，接收线圈处于四发射线圈中心点的功率如图19所示。由结果可知，在系统功率为50W时，仿真中相邻发射线圈间隙应为35.66mm，实验结果为33.15mm。考虑到实验平台精度为1mm，在阵列发射线圈结构空间排布中的间隙应取33mm。

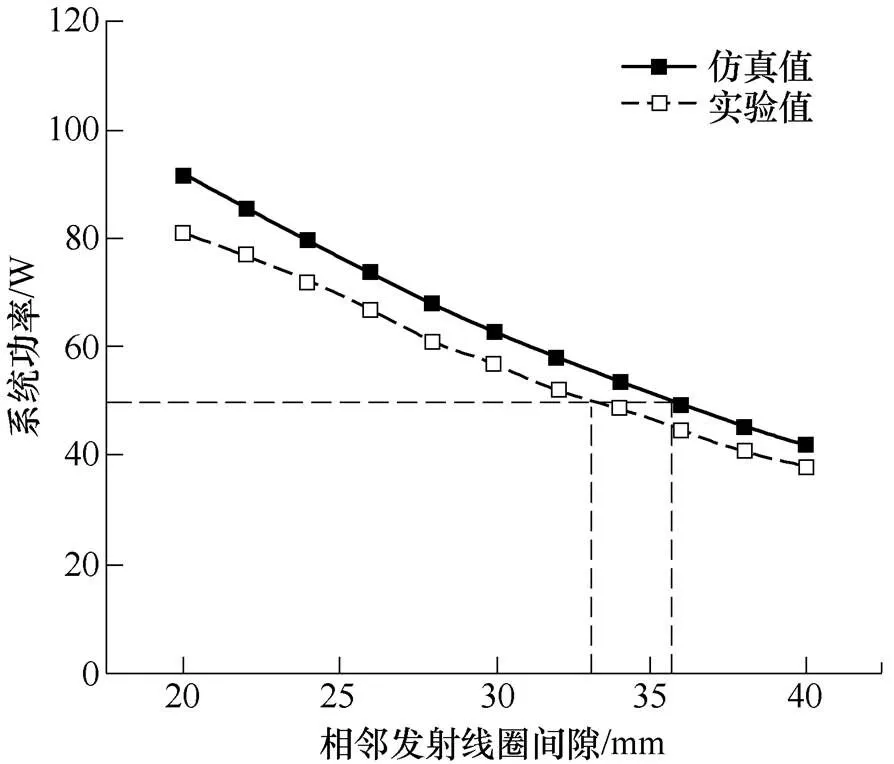
图19 相邻发射线圈间隙改变情形下功率变化曲线

4.2 阵列式发射模组工作模态实验

动态无线供电系统阵列发射模组按33mm的间隙排布，接收线圈工作模式切换工作区域与运动轨迹如图20所示，单发射线圈供电区域为半径82mm的竖线阴影区域，双发射线圈供电区域为横线阴影区域其特征值=64mm，剩余阴影区域为四发射线圈供电区域。为证明在该间隙下排布的阵列线圈，能够满足负载额定功率需求，在发射线圈上方任意位置均能正常工作。使接收线圈按图20中2—2—2路径移动，即从发射线圈2几何中心点2到发射线圈2和3间隙中点2，再到四发射线圈中心点2时，分析系统接收功率的波动情况，实验结果如图21所示。

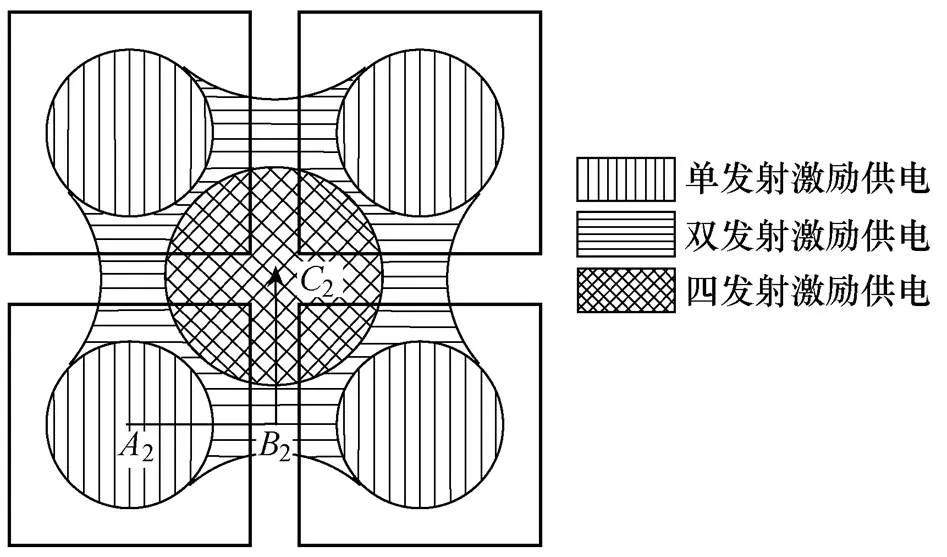
图20 接收线圈工作模式切换工作区域与运动轨迹

图21为接收线圈在2—2—2路径运动时系统的功率变化曲线。从图中可知，在接收线圈整个运动过程中，系统接收功率均大于负载额定功率，在发射线圈切换的临界点功率为50W，间隙区域通过双发射线圈或四发射线圈激励模式可有效补给负载的接收功率，使负载于任意位置均可靠获取电能，从而验证了本文设计的阵列发射模组根据负载位置，通过单发射线圈、双发射线圈和四发射线圈工作模式的切换为负载提供电能补给具有可行性。

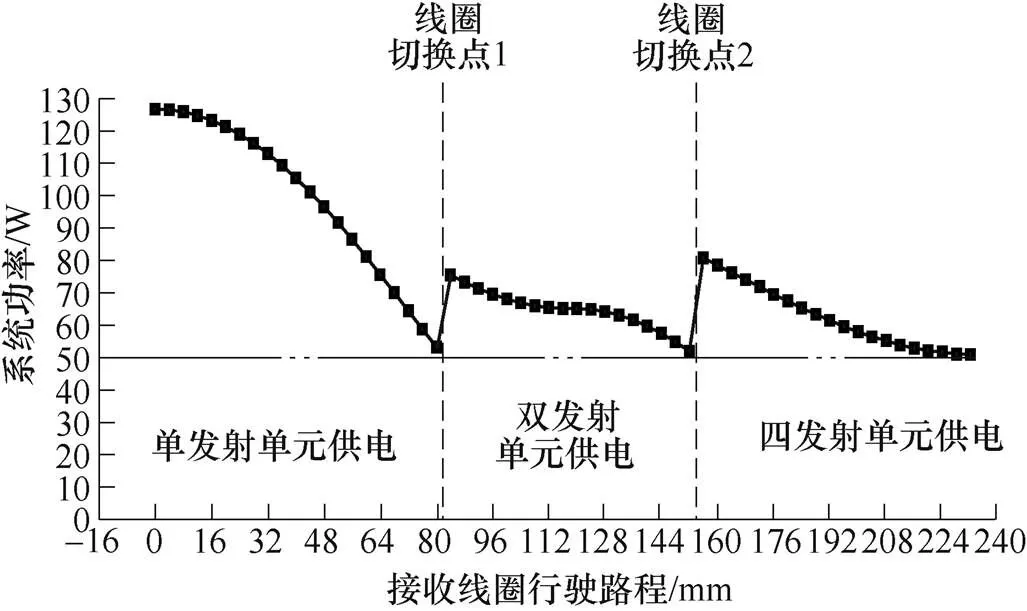
图21 接收线圈运动过程中的功率变化曲线

5 结论

本文基于机器人工作位置随机的特性，提出了基于有效耦合区域定量分析的动态无线供电阵列式发射模组设计方法，首先，分析了机器人工作过程中存在的三种耦合情形，同时理论推导了每种情形下的输出功率表达式。其次，以负载额定功率为基准，定义并划分了系统有效耦合区域，并利用有限元数值分析方法对三种激励模态下有效耦合区域进行了定量分析。再次，依据阵列式发射模组设计的需遵循的原则，给出了机器人动态无线供电系统阵列式发射模组的设计流程以及三种激励模式下的切换工作流程。最后，搭建了基于2×2阵列发射模组的小型动态无线供电实验平台，通过实验修正了仿真中有效耦合区域边界和阵列线圈排布间隙参数分析结果，进而验证了阵列式发射模组设计方案以及激励模态切换工作方法的有效性。结果表明，本文设计的阵列式发射模组结构能够实现机器人在随机位置动态无线补给电能的目的，可有效满足特定场景的实际应用需求。

在后续应用研究中，本文将以阵列式发射模组的结构设计为基础，从LCL和LCC等复合拓扑传输特性、机器人位置的精准定位、稳定性控制以及高效受电路径规划等方面进一步展开研究，从而完善机器人随机位置动态无线供电技术的理论研究体系，指导实际应用。

[1] 薛明, 杨庆新, 章鹏程, 等. 无线电能传输技术应用研究现状与关键问题[J]. 电工技术学报, 2021, 36(8): 1547-1568.

Xue Ming, Yang Qingxin, Zhang Pengcheng, et al. Application status and key issues of wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1547-1568.

[2] 贾金亮, 闫晓强. 磁耦合谐振式无线电能传输特性研究动态[J]. 电工技术学报, 2020, 35(20): 4217- 4231.

Jia Jinliang, Yan Xiaoqiang. Research tends of magnetic coupling resonant wireless power transfer characteristics[J]. Transactions of China Electro- technical Society, 2020, 35(20): 4217-4231.

[3] 沈栋, 杜贵平, 丘东元, 等. 无线电能传输系统电磁兼容研究现况及发展趋势[J]. 电工技术学报, 2020, 35(13): 2855-2869.

Shen Dong, Du Guiping, Qiu Dongyuan, et al. Research status and development trend of elec- tromagnetic compatibility of wireless power trans- mission system[J]. Transactions of China Elec- trotechnical Society, 2020, 35(13): 2855-2869.

[4] 王佩月, 左志平, 孙跃, 等. 基于双侧LCC的全双工无线电能传输能量信号并行传输系统[J]. 电工技术学报, 2021, 36(23): 4981-4991.

Wang Peiyue, Zuo Zhiping, Sun Yue, et al. Full- duplex simultaneous wireless power and data transfer system based on double-sided LCC topology[J]. Transactions of China Electrotechnical Society, 2021, 36(23): 4981-4991.

[5] 廖志娟, 孙跃, 叶兆虹, 等. 无线电能传输系统共振机理及共振点分布特性研究[J]. 电工技术学报, 2020, 35(2): 215-224.

Liao Zhijuan, Sun Yue, Ye Zhaohong, et al. Research on resonance mechanism and resonant point distribution characteristic of magnetic coupling wireless power transfer systems[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 215-224.

[6] 石黄霞, 付涛. 基于电磁耦合谐振的变电站巡检机器人无线充电研究[J]. 电子测量技术, 2019, 42(20): 40-43.

Shi Huangxia, Fu Tao. Study on charging of inspection robot in substation based on electro- magnetic coupling resonance[J]. Electronic Measurement Technology, 2019, 42(20): 40-43.

[7] Zhang Zhen, Pang Hongliang, Georgiadis A, et al. Wireless power transfer—an overview[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1044-1058.

[8] Campi T, Cruciani S, Maradei F, et al. Innovative wireless charging system for implantable capsule robots[J]. IEEE Transactions on Electromagnetic Compatibility, 2021, 63(5): 1726-1734.

[9] Sarin A, Avestruz A T. Code division multiple access wireless power transfer for energy sharing in hetero- genous robot swarms[J]. IEEE Access, 8: 132121- 132133.

[10] 崔志恒, 韩红玲. 红外导航自主充电室内移动机器人设计[J]. 实验室研究与探索, 2012, 31(10): 33-36.

Cui Zhiheng, Han Hongling. Design of an auto- recharging mobile robot navigated by infrared ray[J]. Research and Exploration in Laboratory, 2012, 31(10): 33-36.

[11] Zhao Peng, Cao Zhiqiang, Xu Lingyi, et al. The design of a mother robot for marsupial robotic system[C]//IEEE International Conference on Mecha- tronics and Automation, Tianjin, China, 2014: 675- 679.

[12] Sato I, Shinohara N. Study on antennas for wireless power transfer to in-line inspection robots[C]//IEEE Wireless Power Transfer Conference, London, UK, 2019: 292-296.

[13] Shidujaman M, Samani H, Raayatpanah M A, et al. Towards deploying the wireless charging robots in smart environments[C]//International Conference on System Science and Engineering (ICSSE), New Taipei, China, 2018: 1-6.

[14] Liu Han, Huang Xueliang, Tan Linlin, et al. Dynamic wireless charging for inspection robots based on decentralized energy pickup structure[J]. IEEE Transactions on Industrial Informatics, 2018, 14(4): 1786-1797.

[15] Anyapo C. Development of long rail dynamic wireless power transfer for battery-free mobile robot[C]//2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019- ECCE Asia), Busan, Korea (South), 2019: 1-6.

[16] 王伟嘉, 郑雅婷, 林国政, 等. 集群机器人研究综述[J]. 机器人, 2020, 42(2): 232-256.

Wang Weijia, Zheng Yating, Lin Guozheng, et al. Swarm robotics: a review[J]. Robot, 2020, 42(2): 232-256.

[17] 胡林林, 景凯凯, 袁顺刚. 一种巡检机器人无线充电发射端系统设计[J]. 电子元器件与信息技术, 2020, 4(7): 135-136.

Hu Linlin, Jing Kaikai, Yuan Shungang. Design of wireless charging transmitter system for patrol robot[J]. Electronic Component and Information Technology, 2020, 4(7): 135-136.

[18] Miwa K, Mori H, Kikuma N, et al. A consideration of efficiency improvement of transmitting coil array in wireless power transfer with magnetically coupled resonance[C]//IEEE Wireless Power Transfer, Perugia, Italy, 2013: 13-16.

[19] Jolani F, Yu Yiqiang, Chen Zhizhang. A planar positioning-free magnetically-coupled resonant wire- less power transfer[C]//IEEE Wireless Power Transfer Conference, Boulder, CO, USA, 2015: 1-3.

[20] 胡承. 基于阵列线圈磁谐振耦合的手机无线充电系统的研究[D]. 南昌: 华东交通大学, 2019.

[21] 刘柱. 基于阵列线圈磁耦合共振无线能量传输的研究[D]. 成都: 电子科技大学, 2018.

[22] Hui S Y R, Ho W C. A new generation of universal contactless battery charging platform for portable consumer electronic equipment[C]//IEEE 35th Annual Power Electronics Specialists Conference, Aachen, Germany, 2004: 638-644.

[23] Hui S Y R. Planar inductive battery charger[P]. UK patent application, 2002-06-10.

Optimal Design of Dynamic Wireless Power Transmitting Array Module in Random Position of Robot

1,21122

（1. State Key Laboratory of Reliability and Intelligence of Electrical Equipment Hebei University of Technology Tianjin 300401 China 2. Tianjin Key Laboratory of Electrical Equipment Intelligent Control Tianjin Polytechnic University Tianjin 300387 China）

Uninterrupted powering is the key to achieving intelligent swarmed or cargo-sorting robots. The paper proposes an optimized design for the transmitting array module based on the analysis of the effective coupling area, which meets the real-time power requirements of the robot at any position in the working area. Firstly, the paper analyzes the coupling situation of the transmitting and receiving coils during the robot operation, and the analytical expressions of the received power. Besides, a method defining the effective coupling area based on the robot's rated power demand is proposed. The effective coupling area under different excitation modes is quantitatively expressed using finite element analysis (FEA). Furthermore, the spatial structure arrangement of the transmitting array module and the corresponding coil excitation and conduction working mode are obtained. Finally, a scaled-down dynamic wireless power supply prototype based on 2×2 array transmitter modules is built to verify the effectiveness of dynamic wireless power supply for robots under any position.

Array transmitting module, dynamic wireless power supply, effective coupling region, coupling mechanism, robots

10.19595/j.cnki.1000-6753.tces.211611

TM724

国家自然科学基金面上资助项目（52077153）。

2021-10-11

2021-11-25

薛 明 男，1987年生，博士，研究方向为无线电能传输技术。E-mail: xueming@tiangong.edu.cn（通信作者）

杨庆新 男，1961年生，教授，博士生导师，研究方向为工程电磁场与磁技术。E-mail: qxyang@tjut.edu.cn

（编辑 崔文静）