变工况条件下汽轮机高压缸末级气动及强度性能研究

石红晖，王海波，曹蓉秀，姚力，晏鑫*

（1.国家能源集团科学技术研究院有限公司，江苏省 南京市 210046；2.西安交通大学能源与动力工程学院，陕西省 西安市 710049）

0 引言

对大中型火电机组进行供热改造，可以在不增加电力装机规模的前提下，发展热电联产集中供热，该措施既能解决分散小锅炉供热带来的能源、环境问题，又能满足日益增长的居民采暖和工业用汽需求[1-2]。然而，抽汽供热时主蒸汽流量的变化将对汽轮机高压缸末级的运行状态、气动性能以及叶片、轮盘等结构的强度造成一定影响[2]。因此，研究不同抽汽量工况下高压缸末级的气动和强度性能，对于汽轮机供热改造方案的制定以及热电联产机组在变工况条件下的安全、稳定、高效运行具有重要的指导意义。

目前，关于汽轮机供热改造变工况特性研究主要集中在小流量工况下低压缸的流动特性[3-5]，以及低压缸末级长叶片的强度和振动方面[6-8]。然而，与低压缸末级长叶片不同的是，由于高压缸叶片相对较短，叶片所受离心力和气动力的相对作用强度发生明显变化；且短叶片多采用T型叶根，其受力特点、结构强度与长叶片普遍采用的枞树型叶根差别较大[9-10]；另外，固定在动叶顶部的汽封结构也承受一部分气动力，而低压缸叶片的强度分析一般较少考虑汽封的影响。因此，研究带T型叶根、叶顶汽封的高压缸叶片在离心力、气动力作用下的应力状态和变形情况十分必要。

对于带T型叶根叶片的强度分析，部分学者进行了研究。Shankar等[11]建立了叶片-轮盘三维有限元模型，采用叶根与轮盘接触面节点完全匹配的六面体网格以提高计算精度，研究结果表明，在离心力的作用下，T型叶根进汽侧下倒圆处应力最大，叶型压力面根部的应力次之；其不足之处在于将叶根与轮盘视作完全紧密配合，忽略了二者之间非接触面的安装间隙。Gowda等[12]考虑了叶根与轮盘的实际配合间隙，采用旋转周期对称边界研究了整圈叶片的强度和疲劳特性，结果表明，叶根径向接触面圆角处等效应力最大且易出现疲劳损伤。文献[13-15]在T型、双T型叶根和叶根槽的结构设计和优化方面开展了较为充分的研究，对叶根和轮盘接触过程的有限元分析具有一定的指导作用。另外，Ehlers等[15]提出的精确适应复杂几何结构的多块六面体网格划分方法，对于提高有限元分析精度、节省计算资源都十分有利。然而，上述研究主要考虑离心力对叶片强度的影响，对叶片在三维流场中的受力情况以及变工况运行时的强度安全特性未进行深入研究。

为了研究变工况条件下高压缸末级的气动和强度性能，本文建立了带汽封结构的高压缸末两级计算流体动力学(computational fluid dynamics，CFD)计算模型，以及带外包T型叶根和叶顶汽封的末级动叶-轮盘的有限元分析(finite element analysis，FEA)模型，采用单向流固耦合[16]分析方法，对比了不同抽汽量(0%、8%、15%和20%)工况下高压缸末两级的总体性能和主要气动参数沿叶高的分布，分析了离心力和气动力对叶片−轮盘系统静应力和变形位移的影响机制，揭示了叶片、轮盘关键部位应力和叶顶最大变形位移随抽汽量的变化规律。

1 数值计算方法

1.1 CFD计算模型及方法

图1为带汽封结构的高压缸末两级(第11、12级)CFD计算模型，表1为叶栅和汽封的主要几何参数。由于两级动、静叶片数分别为64和80，故计算模型设置为4个动叶通道和5个静叶通道相匹配，使得动、静计算域周向宽度相同，从而其信息传递可以采用冻结转子法(frozen rotor)，以减小数值计算误差[17]。汽封与叶栅通道周向宽度保持一致，均为22.5°。

图1 高压缸末两级CFD计算模型Fig.1 CFD computational model for the last two stages in high pressure cylinder

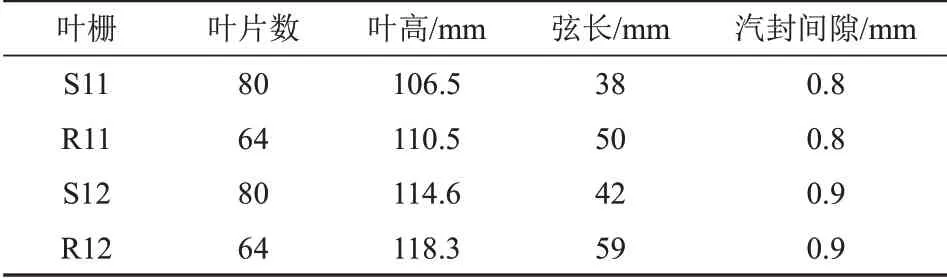
表1 叶栅和汽封的主要几何参数Tab.1 Main geometrical parameters for blades and seals

图2为叶栅和汽封的网格模型。利用商业软件NUMECA-AutoGrid5生成两级叶栅的结构化网格，网格最小偏斜角为28.9°；利用软件ANSYSICEM生成汽封的结构化网格，网格最小偏斜角为40.5°。叶栅和汽封近壁面第1层网格高度均为0.001 mm，网格节点总数约为5 073万。

图2 叶栅和汽封的计算网格Fig.2 Computational meshes for blades and seals

CFD计算模型的子午面视图如图3所示，其中：SD表示静止域；RD表示旋转域，其转速为3 000 r/min。表2为设计工况下CFD计算模型的边界条件。模型进口给定总温、总压，轴向进汽，中等湍流强度(5%)，出口给定平均静压。壁面采用绝热、光滑、无滑移边界，汽封中与轮毂面、动叶相连的壁面为旋转边界，转速为3 000 r/min；与围带面、静叶相连的壁面为静止边界；模型周向2个侧面采用旋转周期边界。动、静叶栅之间，以及汽封与主通道之间交界面的位置、编号如图3所示。动、静计算域(编号(1)—(11)所示)之间信息传递采用冻结转子法[18]。

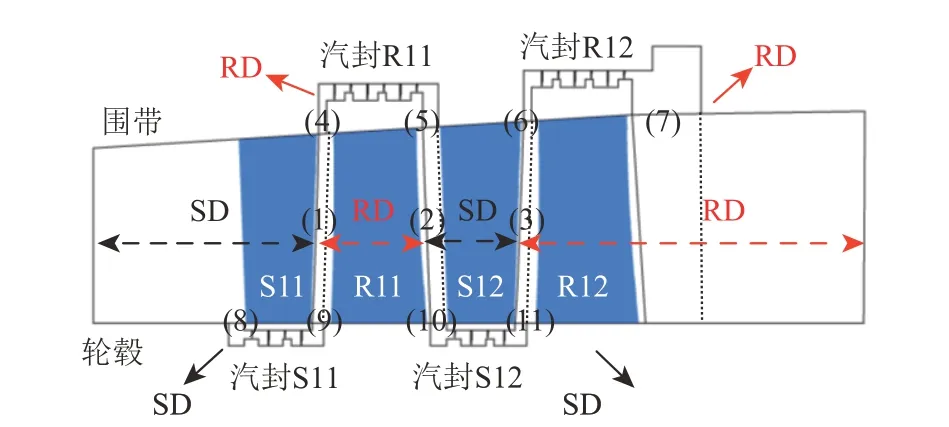
图3 CFD计算模型子午面视图Fig.3 Meridian view of CFD computational model

表2 CFD计算模型的边界条件Tab.2 Boundary conditions of CFD computational model

利用软件ANSYS-CFX求解三维定常RANS方程，模型工质为IAPWS-97标准的可压缩水蒸汽，湍流模型选用SST k-ω两方程湍流模型，控制方程离散采用高分辨率格式。当控制方程的均方根残差小于1×10−5，相邻迭代步出口截面平均温度波动小于0.01 K时，认为计算收敛。

为得到网格无关解，建立了5套近壁面第1层网格高度ywall的叶栅和汽封网格，采用动、静叶栅通道数为1∶1的单流道计算模型，研究了ywall对质量流量m和透平级总-总等熵效率ηit的影响，计算结果如表3所示。其中，透平级总-总等熵效率定义为

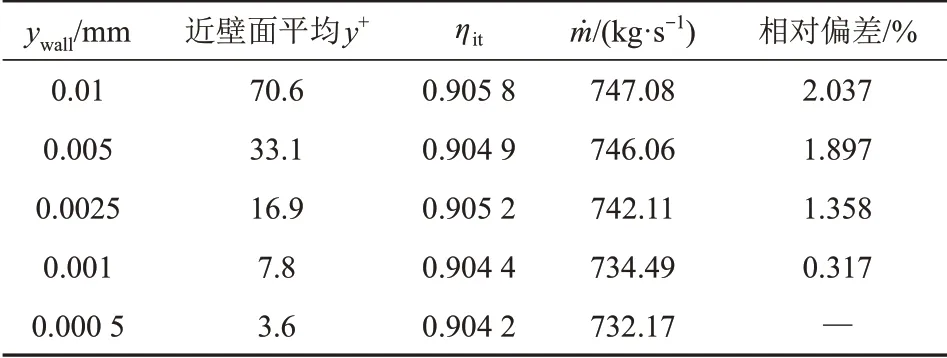
表3 近壁面第1层网格距离无关性分析Tab.3 Independency analysis of the first mesh layer distance near wall

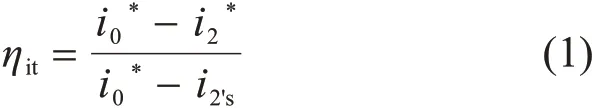
式中：i0*为透平级进口总焓；i2*为透平级出口总焓，i2's为透平级出口等熵静焓。

由表3可知，两级总−总等熵效率对ywall不敏感，而质量流量随ywall的减小而减小。当ywall由0.001 mm减小到0.000 5 mm时，流量变化已不再明显，故最终采用ywall=0.001 mm的网格，此时近壁面平均y+=7.8，满足SST k-ω两方程湍流模型的计算要求。

针对叶栅和汽封，研究了网格密度对m和ηit的影响，计算结果分别如表4、5所示。可见，网格密度对计算结果的影响不显著。最终确定叶栅和汽封网格节点数分别为710万和479万，即单流道网格总节点数为1 189万。

表4 叶栅网格密度无关性分析Tab.4 Independency analysis for grid density of blades

表5 汽封网格密度无关性分析Tab.5 Independency analysis for grid density of seals

1.2 FEA计算模型及方法

带外包T型叶根和叶顶汽封的高压缸末级动叶-轮盘FEA计算模型如图4所示。叶型高度为118.3 mm，叶型根部轮毂面半径为450 mm。取整周叶轮的1/64扇区进行单叶片的强度分析，模型周向宽度为5.625°。叶片和轮盘材料均选用2Cr13，其在400℃下的主要力学性能参数[19]如表6所示。由CFD计算结果可知，设计工况下高压缸末级动叶工作温度约为400℃，变工况时温度最高上升了约10℃。由于温度变化对材料的力学性能影响微小，故采用400℃下材料的力学性能进行计算，忽略温度变化引起的热应力对叶片强度的影响。

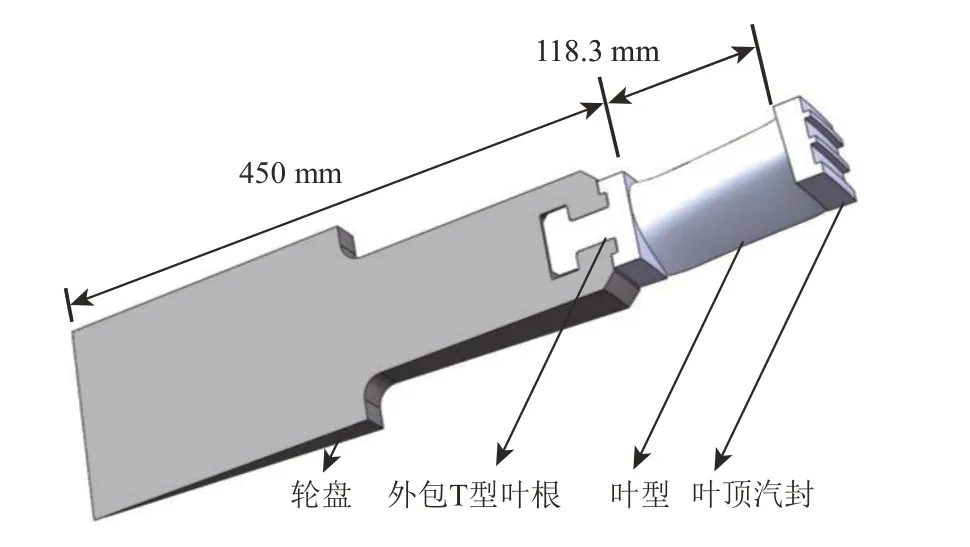
图4 高压缸末级动叶-轮盘FEA计算模型Fig.4 FEA computational model for the last stage rotor blade-disk in high pressure cylinder

表6 2Cr13在400℃下的主要力学性能参数Tab.6 Main mechanical property parameters of 2Cr13 at 400℃

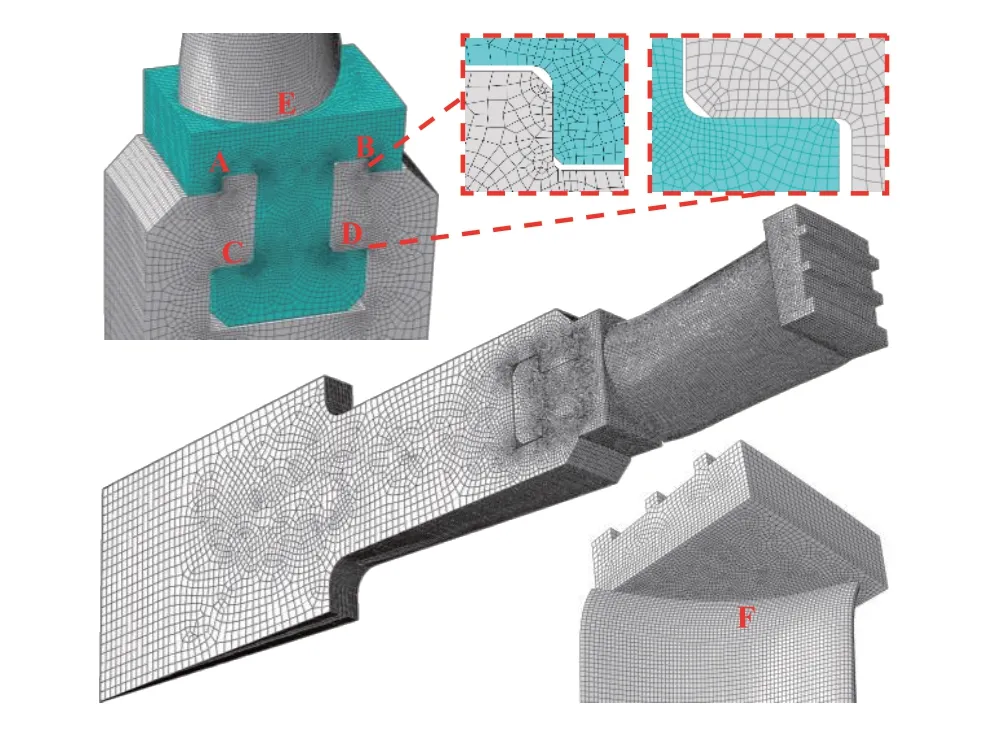
图5叶片−轮盘FEA计算网格Fig.5 FEA computational meshes for blade-disk

图5 为叶片-轮盘FEA网格模型。为了提高计算精度、节省计算资源，采用分块划分网格的方法，除轮盘轴线处存在少量楔形单元外，模型其余部位均为六面体单元；叶根与轮盘接触面(标号A、B、C、D)，以及叶根、叶顶汽封与叶型连接面(标号E、F)网格节点一一对应；对接触面附近和其他高应力区网格进行加密，最小单元尺寸为0.3 mm。由于CFD网格与FEA网格节点不完全对应，为了减小气动力耦合时带来的插值误差[16]，将气动力耦合面网格尺寸设置得尽可能小，最大单元尺寸为2 mm。计算单元采用适用于接触分析问题的C3D8I(8节点非协调线性六面体)单元，其总数为34.8万。

图6为FEA计算模型的边界条件及载荷。对轮盘旋转轴所在边线设置位移全约束，忽略主轴沿轴向的滑动，对轮盘主轴部分轴向2个侧面设置轴向位移约束。由于整圈叶片沿轮周方向安装，叶根、叶顶汽封处于互相挤压的紧密接触状态，故在叶根、叶顶汽封和轮盘的周向2个侧面设置切向位移约束。需要说明的是，由于单个扇区的气动力载荷沿周向分布不具有周期性，因此计算模型周向2个侧面无法采用旋转周期对称边界，而切向位移约束是相对合理的[12]。为了较为准确地模拟叶根与轮盘槽之间的相互作用，将轴向接触面A、B和径向接触面C、D设置为面面接触；接触特性设置为小滑移；接触面法向行为设置为硬接触，切向行为忽略摩擦作用[8]。对整个模型施加离心力载荷(如图6中绿色箭头所示)，角速度ω=100π rad/s。为了准确模拟叶片在三维流场中的受力情况，将CFD计算得到的叶型表面、轮毂面、围带面和叶顶汽封表面的气动力耦合到FEA计算模型上，4个部位的气动力载荷如图6中紫色箭头所示。

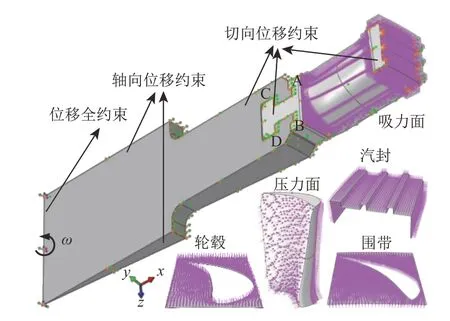
图6 FEA计算模型边界条件及载荷Fig.6 Boundary conditions and loads for the FEA computational model

2 计算结果分析

2.1 变工况透平级总体参数

表7为设计工况(0%抽汽)及抽汽量占设计工况总流量的8%、15%、20%工况下高压缸末两级总体参数。抽汽口位于高压缸次末级(第11级)进口处，忽略周向压力分布不均的影响。次末级进口总压Pin作为边界条件给定，随抽汽量的增大近似呈线性减小。各工况的进口总温和出口静压保持一致，分别为708.05 K和7.76 MPa。随着抽汽量的增大，出口总温Tout逐渐升高，20%抽汽量工况下Tout较设计工况上升了约10 K，高压缸末级叶片工作环境变差；两级输出功率P近似呈线性减小，20%抽汽量工况下P较设计工况降低了约44%。抽汽供热使高压缸末两级对外做功减少，从而影响机组运行的经济性。

表7 高压缸末两级变工况总体参数Tab.7 Overall parameters of final two stage variable conditions of high-pressure cylinder

2.2 变工况透平级主要气动参数

为了说明汽封泄漏引起的二次流对透平级气动参数的影响，图7给出了20%抽汽量工况下叶顶和叶根附近二次流的子午面流线。由图7(a)可知，汽封R11的泄漏流进入末级叶栅通道后对主流产生扰动并不断向后扩展，二次流影响范围为叶顶附近约20%叶高区域；汽封R12对末级流动影响较小。由图7(b)可知，汽封S11的泄漏流对后三排叶栅的流动均产生影响，发展到末级动叶时二次流影响范围为叶根附近约30%叶高区域；汽封S12与S11的泄漏流在末级动叶相互掺混，其影响范围为叶根附近约20%叶高区域。

图7 20%抽汽工况下汽封泄漏引起的二次流子午面流线Fig.7 Secondary flow meridian streamlines caused by steam steal leakage under 20%extraction condition

图8给出了不同抽汽量工况下两级总-总等熵效率ηit随相对叶高Hˉ的变化规律。对于第11级，ηit在30%叶高以上区域变化较为平缓，且随抽汽量的增大而减小，20%抽汽量工况下ηit较设计工况减小了约3%；30%叶高以下区域由于受汽封S11泄漏流的影响，曲线在20%叶高处出现极值点，透平级气动效率最差，且该极值点随抽汽量的增大逐渐向右下方移动，其原因是汽封泄漏量随主流量的减小而减小，使得二次流的影响区域缩小，效率最低点向叶根方向移动。对于第12级，在30%叶高以上区域，抽汽量较小时ηit与设计工况较为接近，20%抽汽量工况下ηit偏离设计工况较多；30%叶高以下区域由于同时受汽封S11和S12泄漏流的影响，曲线发生明显波动，且变工况时ηit严重偏离设计工况，10%叶高处最大偏离量约为3.8%。可见，抽汽供热对高压缸末两级的气动效率影响显著。

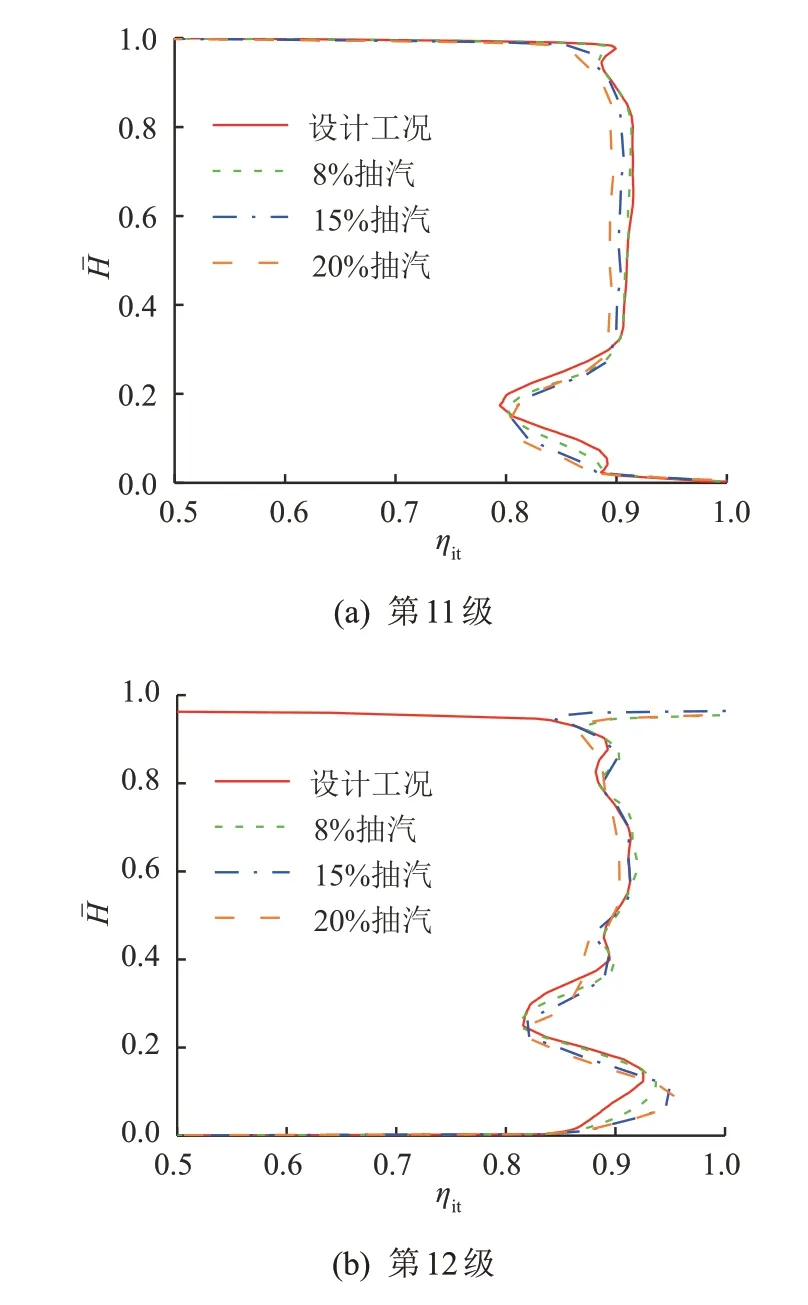
图8总-总等熵效率沿叶高的分布Fig.8 Total-total isentropic efficiency distributions along spanwise direction

图9 反动度沿叶高的分布Fig.9 Reaction degree distributions along the spanwise direction

式中：i1为动叶进口静焓；i2s为动叶出口等熵静焓。

由图9可知，在30%叶高以上区域，两级反动度Ω沿叶高方向逐渐增大，由于受汽封泄漏流的影响，叶根附近Ω出现波动。在第11级动叶50%叶高以下区域，Ω随抽汽量的增大而增大，20%抽汽量工况下Ω较设计工况最大增加了约0.9%；叶顶附近Ω几乎不受抽汽影响。第12级Ω沿叶高的分布呈现出类似的规律，但变工况时Ω偏离设计工况更为明显，20%抽汽量工况下Ω较设计工况最大增加了约1.6%，且该极值点也出现在20%叶高处。可见，抽汽供热对高压缸末级50%叶高以下区域的反动度影响较大，使得末级动、静叶栅焓降分配发生变化，从而影响机组运行的经济性和安全性[20]。

图10给出了不同抽汽量工况下两级叶栅出口汽流角随相对叶高Hˉ的变化规律。其中，静、动叶栅出口汽流角分别定义如下：

式中：Vz为绝对汽流速度轴向分量；Vt为绝对汽流速度切向分量；Wz为相对汽流速度轴向分量；Wt为相对汽流速度切向分量。

从图10可以看出，四排叶栅叶展中部汽流角变化较平缓，而靠近叶顶和叶根区域由于受汽封泄漏流的影响，汽流角发生明显波动，尤其是叶根附近。动、静叶栅30%~80%叶高区域汽流角基本不随抽汽量变化。除第11级静叶外，变工况时其余3排叶栅的叶顶和叶根附近出口汽流角明显偏离设计工况，且抽汽量越大，偏离越严重，尤其是20%和90%叶高处。20%抽汽量工况下第12级动叶20%叶高出口汽流角较设计工况最大增加了约2.4°。抽汽供热对高压缸末级叶栅出口汽流 角的影响大于前一级，且对动叶的影响大于静叶。叶栅出口汽流角的分布规律基本与图7所示二次流的影响范围相对应。与设计工况相比，抽汽工况下叶栅出口汽流角的变化容易引发较强的流动分离和尾迹涡，使流动损失增大、内效率降低[18]。

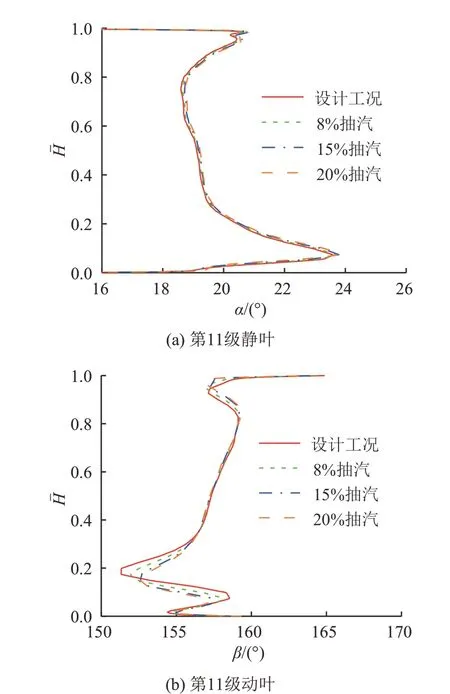
图10 叶栅出口汽流角沿叶高的分布Fig.10 Blade outlet flow angle distributions along the spanwise direction

2.3 离心力和气动力对叶片强度的影响对比

图11为离心力单独作用时叶片和轮盘的应力云图。由于整个叶片重心与轮盘中心线不完全重合，轮盘左右两侧应力分布并非完全对称，最大应力点位于叶根槽进汽侧倒圆(轮盘与叶根径向接触面C的根部倒圆)处，应力为428.9 MPa。相应地，叶片最大应力点位于叶根进汽侧下倒圆(叶根与轮盘径向接触面C的根部倒圆)处，该结果与文献[11-12]结论一致。叶根进汽侧下倒圆处的最大应力为423.3 MPa，约为出汽侧下倒圆处最大应力的1.3倍。叶型表面最大应力点位于压力面根部40%轴向弦长处，应力为286.6 MPa，而吸力面应力相对较小。由于材料屈服极限为735 MPa，故在离心力作用下叶片和轮盘强度满足要求，安全系数为1.74。

图11 离心力单独作用时叶片和轮盘应力分布Fig.11 Stress distributions in blade and disk with only centrifugal force

图12给出了设计工况下FEA计算模型中气动力耦合面的压力分布与CFD计算结果的对比。由图可知，FEA压力云图的色带边缘为锯齿状，这是气动力耦合面在数据传递中进行插值运算的结果[16]，可通过加密FEA模型中气动力耦合面附近的计算网格，以减小插值误差。总体来看，FEA计算模型中4个气动力耦合面的压力分布与CFD计算结果吻合良好。

图12 设计工况下FEA和CFD交界面上参数分布Fig.12 Parameter distributions on the interface between FEA and CFD domain under design condition

图13为设计工况下离心力、气动力作用时叶片和轮盘的应力云图。通过对比图11、13可知，气动力使叶片和轮盘进汽侧应力远远高于出汽侧，这是由汽流沿轴向的压力差所决定的。叶片最大应力点依然位于叶根进汽侧下倒圆处(该结果与文献[14]结论相一致)，应力为420.7 MPa，叶根槽进汽侧倒圆处的应力为379.5 MPa，二者较离心力单独作用时分别降低了约0.6%和11.5%。叶根进汽侧下倒圆处的最大应力约为出汽侧下倒圆处最大应力的3.4倍，而这一比例在离心力单独作用时仅为1.3；叶型压力面根部最大应力点位置基本不变，应力由286.6 MPa增大为289.1 MPa。由此可见，离心力对叶片主要产生沿径向的拉伸作用，而气动力对叶片主要产生沿轴向的弯曲作用，使叶片受力更不均匀；气动力的切向弯曲作用相对较弱。

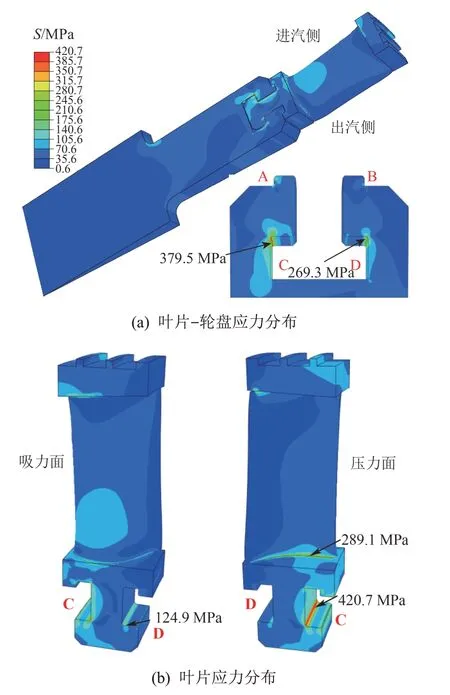
图13 离心力、气动力作用时叶片和轮盘应力分布Fig.13 Stress distributions in blade and disk with both centrifugal force and aerodynamic force

图14为加载气动力前后叶片变形位移云图(放大50倍)。无气动力作用时，叶顶最大位移为0.216 mm，主要为径向位移。加载气动力后，叶顶最大位移增大为原来的2倍以上，为0.443 mm，径向位移基本不变，而轴向位移明显增大。轮盘和叶根进汽侧位移明显大于出汽侧，叶型和叶顶汽封位移分布沿径向和轴向的变化速度均明显增大。由此可见，气动力对叶片变形位移影响显著，故在叶片强度分析中需同时考虑离心力和气动力的作用，且不能只关注最大应力的变化。

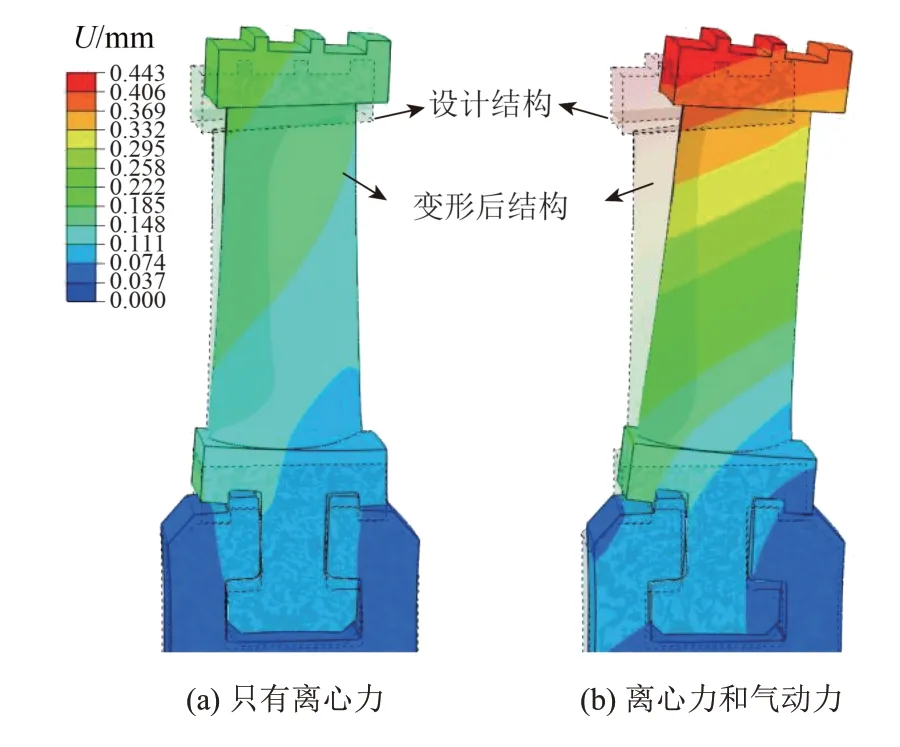
图14 加载气动力前后的叶片变形位移分布(放大50倍)Fig.14 Deformation displacement distributions of blade before and after loading aerodynamic force(magnify 50 times)

2.4 变工况末级动叶强度分析

图15 为叶片和轮盘关键部位高应力区的位置及编号，表8为不同抽汽量工况下相应位置的应力。可以看出，在离心力和气动力的作用下，叶根最大应力点位于进汽侧下倒圆处(位置⑤)；叶型表面最大应力点位于压力面根部40%轴向弦长处(位置②)；轮盘最大应力点位于叶根槽进汽侧倒圆处(位置⑥)，在0%、20%抽汽量工况下，位置⑥处应力较位置⑤处应力分别降低了10%、6%。随着抽汽量的增大，除了叶顶汽封与叶型吸力面连接处(位置①)的应力略微增大(不超过设计工况应力值的0.2%)之外，其余部位应力均近似呈线性减小；20%抽汽量工况下叶根最大应力较设计工况减小了约7.1%。

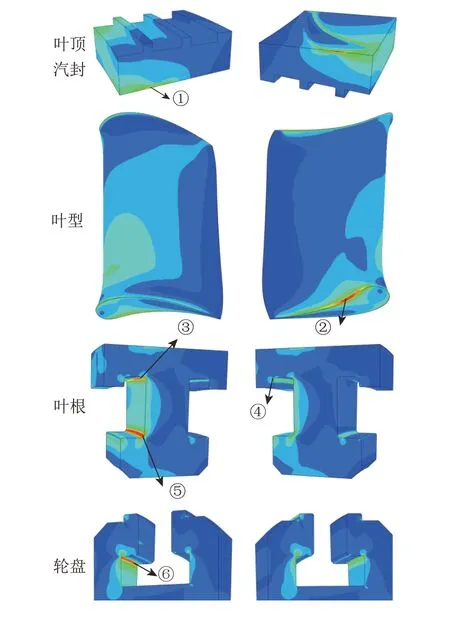
图15 叶片、轮盘高应力区位置及编号Fig.15 Position and number of high stress area in blade and disk

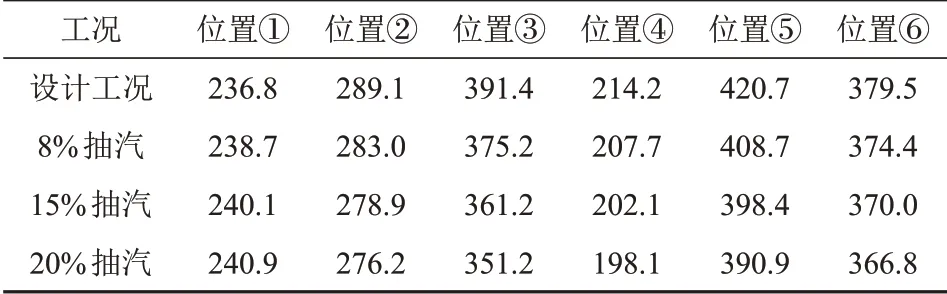
表8 变工况叶片、轮盘关键部位的应力Tab.8 Stress of key parts of blade and disk under variable conditions MPa

表9给出了不同抽汽量工况下叶片顶部最大变形位移。结合图14(b)可知，叶片变形位移沿叶高向上近似呈线性增大，且进汽侧位移明显大于出汽侧。叶片变形主要沿轴向和径向，径向位移主要由离心力的拉伸作用而产生，由于转速保持不变，变工况时叶片径向位移变化较小(不超过设计工况径向位移的0.3%)；轴向位移主要由气动力的弯曲作用而产生，由于末级动叶前后压力差随抽汽量的增大而减小，气动力的弯曲作用减弱，轴向位移随之减小。叶顶最大变形量随抽汽量的增大近似呈线性减小，20%抽汽量工况下最大变形量较设计工况减小了约19.2%。

表9 变工况叶片顶部最大变形位移Tab.9 Maximum deformation displacement of blade tip under variable conditions mm

3 结论

采用单向流固耦合分析方法，对4种抽汽量工况下汽轮机高压缸末级的气动和强度性能进行了数值研究，主要结论如下：

1）随着抽汽量的增大，高压缸出口总温逐渐升高，应注意末级叶片的运行安全；高压缸总−总等熵效率显著下降，输出功率随着抽汽量的增大而近似呈线性减小。

2）随着抽汽量的增大，叶片根部反动度逐渐增大，但叶顶反动度几乎不受影响；叶展中部汽流角变化较小，但叶顶和叶根区域由于受汽封泄漏流的影响而变化显著。

3）随着抽汽量的增大，除叶顶汽封与叶型吸力面连接处的应力略微增大外，其余部位的应力近似呈线性减小；叶根最大应力和叶顶最大变形量均随抽汽量的增大近似呈线性减小。