柔性直流接入海上风电并网选址综合优化

刘晓明，谭祖贶，袁振华，刘玉田*

（1.国网山东省电力公司经济技术研究院，山东省 济南市 250021；2.电网智能化调度与控制教育部重点实验室(山东大学)，山东省 济南市 250061）

0 引言

近年来，受气候变化导致的能源转型要求所驱动，海上风电发展更加迅速，2020年中国新增海上风电装机容量达到3.06 GW，位列全球第一[1-2]。2021年全球新增海上风电装机容量约19.5 GW，最大的贡献依然来自中国大陆，占4/5，约为16.9 GW。随着海上风电资源的逐步开发，更大单机容量、更大规模的海上风电场将是未来发展方向[3]。目前，海上风电场并网方式主要有高压交流输电和高压直流输电[4]。其中，高压直流输电方案比高压交流输电方案具有更大的优势，而高压直流输电方案中，基于柔性直流输电(voltage source converter high voltage direct current，VSC-HVDC)的并网方案与传统直流方式相比，具有灵活可靠的特点[5-6]，成为海上风电并网的研究热点。

随着海上风电场规模的不断增大，风电的消纳问题亟须解决，风电接入后的电网安全性也面临挑战[7-8]。不同的风电并网点对电网的影响也不同，选择合适的并网点对于风电消纳和电网安全稳定运行具有重要实际意义。文献[9]基于线路过载和功率灵敏度筛选柔性直流的接入点，但是未涉及风电并网内容。文献[10]以经济效益为优化目标，对经柔性直流接入的海上风电场和并联电容器组进行联合优化选址和选型，但未考虑风电功率波动影响。文献[11]针对交流接入的风电系统，利用小干扰稳定分析寻找对电网电压影响最小的风电并网点，文献[12]针对交流接入的大规模陆上风电，考虑有功需求、输电网络脆弱度、电力系统安全稳定性和经济性因素，选择合适的风电并网点，但是它们均未涉及柔性直流接入的海上风电。文献[13]针对经柔性直流接入的风电场，在陆上接入点选择时，充分考虑了电压源换流器(voltage source converter，VSC)换流站的电压支撑能力，但是未考虑电网消纳能力及电网强度问题。

针对目前大规模海上风电柔性直流并网选址研究较少、选址考虑因素不全面的问题，本文提出了一种经柔性直流接入的大规模海上风电场陆上并网点选择方法，并将该方法应用于某海上风电接入的山东电网进行仿真验证。

1 陆上并网点选择影响因素

1.1 海上风电消纳能力

2020年全国风电发电量为4 665亿kW·h，弃风电量约166亿kW·h，利用率达97%，但是风电发电量占全社会用电量比例仅约为6.2%[2]。考虑到“碳中和2060”的目标，风力发电的比重将大幅增长，大规模海上风电接入的消纳以及利用率情况成为必须考虑的问题。

对于不同的并网点，风电消纳能力主要考虑如下2个方面：一是系统调节和电网输送能力，具体是指并网点在短期内满足自身负荷需求的同时向外输送风电的能力，对于不同的风电并网点，负荷水平越高，向外输送风电的能力越强，其风电的消纳能力也就越强；二是电能需求，具体是指在一个长周期的时间范围内该并网点有功的消耗情况，将风电并入电能需求高的节点，可以缓解可能发生的电能短缺问题，并提高风电消纳水平。

1.2 受端电网电压稳定性

对于经柔性直流接入的海上风电场，其对电网电压稳定性的影响具体考虑如下2个方面。

1）VSC换流站的电压支撑能力

VSC换流器具有独立控制无功功率的特性，因此它可以用作具有大容量的无功功率补偿设备[14]，通过对VSC换流站的控制，可以有效支撑换流站附近电网电压[15]，进而提高接入区域的交流系统电压稳定性[16]。因此，选择合适的风电并网点，将会有效提高电网电压稳定性。

2）风电功率波动对受端电网的影响

海上风电场的出力随着风力的随机变化而动态波动，当风电功率出现较大变化时，由于潮流的改变，接入区域的电压也会随之波动[17]，甚至越限。当大规模风电接入电网时，风电渗透率提高，风电功率的波动可能会导致更加严重的问题。当风电场并入不同的电网节点时，由于电网结构不同，电网潮流不同，由风电功率波动引起的电网电压波动也就不同，因此，对于风电并网点的选择，风电功率波动影响是必要的考虑因素。

1.3 并网点脆弱度

目前，世界范围内发生的很多大停电事故是因为某些脆弱线路的退出而导致潮流转移，引起相继保护跳闸，从而发生连锁故障[18]，而其中多起又与风机大面积脱网有关。通过对电网节点的脆弱度分析可以评价电网安全等级，找到电网的薄弱位置[19]。在海上风电并网点选择时，应当对并网点进行脆弱度分析，并避免将风电场并入这些节点，以免因风电场的出力波动或者故障退出而导致严重的电网事故。

1.4 海上风电建设成本

在选择海上风电场并网点时，建设成本也是必要的考虑指标，对于不同的陆上并网点，海上风电场、升压站和换流站的投资是相同的，成本的主要区别在于海缆的长度不同。因此，在选择海上风电场并网点时，主要考虑不同并网方案的海缆长度。

2 评估指标计算

2.1 风电消纳

风电消纳的关键问题是系统的调节能力和电网输电能力[20]，具体而言，包括系统调峰能力、系统备用水平、电网网架约束与送出、负荷水平和风电出力特性[21]。在风电并网点选择研究中，由于接入区域范围不大，系统调峰水平与备用情况类似，因此主要考虑并网点送出能力及负荷水平等因素。

用电负荷与常规机组最小技术出力之间的运行区域是系统的调节空间，再加上经联络线最大外送功率，即为风电最大消纳空间[22]，同时为了考虑极限情况下最大风电消纳，假定并网点j负荷为日最小负荷Pj,Lmin，系统调节和电网输送能力指标计算如下：

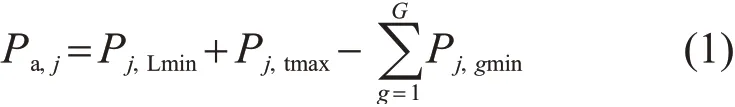
式中：Pa,j为并网点j的风电最大消纳空间；Pj,tmax为并网点j可以经联络线外送的最大功率；Pj,gmin为与并网点j相连的第g台常规机组的最小技术出力；G为与并网点j相连的所有常规机组的台数。

在对电能需求指标进行计算时，结合社会发展和中长期负荷预测[12,23]，对未来一段时期的负荷水平进行综合，获得并网点电能需求L(j)。

综合以上2个方面，并网点风电消纳指标C1计算如下：

2.2 电网电压稳定性

2.2.1 VSC电压支撑

VSC换流站对无功需求响应迅速且灵活，可以用来支撑接入区域电压[24]。出于经济性等因素的考虑，海上风电场的并网点选择方案一般都集中于一个范围不大的区域内，因此可以只考虑VSC换流站对该接入区域内母线电压的支撑能力。在假定海上风电出力为稳定值的情况下，可以将并网点视为电网的有功功率和电压给定节点(PV节点)。利用文献[25]中用于电网电压稳定性在线监测快速计算的简化L指标，计算不同VSC换流站位置对电网电压稳定性的影响。

将海上风电接入区域的节点分成2组：一组为所有发电机组节点集合αG；一组为所有负荷节点集合αL。简化L指标[25]可以计算如下：

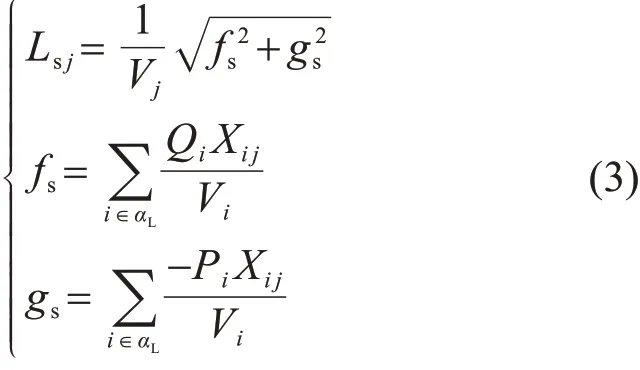
式中：Lsj为负荷节点j的简化L指标值，用于反映系统电压稳定程度，指标值越大，系统电压越不稳定，其取值范围为0≤Lsj≤1；Vi和Vj分别为负荷节点i和j的电压；Pi和Qi分别为负荷节点i注入的有功和无功功率；Xij为负荷节点i、j之间的电抗。

海上风电接入区域内简化L指标值最大的节点代表其电压稳定性最差，可以用来反映VSC换流站的电压支撑效果，因此接入区域VSC电压支撑指标C2计算如下：

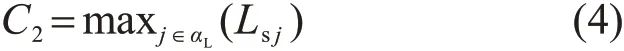
2.2.2 风电功率波动影响

评价风电并网引起的电网电压波动指标有电压分布指标、偏度指标、保持指数指标等[26]。在此基础上，本文主要考虑接入区域母线电压和风电出力波动情况，提出计及风电出力变化的母线i灵敏度Ii计算式[27]如下：

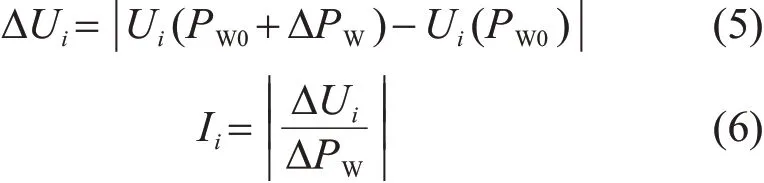
式中：PW0为海上风电场稳态出力；ΔPW为风电功率变化值；Ui(PW0+ΔPW)为风电出力为PW0+ΔPW时母线i的电压；Ui(PW0)为风电出力为PW0时母线i的电压；ΔUi为风电波动为ΔPW时母线i的电压变化值。

面对风电功率波动时，电压波动更大的母线节点因其越限的可能性相对较大，需要特别关注。同时考虑到大规模风电接入时，接入的输电网络一般电压等级比较高，可以认为接入区域电网母线电压最大波动在2%额定电压以内，该指标可视为合格，因此风电波动指标C3计算如下：

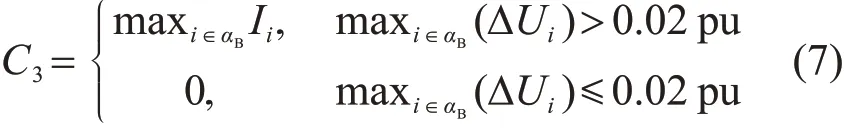
式中αB为接入区域母线集合。

2.3 电网节点脆弱度

电网节点脆弱度反映了其网络结构的重要性和鲁棒性，如果并网点脆弱度高，很可能因为风电场故障而破坏电网的安全稳定运行。对于风电并网点的脆弱度分析，可以从以下2个方面考虑：一是考虑并网点相连线路负载率，负载率越高，该并网点越脆弱；二是考虑并网点相连线路N−1故障情况下并网点电压偏差，偏差越大，该并网点越脆弱。

对于并网点j，假设线路Ik(k=1,2,…,mg)与其相连，该线路在风电并网前传输功率为Pk，且最大传输功率为Pkmax，则负载率指标计算如下：

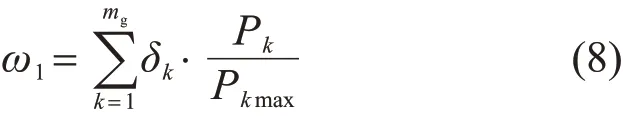
式中δk为权重系数。

假设线路Ik故障切除前后并网点j的电压分别为Uko和Uk，则N−1故障节点电压偏移指标计算如下：

本文综合考虑负载率和电压偏移，并网点脆弱度指标C4计算如下：

2.4 建设成本

对于不同的并网点选择方案，单位长度的直流海缆价格相同，因此建设成本指标C5可以计算如下：

式中：Lj是海上风电场与并网点j的直线距离；λj是在实际工程中海缆建设需要考虑的弯曲系数。

3 基于信息熵和模糊层次分析的综合赋权

信息熵主要用于描述信息源的不确定性，而熵权法是基于信息熵原理提出的用于客观评价指标权重的方法。如果评价指标的信息熵小，则代表其提供的信息量大，在系统评价时的权重占比也要大[28]。模糊层次分析法改进了层次分析法判断矩阵一致性检验和权重求取，主观评价指标权重。为了结合客观评价和主观评价的综合权重，弥补单一方法的不足，本文对2种赋权方法进行了集成。

假设海上风电并网点共有n个可选节点、m个评价指标，则可以建立一个数据矩阵：

式中r'ij为第j个可选并网点的第i个评价指标值，其中i=1,2,…,m；j=1,2,…,n。

综合权重的确定步骤具体如下：

1）原始数据的无量纲化和归一化处理。本文提出的指标中，C1指标值越大，节点越优；C2,C3,C4,C5指标值越小，节点越优。因此用式(13)处理数据矩阵R'，得到无量纲归一化数据矩阵R，使得数据在[0,1]内，且数据值越大，指标值越优。

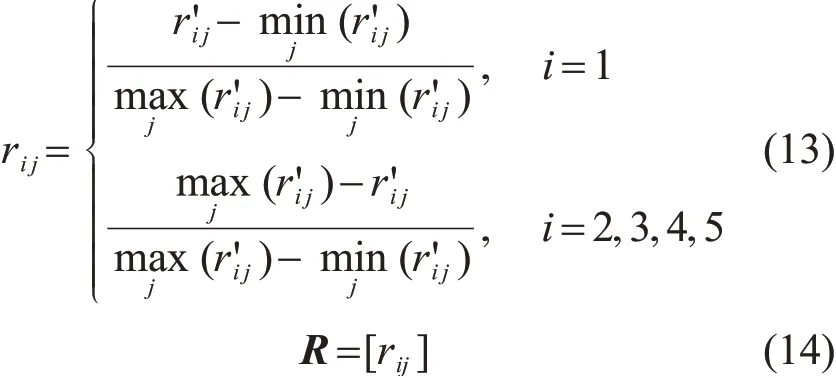
2）基于熵权法的客观权重计算。根据熵的定义，计算第i个评价指标的熵值如下：

且设定当fij=0时，fijln fij=0。

根据熵权法，第i个评价指标的权重表示为

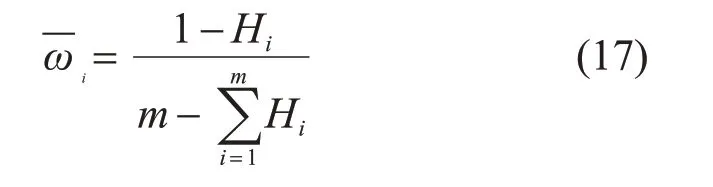
3）基于模糊层次分析的主观权重计算。假设对于并网点选择的m个指标，有如下模糊判断矩阵：

式中aij代表第i个评价指标比第j个评价指标重要的程度，0≤aij≤1，aij+aji=1，i,j=1,2,…,m，具体aij可以由“九标度法”表得到。

假设有s个专家基于“九标度法”表评价m个指标，并给出aij的标度值a(t)ij，t=1,2,…,s，aij可以计算如下：

式中λt为第t个专家评价的权重，且=1。

根据模糊层次分析法，主观权重计算如下：

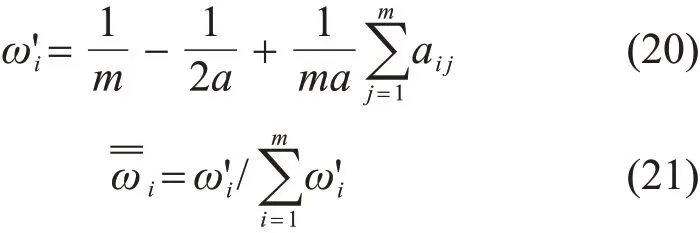
式中a≥(n-1)/2，为一常数，可以设a=(n-1)/2。

4）综合权重偏差最小的组合赋权。熵权法过于依赖客观的数据，但规划数据往往不充分；模糊层次分析通过专家的经验进行可行的判断，但难免带有主观片面性。综合上述2种方法，将会有效提高评价结果的准确性[29]。

由于本文仅涉及一个主观权重与一个客观权重，因此对矩估计理论的最优组合赋权法进行简化，以综合权重ωi与主、客观权重的偏差平方和最小为优化目标，设主观权重相对重要程度系数为α，客观权重相对重要程度系数为1-α，则优化模型表示为

不考虑0≤ωi≤1的约束，构造如下Lagrange函数：

式中λ为Lagrange乘子。

显然，求得的ωi满足约束条件0≤ωi≤1。

综上所述，经柔性直流接入的海上风电陆上并网点选择步骤具体如下：

1）根据接入区域电网运行数据及海上风电规划数据，结合潮流计算及仿真结果，利用式(1)—(11)计算不同海上风电并网点的各个指标值，并进行归一化处理。

2）基于各指标值，利用式(17)计算基于熵权法的指标客观权重基于模糊判断矩阵，利用式(20)、(21)计算基于模糊层次分析法的指标主观权重

3）利用式(25)得到各指标综合权重ωi，通过对不同并网点各指标值及其对应综合权重加权求和，得到不同并网点的综合得分，得分最高者即为最优的海上风电并网点。

4 仿真验证

4.1 烟台威海电网模型

为了验证所提海上风电场并网点选择方法的有效性，利用PSS/E对某风电场接入山东省东部沿海电网进行仿真分析。山东烟台、威海部分电网接线如图1所示，接入区域母线负荷如表1所示，规划建设的海上风电场位于黄海海域内。风电场额定容量为1 200 MW，经柔性直流接入。陆上VSC换流站容量为1 200 MW，直流输电的电压等级为±200 kV，可选并网点为6、9、13、14，其电压等级均为220 kV。

图1 山东省东部沿海电网接线图Fig.1 Wiring diagram of eastern Shandong coastal power grid

表1 山东东部部分母线负荷数据Tab.1 Load data of buses in eastern Shandong

4.2 最优并网点选择

风电消纳指标C1和建设成本指标C5不需要进行数值仿真，仅通过电网运行数据和风电场参数即可得到结果。

电压支撑指标C2、风电波动指标C3和电网节点脆弱度指标C4均需要通过PSS/E仿真计算得到结果。为不失一般性，假设风电场稳态出力为500 MW，在计算电压支撑指标C2时，将海上风电接入母线节点视为PV节点；在计算风电波动指标C3时，假设风电波动功率为300 MW。

标准化处理后各并网点指标值如表2所示，假定主观、客观权重的重要程度一致，均取0.5，计算得到各指标客观权重、主观权重以及综合权重，结果如表3所示。其中，专家评价模糊判断矩阵为

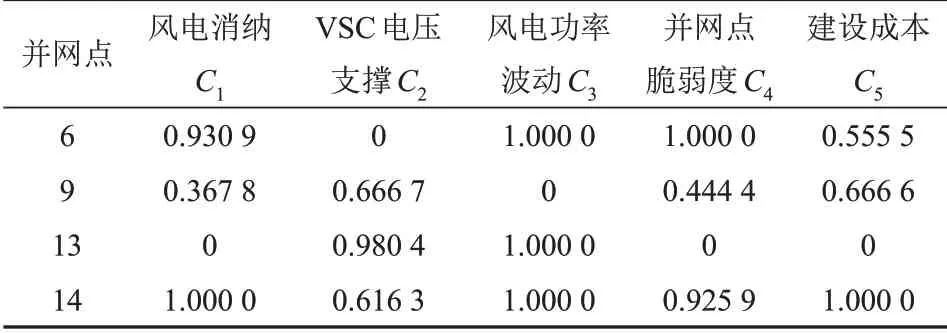
表2 标准化后各可选并网点指标值Tab.2 Index values of optional access points after standardization

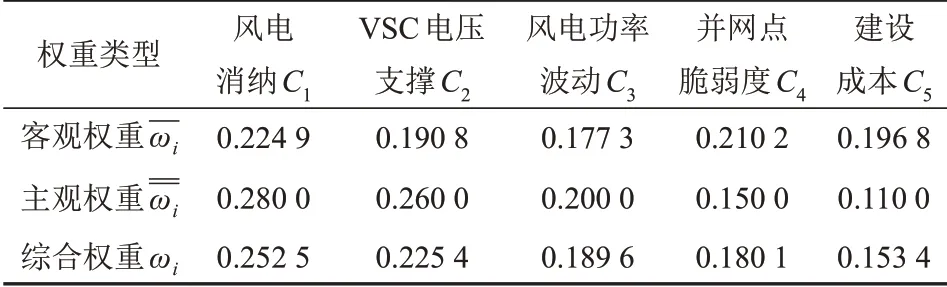
表3 各计算指标权重Tab.3 Weight of each evaluation index

基于指标值和综合权重，通过计算可以得到各并网点得分，如表4所示，可以看出，并网点14得分最高，为最优并网点。

表4 各并网点得分Tab.4 Score of each optional access point

4.3 最优并网点验证

1）风电功率变化对电网电压的影响

对于4个备选并网点，针对风电功率增加至额定满出力的情景进行仿真，记录接入区域电网中220 kV母线电压波动平均值与最大值，结果如表5所示。

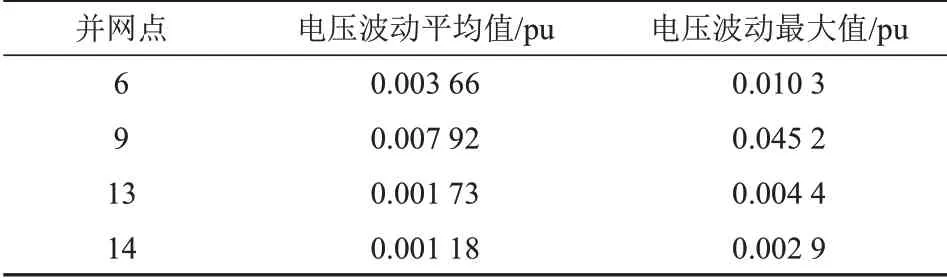
表5 电压波动结果Tab.5 Results of voltage fluctuation

根据表5中数据可知，当并网点为14时，接入区域电网电压波动平均值与最大值均最小，与本文方法计算的结果相符。

2）故障后电网电压情况

对于4个备选并网点，分别在选出的关键故障情况下仿真，记录接入区域电网电压变化情况，并进行对比分析。支路1—2的500 kV三相接地故障发生在靠近母线1的一侧，故障发生0.1 s后切除线路，其典型母线的电压变化曲线如图2所示。支路3—13的220 kV三相接地故障发生在靠近母线13一侧，故障发生0.1 s后切除线路，母线10的电压情况如图3所示。

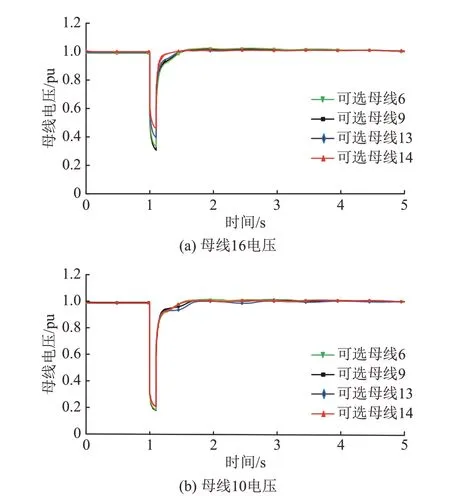
图2 1—2支路500 kV线路故障下典型母线电压Fig.2 Typical bus voltage of 1-2 branch 500 kV line fault

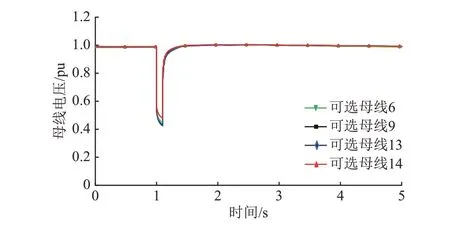
图3 3—13支路220 kV线路故障下母线10电压Fig.3 Bus 10 voltage of 3-13 branch 220 kV line fault

从图2可以看出，当并网点为14时，在故障发生后，典型母线的电压最小值更大，在切除线路后，典型母线的电压恢复更快且更稳定。由图3可知，严重程度低一些的故障，如220 kV线路接地故障，当并网点为14时，其对电压的支撑相比于其他并网点仍稍有优势，但是并不明显，主要是因为该故障对接入区域的电压影响没有500 kV三相接地故障大。

综合以上2个因素，并考虑到在风电消纳能力、建造的经济性上并网点14同样是最优的方案，这与计算得到的评价得分相符，证明该选择方法有效。

5 结论

针对经VSC-HVDC接入电网的海上风电场并网点选址，在考虑并网的经济性与安全稳定性的基础上，提出了基于信息熵理论和模糊层次分析法的综合评价方法，并进行了仿真分析，得到以下结论：

1）通过分析计算不同并网点的系统调节与输送能力水平及电能预期需求，保证了风电并网点的消纳能力，保障了大规模海上风电的高效利用，提高了风电并网的经济性。

2）考虑VSC换流站的电压支撑能力，有效利用了柔性直流输电方式对受端电网的无功支撑；考虑风电功率波动对电网电压的影响和并网点的脆弱度问题，降低了风电并网后其波动性对电网的影响，提高了受端电网的安全稳定性。

3）所提出的柔性直流接入海上风电场并网选址方法，可以为未来大规模海上风电并网选址提供理论指导。对于多个海上风电场接入同一区域电网的并网点选择问题，需要进一步研究。