易逝品在线销售数据的稀疏性问题及处理
吴宇平 李 磊
(新疆财经大学统计与数据科学学院,新疆 乌鲁木齐 830000)
一、引言
随着互联网和大数据技术的高速发展,数据量迅猛增长,数据形式越来越多样化。其中,稀疏数据这一特殊形式的数据成为研究者越来越关注的话题。稀疏数据绝对不是无用的数据,只是信息不完全的数据,通过适当的技术方法,可以从中挖掘出所需的有效信息[1]。
稀疏数据广泛存在于各种应用场景中。应用场景不同,稀疏数据表现出的特点不同,适用的稀疏性处理方法也不同。根据数据表现出的特点,可将稀疏数据分为三种类型:
第一种类型的稀疏数据指由于某些原因导致其中一部分数据值缺失的数据,也称为缺失数据[2]。例如,在数据收集的过程中,采用不恰当的观测手段或录入数据时发生错误,导致在问卷调查、医学研究、社会经济研究及其他科学研究中经常会出现数据缺失的现象,使信息被遗漏。Tutz 和Ramzan(2015)[3]针对高维的缺失数据,提出了基于距离的加权最近邻插补法。针对缺失数据较多的情况,Silv 和Perera(2016)[4]提出了进化KNN 插补法。Galan 和Lasheras 等(2017)[5]基于遗传算法,提出适用于测试和问卷的缺失数据处理方法。
第二种类型的稀疏数据指数据本身不存在缺失,但可利用的有效数据不足[6]。例如,在亚马逊或YouTube的推荐系统中,产品数量非常庞大,但网站上较活跃的用户群只对其中不到1%的产品有过消费记录,所以推荐系统可利用的消费记录数据非常稀少。数据的稀疏性问题会对推荐结果的准确性产生影响。对此,王喜智[6]提出了结合巴氏距离与雅克比距离的稀疏数据用户相似度模型,以提高推荐质量。在商品的最优定价研究中,针对历史销售数据中可利用的有效数据点较少的问题,Bauer 和Jannach(2018)[7]采用BootStrap 和核回归相结合的稀疏性处理方法来估计一个价格点是否是最优的概率。
第三种类型的稀疏数据指具有稀疏分布特性的数据,即数据的分布是稀疏的。例如,大气腐蚀数据的分布是严重稀疏的,其绝大部分数据集中在ISO 9223:1992(E)中少数等级上,数据分布严重不均,李志平和付冬梅等(2016)[8]针对大气腐蚀等级数据的稀疏分布特性,提出了一种基于稀疏数据归约的CMAC大气腐蚀数据补偿方法。李稳和刘伊克等(2016)[9]针对井下微震监测数据的稀疏分布特征,提出将图像处理领域适宜稀疏分布信号降噪处理的稀疏码收缩方法应用于井下微震监测数据处理。时空数据的稀疏分布是当前大数据挖掘面临的普遍问题,程诗奋和彭澎等(2020)[10]针对地理时空数据的稀疏分布特性,提出了时空数据重构解决方案。
在电子商务领域,受季节、特殊节日、需求不确定性以及商品自身特性等多种因素的影响,收集到的易逝品在线销售数据常常具有稀疏性,给易逝品的定价研究带来一定困难。为了从易逝品在线销售数据中挖掘出关于最优价格的有效信息,为易逝品定价提供决策支持,本文围绕易逝品在线销售数据的稀疏性问题展开研究,根据易逝品在线销售数据表现出的稀疏性特点,将适宜于此类稀疏性问题处理的BootStrap 和核回归相结合的方法应用于易逝品在线销售数据处理。
二、易逝品在线销售数据的稀疏性问题
为展现易逝品在线销售数据的稀疏性,本文选用李磊和宋建伟(2020)[11]使用的数据集中的部分数据,并对其进行描述性统计分析。该数据集是大枣、葡萄干、巴旦木3 种新疆特色农产品的相关数据,主要通过Python 网络爬虫程序和人工抓取相结合的方法从淘宝和天猫平台获得。从2018年4月6日到2018年10月27日,每3 天收集一次数据,共69 个观测时点。
本文选取规格为500g 的大枣作为研究对象。首先,选取该规格大枣的观测时间、销售价格和销售量3个变量;其次,用销售价格乘以相应的销售量得到销售收入,由于数据集中各销售量观测值指的是近30 天的销量,故这里计算得到的各销售收入值也是近30 天的收入;最后,将该易逝品的销售价格、观测时间(即销售价格保持不变的时长)、销售量、销售收入4个变量对应的共2546 条数据作为本文的数据集,该数据集中各变量的描述性统计见表1。

表1 数据的描述性统计
由表1可知,销售价格在11.80—49.90 元之间变动;销售价格保持不变的时长在9.00—204.00 天之间变动,销售价格保持不变的平均时长为85.92 天,中位数为85.50 天,其平均值和中位数均接近3 个月。
图1是各销售价格保持不变的时长的频数分布直方图,横坐标表示销售价格保持不变的时长,纵坐标表示频数,可以看出,各销售价格保持不变的时长长短不一,最长的时长达到了204 天。由于易逝品的价值会随时间的增加逐渐减少,从而导致消费者的购买欲望下降,因此易逝品销售价格的变动相较于其他商品理应更为频繁,即随着时间的增加,商家可适当调整销售价格,以适应不断变化的市场需求,实现利润最大化。但从表1和图1可以看出,本文研究所选取的易逝品的在线销售数据具有价格长时间保持不变的特点,即价格变动并不频繁。若要对某商家的商品进行动态定价研究,可利用的价格数据点较少,该特点与第二种类型稀疏数据的特点一致。

图1 销售价格保持不变的时长的频数分布直方图
图2是销售价格-平均销售收入散点图,横坐标表示销售价格,纵坐标表示平均销售收入,销售价格对应的平均销售收入指该价格保持不变的时长内,所观测到的销售收入的平均值。图中水平虚线代表所有销售价格对应的平均销售收入的均值,从图中可以看出:大部分的点分布在虚线附近,平均销售收入随销售价格变化的趋势和规律并不明显。表现销售价格如何影响平均销售收入的有效数据点较少,该特点与第二种类型稀疏数据的特点一致。
从图2还可以看出,区间(10,20)内有16 个价格点、区间(20,30)内有18 个价格点、区间(30,40)内有13 个价格点,而区间(40,50)内只有3 个价格点。(10,20)、(20,30)、(30,40)3 个区间内的价格点数量较为接近,均在10 以上,而(40,50)内的价格点数量与前3 个区间相比差距较大,且区间(10,20)、(20,30)、(30,40)内的点较密集,而区间(40,50)内的点非常稀疏。参考李志平和付冬梅等(2016)[8]的研究,在区间大小相同的情况下,各区间内的数据点数量相差大,且分布不均,稀疏密度差距大,说明数据是稀疏分布的,故本文研究所选取的价格数据是稀疏分布的,该特点与第三种类型稀疏数据的特点一致。

图2 销售价格-平均销售收入散点图
三、易逝品在线销售数据的稀疏性处理方法
针对易逝品在线销售数据表现出的稀疏性特点,本文采用BootStrap 和核回归相结合的方法处理易逝品在线销售数据的稀疏性问题。首先,运用BootStrap方法计算各离散价格点对应的BootStrap 置信度;其次,运用核回归方法对离散价格点的BootStrap 置信度进行拟合,从而得到整个定价区间上连续价格水平与其对应的BootStrap 置信度之间的非线性函数关系。由于每个价格水平对应的BootStrap 置信度可作为该价格水平是最优价格的概率估计,故对易逝品在线销售数据进行稀疏性处理后,可初步得到定价区间内任意价格水平是最优价格的概率估计值。
(一)离散价格点的BootStrap 置信度计算
BootStrap 方法是统计学中一种重要的非参数估计方法,该方法在数据分析方面有着广泛应用。BootStrap方法的基本思想是在原始数据基础上进行有放回抽样,从而产生一系列样本量相同的BootStrap 样本,并利用这些样本对总体进行推断。当数据分布未知或样本容量较小时,BootStrap 方法仍然是有效的。BootStrap方法的具体步骤为:假设一个数据样本的总体分布F未知,但已知有一个来自分布F 的数据样本D,其样本容量为N,从该样本中进行有放回的抽样,抽取后样本容量仍为N。相继独立地从原始样本中抽取多个BootStrap 样本,然后利用这些样本对整体进行统计推断[12]。
假设真实观测到的售价集合为{pn|n=1,2,…,N},Hn表示真实销售价格pn保持不变的时长;Rn1,Rn2,…,Rnk表示在时长Hn内,售价pn所对应的k 个真实观测到的日销售收入;Rn=(Rn1+Rn2+…+Rnk)/k 表示在时长Hn内,售价pn对应的日平均销售收入。现用R%表示事先设置的阈值,根据Bauer 和Jannach(2018)[7]的研究,可使商家获得最大利润的价格称为最优价格,若要对售价pn是最优价格的概率进行估计,可运用非参数BootStrap 方法计算pn所对应的Rn值大于或等于阈值R%的BootStrap 置信度Cn。Cn的值即为pn是最优价格的概率估计值,可表示为:

由于BootStrap 置信度Cn描述了真实销售价格pn是最优价格的概率,故Cn越大,越有理由认为pn是最优价格。
对于阈值R%,最直接的选择方式是由于商家在销售的过程中,可能会采取一定的促销手段销售商品,从而使某一时间段内的销量突增,这就会导致该时间段内收入的最大值偏离正常水平,从而影响阈值的大小,过高的阈值可能会导致Cn的估计结果为0,故可适当降低该阈值。参考已有研究对阈值的取值方法,可将阈值R%设置为的90%分位数。
下面对BootStrap 置信度Cn的计算步骤进行说明,具体步骤如下:
①首先设定抽样次数W,每次抽样的样本数据量为Dn,对Rn1,Rn2,…,Rnk进行反复W 次有放回抽样,得到W 个BootStrap 样本,将每次抽样后得到的BootStrap 样本中的Dn个数据记为R'n1,R'n2,…,R'nk。
②对每一个BootStrap 样本,计算其Dn个数据的均值,如式(2)所示:

③统计W 个BootStrap 样本中均值大于或等于阈值R%的样本数量,记为Xn,则Cn的计算公式如式(3)所示:
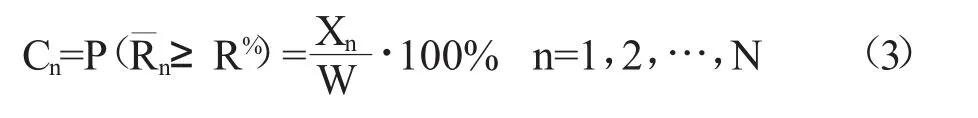
④对{pn|n=1,2,…,N}中的每一个销售价格,均按照步骤①、②、③计算其对应的BootStrap 置信度,则可得N 个BootStrap 置信度,即C1,C2,…,CN。
(二)基于核回归的BootStrap 置信度拟合
Nadaraya 和Watson 于1964年提出了著名的Nadaraya-Watson 核估计。由于Nadaraya-Watson 核估计有且仅有一个参数,相较于其他参数较多的估计方法,该方法不易发生过拟合。
本文使用Nadaraya-Watson 核估计对上一节中的BootStrap 置信度C1,C2,…,CN进行拟合,目的是得到连续价格水平与其对应的BootStrap 置信度之间的非线性函数关系。对给定的核函数K,其Nadaraya-Watson核估计定义如下:
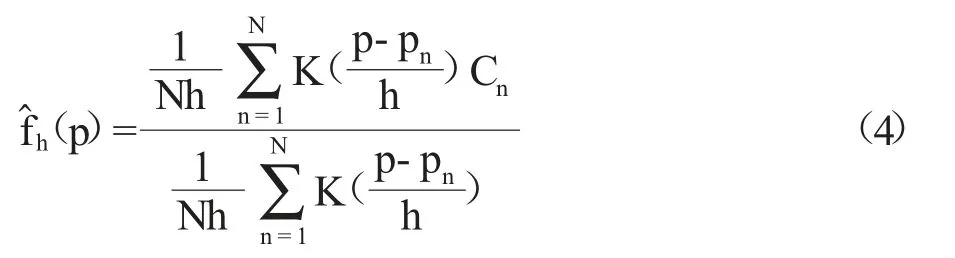
其中,p 表示解释变量;pn表示真实观测到的价格点;N 表示价格点的数量;Cn表示价格点pn所对应的BootStrap 置信度的估计;K(·)表示已知核函数,本文选取应用较广的高斯核函数作为本文的核函数;h 表示根据数据所估计出的窗宽,窗宽h 可以看作是处理偏方差权衡的平滑参数。如果窗宽太小,可能导致数据的过拟合。反之,如果窗宽太大,可能会导致估计过度平均化,偏差和残差较大,因此窗宽h 的选取尤为重要。本文的最优窗宽选取渐进积分均方误差方法获得。
四、实证分析
为验证上述数据稀疏性处理方法的有效性,本文将分别对模拟生成的稀疏数据和真实的稀疏数据进行稀疏性处理和分析。
(一)稀疏数据生成方法
1.稀疏数据模拟步骤
在对数据进行稀疏性处理前,首先根据易逝品在线销售数据的特点,模拟生成稀疏数据,具体步骤如下:
①假设商家在线销售某种易逝商品,其定价区间为[a,b),在[a,b)范围内采样N 个不同的数值,记为p1,p2,…,pN,其中p1<p2<…<pN,这N 个数值分别代表该易逝品的N 个销售价格。
②假设该商品的销售价格pn保持不变的时长Hn在(0,m)范围内变动,在(0,m)范围内随机采样N 个不同的整数,记为H1,H2,…,HN,这N 个整数分别代表N 个销售价格各自保持不变的天数。
③假设每个销售价格pn(n=1,…,N)对应的日销售量υn服从参数为λn的泊松分布,即υn~P(λn)。参考Gallego 和Ryzin[13]的研究中关于需求的假设:需求随着价格的升高逐渐降低,即当p1<p2<…<pN时,有λ1>λ2>…>λN。假设每个销售价格pn对应的日销售量均值λn在范围(c,d)内变动,先在范围(c,d)内采样N 个不同的数值,记为λ1,λ2,…,λN,其中λ1>λ2>…>λN,然后根据N 个泊松分布υ1~P (λ1),υ2~P (λ2),…,υN~P(λN),分别模拟生成N 组数据,每组数据表示每个销售价格在其价格保持不变的时长内的若干个日销售量值。在模拟过程中,要保证这N 组数据中各组数据的数据量与H1,H2,…,HN的值对应相等。
④将步骤③中模拟生成的N 组销售量分别与N个销售价格对应相乘,得到N 组销售收入数据,每组收入数据表示每个销售价格在其保持不变的时长内的若干个日销售收入值。
2.参数设置
为更好模拟出具有易逝品在线销售数据特点的稀疏数据集,本文将基于前文选取的真实数据集中各变量的数值,对上述模拟步骤中的各参数进行合理设置。由前文可知,在真实数据集中,销售价格在11.80—49.90 元之间变动,销售价格的总数量为50 个,销售价格保持不变的时长Hn在9—204 天之间变动,日销售量的均值大约为197 件。现参考真实数据集中的数值,对即将生成的模拟数据集中的参数进行设置,其设置原则为:与真实数据集有一定差异,但不能完全脱离实际。由于数据模拟过程中可能会受到随机因素的干扰导致达不到较为理想的效果,为增加数据稀疏性处理结果的可信度,本文将通过不同的参数设置及价格采样方式生成两个有一定差异的模拟数据集,使第一个模拟数据集(模拟数据集1)具有第二类稀疏数据的特点,即销售价格如何影响平均销售收入的有效数据点较少,而第二个模拟数据集(模拟数据集2)具有第三类稀疏数据的特点,即价格数据点是稀疏分布的。
假设商家在线销售的某种易逝品的定价区间为[50,100),商家将各售价保持不变的时长Hn控制在(0,100)范围内,故设置a=50,b=100,m=100。对模拟数据集1,借鉴王芷阳[14]在研究中使用的数据采样方式,在[50,100)上均匀采样30 个不同的数值pi(i=1,2,…,30),并假设模拟数据集1 中日销售量均值λn在(100,200)内变动,故参数设置为:N=30,c=100,d=200。对模拟数据集2,借鉴周启堃[15]在模拟稀疏分布的数据时的采样方法,在[50,100)上抽取50 个不同的数值pi(i=1,2,…,50),其中区间(50,60)、(60,70)、(80,90)和(90,100)各有5 个样本数据,而区间(70,80)内有30 个样本数据,并假设模拟数据集2 中日销售量均值λn在(150,250)范围内变动,故参数设置为:N=50,c=150,d=250。
3.稀疏数据生成效果展示及分析
为检验使用上述方法生成的两个模拟数据集是否具有各自不同的稀疏性特点,下面对模拟数据集1和模拟数据集2 的生成效果进行展示与分析。
图3是模拟数据集1 中各销售价格保持不变的时长Hn的分布直方图,Hn的均值为51.9 天。从图3可以看出,各价格保持不变的时长Hn的取值分布在0—100 天内,大部分价格保持不变的时长均超过一个月。由此可见,模拟数据较好地模拟出了易逝品售价长时间保持不变的特点。
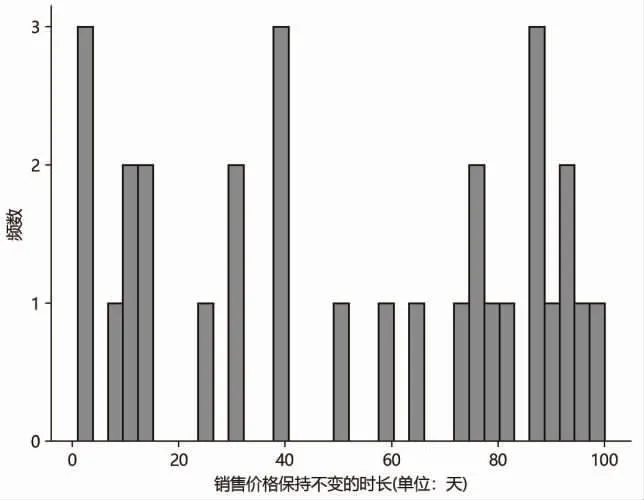
图3 销售价格保持不变的时长的分布直方图(模拟数据集1 )
图4是根据模拟数据集1 中各销售价格及其对应的平均销售收入绘制的散点图,这里的平均销售收入指某销售价格在其保持不变的时长内的日销售收入平均值。图中水平虚线代表所有销售价格对应的平均销售收入的均值。从图4可以明显看出,绝大部分的点较为均匀地分布在虚线上下400 元范围内,平均销售收入的波动范围较小,且数据点整体没有明显上升或下降的趋势,只有个别数据点对应的平均销售收入波动较大,无法得出销售价格与平均销售收入之间的关系,表现销售价格如何影响销售收入的有效数据点很少。由此可见,模拟数据集1 较好地模拟出了第二类稀疏数据的特点。
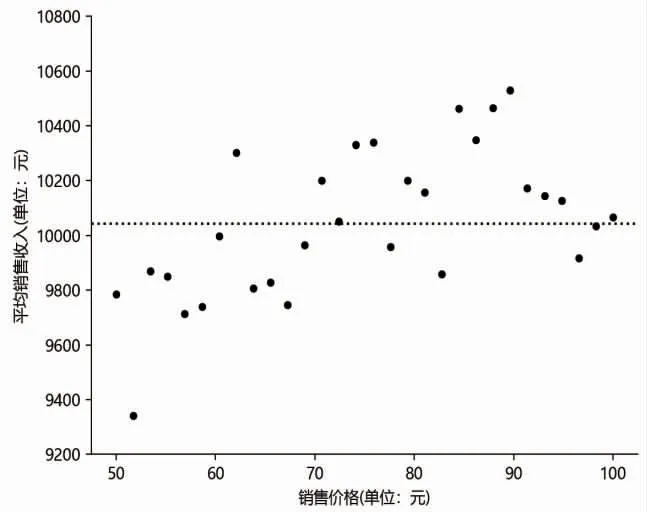
图4 销售价格-平均销售收入散点图(模拟数据集1 )
图5是根据数据集2 中各销售价格及其对应的平均销售收入绘制的散点图,这里的平均销售收入指某销售价格在其保持不变的时长内的日销售收入平均值。图中水平虚线代表所有销售价格对应的平均销售收入的均值。从图5可以明显看出,销售价格区间(50,60)、(60,70)、(80,90)和(90,100)内各有5 个数据点,而(70,80)内有30 个数据点,数据点分布严重不均。销售价格区间(70,80)内的数据点明显较密集,而其他区间内的数据点非常稀疏,数据点分布差距大,价格数据是稀疏分布的。由此可见,模拟数据集2较好地模拟出了第三类稀疏数据的特点。

图5 销售价格-平均销售收入散点图(模拟数据集2 )
(二)数据稀疏性处理及分析
本文将运用前文所述的数据稀疏性处理方法对模拟数据集1、模拟数据集2 以及真实销售数据集进行处理和分析,其中BootStrap 抽样次数W 设置为W=1000。
1.模拟数据集的稀疏性处理结果
图6是对模拟数据集1 进行稀疏性处理后的结果,其中,核回归的窗宽是根据渐进积分均方误差方法计算得到的最优窗宽,即h=8.57。从图6可以看出,经过稀疏性处理后,销售价格与其对应的BootStrap 置信度之间呈现出非线性关系,随着销售价格水平的升高,其对应的BootStrap 置信度先增大后减小。

图6 销售价格-BootStrap 置信度拟合图(模拟数据集1 )
图7是对模拟数据集2 进行稀疏性处理的结果,其窗宽是根据渐进积分均方误差方法计算得到的最优窗宽,即h=2.52。从图7可以看出,经过稀疏性处理后,销售价格与其对应的BootStrap 置信度之间呈现出非线性关系。当销售价格大约处于58—68 元之间和80—90 元之间时,随着销售价格水平的升高,其对应的BootStrap 置信度逐渐增大;当销售价格大约处于68—80 元之间、90—100 元之间时,随着销售价格水平的升高,其对应的BootStrap 置信度逐渐减小。

图7 销售价格-BootStrap 置信度拟合图(模拟数据集2 )
2.真实销售数据集的稀疏性处理结果
图8是对前文描述的真实销售数据集进行稀疏性处理后得到的结果,其核回归函数的窗宽是根据渐进积分均方误差方法获得的最优窗宽,即h=5.15。从图8可以看出,随着价格水平的升高,其对应的BootStrap置信度先逐渐增大后逐渐减小,通过核回归曲线可以清晰地看到价格水平与其对应的BootStrap 置信度之间的非线性关系。

图8 销售价格-BootStrap 置信度拟合图(真实数据集)
随着价格水平的升高,其对应的BootStrap 置信度先增大后减小的原因可能为:大部分消费者所能接受的最高售价大约为23 元,当商品的售价超出23 元时,消费者通常不会购买商品,导致商品在售价达到23 元以后,销售量急剧下降,销售收入随之下降。BootStrap置信度是基于对销售收入观测值反复抽样作出的估计,故BootStrap 置信度随价格水平变化的规律与销售收入随价格水平变化的规律具有一定的相似性。
五、结论
实际销售过程中,商家的销售收入是实时产生和变化的,因此具有较大的不确定性。本文对易逝品销售数据的稀疏性处理中,运用BootStrap 方法估计每个价格点对应的BootStrap 置信度,相当于利用概率思维量化了这种不确定性,之后又运用Nadaraya-Watson核回归拟合各离散价格点对应的BootStrap 置信度,Nadaraya-Watson 核回归不仅能够平滑相邻点之间较大的波动。增加结果的可靠性,还将真实数据集中没有但又处于定价区间内的价格点的BootStrap 置信度都作出了估计,不遗漏定价区间内的任何一个价格。通过核回归拟合结果不仅可以清晰地看到价格水平与其对应的BootStrap 置信度之间的非线性函数关系,还可以看出整个定价区间中价格的优劣,从而为商家制定定价策略提供一定的决策依据,也为后续的定价研究奠定了基础。◆

