地震作用下复杂土质边坡动力响应分析

张学辉 宁宝盛 彭雄志 苏平玉

1. 中铁建大桥工程局集团第五工程有限公司 四川 成都 610031 2. 西南交通大学土木工程学院 四川 成都 610031

我国西南地区位于印度洋板块与亚欧板块之间，地震断裂带十分活跃，是我国的一个地震高发区[1,2]。而在该地区一大批高速公路、铁路建成通车，强震作用下边坡的动力响应和稳定性一直是工程界普遍关心的问题。然而地震作用下边坡破坏机理复杂，如何正确认识边坡的动力响应及破坏模式还在不断探索中。Kutter[3]通过离心机边坡模型试验研究边坡的动力响应特征，认为塑性变形会使坡体的阻尼增大，边坡表现非线性特征，边坡屈服加速度会造成应变软化效应。刘春玲[4]等讨论了利用 FLAC3D进行边坡动力分析时如何设置边界条件、合成、输入以及转化动力时程。唐洪祥[5]等基于地震动力时程反应和随机地震反应，用有限元边坡稳定性分析方法，指出地震动力作用下土石坝边坡与正弦波作用下模型坝边坡的最危险滑动面位置有所不同。于玉贞[6]等以ELcentro波为动激励，对均质砂土边坡进行动力离心机模型试验。刘汉香[7,8]等研究了模型在天然波和正弦波作用下水平向和竖向加速度响应的变化规律。

本文以西南地区某特大桥右岸边坡为背景。该工程项目区内地形地貌较复杂，岩土种类较多，性质变化较大，基岩面起伏变化较大，不良地质作用较发育。工程场地50年超越概率2%的水平地震动加速度峰值为0.315g，相应地震基本烈度为VIII度。所以边坡稳定性问题是一个重点关注的对象。研究中考虑了边坡岩土体材料的动力特性以及地震动特性，采用动力有限元时程分析方法对边坡在地震荷载作用下的动力特性进行分析，并选取不同深度不同横纵向内部及临坡面测点进行动力响应特征分析，以揭示边坡动位移、动速度、动加速度和速度、加速度放大系数的响应特征规律。

1 动力响应时程分析法

动态时程分析法最初是通过计算机提取多次地震波数据，然后直接将记录的地震波用于下次的地震动分析中。动态时程分析法同时考虑了多种因素对结构动力响应的影响，如材料性质、模型边界、阻尼作用等，通过有限元软件（本次研究中使用Midas/GTS）对边坡进行地震动力响应模拟。通过对地震作用下的微分方程进行逐项积分求解，记录不同部位各时刻点的加速度和位移响应，然后由该数据计算求解瞬时位移和内力响应。该分析方法可以较为准确的进行地震分析，且能清晰的反映出结构在地震作用下的作用机制以及破坏过程，为改进桥梁边坡的抗震性能设计方法提供了一定的理论基础。

2 工程实例

2.1 计算模型及边界条件

由于地震影响范围较广，为了保证计算不受边界条件的影响，应尽量将计算边界取的足够远，结合所依托工程右岸复杂土质边坡的地质条件，选取动力模型范围尺寸为“顺桥向×横桥向×高程方向：X×Y×Z=238×206×199（m）”进行三维建模。首先根据等高线地形图生成地形表面，此次借助Midas自带的插件TGM生成了地形表面图，再根据地勘层面资料，划分地层。

Midas中划分网格：以四面体为主，网格尺寸在3m左右。桩基附近的网格进行加密，最后一层地层网格单元尺寸由3m向5m过度。整个模型共包含787,821个单元，139,390个节点。建立后的模型如下图所示：y轴正方向为山嘴方向，x轴负方向为坡脚方向。

图1 三维有限元模型

为了避免地震波在边界上的反射，左侧边界、底部边界和右侧边界均设为自由场边界，本文的边坡模型的主体网格为非均匀状态，这时主体网格的运动和自由场网格的运动将不一致，边界上的自由场阻尼器将发挥作用，减少地震波在模型内的反射。水平向地震加速度施加在底部边界上，使之成为动态边界，底部边界和右侧边界的法向速度设为0。

2.1 计算参数及输入地震加速度

根据勘察成果，并参考相关手册[9]，确定本次研究所需岩土体材料的力学参数如表1。

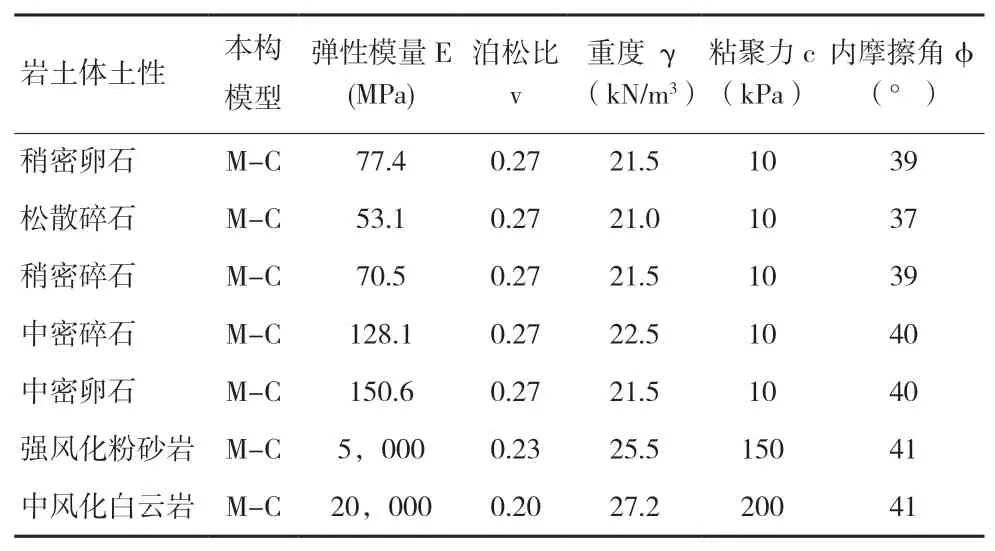
表1 岩层的计算参数

地震动输入选用实际地震动记录加速度时程。地震作用参数选用基准期设计加速度时程50年超越概率2%，阻尼比5%，相应水平的地震峰值加速度为0.315g，输入到图2所示的模型底部。根据地震反应谱生成加速度时间历程曲线，具体见图3，总历时为40s。

图2 边坡计算模型示意图

图3 输入地震动加速度时程曲线

3 复杂土质边坡动力响应结果分析

图4中展示了边坡中不同深度（Z）和不同横纵向（X和Y）内部及临坡面的测点位置。根据各测点的动位移、动速度和动加速度探究复杂土质边坡的动力响应。

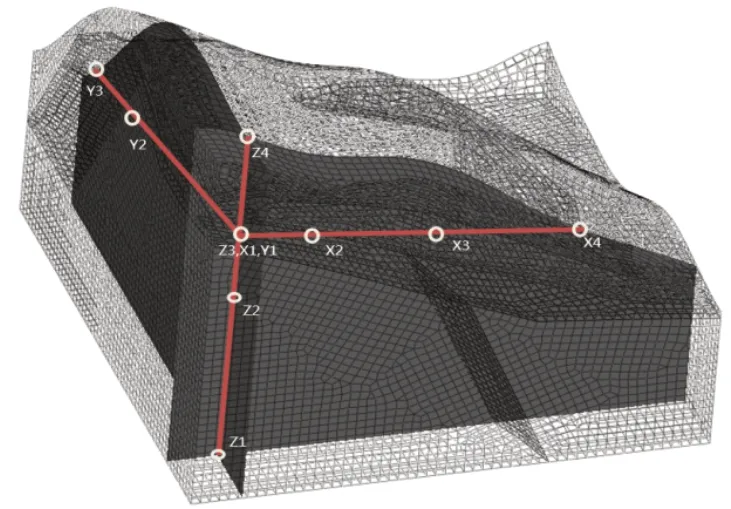
图4 边坡中X、Y、Z方向测点布置示意图

3.1 边坡三相动位移响应规律

图5所示为沿高程分布质点Z1、Z2、Z3、Z4三相（T1、T2和T3）分位移及总位移动力响应历程曲线。从图中可看出，不同高度分布的测点在动力响应上展现出波的一致性，都是呈现多幅值的振荡脉冲图形，最大峰值都出现在8-9s之间，这与输入的地震动信号几乎一致，不存在明显的滞后超前现象。

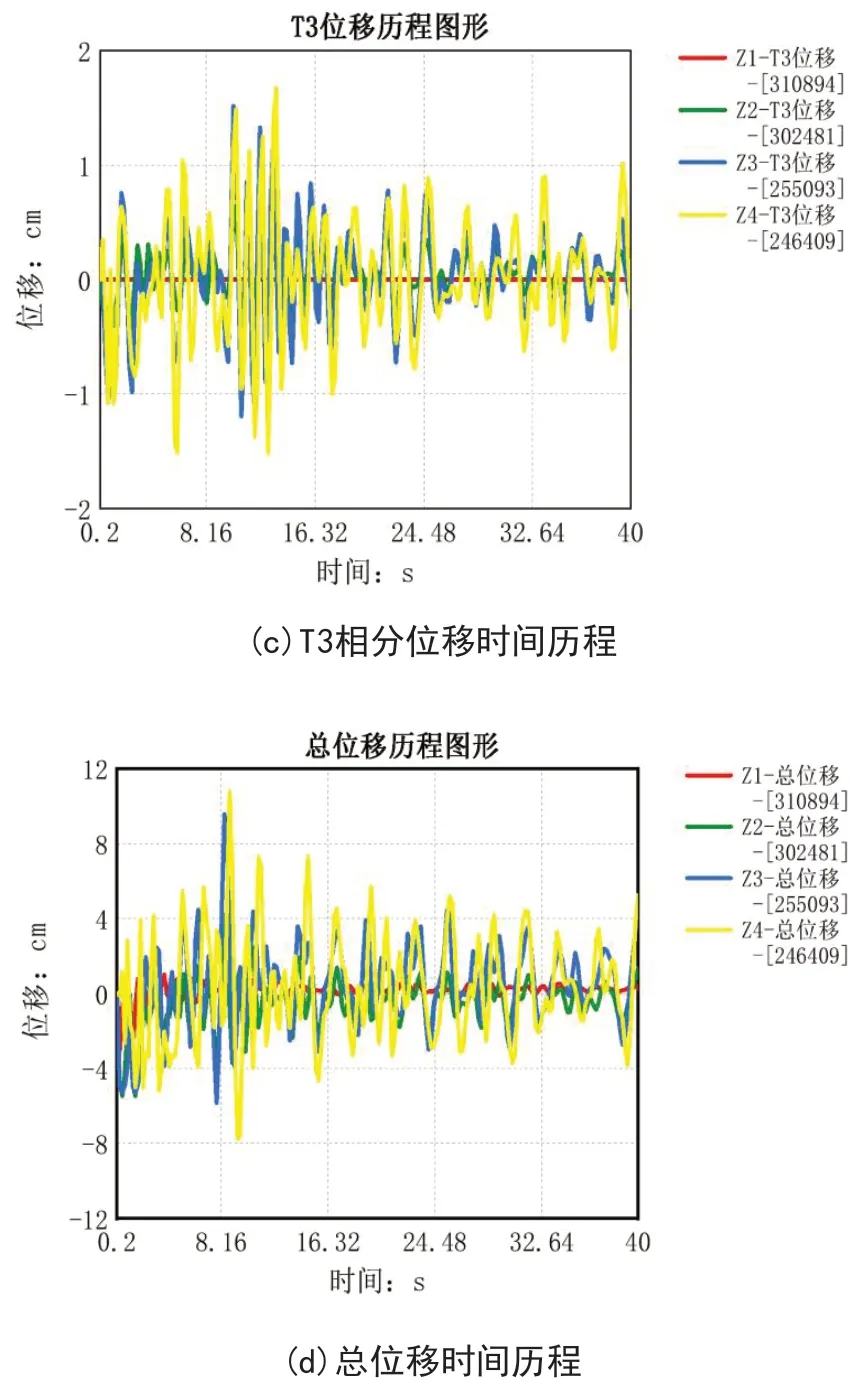
图5 沿高度分布测点位移响应时程曲线([]数字表示单元节点编号)

在对比三相分位移与总位移时可以看到，测点的位移标量大小主要由T2向分位移所主导，这与边坡坡向角度Y坡角（横桥向）明显大于X向（顺桥向）相关，说明地震作用下质点动位移与坡向角度有密切关联。沿高度分布测点Z1-Z4，无论分位移与总位移都呈现随着高度的增加在铅直方向上增大的现象，同时伴随测点高程的增加其动位移幅值也逐渐增大，这印证了祁生文[10]边坡动力响应规律研究中边坡动力响应的位移在铅直方向会出现放大作用，边坡边缘部位对振动的反应幅值较之内部存在放大现象的结论。经计算分析，沿X和Y方向分布的质点也存在上述的现象。

图6 沿XYZ分布测点位移放大比

图6所示为沿X、Y、Z方向分布测点最大位移的放大系数（PGD），同高程不同X、Y分布质点虽在三相分位移上放大比增长现象略有不同，但总位移放大比都是先小幅减小然后增大，且增大比例几乎一致，这说明总位移放大比与在同一高程处具有相似的放大规律，而分位移的放大比在同一高度从内部到临空面，质点动位移相比于其他两个分位移方向，对T3方向（高程方向）的分位移放大现象最为敏感，这说明地震作用下土质边坡的质点粒子振动方向受垂直于波的前进方向的影响更大。但无论沿X，沿Y还是沿Z分布质点动位移都存在从内部到临空面放大比增大的现象。

3.2 边坡三相动速度响应规律

图7所示为沿高程分布质点Z1、Z2、Z3、Z4三相分速度及总速度动力响应历程图形，各分布测点在动力响应具有统一的波形形式，T2相最大峰值出现在8s前，略前于输入的地震动信号峰值，这是由于坡面的坡向角度在Y方向（横桥向）大于X向（顺桥向），说明质点的速度传递与边坡的角度存在密切联系，且坡向角度越大的方向越早出现速度峰值；T1相、T3相最大峰值出现在8S后，略滞后于输入的地震动信号峰值。

图7 沿高度分布测点速度响应时程曲线

在对比三相分位移与总位移时可以看到，测点的速度标量大小主要由T2向速度所主导，这也与土质坡的坡向角度有关，说明地震作用下沿高程分布质点动速度的大小与坡向角度有密切关联[11]，坡向角度越大则该相分速度峰值越大。在沿高度分布测点Z1-Z4，无论分速度还是总速度都呈现随着高度的增加在铅直方向上增大的现象，这与李鹏[12]等通过建立边坡动力分析模型并对典型剖面进行动力响应特征分析得出，当高程增大时，动速度也会增大并且靠近坡面量值更大的结论一致。计算结果分析在沿X、Y方向分布的质点的速度三相结果也存在上述的现象。

图8 沿XYZ分布测点速度放大比

图8所示为沿X、Y、Z方向分布测点最大速度的放大系数（PGV），沿X分布测点总速度放大比最大达到2.5，沿Y分布测点总速度放大比最大达到1.8，沿Z分布测点总速度放大比最大达到2.2，说明无论沿高度方向还是横纵向方向，边坡质点速度主要呈现从内部向临空发展放大的现象。从各分速度放大比来看，沿X向分布质点对T1向（顺桥向）分速度放大变化最敏感，Y向分布质点对T2（横桥向）向分速度放大变化最敏感，Z向分布质点对T3（高程向）向分速度放大变化最敏感，这说明质点位置的变化对于速度的分相改变具有同倾向性，结合放大比来看这种同倾向性变化的规律并不一定是线性的。

3.3 边坡三相动加速度响应规律

图9所示为沿高程分布质点Z1、Z2、Z3、Z4三相分加速度及总加速度动力响应历程图形，可以看出沿着高程增加方向，三相分加速度和总加速度均呈现增大的趋势，各分布测点在动力加速度响应具有统一的波形形式。分相加速度和总加速度峰值出现的时间大致都在9s后，且随着质点高程的增加峰值出现的时间顺延发生，但都略晚于输入的地震动信号峰值时间。同时从图9(d)可以看到，Z1、Z2、Z3、Z4峰值加速度出现的时间依次存在后延现象，这说明随着质点高程的增加地震响应加速度峰值滞后现象越明显。

图9 沿高度分布测点加速度响应时程曲线

在对比三相分加速度与总加速度时可以看到，测点的加速度标量大小主要由T2向分加速度大小占主导，这可能与Y向坡的走向更大和坡角更大有关，但这种现象在临空面质点Z4（包括X/Y方向X4和Y3质点）表现最为明显：比如Z3质点T2相峰值加速度为T1相峰值加速度1.65，为T3相峰值加速度1.62倍，标量大小占总加速度的45%；而到Z4质点时T2相峰值加速度为T1相峰值加速度2.90倍，为T3相峰值加速度3.29倍，标量大小占总加速度的61%；而在沿X、Y方向的临空坡面质点X4其T2相分加速度标量占总加速度达到55%，质点Y3其T2相分加速度标量占总加速度达到65%，究其原因可能是临空面对地震波的反射叠加作用加剧临空面质点更有向坡向方向和坡角更大的方向振动的缘故。

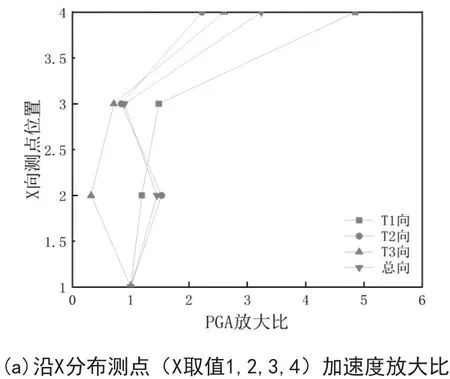
图10 沿XYZ分布测点加速度放大比

图10所示为沿X、Y、Z分布测点峰值加速度的放大系数（AFA），沿X、Y、Z分布测点总加速度放大比最大分别达到3.10，1.35，3.49；X4、Y3、Z4三个表面质点总相加速度峰值数值分别为4.72m/s2、5.08m/s2、3.82m/s2，相比于输入地震峰值加速度分别放大1.53、1.65、1.24倍。表明加速度放大系数随高度的增加逐渐增大，坡体内监测点放大系数小于相同高度的坡面监测点放大系数，临空面的放大效应显著。边坡质点加速度都呈现从内部向临空发展放大的现象。

4 结论

本文基于动力响应时程分析法研究西南地区某特大桥右岸土质边坡的动力响应特征，对地震作用下的坡体不同监测点处的质点位移响应、速度响应、加速度响应的分相及总相进行分析。结果表明：

（1）坡体沿横纵及高程方向对输入地震动均有不同程度的放大的作用，而且输出加速度峰值出现时刻较之输入地震有滞后现象，且这种滞后现象随着质点高程的增加愈加明显，而同高程处不同横纵位置质点在由向坡体内部到临空面这种滞后现象不明显，但都滞后于输入加速度峰值时刻。文中选取的临空坡面观测点X4、Y3、Z4相比于输入地震峰值加速度分别放大1.53、1.65、1.24倍；分相加速度存在某相标量大小不均匀偏大的现象，这种偏大现象在临空面质点上表现更为明显，整体呈现临空面位置质点坡角越大的方向则该相分相加速度占比越大。

（2）坡体内部对响应的地震动PGV存在垂直和临空面增大现象。垂直放大作用即是PGV放大系数随着高度的增加而变大；临空面放大作用，即是坡体同一高度上坡面响应地震动速度增大现象要大于坡体内部。从分相速度上来看，不同位置质点分相速度的放大变化存在伴随质点位置改变的敏感性和同倾向性，而这种敏感性和同倾向性并不一定是线性的。

（3）坡体质点在地震动输入下，其动位移响应时程变化展现为统一的波的形式，整体表现为多振荡的脉冲图形。同时无论分位移还是总位移，沿XYZ分布的质点都展现出明显的从坡体内部到临空面的位移放大现象。