局部冰塞体尺寸对桥墩绕流和冲刷的影响

刘 昂，田 璐，陈启刚，王忠祥，徐杰梁

(1.中交基础设施养护集团有限公司，北京 100011； 2.北京交通大学 土木建筑工程学院，北京 100044)

0 引言

水毁是造成桥梁垮塌的主要原因之一，其形式主要表现为桥墩或桥台基础的冲刷[1-2]。在高纬度地区，冬季河流结冰现象使桥墩基础的冲刷机理变得更加复杂，因此，研究河面结冰条件下桥墩绕流特征及基础局部冲刷机理对于我国北方地区的桥梁工程建设具有重要意义。

在桥梁冰毁事故高发的流凌期，冰块容易以局部冰塞体的形式在墩前堆积，对桥位河段水流特性及墩周河床冲刷产生影响。Wu等[3]分别对有无冰盖条件下半圆柱形桥台的冲刷规律进行了试验研究，阐述了半圆柱形桥台最大冲刷深度的所在位置。潘佳佳等[4]采用二维水冰沙耦合数学模型进行研究后发现，河道中即使没有桥墩存在时，冰塞体的形成也会导致河床冲刷量增大。Nyantekyi-kwakye等[5]采用PIV对冰塞体条件下的紊流进行研究后发现，河床和冰塞体的粗糙度越大，河床的冲刷程度越深。王军等[6]发现在流速和水深相同时，桥墩上游形成冰塞体后墩周局部冲刷深度明显大于明渠流和冰盖流，冲刷深度增加了约200%左右。除此之外，王军等[7]还通过水槽试验总结出了冰塞体存在时无量纲最大冲刷深度及长度与弗劳德数的关系式。Miranda[8]通过试验研究了桥墩上游冰塞体堆积长度对桥墩冲刷深度的影响，发现当冰塞体长度与冰下水深之比为13.2时，桥墩的局部冲刷深度最大，这与美国规范[9]中指出的堆积物长度与水深相等时墩周局部冲刷深度最大的结论存在较大的差异。对于墩前有堆积物的情况，美国规范中还提出了“等效墩径”计算公式，将公式计算得出的“等效墩径”代入到局部冲刷深度计算公式中，即可求得墩前堆积物和桥墩共同作用下的局部冲刷深度[9]。该公式是在枯枝、落叶等在墩前堆积的基础上研究得出的，是否可应用于墩前局部冰塞体堆积的情况还有待进一步考证。与此同时，我国公路及铁路工程水文勘测设计规范中还没有局部冰塞体条件下墩周冲刷计算的相关规定[10-11]。由此可见，目前对局部冰塞体影响下桥墩周围水流特性的研究较少，对局部冰塞体作用下桥墩周围局部冲刷机理的认识尚浅。

实际河道中，一定水流条件下墩前冰塞体尺寸会以水力或机械形式不断变厚加长[12-13]。本研究应用明渠水槽物理模型试验和三维水动力学数值模拟方法，研究平床条件下圆柱墩前形成局部冰塞体的墩柱绕流，分析冰塞体存在及其尺寸改变对墩周水流结构及床面切应力的影响，探讨冰塞体对墩周初始冲刷的影响及机理。

1 数学模型及计算工况

1.1 基本方程

基于Ansys-Fluent平台开展了局部冰塞体条件下的墩柱绕流三维数值模拟。采用雷诺平均法进行紊流模拟，对不可压缩流体的Navier-Stokes方程组进行平均处理，可得到雷诺平均Navier-Stokes方程组，其中连续性方程为[14]：

(1)

式中，xi为i方向上的坐标;Ui为i方向上的时均流速。

运动方程为：

(2)

为了封闭雷诺平均Navier-Stokes方程组，需要对雷诺应力项建立模型。本研究采用在圆柱绕流模拟中具有较好精度的k-ω模型，标准k-ω模型的湍动能k及其比耗散率ω输运方程为[15]：

(3)

(4)

式中，Γk和Γω为k和ω的扩散率；Yk和Yω为由扩散而产生的湍流；Gk为由平均速度梯度产生的湍动能；Gω为由ω产生的湍动能；Sk和Sω为源项;ui为i方向上的脉动速度。为了真实反映水流从明渠流到局部有压流的变化，模型中采用VOF方法进行水气交界的自由液面捕捉。

1.2 模型设置

模型采用三维矩形计算域，长、宽、高分别为50D，10D，2.5D，其中圆柱墩直径D=0.04 m。墩垂直放置于计算域宽度方向的中部，底面圆心与入口、出口、侧面之间的距离分别为12.5D，37.5D，5D。实际工程中，桥墩上游局部冰塞体的形状及尺寸差异较大。美国规范[9]中指出，墩前有堆积物存在时，堆积物的平面形状可概化为矩形或三角形。为便于建模分析，本研究设定局部冰塞体的平面形状为矩形，受桥墩的阻挡作用，冰塞体宽度取为一倍墩径。计算域边界条件如图1所示，采用流速入口，为减少运算时间并保证计算准确性，先计算一段纵垂向二维无柱模型以保证明渠紊流充分发展，取充分发展段的流速剖面作为三维模型速度入口；出口为压力出口；两侧面为对称边界；底面、局部冰塞体表面及墩壁面均采用无滑移壁面边界；顶面为对称边界。水的密度取1 000 kg/m3，黏性系数为0.001 567 kg/(m·s)，河床糙率为0.013，底坡坡度为0.001。

图1 边界条件Fig.1 Boundary conditions

为便于网格的划分，将计算域切割为5块区域。在圆柱附近采用非均匀结构化六面体网格，远离圆柱区域采用均匀结构化六面体网格，并在壁面附近对网格进行局部加密，网格划分示意图如图2所示。经过试算，最终确定壁面第1层网格高度为2 mm，网格总数量因冰塞体尺寸的不同在30～50万之间变化。

图2 网格划分示意图Fig.2 Schematic diagrams of gridding

1.3 模拟及试验工况

共设置18组工况对不同冰塞体尺寸条件下的圆柱绕流进行研究,计算工况如表1所示。入口断面平均流速U0为0.31 m/s，水深H为6 cm；墩柱雷诺数ReD=U0D/ν=7 913，属于紊动绕流流态；相对水深H/D>1.4，属于窄墩工况，即水深对绕流结构及局部冲刷的影响可以忽略[16]。美国规范[9]中指出：墩前有漂浮物堆积时，当漂浮物长度为一倍水深时，桥墩周围产生的冲刷深度最大，本研究设置局部冰塞体长度L分别为0.83H和2H。为便于后续分析，定义局部冰塞体厚度T与明渠水深H之比为冰塞体对水流的压缩度C=T/H×100%。

表1 计算工况Tab.1 Calculation cases

1.4 基于试验的数学模型验证

采用将数值模拟结果与局部冰塞体物理模型试验结果进行对比的方法，对本研究所建立的数学模型进行验证。试验在北京交通大学长3 m、宽0.4 m、高0.25 m的自循环顺直明渠水槽中开展。桥墩与局部冰塞体模型采用机玻璃材质的圆柱和长方体，长方体经过切割后固定在圆柱前端，墩径D为4 cm，局部冰塞体厚度C为1.32 cm，长度L为3.32 cm。试验时水槽底坡S=0.001，通过调节入口流量和尾门开度，形成水深H为4 cm的均匀流后，将模型固定在水槽试验段。水流示踪粒子为粒径20 μm、密度1 030 kg/m3的均匀微珠，采用最大功率为13 W的连续激光器形成厚度1 mm的片光照亮墩前水槽中垂面，并利用分辨率为1 280×1 024像素的高速相机搭配焦距50 mm镜头以500 Hz的帧频采集了25 000张连续的粒子图像，图像分辨率为12像素/mm。粒子图像由课题组自主研发的JFMeter®粒子图像测速(PIV)软件采用尺寸为16×16像素的判读窗口进行计算，窗口重叠率为50%，使得流速矢量之间的间隔为8像素。

在物理模型试验与数值模拟工况C3的流场数据中，分别选取典型流向位置和水深处的纵向平均流速剖面进行对比，如图3所示。从图中可以看出，数值模拟结果与试验结果的流速分布吻合较好；在墩前x/D=-2处纵向时均流速剖面的对比中，实测与模拟得到的纵向时均流速在壁面附近沿垂向快速增大，并在y/H=0.4附近取得最大值，之后逐渐减小，并在局部冰塞体下缘对应的垂向位置处出现拐点；在墩前y/D=0.025高度，纵向时均流速沿来流方向从x/D=-2处开始逐渐增大并约在x/D=-1.2附近达到最大值，之后由于受到墩柱的阻碍,速度迅速减小。以上结果表明本研究建立的数值模型的计算结果可靠。

图3 数值模拟与试验结果对比Fig.3 Comparison of numerical simulation and test results

2 结果分析

2.1 墩前流速分布

图4为桥墩上游形成两种不同局部冰塞体长度时，墩前对称面y/D=0.025高度的行进流速随局部冰塞体厚度的变化规律，其中C=0%为明渠流工况。当局部冰塞体对水流的压缩度较小时(如小于33%)，墩前床面回流逐渐减弱；与此同时，局部冰塞体下方的正向流动逐步增强。当压缩度达到67%时，墩前回流已基本消失。随着压缩度进一度增大，局部冰塞体下方的速度极值点逐渐前移，当压缩度超过83%～87%后，局部冰塞体下方的流动开始逐渐减弱，并在局部冰塞体前方床面附近形成新的回流区。当冰塞体厚度一定时，不同冰塞体长度条件下的速度极值基本不变。

图4 墩前对称面y/D=0.025高度处行进流速Fig.4 Velocity at height of y/D=0.025 in pier-front symmetrical plane

2.2 墩前涡流特征

墩周涡的定量识别采用广泛使用的Q准则，该准则使用速度梯度张量的二阶不变量作为涡识别变量，其数学定义为[17]：

(5)

式中,x,y,z分别为笛卡尔坐标系下的3个坐标分量；u,v,w分别为x,y,z方向的速度分量。

Q值大小反映了局部流体旋转速率对应变速率的超越程度，数值越大，表明涡的强度越大。图5展示了墩周涡结构对应的Q值云图，为了清晰展示涡核特征，涡核边界的Q值设置为36 s-2。由图5可见，桥墩上游形成局部冰塞体后，会导致床面附近的马蹄涡尺寸减小；当水流从无压流过渡为有压流时，在局部冰塞体下表面会形成大尺寸的涡结构；当局部冰塞体底部增长至临近河床面时，该位置处的涡可能会对床面冲刷产生影响；无论有无冰塞体存在，墩后均形成较多尾流涡结构。

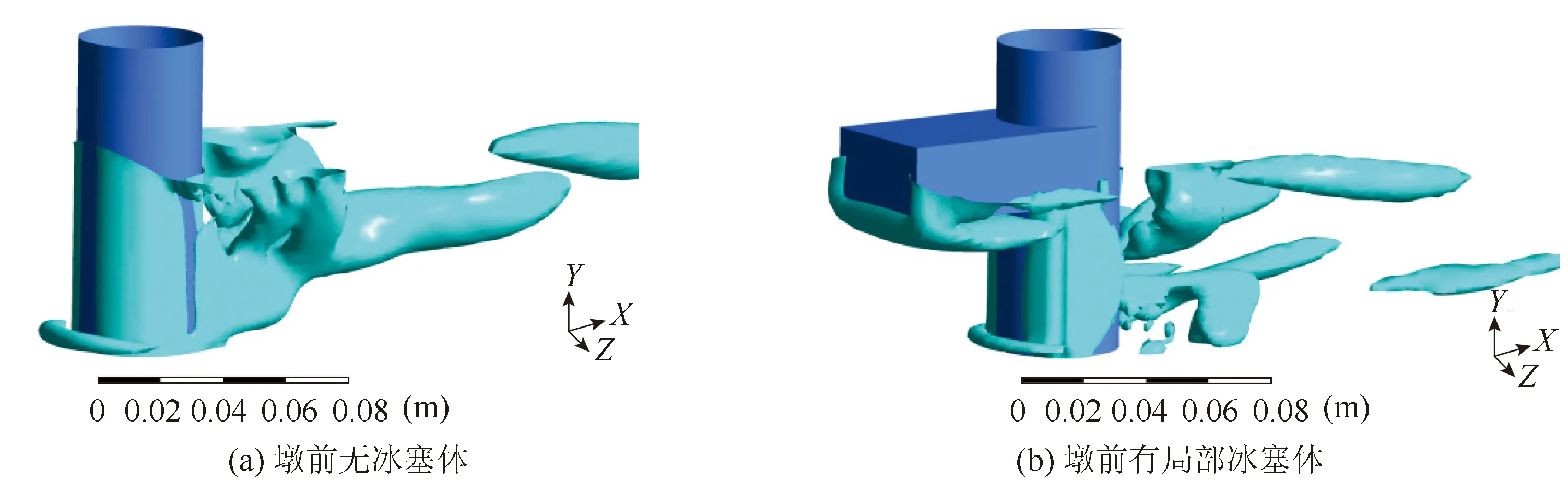
图5 Q值三维云图Fig.5 Three-dimensional nephograms of Q values

图6展示了L/H=0.83时不同局部冰塞体厚度条件下墩前对称面的Q值云图。由于L/H=2时呈现出相似的变化规律，故本研究未给出其Q值云图。由图6可见,在不同局部冰塞体厚度条件下墩前不同区域先后形成了4个主要的涡结构。为了便于分析，本研究根据这些涡结构对床面切应力的贡献特征，将其总结为3种类型：

图6 L/H=0.83时墩前对称面Q值云图Fig.6 Nephograms of Q values in pier-front symmetrical plane when L/H=0.83

(1)在明渠流条件下，墩前角落区仅存在马蹄涡结构(涡V1)，该涡在局部冰塞体对水流的压缩度超过50%后逐步消失。

(2)墩前形成局部冰塞体后，水流下潜进入局部冰塞体下方，主流与冰塞体底面之间形成分离区，分离区前端和末端角落区分别形成一个逆时针旋转的涡，将其统称为冰下回流涡V2。

(3)当局部冰塞体厚度较大时(压缩度超过50%)，局部冰塞体前方的一部分下潜水流受床面阻挡而沿河床向上游流动，在冰塞体上游形成类似马蹄涡的涡V3，当局部冰塞体对水流的压缩度为100%时，该涡发展成为完整的冰前马蹄涡。

图7进一步展示了局部冰塞体尺寸L/H=0.83及压缩度C=33%时通过PIV试验测得的墩前对称面Q值云图。可见图中出现了与对应工况数值模拟结果图6(c)相同的马蹄涡结构V1和冰下回流涡结构V2，且涡出现的位置与数值模拟结果吻合较好，试验与数值模拟得到的规律类似，进一步说明了数值模拟结果的可靠性。

图7 L/H=0.83时墩前对称面Q值云图(试验)Fig.7 Nephogram of Q value in pier-front symmetrical plane when L/H=0.83(by experiment)

为了更清楚地认识这3种涡的变化规律，分别提取了涡在不同局部冰塞体尺寸条件下的位置、大小和强度。根据Q准则的数学定义，Q值非0的区域均可定义为涡核。但在实际流体中，由于流体的连续性，总需要定义一定的阈值才可合理提取涡核区域。本研究在对涡结构进行定量分析时，对于所有工况均定义Q值大于3 s-2区域为涡核；涡的位置、强度分别以涡核中Q值最大值点的坐标和大小表示。

图8展示了不同局部冰塞体尺寸条件下3种涡在墩前对称面的径向位置。局部冰塞体下表面回流涡V2和墩前马蹄涡V1基本不受冰塞体厚度变化的影响，其中冰下回流涡V2的中心始终位于局部冰塞体前端，墩前马蹄涡V1的径向位置距墩中心距离大约为0.65D，与明渠圆柱绕流试验结果[18]基本一致，冰前马蹄涡V3整体随局部冰塞体厚度增大而向靠近桥墩的方向移动。

图8 涡在墩前对称面的径向位置随压缩度变化趋势Fig.8 Trend of radial position of vortex in pier-front symmetrical plane varying with compression degree

图9为3种涡在墩前对称面的垂向位置变化规律。墩前马蹄涡V1至床面的距离不随局部冰塞体尺寸变化而变化，始终保持在0.07D左右，与明渠圆柱绕流试验结果[18]一致。冰下回流涡V2的垂向位置基本不受局部冰塞体长度变化的影响，但会随局部冰塞体厚度增大而降低，其中心至床面的距离与局部冰塞体下水深始终保持一致。冰前马蹄涡V3自从出现后，随着局部冰塞体对水流的压缩程度增大，其中心不断向床面移动，最终稳定在约0.15D位置。上述垂向位置变化趋势表明，随着冰塞体厚度增大，涡V2及V3对床面的动力作用将逐步增强。

图9 涡在墩前对称面的垂向位置随压缩度变化趋势Fig.9 Trend of vertical position of vortex in pier-front symmetrical plane varying with compression degree

由于涡结构横截面类似于圆，将所有涡核面积换算为等效半径并绘制于图10。由图中可见墩前马蹄涡V1的等效半径r随局部冰塞体对水流压缩程度的增大而减小，且均明显小于明渠流，说明墩前局部冰塞体在压缩水流的同时，也会对马蹄涡形成一定程度的挤压；当局部冰塞体对水流的压缩度达到50%～67%时，墩前马蹄涡V1基本消失；局部冰塞体长度改变对墩前马蹄涡V1尺寸的影响较小。冰下回流涡V2在局部冰塞体压缩度小于50%时变化较小，这是因为此时该涡与床面之间的距离较远，其生存空间基本不受约束；当压缩度大于50%后，局部冰塞体下的水深相对较小，涡中心至床面的距离与该涡的等效半径逐渐接近，如图11所示，涡生存空间开始被压缩，等效半径随压缩度增大而减小。冰前马蹄涡V3面积随压缩度增大而呈增大-减小-增大的变化规律，但整体变幅不大。

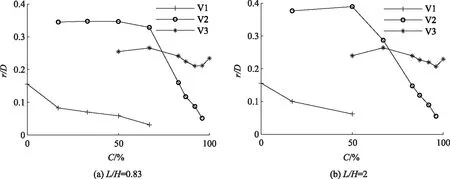
图10 涡等效半径随压缩度变化趋势Fig.10 Trend of vortex equivalent radius varying with compression degree

图11 涡垂向位置与等效半径之比随压缩度变化趋势Fig.11 Trend of ratio of vertical position of vortex to equivalent radius varying with compression degree

图12展示了墩前对称面各涡的强度随压缩度的变化趋势。随着局部冰塞体对水流的压缩程度增大，墩前马蹄涡V1的强度先增大后减小，并在C=67%时趋近于0。当局部冰塞体对水流的压缩度小于50%时，马蹄涡面积不断减小，根据亥姆霍兹涡管强度保持定理，涡截面的缩小将导致马蹄涡强度增大。当局部冰塞体对水流的压缩度大于50%后，主流对墩前马蹄涡V1的补给减弱，使其强度逐渐减弱直至消失。局部冰塞体长度改变对墩前马蹄涡V1强度的影响较小。

图12 涡最大Q值随压缩度变化趋势Fig.12 Trend of maximum vortex Q value varying with compression degree

图12中冰下回流涡V2的强度随压缩度增加先增大后减小。局部冰塞体对水流的压缩度小于67%时，随着局部冰塞体对墩前水流的挤压，冰下的最大流速逐渐增大，局部冰塞体下表面涡的强度不断增大。当局部冰塞体对水流的压缩度大于67%后，由于局部冰塞体下表面至河床的距离较短而限制了该涡范围的扩张，但随着局部冰塞体对水流的压缩度增大，局部冰塞体下水流流速依然较大，从而该阶段形成的涡强度急剧增大，对床面的扰动作用将极为显著。当局部冰塞体对水流的压缩度达到87%～92%后，局部冰塞体下水深已非常小，此时由无压流转变为有压流的水流流量减少，大部分水流从局部冰塞体边缘绕流而过，从而导致该涡的强度急剧减小。

图12中冰前马蹄涡V3在形成初期强度极弱，直至局部冰塞体对水流的压缩度超过92%时才随压缩度的增大而快速增长。局部冰塞体对水深的压缩度达到100%时，局部冰塞体前端形成完整的马蹄涡，强度达到最大。

2.3 床面切应力分布特征

随着水流结构的变化，墩周床面切应力分布也随着压缩度改变而发生变化。图13展示了L/H=0.83时不同局部冰塞体厚度条件下墩周床面切应力分布云图。为便于推广应用，各点床面切应力均以相同流量条件下明渠不受墩柱干扰位置的床面切应力τ0对墩周床面切应力进行无量纲处理。当墩前局部冰塞体对水流的压缩度小于50%时，墩周床面切应力的分布规律与明渠流类似：在墩前由于马蹄涡V1的作用而产生反向床面切应力极值区；在墩侧，由于桥墩压缩水流和马蹄涡的共同作用，在绕桥墩约±70°的方向上产生两个正向床面切应力极值区。与明渠流不同的是，局部冰塞体导致墩侧的正向床面切应力极值和墩前反向床面切应力极值减小，但上述极值点外侧的正向床面切应力整体增强。随着冰塞体厚度进一步增大，由于墩前马蹄涡V1强度逐渐减弱并消失，墩前反向床面切应力区域逐渐减小至消失；与此同时，由于冰下回流涡V2对主流挤压增强导致近床面水流流速增大，使得墩前逐渐形成一个正向床面切应力峰值区域，且该切应力的大小显著大于墩前马蹄涡V1诱导产生的反向切应力；当局部冰塞体对水流的压缩度达到92%后，进入局部冰塞体下部的水流已十分微弱，使得冰下床面切应力整体快速减弱；而在局部冰塞体前端，随着冰前马蹄涡V3强度增大，床面逐渐出现一个新的反向床面切应力区域。

图13 L/H=0.83时墩周无量纲床面切应力云图Fig.13 Nephograms of dimensionless bed surface shear stress around pier when L/H=0.83

为了定量分析床面切应力变化规律与墩前涡结构变换之间的关系，分别展示了如图14和图15所示的涡和墩前床面切应力极值的位置与强度随压缩度变化的趋势。由于涡强度与床面切应力的数值差异较大，分别以计算域内的最大值对涡强度和床面切应力进行无量纲化处理，使图15的纵轴变化范围保持在-1～1之间。根据图14可以发现，涡V1与墩前靠近桥墩位置处的反向床面切应力极值位置、涡V2与墩前正向床面切应力极值位置、涡V3与墩前远离桥墩位置处的反向床面切应力极值位置分别对应较好。与此同时，图15中涡V2强度与墩前正向床面切应力极值及涡V3强度与墩前远离桥墩位置处的反向床面切应力极值具有基本一致的变化规律，表明上述涡结构是导致墩前形成床面切应力峰值的主要机制。

图14 墩前涡与床面切应力极值径向位置关系Fig.14 Radial position relationship between pier-front vortex and extreme bed surface shear stress

图15 墩前涡与床面切应力极值强度关系Fig.15 Strength relationship between pier-front vortex and extreme bed surface shear stress

图16为不同冰塞体尺寸条件下墩周正向和反向床面切应力放大系数最大值的变化情况，图中τmax和τmin分别为墩周最大正向和反向床面切应力。不同局部冰塞体长度条件下墩周床面切应力峰值基本相等，但冰塞体厚度的改变会对墩周床面切应力产生较大的影响。当局部冰塞体对水流的压缩度小于67%时，墩周正向和反向床面切应力放大系数最大值均有轻微的减小，此时反向床面切应力最大值位于墩前和墩后。根据前述对涡的定量分析可知，当局部冰塞体对水流的压缩度达到50%时，冰下回流涡V2与床面距离较近，开始对床面产生扰动作用，但此时动力作用较弱，墩周正向床面切应力最大值依然位于墩侧。

图16 墩周床面切应力峰值Fig.16 Peak values of bed surface shear stress around pier

当墩前局部冰塞体对水流的压缩度在67%～92%范围内变化时，墩周正向床面切应力放大系数最大值急剧增大，并大于明渠流，反向床面切应力放大系数最大值基本保持不变。在该阶段反向床面切应力更多的是由桥墩尾涡引起的，最大值位置位于墩后；而墩周正向床面切应力最大值转移至墩前，冰下回流涡V2对该床面切应力起主导作用，由于涡V2强度急剧增大(见图12)，该位置处的床面切应力急剧增大，从而对床面产生不利影响。

当局部冰塞体对水流的压缩度大于92%且小于100%时，墩周反向床面切应力放大系数最大值增大，正向床面切应力放大系数最大值急剧减小。此时正向床面切应力最大值仍然是由涡V2引起的，位于墩前局部冰塞体的下方，该阶段局部冰塞体下表面与河床之间的距离很短，已经严重制约冰下回流涡V2的形成，从而导致该位置处的床面切应力减小。反向床面切应力最大值转移至局部冰塞体前端，这是由于此时冰前马蹄涡V3随局部冰塞体厚度增大而明显增强，并不断向河床靠近，使反向床面切应力增大。当局部冰塞体对水流的压缩度为100%时，局部冰塞体前端形成完整的马蹄涡，墩周反向床面切应力达到最大，由于此时桥墩迎流面由圆形变为矩形，所以切应力最大值大于明渠工况；冰塞体底部已无水流经过，正向床面切应力最大值转移至墩前冰塞体侧端位置。

以上分析表明，当墩前局部冰塞体对水流的压缩度为67%～100%时，由于冰下回流涡V2及冰前马蹄涡V3的接替作用，墩周床面切应力大于明渠流，表明局部冰塞体的存在对桥墩局部冲刷产生不利影响，主要表现为墩前冲刷坑的范围和深度增大，其中，局部冰塞体对水流的压缩度为92%时为最不利工况；反之，墩前局部冰塞体对水流的压缩度为0%～67%时，墩周床面切应力小于明渠流，墩前局部冰塞体的存在不会加剧桥墩局部冲刷。局部冰塞体长度改变对墩周床面切应力分布基本无影响。

3 结论

本研究以墩前局部冰塞体尺寸为变量，分析流凌期桥墩上游形成局部冰塞体后墩周流场及床面切应力的变化规律,得出主要结论如下：

(1)墩前形成局部冰塞体后，墩周因冰塞体厚度变化而先后出现墩前马蹄涡、冰下回流涡和冰前马蹄涡3种主要绕流结构，墩前和墩侧仍然是床面剪切力最大的区域。

(2)冰塞体厚度对水流压缩度小于50%时，随着冰塞体厚度的增加，墩前马蹄涡位置基本不变，尺寸逐步减小，强度逐步增大，墩前马蹄涡在下方床面诱导形成反向床面切应力极值，对床面起主要动力作用。

(3)当冰塞体厚度对水流压缩度超过50%后，随着冰塞体厚度的增加，墩前马蹄涡迅速衰减并消失，冰下回流涡的垂向高度降低，强度迅速增大；冰下回流涡在冰塞体前端下方诱导形成正向床面切应力极值，并在压缩度超过67%后成为对床面起主要动力作用的绕流结构。

(4)当冰塞体厚度对水流压缩度超过约90%后，冰下回流涡的强度迅速减弱，冰前马蹄涡垂向位置降低，强度增大，在冰塞体前方形成反向床面切应力极值，并在压缩度超过96%时成为对床面起主要动力作用的绕流结构。

(5)当冰塞体厚度对水流的压缩度超过67%时，墩周床面切应力大于相同条件下的明渠墩柱绕流，对桥墩局部冲刷产生不利影响，冰塞体长度对墩周绕流结构及局部冲刷基本无影响。