基于DMD-NARX模型的短期电力负荷预测方法

王雪菲， 李 勇， 余国晓， 程 晨， 杨辉军

(1.安徽国际商务职业学院 信息工程学院, 合肥 231131; 2.安徽财经大学 统计与应用数学学院, 蚌埠 233030;3.安徽大学 电子信息工程学院, 合肥 230601)

0 引 言

当今时代，电力系统安全、高效地运行是经济社会发展的基本支撑，而持续保障电力系统平稳有序运营的重要途径之一就是对电力负荷在不同时间跨度上进行针对性的有效预测[1]。根据预测的时间跨度，负荷预测被分为短期、中期和长期预测，而电力系统配件的检测维修、电网发电机组等设备的启动和关停以及不同地域之间的供需平衡是决定电网运行效益、降低成本和提高效率的关键，精确的短期预测对以上工作大有裨益[2]。

目前,常用的短期电力负荷预测方法主要分为时间序列方法和机器学习方法两大类[3]。其中时间序列方法包括多元线性回归法[4-5]、指数平滑模型法[6]和自回归积分移动平均模型法[7-8]等。这些方法考虑了负荷数据的时序性特点，根据历史负荷值来预测未来负荷值，建模简单，但反映负荷序列的非线性行为能力较弱，且在预测精度上关注度不够。机器学习方法主要包括模糊系统、神经网络和支持向量机(Support vector machine，SVM)等。文献[9]将支持向量机与计量经济学中的协整检验以及Granger因果检验结合起来预测经过季节分解的电力负荷。文献[10-11]使用BP神经网络(Back propagation，BP)对相应的负荷数据进行预测，文献[12-13]则针对短期用电负荷建立了人工神经网络模型进行处理预测。文献[14]以相关性数据作为电力负荷日预测的基础，通过相关性分析方法在模糊推理和灰色关联分析的基础上得出。机器学习方法能够较好地逼近非线性负荷曲线，但是缺少对负荷数据时序相关性的考虑，需要人为选择时间特征来保证预测的精度。为了充分评估负荷序列随时间波动的特性，含外部输入的NARX被逐渐运用在负荷预测领域[15-17]。NARX网络是一种有效用于时间序列预测的非线性动态循环神经网络，该网络当前时刻的输出不仅与当前时刻的输入有关，还与之前的输入输出有关，所以在数据非线性和时序性的处理上有所加强，但是在识别负荷序列潜在变化趋势上依然有所欠缺，无法充分提取出短期负荷数据之间蕴含的有效信息。

针对上述问题，提出一种基于DMD-NARX模型的短期电力负荷预测方法，有效提高了短期负荷预测精度。首先,运用ACF分析历史负荷数据获取相应日期内基于相应短期负荷波动时间规律特性的输入特征集合。其次，将该集合做归一化处理，然后运用Hankel把现有的单变量输入特征序列转换为多维数据矩阵，同时通过DMD模型将矩阵特征分解并取得动态模态估计。最后，将DMD方法得出的动态模态作为NARX神经网络的外部输入特征，并运用此模型推导出相应日期内各时段负荷的分布。

1 构建输入特征序列的Hankel矩阵

1.1 输入特征集合的确定

由于相邻时刻之间的负荷波动相对较小，同时短期内电力负荷的变化与时间存在内在联系，因此要分析出非连续负荷数据之间的潜在联系，本文须把目标时刻负荷作为参照，同时分析过去时刻负荷对目标负荷的影响[18]。同时，ACF标准的大量推广，就是为了能够选择出适宜的输入特征集合，并推导出负荷数据中的潜在联系[19]。假设一天的负荷序列表示为p=[pt:t∈T]，则t时刻与t-k时刻负荷间的自相关系数如式(1)所示：

(1)

在已有历史数据的基础上,结合ACF分析可以推导出3个最强相关性的滞后变量：上周同一日同时刻的值、t时刻前一时刻的值和前两日同时刻的值。基于以上分析，同时考虑到双休日的用电负荷普遍比工作日的用电负荷低，预测输入特征包括上周同一日的负荷数据、上周前一日的负荷数据以及前两日的负荷数据，因此本文取得的星期一、星期二和双休日输入特征集合需要分别表示[20]。星期一和星期二都是工作日，考虑到工作日之间的用电负荷相比较而言波动不大，所以其对应的输入特征集合分别由上周星期一到星期四的用电负荷、星期一和上周星期一到星期三的用电负荷构成；双休日两天的输入特征集合分别由星期五、上周星期五、上周星期六和上上周星期六的用电负荷和星期六、上周星期六、上周星期天和上上周星期天的用电负荷构成。不同预测日期的具体输入特征集合如表1所示，其中，Pset表示预测日期的输入特征集合，pD-d(d=1，2，4，5，6，7，8，14)表示预测日期之前d天所对应的日负荷。

表1 不同预测日期输入特征集合

1.2 构建Hankel矩阵

短期负荷序列是一组非线性时间信号，可由多个影响因素叠加组成，为了进一步提高短期负荷预测精度，需要精准获取负荷序列的动态特征，但是负荷序列的动态特征往往受到多种因素影响。通过将一维矩阵转为多维矩阵负荷序列转换的过程，有效提升后期DMD方法对电力负荷数据的变化趋势和底层多尺度动态的抓取能力，其中也包括对负荷数据矩阵进行特征分解和动态模态估计能力的提升。

首先，将预测日期输入特征集合Pset构建为输入特征序列Pis=[p1,p2,…,pk,…,pM]，并对Pis进行归一化处理，归一化形式为：

(2)

式中：xi为归一化后的输入特征；pmax和pmin分别表示序列Pis的最大和最小值。

(3)

2 短期负荷预测模型

2.1 动态模态分解(DMD)

DMD方法是围绕线性Koopman算子概念发展的数据驱动的矩阵分解技术[22]，通常应用于流体分析、复杂系统构建以及数据挖掘等方面。将空间维度上的主成分分析结合时间维度上的功率谱分析是DMD方法的创新点所在[23]，这种方法和只能提取一种模态的方法相比，由于可以在两者结合的基础上再提取出数据的时间和空间模态，DMD可以更加精确地感知到数据中存在的潜在趋势性。

假设X1和X2是由Hankel矩阵X创建的观察矩阵，数据按照Δt时间间隔开，并且随时间重叠。

X1=[x1,x2,…,xL-1]

(4)

X2=[x2,x3,…,xL]

(5)

在 Koopman 算子线性映射的运算策略基础上，一个与系统矩阵A实现相邻时刻状态的投影关联也可推导出，即xj+1=Axj，基于上述分析，式(4)和式(5)可进一步转换为：

X1=[x1,Ax1,…,AL-2x1]

(6)

X2=AX1

(7)

当前，观察矩阵X2的系统特性可通过矩阵A的属性，如特征值和特征向量等反映出来。需要指出的是，当动态系统变化逐渐变缓，线性依赖关系将在各个数据之间逐渐形成[24]，即X2中的观测值xL可以由前一时刻X1中L-1个观测值的加权线性组合表示：

xL=a1x1+a2x2+…+aL-1xL-1+r=X1a+r

(8)

式中：a1,a2,…,aL-1是L-1个观测值的权重；r是长度为S的残差向量。基于此，可推导出以下公式：

(9)

X2=AUΣVH=UΣVHB

(10)

B=VӆUHX2

(11)

(12)

式中：†是伪逆操作。对式(12)进行特征分解可得：

(13)

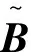
Ψ=UW

(14)

Ψ的每一列是对应于Λ中特征值λi的DMD模态。结合式(14)，Ψ推导出最终估计的模态如下：

(15)

式中：C=Ψ†x1表示DMD模态的初始幅度；Ω=ln(Λ)/Δt；t是一天中的时刻点。

2.2 NARX神经网络

NARX神经网络是一种动态循环网络，这种网络可以通过输入和反馈连接同时采用时间延迟的条件下获得，并且能够在下一次的迭代训练中在输入端使用输出信号，同时由于其本身的记忆体系较强，所以在对复杂映射关系的时变系统的描述上具备更强的能力，这也是该体系在非线性时间序列预测领域被广泛应用的原因[25]。与传统的循环神经网络(Recurrent neural network，RNN)综合比较，NARX在学习能力、收敛速度、泛化性能以及预测精度等方面表现出了更好的效果[26]。NARX的数学表达式为：

(16)

典型的NARX神经网络主要包括输入层、隐含层、输出层及输入和输出延时层几个部分，其基本结构如图1所示。图中，wih、who和wjh表示各层链接之间的权重；b0和bh均表示阈值；fh(·)和fo(·)分别是隐含层和输出层的功能函数；z-1表示一个步长的延迟。

图1 NARX神经网络结构图

NARX隐含层的作用是剔除不重要的信息，并在此基础上存储重要的信息。原则上隐含层层数与模型的非线性映射能力成正比，即层数越多，拟合效果越好。但是层数的增加也会导致训练时间的增长，所以一般会综合考虑，选择相对用时较少、性价比较高的方案。根据Kolmogorov定理，任意的非线性特性最多只需两层隐含层便可辨识出[27]，因此，模型只需选取一个隐含层即可，在此条件下既可以保障模型预测结果的匹配度，又可以节约大量的时间[28]。同时，按照以下的经验公式选取隐含层节点数，划定隐含层节点范围：

(17)

式中：h为隐含层节点个数；mi为输入层的节点个数；mo为输出层的节点个数。

2.3 建立短期负荷预测模型

基于DMD-NARX模型的短期电力负荷预测模型的主体结构由两块构成，DMD部分主要用于特征提取，NARX网络主要负责电力数据负荷的预测。负荷数据集因系统故障等原因，可能存在个别数据异常情况，异常数据往往和正常数值偏离较大，可采用模糊聚类[29]、神经网络和基于最大阈值法[30]等方法修正异常数据。模型流程图和模型整体程序伪代码分别如图2和表2所示。

图2 短期负荷预测模型流程图

表2 整体程序伪代码

(1)对以往的历史实际数据进行收集，并将数据进行一系列预处理，即对异常值进行修正，将其分为训练集和测试集；

(2)根据ACF分析结果，构建训练集和测试集的输入特征集合；

(3)先进行输入特征集合到输入特征序列的转换，并在成功完成归一化运算处理后将处理结果转换为多维特征Hankel矩阵，其滑窗的长度一般为一维特征序列总长度的四分之一；

(4)以Hankel矩阵为基础创建DMD的观察矩阵，然后通过DMD方法估计出负荷系统的动态模态；

(5)经过(4)的推导运算可得到NARX神经网络的外部输入特征，与动态模态对应时刻的历史负荷作为网络输出；

(6)在确定了延迟阶数和隐含层节点数之后，可以基于神经网络进行相应训练，在训练所得精度达到规定标准后可使用模型对测试集进行相应预测。

3 算例分析

3.1 算例数据

为验证本文所提方法的有效性和普适性，使用两个负荷数据集对模型进行验证，并将本文所提方法和NARX模型、传统RNN模型以及SVM模型方法的预测结果进行对比分析，为保证测试的严谨性，每种模型的输入输出特征以及预测时间点必须保持一致。两个负荷数据集分别是澳大利亚新南威尔士州公开数据集和中国安徽省合肥市的实际电力负荷数据集。新南威尔士州公开数据集提供了2006年1月1日至2010年12月31日共5年的电力负荷数据，每天取48个采样值，即采样频率是30分钟。合肥市的实际电力负荷数据集包括2016年1月1日至2017年12月31日共2年的电力负荷数据，每天取24个采样值，即采样频率是60分钟。

3.2 误差指标

本文选取的各种模型预测精度评价指标为平均绝对百分比误差(Mean absolute percentage error，MAPE)和均方根误差(Root mean square error，RMSE)。MAPE取值越小，模型的预测性能越好，其结果可以评价模型的优良性。而RMSE同样是取值越小越好，同时由于其对极大或极小误差的敏感度较高，其运算结果也可用以评价模型的预测精度。两个评价指标表达式为：

(18)

(19)

3.3 新南威尔士州数据集预测结果分析

由于电力需求数据的变化与不同季节气候的变化息息相关，因此若要充分验证模型识别气候和季节特征变化的能力，就必须通过对4个不同季节中负荷预测的结果进行分析，对比凸显本文所建模型的预测能力。对比测试中使用相同地区不同季节的前10周作为训练集(春季9月～11月、夏季12月～2月、秋季3月～5月、冬季6月～8月)，在此基础上同时对后一周电力负荷数据进行预测。图(3)所示是对相同地区不同季节中的某一天的预测结果进行对比。

根据图3观察得出，对比分析不同季节负荷数据的预测结果，与其对比方法相比，本文所提出的基于DMD-NARX模型方法，对原始负荷曲线具有更好的拟合能力，同时，由于电力负荷数据底层的变化趋势能够被DMD有效识别，因此，本文所建立的模型在负荷曲线波动较大的位置上亦可表现出更高的拟合度，从而验证了本文所提方法对提高短期负荷预测精度的有效性。

图3 不同季节日负荷预测结果对比

表3为不同方法对4个季节中某一天负荷预测的精度结果。由此可见，本文所提方法预测精度的平均值高于其他3种方法，其中eMAPE误差的平均值为0.57%，相比NARX模型、RNN模型和SVM模型方法精度分别提高了46.73%、60.14%和57.46%；eRMSE误差的平均值为66.38 MW，相比NARX模型、RNN模型和SVM模型方法，误差分别降低了69.52、92.09和82.34 MW。结合不同季节相应日期预测结果可以看出，NARX模型对时序预测的问题也取得了良好的效果，说明该模型对历史负荷信息的利用效率较高。下一步将DMD分解导入NARX神经网络模型中，通过这种方法在增强预测模型对负荷数据之间潜在关联和底层变化发掘能力的基础上，进一步增强了模型预测精度。

表3 不同季节预测日期负荷预测精度对比

表4为2007年2月17日部分时刻的负荷预测结果。从eMAPE误差的平均值可以看出，本文所提出的DMD-NARX模型和NARX对比模型各时刻点的eMAPE误差平均值为0.50%和1.42%，相比于SVM模型和RNN模型精度分别提高了75.73%和31.07%以及76.53%和33.33%。在NARX模型中，虽然个别时刻点预测精度接近99.95%，预测结果相对准确，但由于整体预测结果偏差较大，误差最大值达到9.82%，降低了模型整体的预测性能。而引入了DMD方法的NARX模型很好地解决了预测结果波动较大的问题，误差范围基本稳定在0.50%左右，既提高了负荷预测精度，又保证了预测结果稳定性。

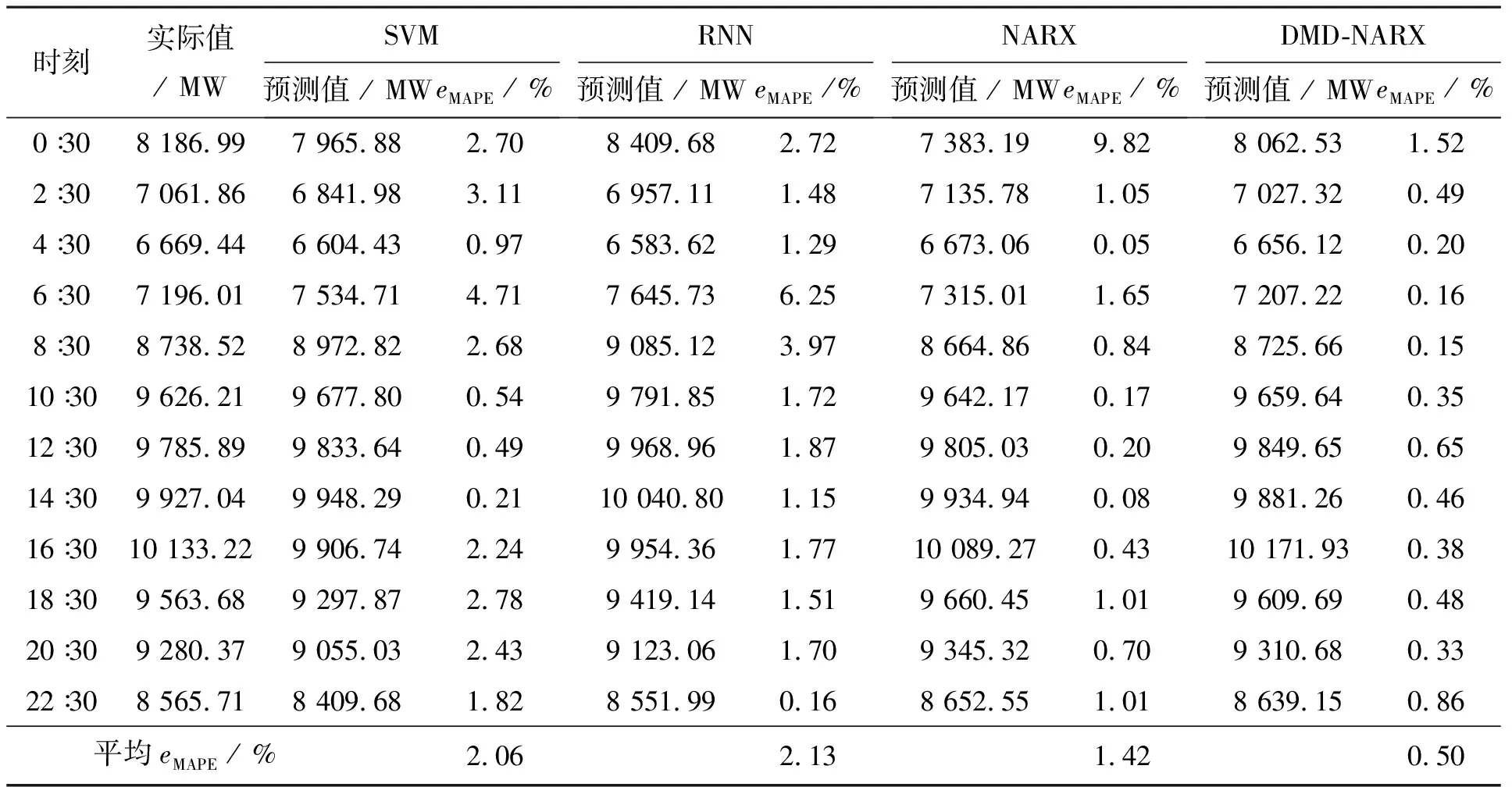
表4 2007年2月17日部分时刻负荷预测结果

3.4 合肥市数据集预测结果分析

将合肥市数据划分为两种数据集，神经网络常用训练集占总样本数据的2/3以上，为了保证预测模型的有效性，训练集是前10周的数据，测试集为后1周的数据，使用各类模型方法预测测试集的日负荷。图4为测试集在各类模型运行下的结果对比。

图4 各模型预测日期负荷结果对比

从几种不同方法预测结果的比较中可以看出，与原始负荷曲线拟合度相对较高的是DMD-NARX模型方法，即使在负荷变化较大的区域，DMD-NARX模型方法同样能进行较为准确的预测，且预测效果优于其它方法，这与对新南威尔士州负荷预测结果的分析是相同的，在负荷序列潜在变化趋势的抓取能力上，本文所使用的DMD方法具有一定优势，因此在电力负荷曲线出现较大范围波动时也表现出较高的拟合度。

表5为不同方法对2017年6月某周五的负荷预测精度对比。从表中可知，本文所提出的DMD-NARX模型方法的预测效果优于其他3种方法，eMAPE和eRMSE指标的精度分别是0.56%和98.78 MW，比其它3种方法精度平均提高了56.38%和59.93%，验证了所提模型对提高负荷预测精度的有效性及普适性。

表5 各模型预测日期负荷精度对比

4 结 论

提出一种基于DMD-NARX模型的短期电力负荷预测方法，得出以下结论：

(1)通过考虑负荷序列的时序变化规律和数据潜在的变化趋势，将DMD方法引入NARX模型中，既加大了对负荷序列潜在变化趋势的发掘深度，又提高了对负荷序列非线性变化的模型识别水平，同时针对负荷曲线波动较大的情况具备了更强的拟合能力，提升了预测模型的整体性能。

(2)与单一模型和其组合模型相比，本文所提出的DMD-NARX模型能够在预测精度高的同时保证模型的普适性能，符合负荷预测的实际需求。

(3)后续将结合注意力机制、残差网络等技术，充分挖掘更多可表征的预测特征，进一步提升预测精度。