基于改进FNN的降水粒子分类方法
李 海 郭生权 张超群 冯 青
(中国民航大学天津市智能信号与图像处理重点实验室 天津 300300)
0 引言
降水粒子分类对气象灾害性天气监测、强对流天气预报上具有重要的作用[1],与传统的气象雷达相比,双线偏振雷达可以发射水平和垂直电磁波从而获得与降水粒子类型、形状、尺寸、下落姿态等相关的差分反射率、相关系数等极化参数[2],能够更加准确地提供粒子的相态信息,因此双线偏振雷达广泛应用在层状云降水识别、中尺度对流、强对流风暴分析等方面[3]。
1994年Holler等人利用判决图来进行降水粒子分类[4],由于不同降水偏振量的边界模糊,所以该方法对降水粒子的分类不够精确,1996年Straka和Zrnic将模糊逻辑算法应用到降水粒子分类中[5],模糊逻辑是用规则推理而不是固定的公式来描述系统,在降水粒子分类中有明显的优势,Park等人在模糊逻辑算法引入融化层信息来去掉各高度层不存在的粒子,提升了相态识别的准确度[6]。在之后的研究中模糊逻辑算法被不断的完善[7-8],但是模糊逻辑方法过度依赖专家经验值,隶属度函数参数的设定具有较强的主观性,导致该算法灵活性差,会对分类结果造成一定的误差。随着机器学习技术发展,支持向量机[9],全连接神经网络[10]的方法被应用在降水粒子分类中,支持向量机在处理二分类上有较大的优势,但是在由二分类构建多分类降水粒子识别系统的过程中会成倍增加计算量;全连接神经网络能够依据数据调节降水粒子分类器参数,使分类结果更加可靠,但是该分类器对霰、冰雹等大颗粒固体粒子分类不敏感。Liu等人在2000年将模糊神经网应用降水粒子中[11],模糊神经网络既利用了模糊逻辑的特点又结合了神经网络自主学习的优势,解决了隶属度函数过度依赖专家经验值等问题,使分类结果更加可靠,但是隶属度函数参数初值的不易确定问题会影响模糊神经网络在训练过程中的稳定性,限制了该方法的识别效果。
为了解决模糊神经网络在训练过程中隶属度函数初值不易确定的降水粒子分类问题,本文提出了一种改进模糊神经网络的降水粒子分类方法。该方法利用无标签数据聚类结果和带标签数据(少量)之间的相关性分析来得到带标签数据,通过对带标签的数据进行统计分析来得到隶属度函数初值,接着使用训练集来对初值确定好的模糊神经网络进行离线训练,最后利用训练好的模型实现降水粒子的分类。该方法利用确定好的隶属度函数初值能够获得更加稳健的降水粒子分类器,并实现合理的降水粒子分类结果。
1 改进模糊神经网络的降水粒子分类方法
本文改进的地方体现在基于K-means++-MD的隶属度函数参数初值确定,利用数据统计分析来确定隶属度函数初值的改进模糊神经网络整体思路为:首先将无标签区域雷达极化参数的聚类结果和另一区域中少量带标签数据做相关性分析来得到带标签数据,接着对带标签数据进行统计分析来得到隶属度函数参数初值,之后将该初值代入模糊神经网络进行离线训练得到依据数据自适应学习好的降水粒子分类器。下面先描述模糊神经网络结构及离线学习过程,之后对K-means++聚类和马氏距离(Mahalanobis Distance,MD)联合算法得到的带标签数据进行统计分析来得到隶属度函数初值,最后用改进后的模糊神经网络来实现降水粒子分类。
1.1 模糊神经网络
模糊神经网络融合了模糊逻辑的特点和神经网络自主学习的优势,具有处理不确定信息的模糊推理功能和依据数据自主学习的能力,从而使神经网络系统中的权值具有模糊逻辑中推理参数的物理意义[12],在降水粒子分类中能依据数据学习自动调节隶属度函数参数,对降水粒子分类是非常有用的。
在模糊神经网络中,模糊逻辑部分可以搭建为一个多层前向传播神经网络,共有五层,即输入层(由输入变量组成)、IF层(模糊化层)、THEN层(规则推理层)、合成层、去模糊化层以及输出层。该模型在训练过程中利用神经网络学习算法可以用来获悉系统参数,其系统框图如图1所示,图中实线表示前馈路径,虚线表示误差的反向传播过程。分类的误差反馈到IF层来调节隶属函数的参数。
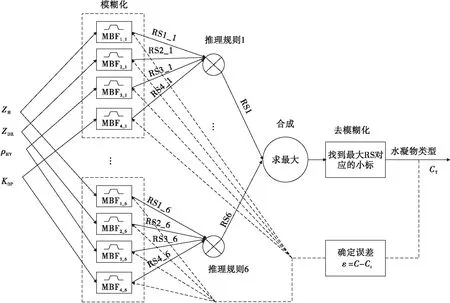
图1 模糊神经网络降水粒子分类系统框图
模糊神经网络模糊化过程就是求出降水粒子极化参数的隶属程度,钟形隶属度函数具有宽的扁平区域,区域中的最大值为1,同时该隶属度函数还具有很长的拖尾,从而提高了模糊逻辑神经网络的可靠性[13]。此外,钟形隶属度函数的导数是连续的,该特征对利用数据进行参数自动调节是很有用的,因此选取钟形隶属度函数作为模糊神经系统的隶属度函数,其表达式如式(1)所示。
(1)
其中由三个参数定义了Beta的形状,即中心点m、宽度a和斜率b,其形状如图2所示。
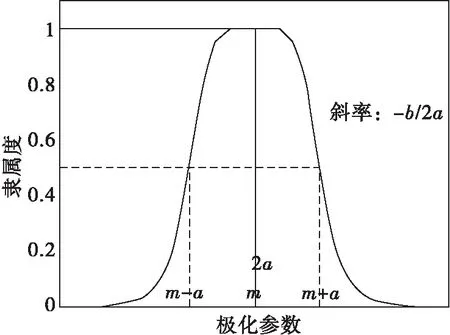
图2 钟形隶属度函数
训练过程中模糊神经网络的学习算法如下所示:将测到的雷达极化参数(ZH,ZDR,ρHV,KDP)和降水粒子类型CT设置为输入向量P。
1)将向量P输入到模糊逻辑中并得到分类的预测结果C;
2)确定输出的误差δ=CT-C;
3)如果δ=0,重复步骤1,否则根据步骤4的过程去调节隶属函数的参数;
4)只对目标结果CT和预测结果C相关的隶属函数参数进行调整,初始给定规则强度关系是RSCT
5)如果误差不为0,返回步骤1,否则停止学习过程。
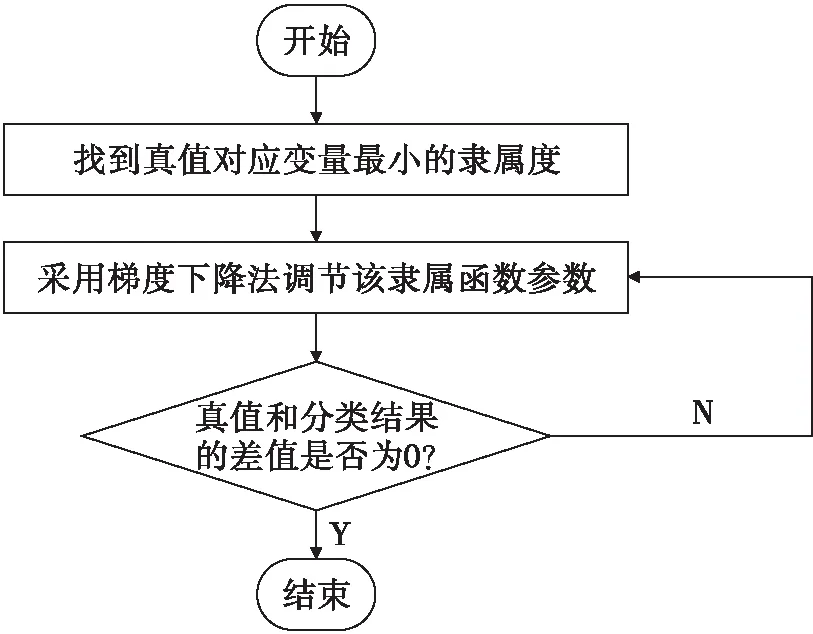
模糊神经网络训练过程如图3所示。
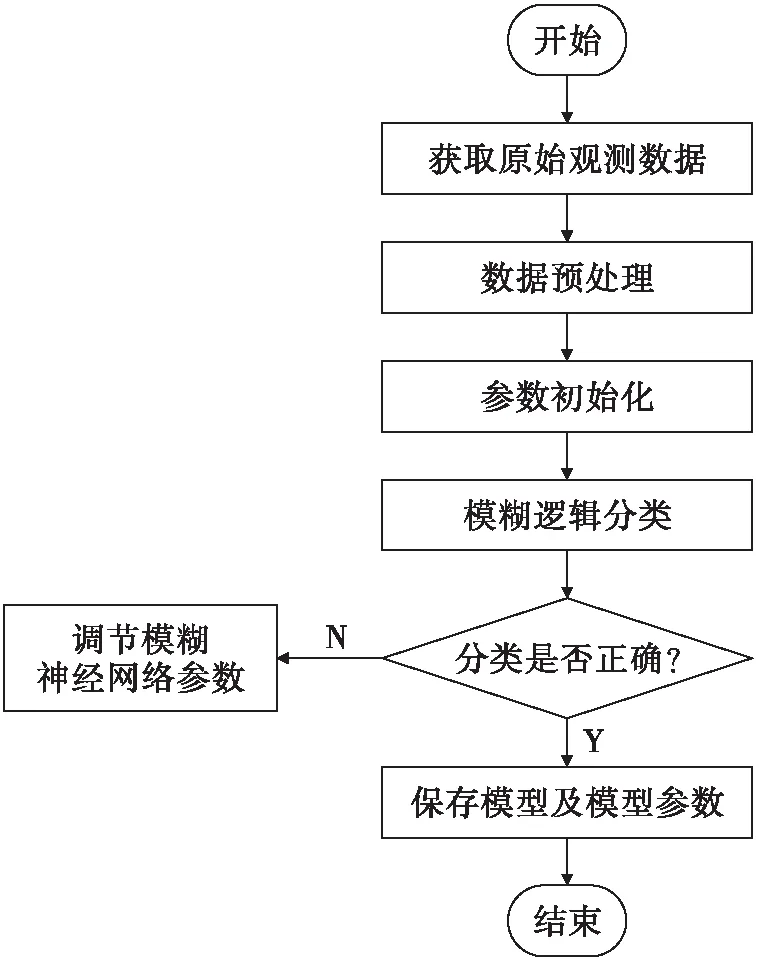
图3 模糊神经网络训练过程
参数调整方法如下:
首先从设置的隶属函数MBFi_CT(i∈[1,6])中找出隶属程度最小的值:
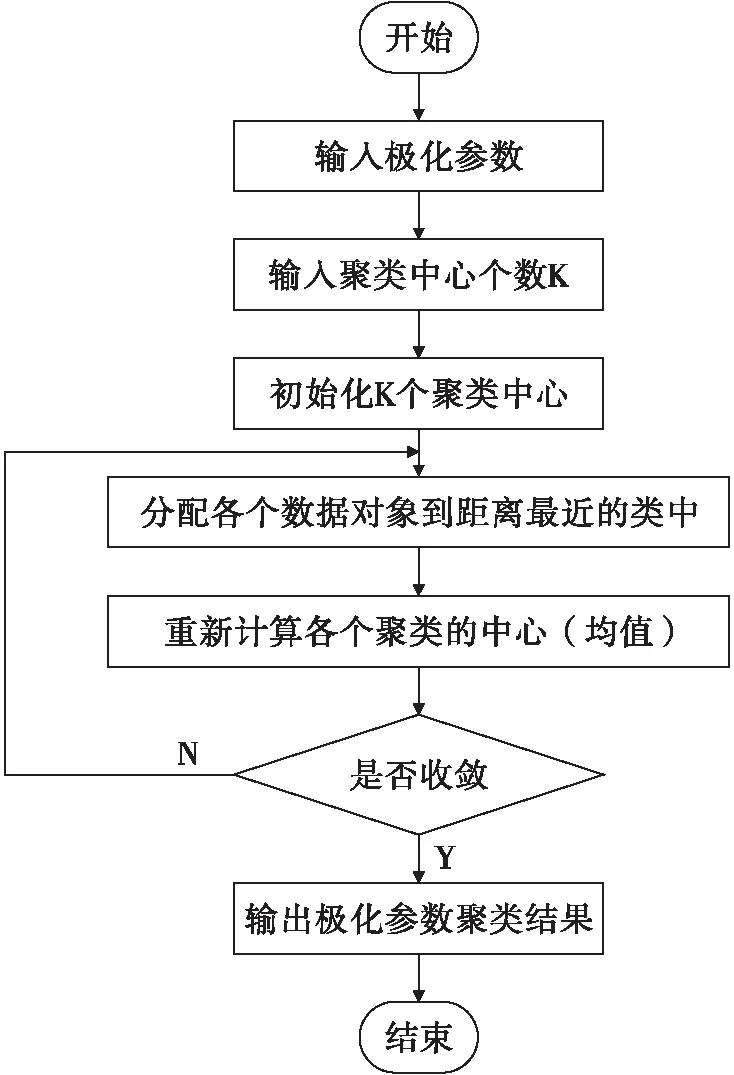
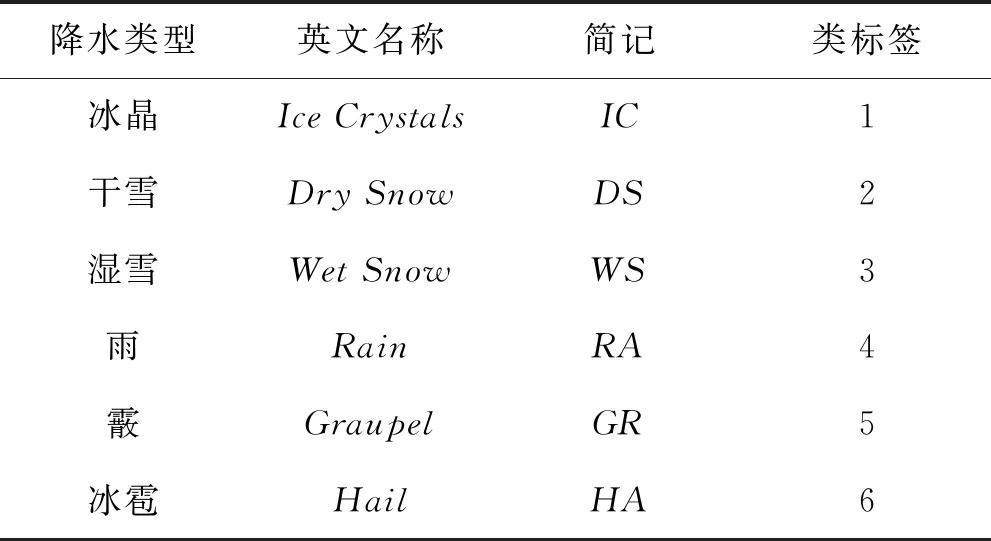
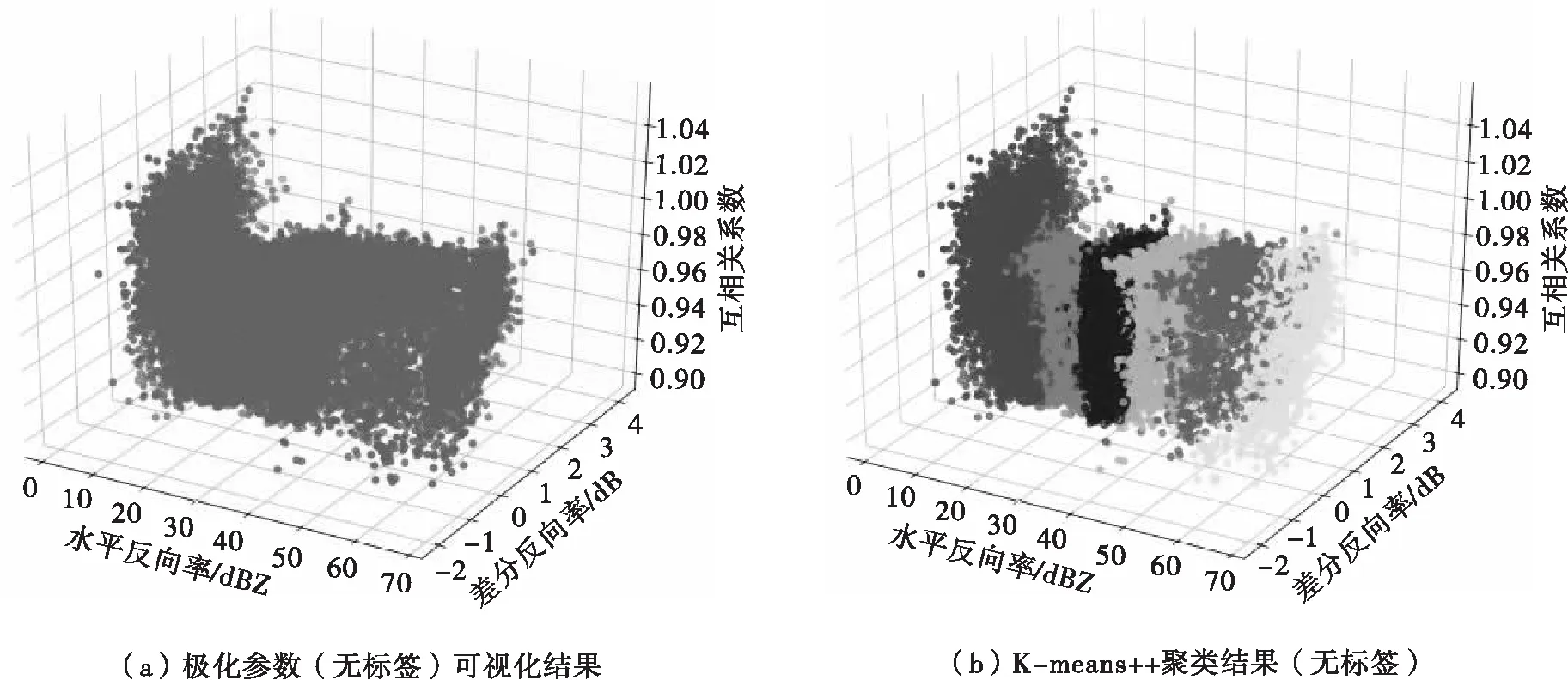
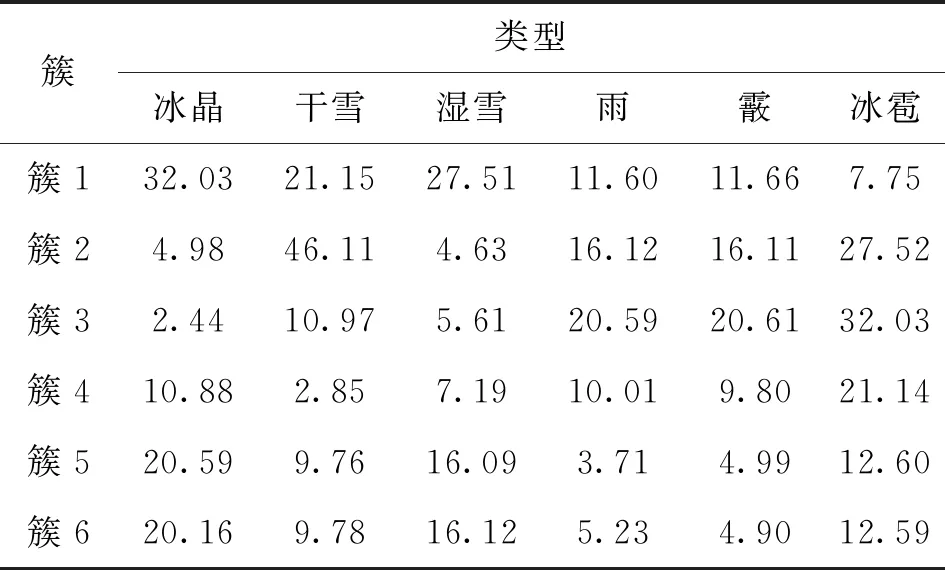
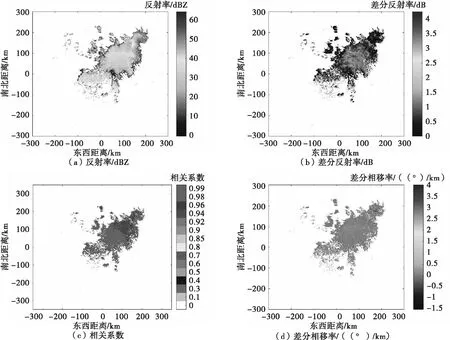
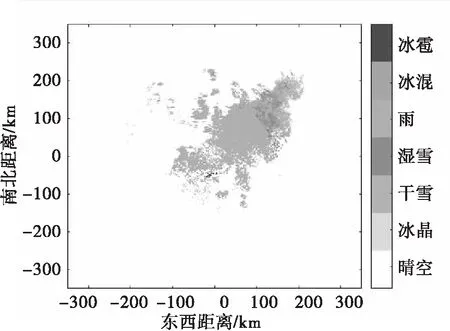
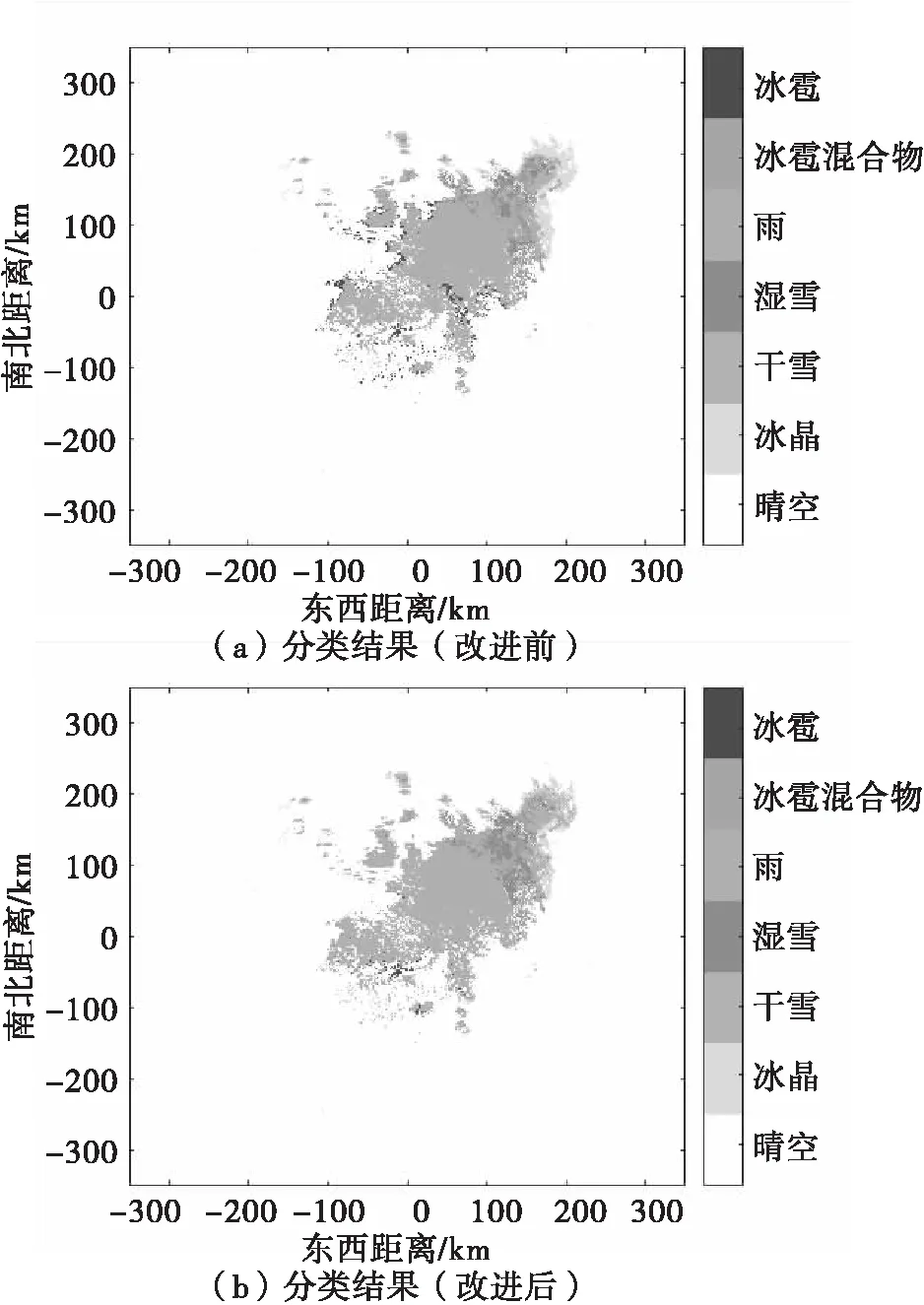
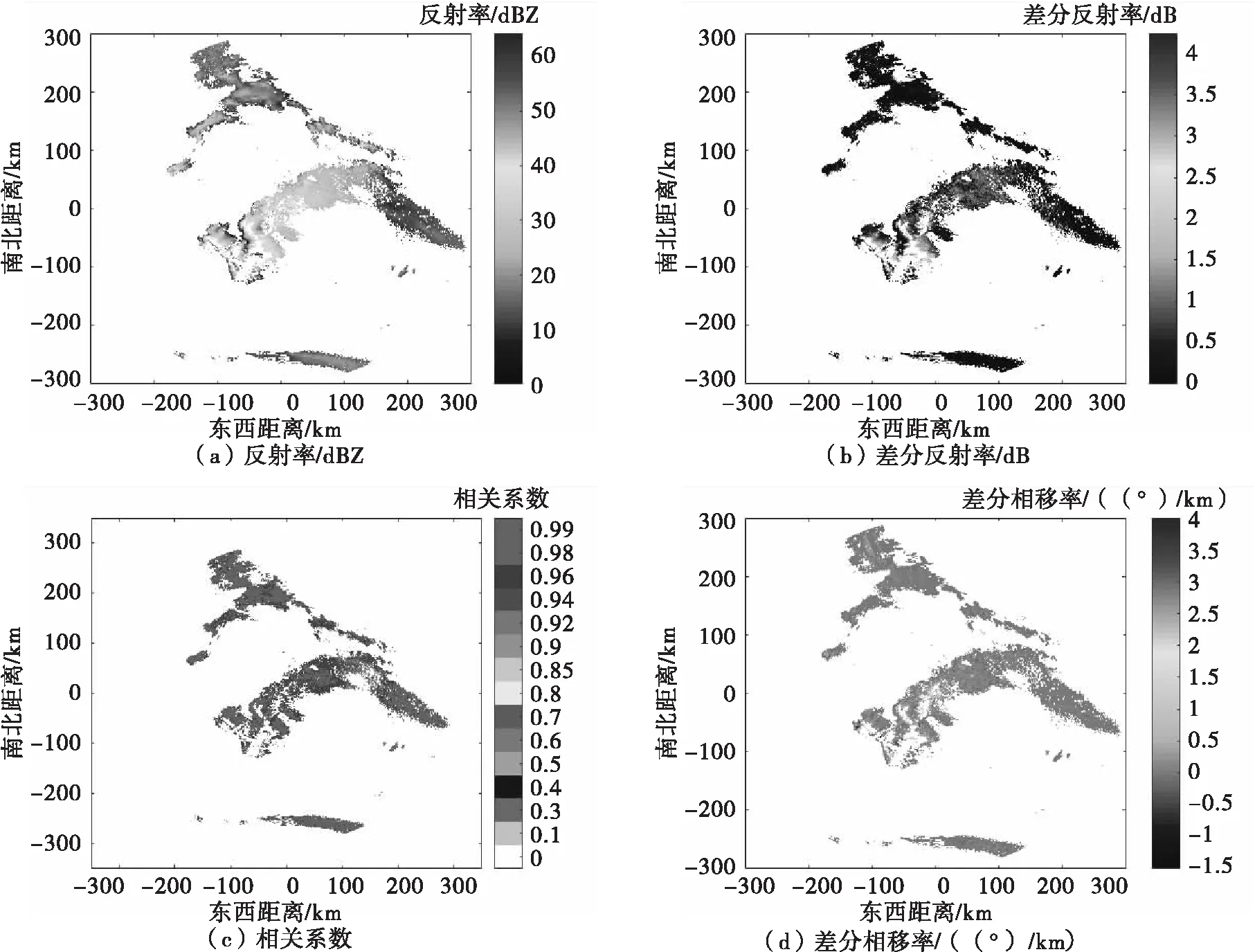
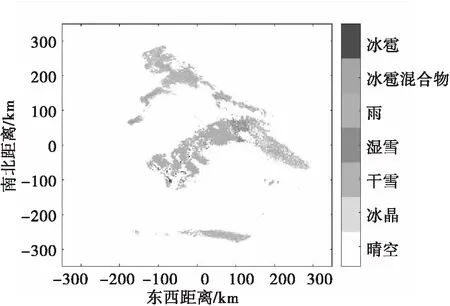
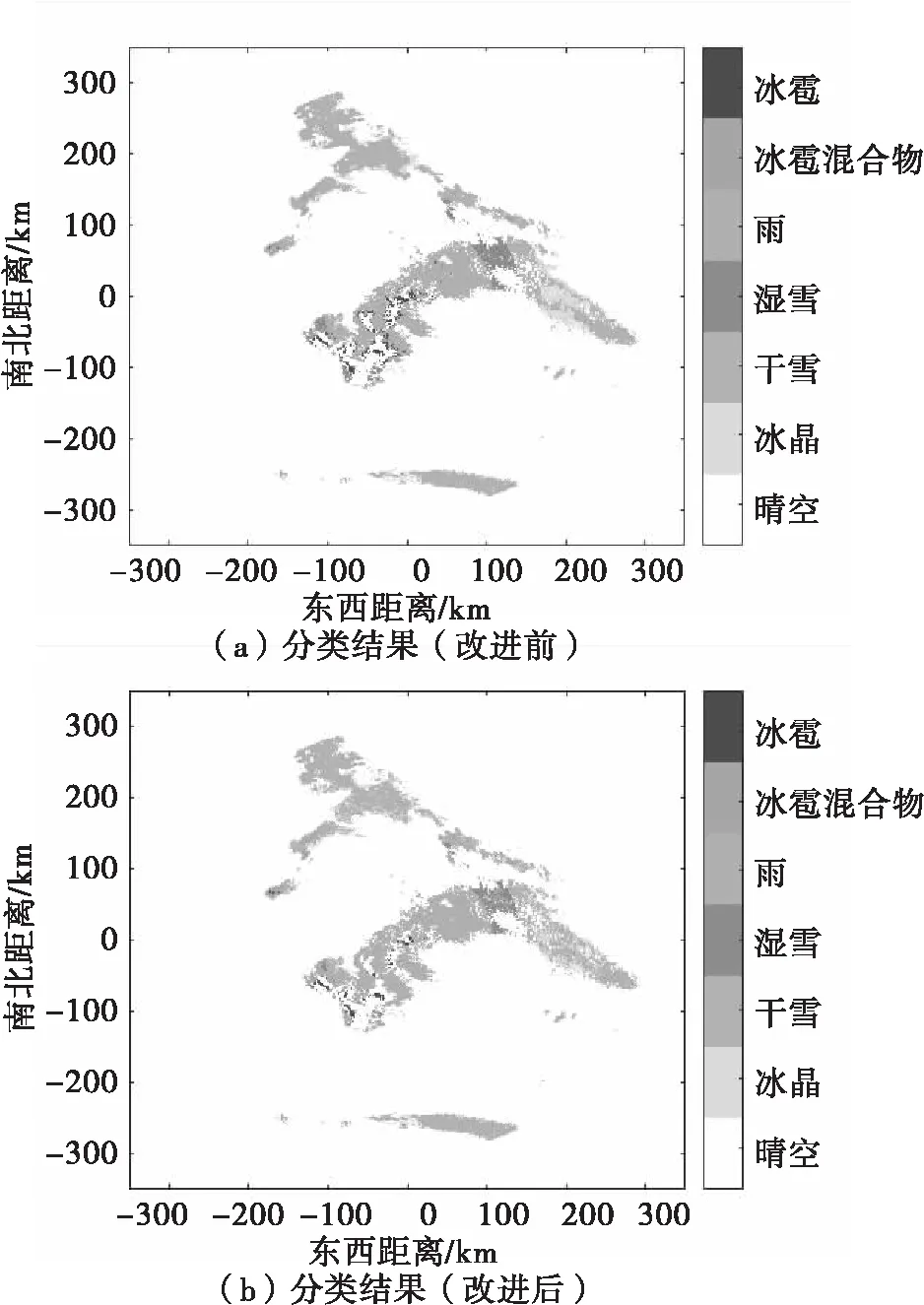
PSk_CT (2) 为了使PSk_CT朝着PSi_CT的方向调整,则参数m,a,b的更新过程如式(3)、式(4)、式(5)所示。 (3) (4) (5) (6) (7) (8) 式(8)中,xk是第k次输入变量。在得到所有的δ值后,隶属度函数的三个参数更新过程为 mnew=mold+δm (9) anew=aold+δa (10) bnew=bold+δb (11) 模糊神经网络在降水粒子分类中参数调节流程图如图4所示。 图4 模糊神经网络参数调节过程流程图 在模糊神经网络训练过程中钟形隶属度函数参数初值设置不当会出现参数不收敛、分类不准确问题。本文提出基于K-means++-MD的隶属度函数参数初值确定方法来改进模糊神经网络,该方法利用无标签区域数据聚类结果和带标签区域数据(少量)之间的相关性分析来得到带标签数据,通过对带标签数据的统计分析来得到隶属度函数初值,该初值比随机初始化的初值更加符合降水粒子对应的隶属度函数,在离线训练过程中利用确定好的初值能够得到更加稳健的模糊神经网络分类器,可以提升降水粒子识别效果。 基于K-means++-MD的隶属度函数参数初值确定流程:首先利用K-means++算法对无标签区域雷达获取的数据进行聚类,接着将聚类结果和有少量标签区域的雷达数据做相关性分析来得到带标签的数据,最后对带标签的数据进行统计分析来得到钟形隶属度函数参数初值,具体的框图如图5所示。 图5 钟形隶属度函数参数初值确定流程 1.2.1K-means++聚类 K-means算法将样本数据划分成n个具有相同方差的类来聚集数据,该算法的本质就是使数据的簇内平方和最小,因其调节的参数少、收敛速度快,已被广泛应用在很多不同领域的应用领域[14]。利用K-means算法将一组无标签区域的极化参数划分成多个不相交的簇C,用簇中样本的均值μj来描述该簇。这个均值(means)就是极化参数聚集后的“质心”。利用K-means实现双偏振气象雷达极化参数的聚类就是选择一个质心,使极化参数簇内平方和最小,计算方法如式(12)所示。 (12) K-means++算法在K-means的基础上增加了极化参数质心初始化过程,该方法能够获得有更高概率接近极化参数最终质心的初始质心[15],从而显著提升了收敛速度,比随机初始化有更好的聚类结果。利用K-means++算法聚类流程图如图6所示。 图6 K-means++算法流程图 常见的降水粒子类型有冰晶、干雪、湿雪、雨、霰、冰雹如表1所示,采用K-means++对无标签区域雷达的极化参数进行聚类,输入聚类中心个数为6,并依据极化数据自动确定6个初始的聚类中心,然后求出每组极化参数到聚类中心的距离,将数据分到离距离中心最近的类别中,然后继续计算聚类中心,当极化参数到每个聚类中心的距离不再减小,就可以得到聚类的结果。 表1 降水粒子类型 1.2.2 相关性分析 通过无标签区域聚类结果和有标签区域雷达带标签数据(少量)的相关性分析,可以得到带标签的数据,马氏距离解决了欧式距离中每个维度尺度不同和相关的问题,是另一种距离度量的方法[16]。 马氏距离也反映了协方差矩阵为Σ的两个随机变量(服从同一分布)的差异程度,极化参数样本点x,y之间的马氏距离为 (13) 用X1表示无标签区域雷达极化参数(无标签)聚类后中的一个簇;用Y1表示有标签区域雷达某一类降水粒子(有标签)对应的极化参数;利用马氏距离求出两者之间的相关性,首先求出Y1中极化参数的均值,记为μY1=(μY1,μY2,μY3,μY4),其中反射率的均值为μY1,差分反射率的均值为μY2,相关系数的均值为μY3,差分相移率的均值为μY4,再计算出Y1的协方差矩阵,计算如式(14)所示。 (14) 之后对Y1旋转至主成分进行转换,使极化参数的维度线性无关,将Y1通过坐标旋转矩阵U变换得到新的数据F,实际数据本身没有发生改变,数据F的均值向量为μF=(μF1,μF2,μF3,μF4),变化过程如式15所示。 (15) 变化后的数据维度线性无关,即每个极化参数之间维度没有关联,每个维度的方差为特征值,所以协方差矩阵ΣF是对角阵,如式(16)所示。 ΣF=UΣY1UT (16) 最后计算聚类结果X1中降水粒子样本点到重心μY1,μY2,μY3,μY4等价于计算F中降水粒子样本点f标准化后的坐标值到标准化数据重心的坐标值μF=(μF1,μF2,μF3,μF4)的欧式距离。如式(17)所示。其中x1是簇中的样本点。 (17) 计算出聚类结果中样本点到带标签数据的总距离,然后再平均就可以得到无标签区域雷达的数据聚类后每一个簇和带标签区域数据之间的距离,距离和相关性呈反比关系,距离越大相关性越差、距离越小相关性越强。重复此过程,将最小距离对应的降水粒子类型作为无标签区域雷达极化参数聚类的结果。最终可以得到带标签的数据。 1.2.3 钟形隶属度函数参数初值的确定 将获得的带标签的极化参数进行统计分析,将极化参数范围最大值和最小值和的一半作为隶属度函数参数的中心m,将极化参数范围最大值和最小值差的一半作为隶属函数的宽度a,斜率b选取8~12之间的数,最终可以得到隶属度函数的参数初值。 将上一步获取的隶属度函数参数初值带入模糊神经网络,之后利用带标签数据对模糊神经网络进行离线训练来得到稳健的降水粒子分类器,最后利用训练好的模型来实现降水粒子分类。 将极化数据(ZH,ZDR,ρHV,KDP)输入到训练好的模糊神经网络分类器来实现降水粒子分类,输入数据依次通过模糊化、规则推断、集成以及退模糊化处理,最终将输入的多个特征参数转化成单一的粒子类型。其具体实现过程如下所示: 1)模糊化 将精确的输入值转化成具有相应隶属度的模糊集合。 2)规则推断 对由模糊化得到的隶属程度进行规则推断,如式(18)所示。 IF(ZH=PSi_ jANDZDR=PSi_ jAND (18) 其中下标i=1,2,3,4表示4个测量值;j=1,2,3,4,5,6表示6种粒子类型。 3)集成 通过各个独立规则推断,分别得到了6类水凝物所对应的强度RSj,可以用叉乘运算获得“IF-THEN”规则强度,用其来衡量模糊集合的结果。 (19) 4)退模糊化 找到最大规则强度对应的索引值即退模糊化,将索引值对应的降水粒子类型作为最终识别的云降水类型进行输出。 改进的模糊神经网络在离线训练过程中隶属度函数参数能够更加稳定的自组织、自适应学习,对网络起到了反馈作用,保证了模糊神经网络降水粒子分类系统的稳定性。 基于改进模糊神经网络降水粒子分类方法具体的实现步骤如下: 1)步骤1:利用K-means++算法对无标签区域的双偏振气象雷达数据进行聚类; 2)步骤2:使用马氏距离对获取的聚类结果和带标签区域中雷达的数据(少量)进行相关性分析来得到带标签数据; 3)步骤3:对得到的带标签数据进行统计分析来得到模糊神经网络隶属度函数参数的初值; 4)步骤4:将隶属度函数初值代到模糊神经网络并进行离线训练来得到依据数据自适应调节好的分类器; 5)步骤5:利用训练好的模糊神经网络分类器实现降水粒子分类。 本次实验采用的数据来自美国国家海洋和大气管理局官方网站,选取无标签区域的数据为2016年1月1日~2018年12月1日俄克拉荷马州市KTLX雷达在降雨模式下的气象数据。带标签区域的数据来2016年4月1日~2016年6月1日马萨诸塞州的波士顿的KBOX双偏振气象雷达。KTLX和KBOX的雷达参数一致,主要参数如下:波束宽度1.25°,第一旁瓣电平-29dB,发射机的工作频率2800~3000Hz,天线增益45dB,接收机中频57.6MHz,波长10cm,脉冲重复频率250~1200Hz,带宽0.3MHz,径向的分辨率250m。 首先对选取无标签区域数据进行聚类,图7(a)为数据没聚类前的可视化结果,图7(b)为无标签区域数据经过K-means++聚类后的结果,聚类后的簇用不同的颜色来表示,每一种颜色代表一类簇。 图7 接着利用马氏距离对KTLX雷达聚类结的每一簇和KBOX雷达的带标签的数据进行相关性分析,结果如表2所示,表中第一列为聚完后结果,第一行为降水粒子的类型,中间数字部分为每个聚类结果和降水粒子之间的马氏距离(无量纲)。 表2 相关性分析结果 通过表2可以看出聚类结果和降水粒子之间的关联程度。例如,在表中第二行簇1和冰晶之间的距离为32.03,距离最大则相关性最小,和冰雹的距离是7.75,距离最小则相关性最高。因此,将簇1分成冰雹,同理,可以看出簇2为湿雪,簇3为冰晶,簇4为干雪,簇5为雨,簇6为霰,通过相关性分析可以对KTLX雷达数据打上标签。 对获取的带标签的数据进行统计分析,得到的隶属度函数参数如表3所示。 表3 钟形隶属度函数参数初值 将得到的隶属度函数参数初值代入模糊神经网络进行离线训练,利用训练好的模糊神经网络系统进行降水粒子分类,为了验证改进后模糊神经网络的性能,选取KTLX雷达在2019年6月19日14时55分和2020年4月22日05时06分两个典型强对流天气的极化数据对模糊神经网络系统进行测试,2019年6月19日14时55分的极化参数的可视化结果如图8所示,分类结果(NOAA提供)如图9所示,不同的颜色代表不同的降水粒子类型。 图8 KTLX雷达获取的极化参量(2019年6月19日14时55分) 图9 NOAA提供分类结果(2019年6月19日14时55分) 极化参数经过模糊化、规则推理、集成、去模糊化得到最终的分类结果,图10给出了模糊神经网络改进前和改进后的降水粒子分类结果。 通过图9和图10的对比可以看出,改进后的模糊神经网络减小了雨误判为冰雹的范围,提高了冰雹识别率;在较高区域中干雪识别范围增大,减小了干雪错判成冰晶的概率,晶体的识别效果更加精细;湿雪和霰的识别结果与实际融化层中的粒子类型分布情况更加符合,通过这组极化数据的测试结果可以看出改进后的分类结果与实际的云降水粒子类型更加相似。 图10 降水粒子分类结果 另一组测试数据(2020年4月22日05时06分)极化参数的可视化结果如图11所示,分类结果(NOAA提供)如图12所示。 图11 KTLX雷达获取的极化参量(2020年4月22日05时06分) 图12 NOAA提供分类结果(2020年4月22日05时06分) 将这组测试数据分别通过改进前和改进后的模糊神经网络系统,得到的降水粒子分类结果如图13所示。 图13 降水粒子分类结果 从图12和图13的比较中可以看出改进后的分类结果中雨误判为冰雹的区域减小,提升了冰雹识别的可靠性;在融化层上面冰晶和干雪的识别结果比改进前的结果更加合理;雨和冰雹交界区域的湿雪明显减少,与实际结果更加符合;融化层附近有雨区的出现,提升了雨的识别效果;霰的识别范围基本没发生变化。通过这组数据处理表明,改进后网络能够准确地识别出降水粒子的相态。 总体来说,改进后的模糊神经网络分类结果与实际降水粒子类型更加符合。 针对模糊神经网络在训练过程中隶属度函数初值不易设置的降水粒子分类问题,本文提出了一种改进的模糊神经网络方法,该方法首先利用K-means++算法对无标签区域双偏振气象雷达获取的数据进行聚类,其次通过马氏距离对聚类结果和另一区域雷达的少量带标签数据进行相关性分析来得到带标签数据,然后将获取的带标签极化参数范围最大值和最小值和的一半作为隶属度函数参数的中心m,将极化参数的最大值和最小值差的一半作为隶属函数的宽度a。将经过统计得到的参数初值代入模糊神经网络中并对网络进行离线训练,训练结束后能够得到依据数据自适应学习好的网络,最后利用训练好的模型完成降水粒子分类。实验结果表明,改进后的模糊神经网络方法能够获得更为精确的降水粒子分类结果。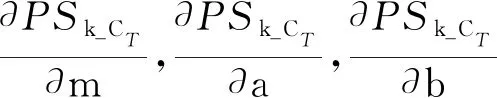
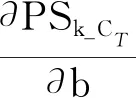
1.2 基于K-means++-MD的隶属度函数参数初值确定方法

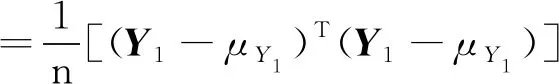
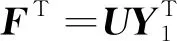
1.3 降水粒子分类过程
KDP=PSi_ jANDρHV=PSi_ j)
THEN hydrometeor=j2 算法流程与步骤
3 实验算法验证

4 结束语

