基于快速码根检验的RS 码综合识别算法

张晓林，李修桥，孙溶辰

（哈尔滨工程大学信息与通信工程学院，黑龙江 哈尔滨 150001）

0 引言

通信系统中，信道编码技术实现了在信息层面对数据进行检错和纠错。RS（Reed-Solomon）码是一种多进制信道编码，其由于编码特性具有较强的抵抗突发错误的能力，因此被广泛应用于深空通信和卫星通信。在认知无线电领域，信道编码识别是通信侦察和截获的重要环节。如何在复杂的信道环境下根据截获的信息快速、准确地恢复编码参数是关键问题。对于RS 码的盲识别问题，目前的识别算法依据是否需要先验信息可分为硬判决和软判决两大类。硬判决算法以排除不可能事件为中心思想设置适当阈值；软判决需要确定信噪比，并在特定的调制方式下由信噪比转化为误比特率，进而推导较准确的阈值，两者各有优缺点。

RS 码具体的识别算法包括高斯消元法[1-2]、欧几里得算法[3]、基于伽罗华域傅里叶变换（GFFT,Galois field Fourier transform）算法[4-7]、基于中国剩余定理算法[8]、码根检验算法[9-11]等。高斯消元法通过分析矩阵秩的情况识别码长，适用于低误比特率情况；欧几里得算法将码字多项式辗转相除，依次识别码长和生成多项式，需要存在足够多的正确码字；基于中国剩余定理算法将编码映射为环上的线性码，依次识别码长和本原多项式，算法复杂度低，但性能较差；基于GFFT 算法和码根检验算法本质上都是基于有限域校验矩阵寻找连续码根，可以实现对码长、本原多项式和纠错能力的联合识别，性能较好，但是该类算法基于有限域进行计算，复杂度高。

近些年，相关算法主要改进GFFT 和码根检验。文献[12]实现在二元域的识别，先通过本原元检验筛选，再判断连续的偶数码根，降低了计算复杂度，但是阈值兼容性不高。文献[13]通过前2 个码根筛选，再通过GFFT 进行识别，但识别过程仍然存在较高的虚警概率和漏警概率。文献[14]提出纠正单比特错误码字，但前提是需要预先得知码长，且计算量较大。文献[15]提出一种基于平均余弦符合度的二进制循环码识别方法，利用软判决序列度量奇偶校验关系。文献[16]提供了正确识别生成器多项式因子的概率下界。文献[17]推导并分析了多种调制方式下的RS 码和交织器的联合识别。

目前，码根检验算法识别性能较好，但复杂度仍有待降低，并且大多数算法基于遍历各种参数最终选取最优解，需要同时兼容不同长度的编码，会牺牲不同长度编码的特性，导致整体识别概率不高。本文提出一种快速码根检验算法，利用组合码根进行检验，并将RS 码划分为短码和长码分开识别。首先，在短码情况下，降低随机序列和相同级数不同本原多项式的RS 码对算法的影响，通过组合码根检验综合考虑通过判定的参数，降低漏警概率；然后，对长码直接使用码根检验，快速定位参数。算法使用的校验矩阵以二进制比特数据形式存储，识别过程基于二元域，计算量小，速度快；另外，该算法不需要获取先验信息，当信道条件未知时能以较高的性能完成识别。

1 RS 码原理及其性质

定义1[18]伽罗华域GF(q)(q＞ 2)中，本原元为α、码长为n=q-1的本原BCH 码为RS 码。

RS 码是多进制编码，其编码域为GF(2)的扩域GF(2m)，通常m∈ [3,8]。若本原多项式为p(x)，则可以表示为。定义(n,k)RS码，n为码长，k为信息位长度，纠错能力为t。非缩短RS 码满足n=2m-1,n-k=2t，生成多项式通常为

其中，n为码长，2t为校验位数量。

根据定义2 和定理1，无错RS 码的谱多项式有连零成分，因此RS 码识别问题可转化为在未知编码参数的条件下，通过分析矩阵ΦN×2t中零元素的分布情况，识别编码域级数m、码长n、信息位长度k、本原多项式p(x)以及生成多项式g(x)。

2 RS 码快速码根检验识别模型

2.1 模型假设与构建思路

RS 码的参数识别算法通常有如下假设。1) 截获的编码序列已完成帧同步，信噪比、误比特率等先验信息未知，不参与算法的计算过程。2) 编码类型为非缩短RS 码，即码长n=2m-1。3) 信息位k=1的(n,1)RS 码校验位较冗余，码率极低；当7 ≤m≤ 8时，t=1的(n,n-2)RS码纠错性能较弱。因此，(7,1)、(1 27,1)、(2 55,253)等参数的RS 码在实际应用中很少使用，本文不予考虑。

基于RS 码编码特点，建立如下数学模型。设截获的编码序列参数为(2m- 1,k)RS 码，码字数量为N，首选设置编码域GF()，将其转换到二进制，按行排入N×mx(-1)的识别矩阵中，Nx为待识别码字的数量，满足

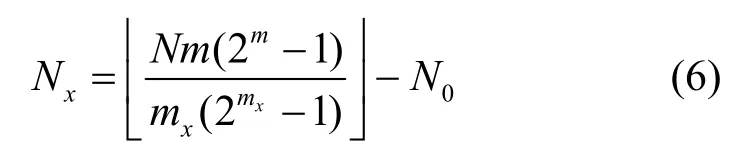
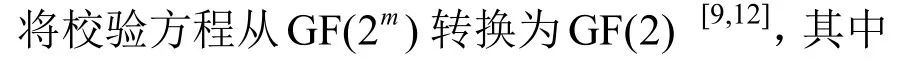
上述码根检验算法较冗余，并且算法在短码情况下容易受相同级数m、不同本原多项式p(x)的影响，当通过判决阈值时直接完成识别会造成漏警。针对以上问题，本文从减少码根检验计算量和降低识别漏警概率2 个角度展开分析。

2.2 快速码根检验算法

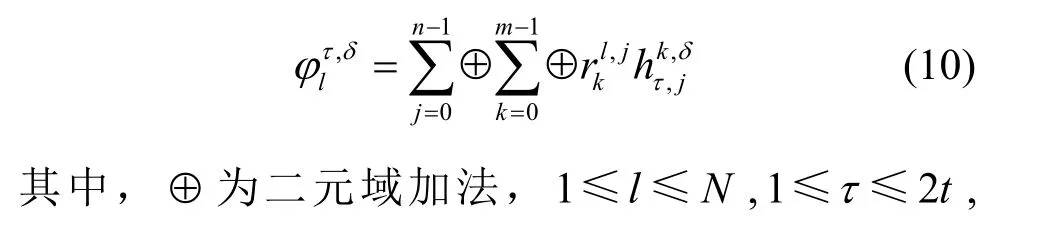
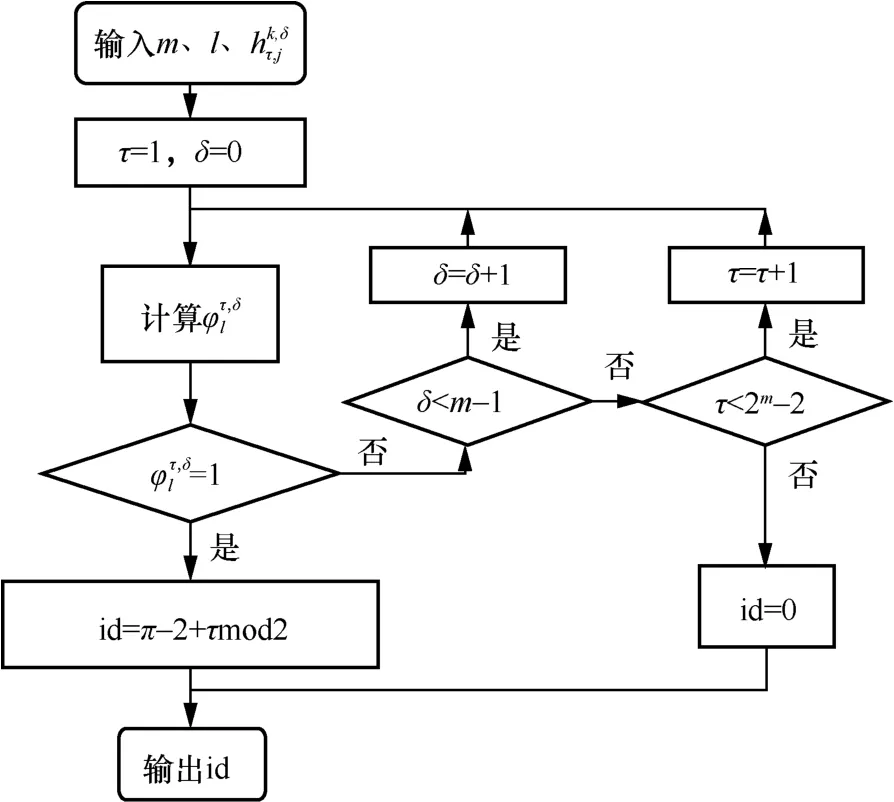
图1 连续偶数码根的快速检验算法流程

2.3 码根阈值选取

当编码域设置错误时，由于信息位与校验位的校验关系被打破，按照当前参数形成的待识别码字可等同于随机序列，每个比特之间取值0,1 相互独立，因此可得

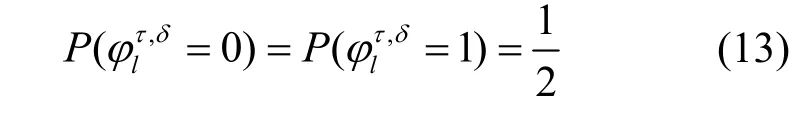
对 {α α2}和 {α3α4}检验分别设定恰当的阈值Th1和Th2，用于排除绝大多数随机序列的干扰，随机序列通过 {α α2}和 {α3α4}检验的概率分别为

设Nx个码字中可通过 {α α2}和 {α3α4}检验的数量分别为w1和w2。由定理2 可知，若m x≠m，当前码字为近似随机序列，则w1和w2符合二项分布wi～B(N x,pi)，参数分别为

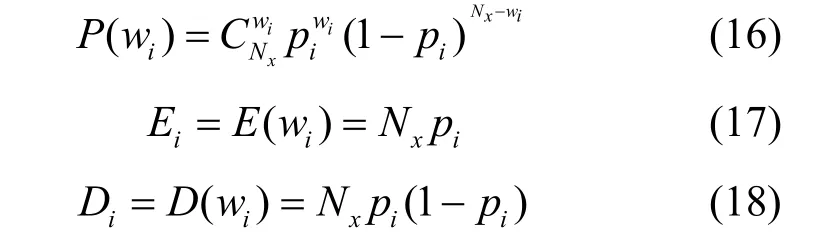
其中，E i和Di分别为wi(i= 1,2)的均值和方差。每个码字是否通过 {α α2}或 {α3α4}检验之间相互独立，由中心极限定理可得，当Nx足够大时，w1和w2的分布趋向于参数为E i和Di的正态分布，即wi～N(Ei,Di)。设定一个较高的阈值Thi，则

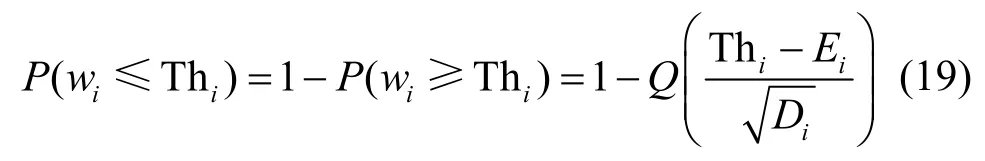
其中，Q(x)为Q函数，即

下面，以长度等同于(7,3)RS 码的随机序列为例，设置数量Nx= 1000，蒙特卡罗仿真1 000 次，得到随机序列通过码根检验的数量占比和拟合正态分布曲线如图2 所示。

图2 w1 的概率分布曲线和拟合正态分布曲线

图2 中拟合正态分布曲线的均值E1=15.625，方差D1=15.380 9，当设置Th1为28 时，数量大于或等于Th1的码字概率小于0.135%，可以将大部分随机序列剔除，将大部分t=1的RS 码筛选出来。但是，仅靠阈值Th2不能准确地选取t≥ 2的RS 码，原因如下。由性质1 可知，即使在无误码情况下，t=1的RS 码部分许用码字也可以通过 {α3α4}检验使w2≥ Th2。因此，需要同时统计通过 {α α2}和{α3α4}检验的数量，选取通过检验的数量与阈值差值最大的参数作为最终结果。

当信道条件较好时，正确参数的码字通过{α α2}和 {α3α4}检验的数量远大于Thi，为降低计算复杂度，仍需要设置一个极高的阈值Th3，当通过检验的数量超过该阈值时，直接判定该参数为正确参数。设定当P(w1)＜p3=10-5时对应的最小码字数量为阈值，即Th3=35，对应的概率小于10-5。

2.4 算法步骤

算法整体思路如下。赋予长码较高的置信权重，对短、长码分别遍历编码域，进行参数判定。对于短码，若通过 {α α2}检验的码字数量超过Th3，则直接判定当前参数；否则，继续遍历，将m下的所有本原多项式进行综合考虑，判断所有参数的{α α2}、{α3α4}检验是否分别通过阈值 Th1、Th2，若通过则作为待定参数。对于长码，若某一组参数的 {α3α4}检验通过阈值Th2，则直接判定为该参数；否则，选取短码的待定参数作为识别结果。具体步骤如下。

输入长度n（2）=Nmnbit 的二进制编码序列、二元域校验矩阵hτ,j

1)pλ不等，idλ相等。取最小值对应的Pλ，其参数下的编码为随机序列的可能性更低。

2)pλ相等，idλ不等。依据性质1，若idλ差值为1，较大idλ值对应的d有可能来源于许用码字重叠，但由于两者d相等，这种概率几乎为零，因此选取较大idλ值和其对应的pλ，其参数下的编码为随机序列的可能性更低。

3)pλ不等，idλ不等。同情况2)，选取较大idλ值和其对应的pλ。

步骤1 中，当短码通过较高的阈值Th3或者长码通过Th2时直接判定当前参数。当对应多个id0时，同步骤4 中情况3)，选取较大的id0值和其对应的p0。

步骤6 中，选取待定参数集合中与阈值差值最大的参数作为最终结果，若最大差值对应的参数不唯一，选取步骤3 和步骤4 中和较大的对应的参数作为最终参数，如图3(d)所示。

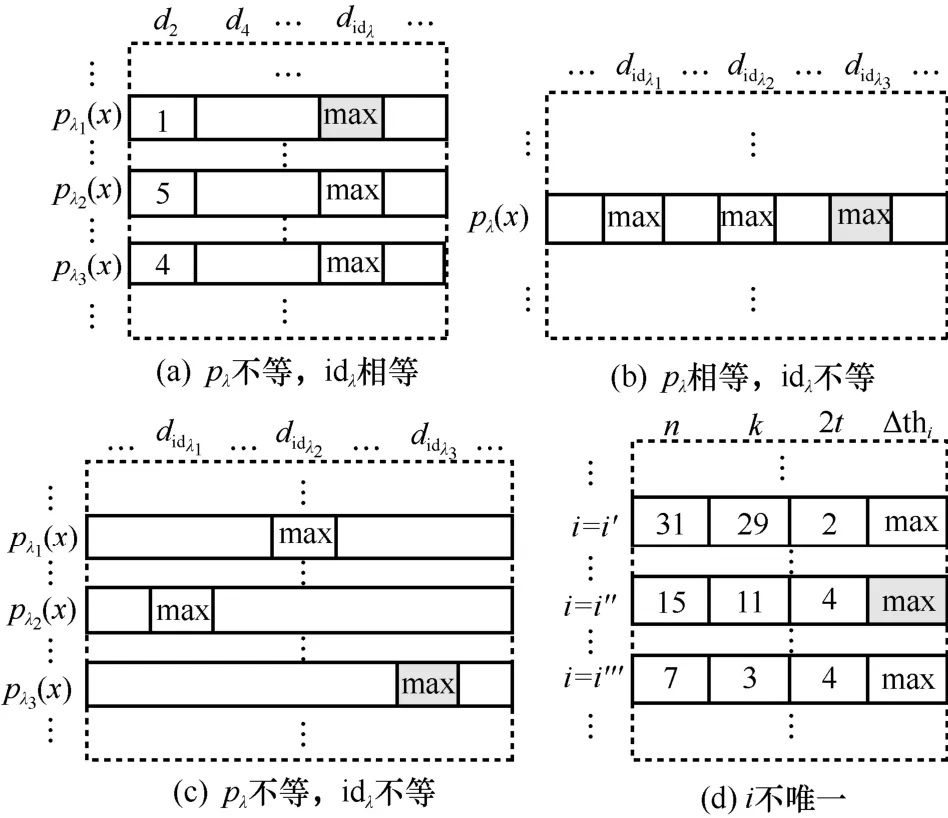
图3 非单一最大值的选择策略

RS 码识别流程如图4 所示，其中，产生待定参数部分对应步骤3 和步骤4，即选取通过检验的数量与阈值的最大差值对应的参数。

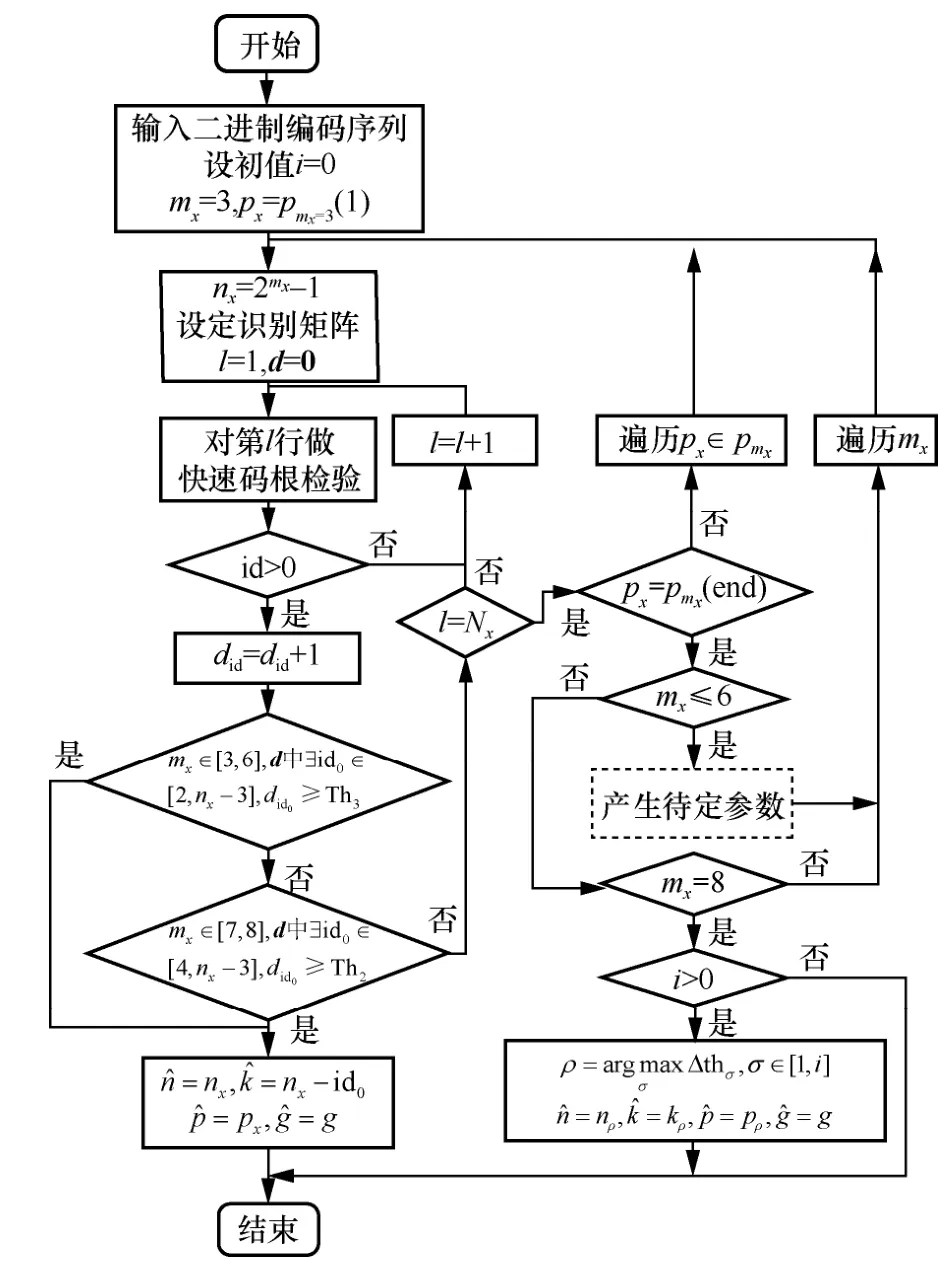
图4 RS 码识别流程

3 仿真验证与分析

3.1 仿真验证

仿真设定分别生成1 000 组RS 码，参数设置如表1 所示。首先以(7,5)RS 码为例，加入误比特率为0.03 的错误比特，设立识别矩阵，当遍历到mx=3,p x(x)=x3+x+1时，识别矩阵的所有行对应的连零矩阵的偶数分布向量为d=(462,2,0)，其中d2= 462大于实际中算法设定阈值Th3=35，所以当遍历到d2=35时即可完成识别，求出连续根为α,α2，由连续根个数为2，求得码长n=7，信息位长度k=7 -2=5，g(x)=(x-α)(x-α2)=x2+α4x+α3，识别正确。

表1 RS 码参数设置、本原多项式和生成多项式

然后，以(31,27)RS码为例，加入误比特率为0.03 的错误比特。由于当m x＜m时，Nx＞ 1000，因此仿真时取N′= min(1000,Nx)。由于码长增加，正确码字减少，经计算后所有参数均未通过阈值Th3，由阈值 Th1和 Th2得到几组待定参数，如表2所示。当遍历到mx=4,p x(x)=x4+x+1和mx=5,px(x)=x5+x4+x3+x2+1，以及mx=5,px(x)=x5+x2+1时，d中分别存在通过对应阈值 Th2,Th1,Th2的元素，将三组参数作为待定参数，并分别计算d与阈值的差值，得到 Δth1,Δth2,Δth3分别为0,1,3，显然最大值为Δth3，对应的元素为d4，因此最终识别参数为m=5,p(x)=x5+x2+1,n=31,k=31 -4= 27,g(x)= (x-α)(x-α2)(x-α3)(x-α4)=x4+α24x3+α19x2+α29x+α10，识别正确。

表2 (31,27)RS 码识别待定参数

同理，设置误比特率为0.004，识别(127,119)RS码，当遍历到mx=7,p x(x)=x7+x3+x2+x+1时

3.2 性能分析

由式(12)计算等效的GF(2)校验矩阵元素，算法计算量主要源于二元域加法。求解一次的模2加运算量为wτ,δ，其中1 ≤τ≤n-1,0 ≤δ≤m-1。将不同取值的τ,δ进行平均化处理，通过仿真得到不同级数m下的如表3 所示。

表3 不同m 下的

表3 不同m 下的

当级数m设置错误时，由式(13)可知码根快速检验的平均模2 加计算量为

若级数设置正确，即m=m0，分析误比特率对算法运算量的影响。低误比特率情况下，由于阈值Th3的设置，当通过检验的数量达到阈值后停止识别。设停止识别前含错误比特的码字数量为Ne，无错码字数量为Th3(m)，则 0≤Ne≤N- Th3(m0)，含错码字平均模2 加计算量为T0(m0,Ne)，无错码字模2 加计算量为

最坏情况下，所有编码都是最后一个本原多项式，则算法总的模2 加计算量为

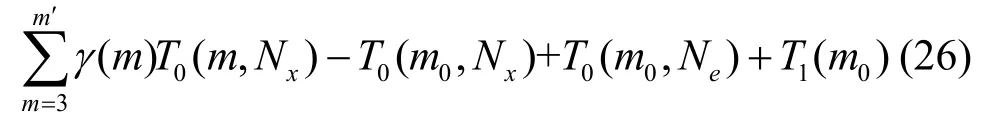
其中，γ(m)为级数m下的本原多项式数量，m′=m0。同时，考虑到更新向量d的计算量，以及步骤4 的求和计算量T2(m)=2m-1-3，最坏情况下，存在单纠错和多纠错情况共8 个待定参数，因此加法计算量为

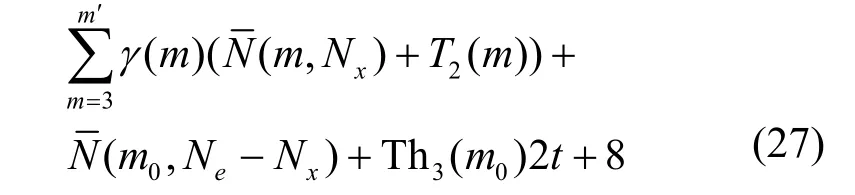
对于高误比特率情况，最坏情况下正确参数的编码数量恰好接近临界值Th3，需要遍历所有短码，此时有

算法完成识别的理论上限是编码序列中存在至少一个正确码字。设编码序列的误比特率为ε，则码字无错误比特的概率为(1-ε)mn，编码序列中存在至少一个无错误比特码字的概率为

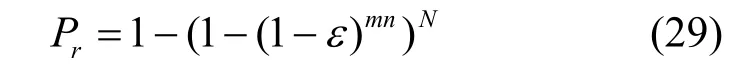
其中，N为编码序列的码字数量，原理上算法的识别概率P≈Pr。设置存在正确码字的概率为Pr≥ 0.99，则可以得到不同误比特率下算法实现99%以上识别率所需的最少码字数量，如图5 所示。当误比特率增加时，所需码字数量快速增加，理论上，只要码字数量足够多就可以完成识别，但实际中获取的码字数量有限。

图5 不同误比特率下算法实现99%以上识别率所需的最少码字数量

以数据存储和深空通信中常用的编码类型，包括(7,3)RS 码、(15,9)RS 码、(31,15)RS 码、(63,57)RS 码、(127,111)RS 码和(255,223)RS 码为例，随机选取本原多项式，仿真产生每种编码各1 000 组码字，并加入错误比特，蒙特卡罗仿真500 次，根据式(29)得到算法识别率曲线和正确码字存在概率曲线，如图6 所示。图6 中，实线为实际仿真的识别概率P，虚线为正确码字存在概率Pr，即识别上限。由图6 可知，当信道环境变差，或码长增加时，正确码字数量锐减直至为零。由于设置了组合码根检验并综合分析待定参数，本文算法极大地降低了漏警概率，当级数4 ≤m≤ 8时，识别率P与Pr曲线基本重合；当级数m=3时，由于码长较短，随机序列和相同m不同p(x)的RS 码容易通过 {α α2}和 {α3α4}检验，因此识别率P与Pr有差值。

图6 RS 码识别率曲线和正确码字存在概率曲线

仿真不同纠错能力对算法识别率的影响。以码长n=31为例，分别设置不同t值的1000 组编码，并加入错误比特，蒙特卡罗仿真500 次，(31,31 -2t)RS 码识别率曲线和正确码字存在概率曲线如图7 所示。由图7 可知，纠错能力t≥2的RS 码的识别率P与Pr曲线基本重合，由此可知算法受码率的影响较小，稳定在临界值附近；t=1时的(31,29)RS 码校验位较少，码率较高，编码与随机序列的差异性小，识别率P与Pr有差值，但仍能在误比特率为0.03 时达到99%的识别率。

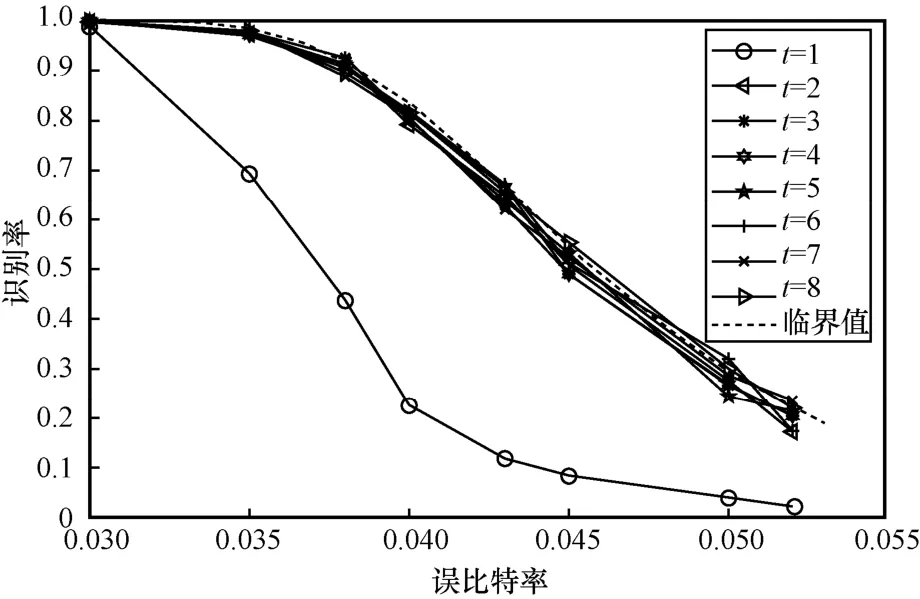
图7 (31,31 -2 t)RS 码识别率曲线和正确码字存在概率曲线

3.3 其他算法对比

首先，对比算法计算量，包括文献[4]算法、文献[12]算法和文献[13]算法。若正确级数为m0，文献[4]算法对所有码字做GFFT，模2 加计算量为

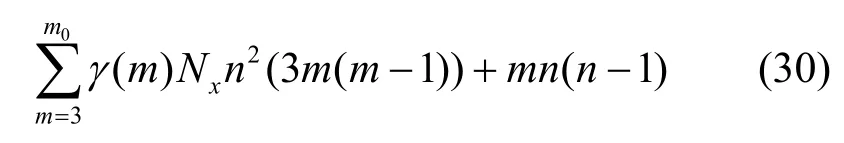
文献[12]算法经过一次码字剔除后剩余码字数量为，模2 加计算量为

文献[13]算法经2Nx次码根检验后对Ngn个码字做GFFT，模2 加计算量为

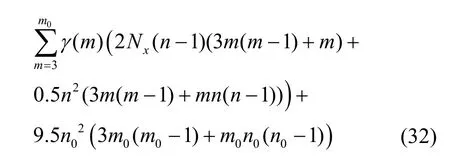
设置码字数量为1 000，统一使用图6 中的6 种RS 码，误比特率分别为0.02、0.01、0.005、0.002、0.001 和0.000 4。假设在最坏的情况下，本原多项式为最后一项。将加法计算量等同于模2 加计算量，不同级数m下的算法复杂度对比如图8 所示。由图8 可知，算法模2 加计算量随级数m增大呈指数级增加。低误比特率下，由于使用快速码根检验算法，本文算法复杂度相比同类算法明显降低，无论短码还是长码都可以用较低的计算量完成识别。随着误比特率增大，本文算法为降低漏警概率提高识别精度，需要遍历短码的全部本原多形式，计算量逐渐增加，并接近长码的计算量，级数m=3,4时高于文献[12-13]算法的计算量。

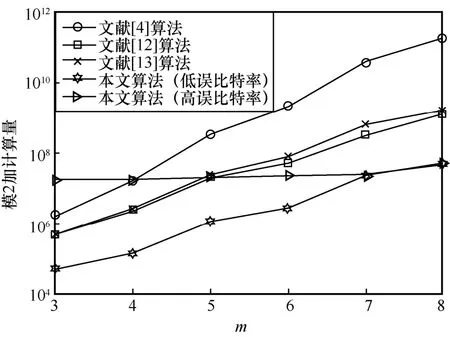
图8 算法复杂度对比

然后，仿真并分析文献[12-13]算法和本文算法的漏警概率。在对某一特定的RS 码进行识别时，存在识别正确、识别错误和未得出识别结果3 种情况，将其概率值分别设为P,Perr,Pnull，则漏警概率Pmiss=Perr+Pnull。以(7,3)RS 码、(15,9)RS 码这2 种短码为例，在不同误比特率下进行500 次蒙特卡罗仿真，得到算法的漏警概率对比如图9 所示。由图9可知，本文算法可在高误比特率下将部分未识别的结果正确识别，与文献[13]算法相比，本文算法虽然错误识别的数量小幅度增加，但整体的漏警概率降低。

图9 算法漏警概率对比

最后，对比本文算法与以上几种同类算法的识别率。以(7,3) RS 码、(31,15) RS 码 和(255,223)RS 码为例，设置码字数量为1 000，分别在不同的误比特率下进行500 次蒙特卡罗仿真，得到不同算法识别率对比如图10 所示。由图10 可知，本文算法的识别率好于其他3 种算法。文献[12]算法通过校验和的统计特性设置阈值，并将编码域和生成多项式分开识别，第一步判决虚警概率和漏警概率都较高；文献[13]算法在短码情况下容易受随机序列影响，漏警概率高。本文算法通过两组码根检验，并综合分析待定参数，因此识别性能明显好于文献[12]算法，在短码情况下较文献[13]算法更优。

图10 不同算法识别率对比

4 结束语

本文从降低码根检验角度出发，提出了 一种快速码根检验算法，并将RS 码划分为长码和短码，通过组合码根检验综合分析待选参数，最终完成级数、本原多项式和生成多项式的联合识别。本文使用的综合识别算法在相对较低的复杂度下降低了识别漏警概率，实现了较好的识别性能，并且在高误比特率环境下依然能够完成识别。本文算法不需要信道先验信息，因此适用于多种信道环境，具有较好的工程实用性。本文算法的代价是需要提前存储二元域校验矩阵，牺牲存储空间以加快识别速度；同时，在信道环境较恶劣时，通过牺牲一定的算法复杂度以提升短码的识别性能。