基于回声状态网络的锂离子电池SOC估算*

陈 丽

（1.兰州理工大学电气工程与信息工程学院 兰州 730050）（2.甘肃省先进工业过程控制重点实验室 兰州 730050）（3.兰州理工大学电气与控制工程国家级实验教学示范中心 兰州 730050）

1 引言

锂电池因其容量大、质量轻、高能量密度以及长循环寿命等突出品质而持续帮助锂电池在电动汽车储能设备市场上占据主导地位［1］。为保证锂离子电池的动力性和安全性需要一套完善的电池管理系统（Battery Management System，BMS）对其进行有效的控制和管理。其中，电池的荷电状态（State of Charge，SOC）能够反映电池的能量状态，获取准确的SOC值是实现对BMS的基础［2～3］。准确地估算SOC能提高电池的利用率和延长电池的使用寿命，防止其出现过充或放电现象。考虑到锂电池本身复杂电化学特性，SOC无法直接测量，而且SOC与电池电压、电流、温度等参数间表现出强烈的非线性关系［4］，使得准确估算SOC是一大挑战。

常用的SOC估计方法有传统估计法、基于模型的方法以及基于数据驱动的方法。其中，传统估计法有开路电压法、安时积分法、内阻法和放电实验法等。

开路电压法具有最高的估计精度，但要求电池充分静置达到平衡状态后才能测量开路电压，无法实现SOC的在线估计［5～6］；安时积分法操作简单，可实现在线估计，但不能确定初值，而且电流传感器受到温度、噪声以及其他扰动的影响，容易出现测量电流值的累积误差而使SOC估计精度降低的现象；内阻法需精确测量电池的内阻值，对测量仪器的要求非常高，而且电池内阻随电池寿命有显著变化，因此仅使用电池内阻难以精确计算SOC值；放电试验法对设备和试验条件的要求高，而且无法在线估计电池SOC；基于模型的方法是以等效电路模型为基准，结合卡尔曼滤波类算法进行估算，所以卡尔曼滤波系列算法对模型依赖程度较高。同时，等效电路模型的参数在估计过程很容易受到电池老化、温度、循环时间、放电率、电压和噪声等因素的影响，会使估算的结果出现较大的误差，且随着电路模型推导的数学模型复杂度的增加，从而产生计算量大等问题；与基于模型的方法不同，数据驱动法对模型精度和环境条件不敏感，不需要建立物理模型，可通过电池电流、电压等数据进行充分训练学习后建立电流、电压和 SOC 的映射关系［7～9］。但该方法通常需要较高的计算成本和较长的处理时间，并且精度在很大程度上取决于训练数据。文献［10］提出了一种遗传算法的BP网络（GA-BP）对蓄电池SOC估算方法。文献［11］将基于遗传算法的径向基函数（GA-RBF）神经网络对锂电池SOC的估算，提高了算法的自适应能力。

针对传统的BP算法容易陷入局部最小点而不是全局最优点，且在实际使用中容易产生梯度消失和爆炸等问题，利用学习速度与泛化性能都更具优势的ESN网络，挖掘电池电流与SOC之间的非线性函数关系，建立了基于ESN网络的SOC预测模型，该方法只需要训练和计算输出权矩阵，减少了计算量。并与其它算法进行了比较分析。最后，通过Matlab软件编程，验证了本文所提方法的可行性。

2 回声状态网络

ESN是由德国H.Jaeger等于2001年首次提出的一种新型的递归神经网络［12］。ESN网络主要由三个部分组成：带输入节点的线性输入层、带神经元的非线性储备池和带输出节点的线性输出层，如图1为回声状态网络结构示意图。其中储备池层由随机生成的、稀疏连接的大量神经元构成。ESN算法突出优点是训练速度快、简单，且输入连接权值和储备池内部连接权值在训练和使用过程中基本不变，因此ESN网络的权值和阈值只需要简单的线性回归即可计算得到，这样能确保其解为全局最优解［13］。

图1 回声状态网络结构示意图

假设系统有K维输入单元、N维内部单元和L维输出单元的ESN网络，通过式（1）来表示n时刻输入矩阵、内部状态矩阵以及输出矩阵。

回声状态网络的内部更新状态如式（2）和式（3）所示。

式中，Win、W、Wback、和Wout分别表示输入、内部连接、输出反馈和输出的权重矩阵，权重矩阵的大小依次为N×K、N×N、N×L和L×(K+L+N)，其中W矩阵是高度稀疏的；表示神经元激活函数；表示输出节点的输出函数，通常是线性函数。

3 回声状态网络的训练过程

ESN神经网络在训练前需要对Win、Wback进行初始化，且在训练和使用过程中基本不变，因此在ESN神经网络学习过程中只需要对输出权重进行训练和调整。以下是具体回声状态网络的建立流程。

1）初始化

在训练ESN神经网络之前需要设置储备池的规模N、谱半径SR、稀疏度SD和输入缩放尺度IS等参数，且这些参数之间没有相关性。此外，还要将输入权值矩阵Win、储备池的内部连接权值矩阵W和输出反馈矩阵Wback进行初始化。

2）训练

在训练阶段中，首先要对训练样本进行预处理；其次使用固定输入权值矩阵Win将输入序列u(n)输入到储备池中，通过固定的储备池连接权值矩阵W稀疏地相互连接，使储备池内部矩阵x(n)通过式（2）更新，最后通过线性函数处理得到网络输出y(n)，如式（3）所示。

为了计算Wout矩阵，需要从m时刻记录内部状态变量和相应的样本数据，并以向量：

构成矩阵B(P-m+1,K+N)，以向量：

构成矩阵T(P-m+1,L)。

由系统状态数据和样本数据，通过线性回归得到输出连接权Wout。由于内部状态变量x(n)与网络实际输出之间为线性关系，故利用网络实际输出逼近网络期望输出y(n)：

out为矩阵Wout的元素）的过程需要保证网络的均方误差最小。则问题转化为求解以下的优化问题：

从数学的观点看，这是一个线性回归问题，可归结为求矩阵B的逆矩阵问题，即Wout=B-1T，至此ESN的训练过程回声状态结束［14］。

3）使用

通过以上ESN神经网络的初始化和训练过程，可直接将输入向量加载到输入节点完成计算，进而在输出节点得到结果。图2为回声状态网络的建立流程。

图2 回声状态网络的建立流程

4 实验测试

通常锂离子电池SOC标准值的获取需要对锂离子电池进行放电实验，然而放电实验法需要对电池做长时间的静置处理，无法进行在线测量，耗费时间较长且充放电电流必须为恒定的值，因此不宜用作仿真参考或在实际工程中应用。为获取电池电压、电流及SOC的值，参考文献［15～16］，本文首先以Matlab/Simulink库中的电池模块为基本元件，以美国环境保护署制定的城市道路循环工况（UDDS工况）下两组不同的放电激励对锂离子电池放电模型进行放电仿真。其中，图3为电池模块验证实验Simulink仿真图。

图3 电池模块验证实验Simulink仿真图

本文所用电池模块的基本参数如下。

E0=3.7V，Q=12Ah，R=0.0056Ω，IC为UDDS工况下两组不同的放电电流，得到电池模块输出电池电流及SOC如表1所示。其中第一组电池电流I对应的SOC估计值如表1的第二列，第二组电池电流I对应的SOC估计值如表1的第四列，两组电流各1000个电流数据点。实验分析中将该SOC值作为实际值SOCS。

本文将表1的两组数据经过筛选，得到了如图4和如图5的两组电池电流和SOC值，两组各800个数据点。

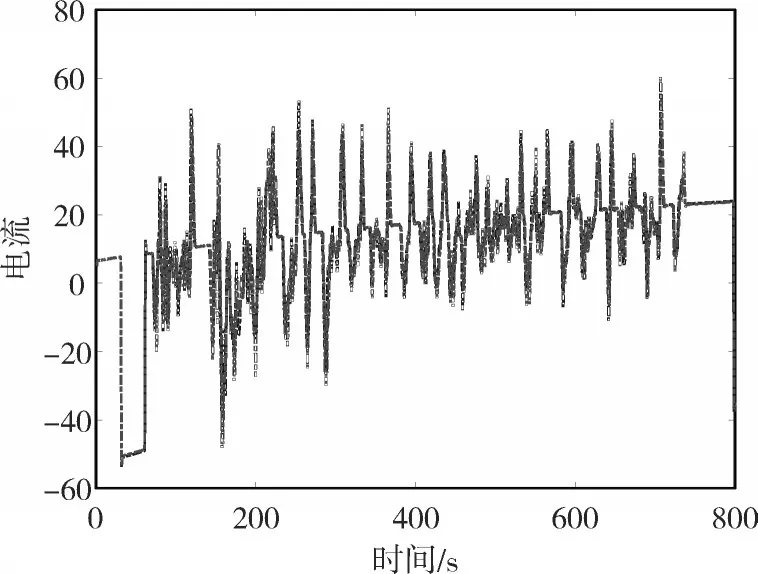
图4 电池电流值

图5 电池SOC值

表1 部分放电试验数据

5 实验结果分析

考虑该网络本身繁琐程度和计算精度，以电池仿真获得数据电流为输入，以SOC为输出，构造基于ESN网络的SOC误差预测模型。根据图4和图5的电流和SOC的值，将其中第一组作为训练集，第二组作为测试集。

为了验证ESN算法构建SOC预测模型方法的有效性，选择合适的输入和输出至关重要。作为典型的非线性时变系统，电池在运行过程中，频繁变化的电流是描述电池动态特性不可或缺的特征量。同时考虑到ESN网络的参数对最终预测性能的影响，本文通过选择得到回声状态网络最优的参数，其中W的稀疏度和谱半径一般选取在1%～5%和［0，1］之间，以及选择2%的稀疏度和矩阵的谱半径为0.6。

在ESN网络中，储备池的大小决定ESN网络的最终预测性能，也反映了网络处理非线性问题的能力。在一定范围内，储备池神经元的数量越多，通过储备池呈现的动态系统越复杂，从而网络的非线性处理能力越强。对于非线性系统，当储备池神经元不足时，网络对系统的非线性预测能力会减弱，从而产生欠拟合现象；当储备池中的神经元数量达到一定数量时，线性拟合能力将不再有明显增强。此时，盲目增加神经元数量会使网络计算复杂化，并会导致神经元过剩和过度拟合现象。因此，储备池神经元数量的选取需要找到一个折中。

图6、图7分别是储备池神经元的数量为50的ESN网络预测模型结果和误差。本文所提出的基于ESN网络的锂离子电池SOC估算方法，前50s预测产生的最大误差比较明显，且具有放大的趋势；与前50s预测产生的最大绝对误差为0.9相比，预测时间到200s时最大绝对误差变为0.39，相比于前50s此预测模型中的最大绝对误差减少了51%；同样与前200s时预测中的最大误差相比，预测时间到600s时，最大绝对误差为0.23，减少了67%；由此可见，随着时间的增加，将大大提高了ESN网络训练的预测效果，同时其误差也逐渐减少。

图6 储备池神经元为50的ESN预测模型结果

图7 储备池神经元为50的ESN预测模型误差

图8、图9分别是储备池神经元数量为200的ESN网络预测模型结果和误差，其最大绝对误差为0.2。根据不同神经元数量的选取得到训练的预测模型的误差可知，随着储备池神经元的数量不断增加，ESN网络预测模型的误差逐渐减少。由此可证明，储备池神经元数量的多少对ESN网络的最终预测性能起着决定作用。

图8 储备池神经元为200的ESN预测模型结果

图9 储备池神经元为200的ESN预测模型误差

为了满足电池SOC估计误差不超过5%的应用需求。本文采用储备池神经元为500的ESN网络预测电池SOC，其结果如图10所示。由图中曲线对比结果可以看出，基于ESN网络预测的电池SOC值更贴近于SOC实际值曲线。图11为ESN网络预测电池SOC的误差，由图中曲线结果可以看出，其最大误差值为0.036，这也证明ESN网络对锂离子电池SOC具有很好的估算能力。

图10 储备池神经元为500的ESN预测模型结果

图11 储备池神经元为500的ESN预测模型误差

表2为储备池不同神经元数量对ESN网络的影响。如表所示，所提出的SOC估算方法，储备池神经元数量为50时的均方根误差、平均绝对误差和平均绝对百分比误差分别是10.65%、7.83%和11.43%，储备池神经元数量为200时，均方根误差、平均绝对误差和平均绝对百分比误差分别是2.21%、1.65%和2.34%，而储备池神经元数量为500时，均方根误差、平均绝对误差和平均绝对百分比误差分别是0.64%、0.44%和0.64%，即在提高神经网络神经元数量的情况下，基于ESN网络的锂离子电池SOC估算方法能够获得较高的精度。

表2 储备池不同神经元数量对ESN网络的影响

为了进一步验证ESN网络的实用性和泛化能力，在相同神经元个数都为500的情况下，采用传统BP神经网络与其对比，图12为BP神经网络SOC预测模型结果。由图中可知，其实际SOC值与ESN网络估算SOC值相差比较大。同时也证明了ESN网络对锂离子电池预测具有较高的精度。

图12 BP神经网络SOC预测模型结果

6 结语

本文建立了基于ESN网络的锂离子电池SOC估算模型，分析储备池中神经元个数为50、200和500对预测结果的影响，验证了神经元数量的增加提高了该模型的对锂离子电池SOC的预测能力。并将此模型与BP神经网络建立的预测模型进行对比，证实了基于ESN网络的SOC预测模型的可行性与优越性。但由于实验环境条件的局限，本文只考虑了电流对锂离子SOC预测模型的影响，未将电池温度等因素考虑在内。下一步的主要工作是考虑多种因素下SOC的建立，提高SOC估计的准确性以确保电池能够安全稳定的运行。