基于多重降噪的轴承故障诊断研究

连雄飞，马 强，王智冲，王宇航，彭 冉

(1.河北工程大学机械与装备工程学院，河北 邯郸 056038； 2.天津大学力学系，天津 300354； 3.河北省智能工业装备技术重点实验室(河北工程大学)，河北 邯郸 056038； 4.天津非线性动力学与控制重点实验室，天津 300354； 5.邯郸熔淬科技有限公司，河北 邯郸 056038)

0 引言

滚动轴承有助于机器平稳高速地旋转，且承载能力好，广泛应用于旋转机械中[1]，但由于运行速度高，易发生故障，导致较大的经济损失，因此及时诊断滚动轴承的早期故障非常必要。

轴承信号中包含的大量状态信息，多表现为非线性和非平稳性信号[2]，这类信号重点在于获得其时域局部性质。处理此类信号时，通常通过时域、频域、时频分析3种方法进行分析[3]，其中时频分析应用更广，本文采用经验模态分解[4]的衍生算法——集合经验模态分解(EEMD)便是一种常用的时频分析方法。

旋转机械装置的复杂结构和环境的多样性，导致轴承故障信号淹没在强背景噪声中，故障信号难以提取。本文针对此问题，提出新的降噪方法，以便提取轴承故障信号。首先利用小波阈值对含噪信号初步去噪，然后利用EEMD将信号分解为多个IMF分量，最后对IMF分量进行SVD分解重构得到最终信号，再通过仿真验证，证明了其较于EEMD-SVD而言能够更好地进行降噪处理。

1 基本理论

1.1 小波阈值去噪

小波变换在信号处理方面具有较好的自适应性[5]，且对于信号处理，小波变换引出多种噪声滤除方法[6]，小波阈值去噪便是其中之一，该方法是由donoho[7]提出的。本文根据轴承振动信号的特征，选择紧支集正交小波(daubechies，db)进行阈值去噪。图1为小波去噪基本原理流程图。

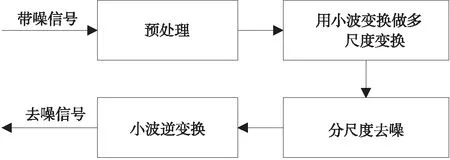
图1 小波去噪流程图

小波阈值降噪(WTD)通过小波变换(WT)对加噪信号s(t)进行分解，并为每个尺度设置小波系数，噪声信号系数相较于待处理信号系数较小，且噪声信号主要分布在高频段[8]，因此选取一个合适的λ值作为阈值对WTD降噪尤为重要。经典阈值函数有2种，其公式分别为：

硬阈值：

(1)

软阈值：

(2)

式中，Wj，k为小波系数，λ为设定阈值，sign(*)为符号函数。

1.2 集合经验模态分解

经验模态分解(EMD)方法处理非线性信号时的一个缺陷就是特征模态函数(IMF)会出现混叠状态，即在分解过程中不同的IMF分量会发生渗透，不同频率会出现在同一IMF分量中，集成经验模态分解算法( EEMD) 则是为了消除、抑制这种混叠状态在EMD的基础上改进而来。已有大量学者将EEMD用于机械振动信号的降噪研究。 EEMD原理是假设在x(t)加入高斯白噪声，对分解得到的IMF分量进行求平均。削减了原信号的间歇性现象，抑制EMD的模态混叠，提高了信号的分解效率和准确性[9]。EEMD 步骤如下。

1)在x(t)中加入高斯白噪声Gi(t)，获得综合信号X1(t) 即:

X1(t)=x(t)+Gi(t)

(3)

2)EMD算法将X1(t)分解得到多个IMF分量。

3)在x(t)中加入不同的噪声，进行(1)(2)步骤N次，求平均，最终得到的IMF 分量:

(4)

式中:xk(t)为对x(t)进行集合经验模态分解得到的第k个IMF分量。

(4)最终，得到原始信号重构信号X(t)。

1.3 奇异值分解

由数学线性理论可知，对于一个实矩阵C，可以构成Hankel矩阵：

(5)

对C进行奇异值分解可得：

C=UΣVT

(6)

U、V为正交矩阵，Σ是奇异值构成的对角矩阵，满足Σ=diag(σ1，σ2，…，σp)、σ1≥σ2≥…≥σp≥0[10]。C为待处理矩阵，左右奇异向量分别由U、V列向量组成。奇异值分解具有良好的尺度和稳定性，也是矩阵固有的特征。U、V满足条件：UUT=I、VVT=I、p=min(m，n)。利用信号能量的可分性，选择合适奇异值，按照式(5)进行SVD逆变换，得到降噪后信号。

2 WTD-EEMD-SVD多重降噪处理

2.1 筛选IMF分量

本文选择了相关系数法作为EEMD分解后IMF分量筛选的依据。相关系数计算为：

(7)

式中：y(i)为相关系数；IMFi为第i个IMF分量。

2.2 降噪处理过程

获得相关系数后，针对上述人为挑选IMF分量所存在的问题，设计提出了 WTD-EEMD-SVD多层联合降噪处理方法，流程如图2所示。

图2 基于WTD-EEMD-SVD降噪流程图

3 仿真验证

为验证所提降噪方法的有效性，引入含噪信号进行MATLAB仿真。

构建原始信号数学模型x(t)=sin(2π·25t)+sin(2π·60t)，加噪信号s(t)=x(t)+n(t)，采样频率fs=1 024 Hz，采样长度N=1 024，n(t)为高斯白噪声。图3和图4分别为x(t)和s(t)的时域波形和频域图，图中可看出频率已被噪声淹没。

本文方法首先对s(t)采用‘db4’小波基函数进行WTD软阈值降噪并重构信号s1(t)，得到降噪信号时域图与频域图，如图5所示。

对s1(t)进行EEMD分解得到图6、图7的IMF分量时域频域图，通过式(7)计算每个IMF分量对应的相关系数，挑选合适的IMF分量。

图3 原始信号时域图与频域图

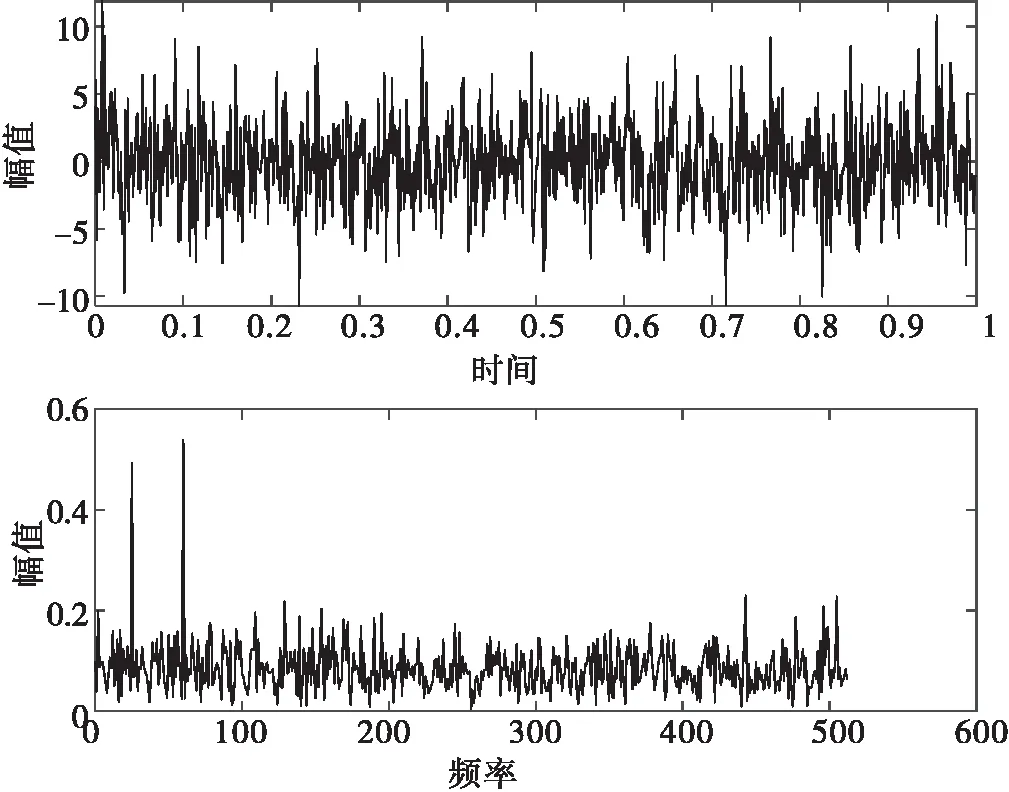
图4 加噪信号时域图与频域图

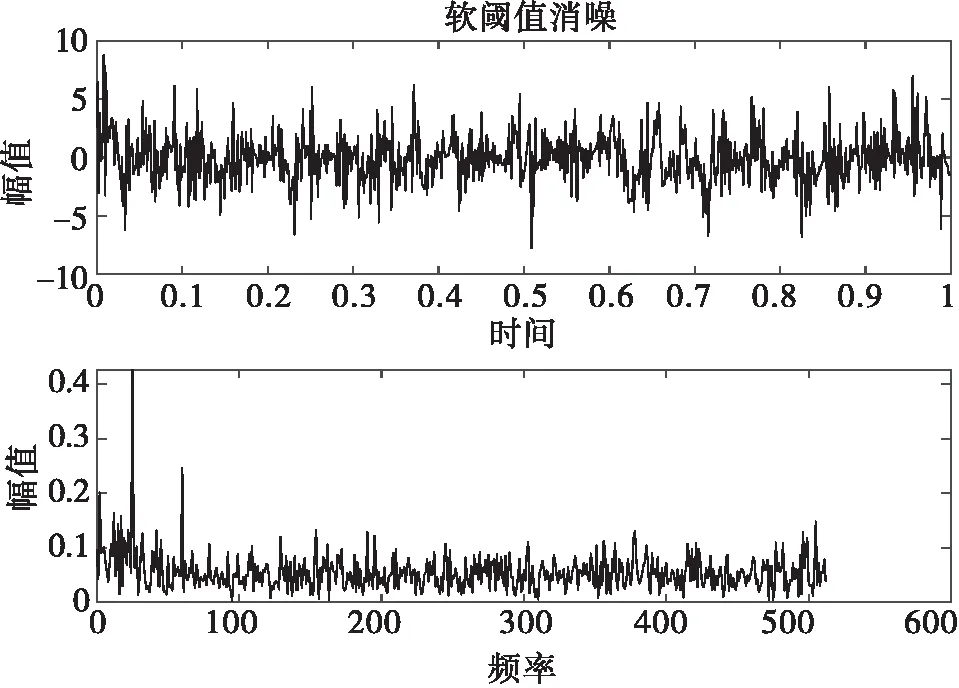
图5 小波软阈值去噪时域图与频域图

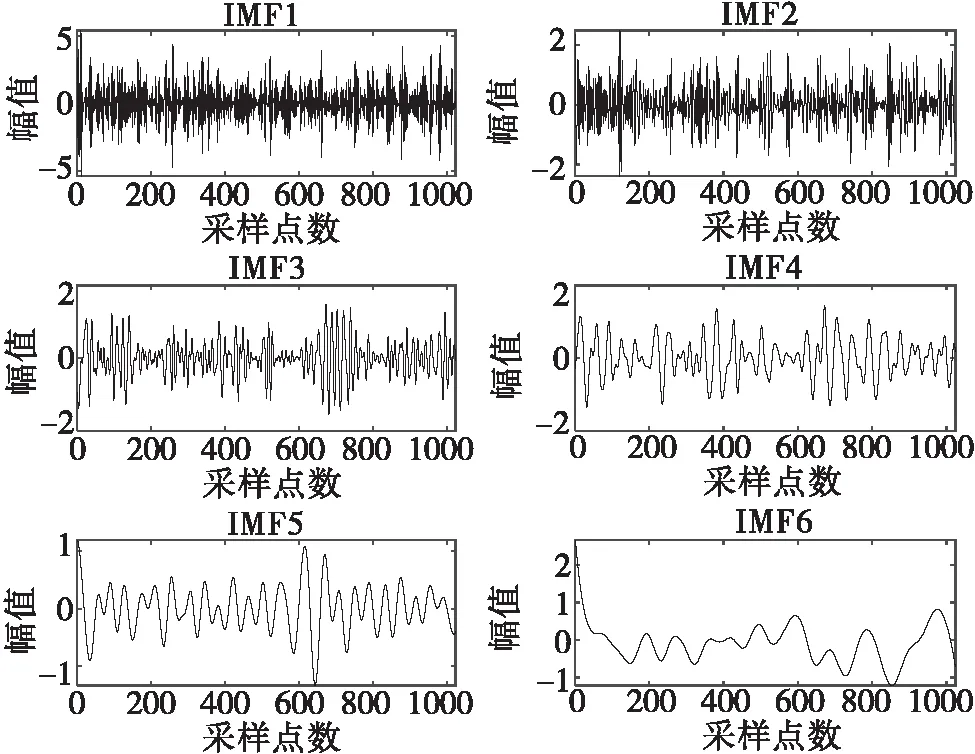
图6 IMF分量时域图

图7 IMF分量频域图

最后对上述降噪结果进行SVD分解，得WTD-EEMD-SVD 多重降噪信号，时域图与频谱图如图8所示，能明显看出时域中噪声减弱，波形与原始信号波形相近。频域图中大量干扰频率已被去除，特征频率出现，降噪效果明显。

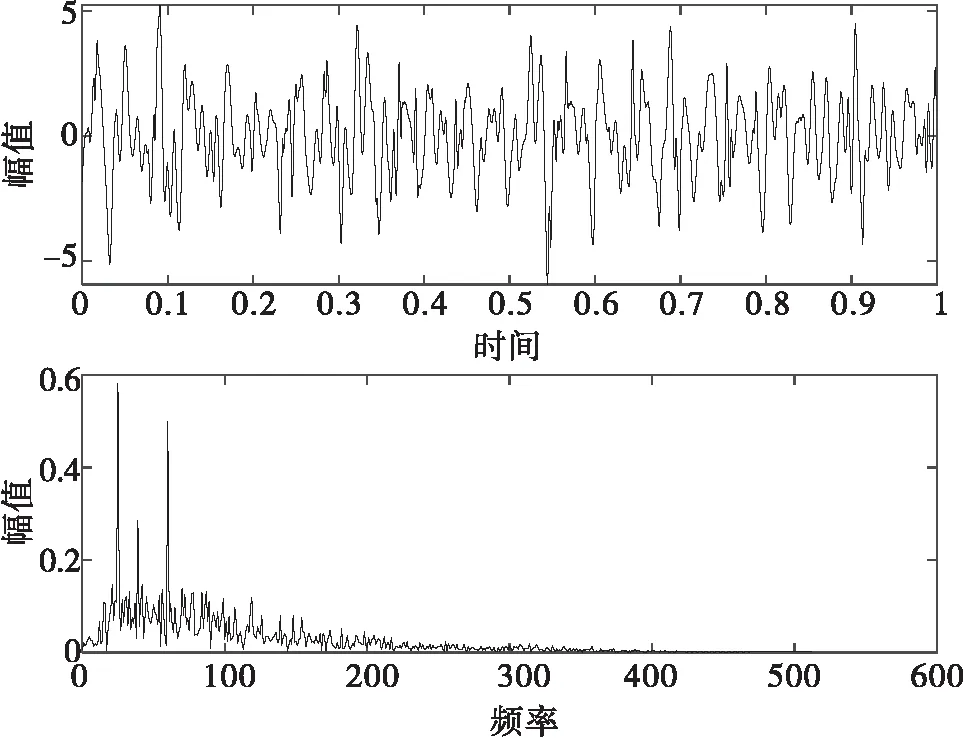
图8 WTD-EEMD-SVD降噪时域图与频域图

相关系数如表1所示，前4个IMF的相关系数远大于其他IMF值，其包含的噪声信号成分最多，有效信息较多，保留；剩余分量的相关系数较低，舍去。

表1 各IMF分量的相关系数值

本文采用EEMD-SVD方法作了对比，并进行验证，结果如图9所示。为体现降噪效果引入信噪比作为分析指标，得出了表2。

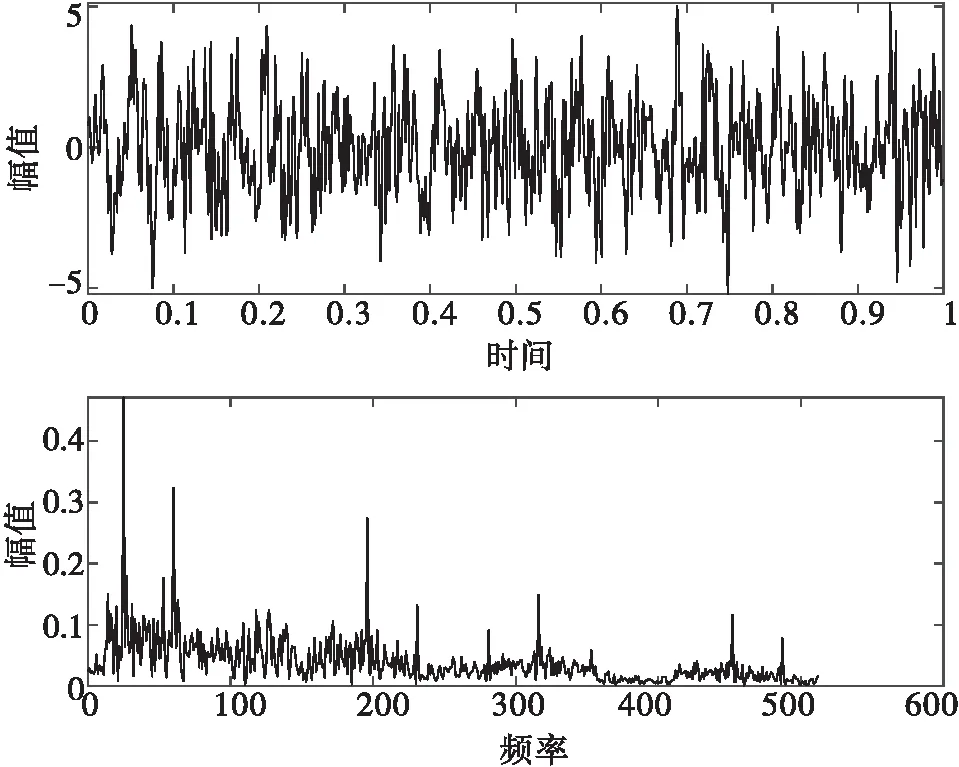
图9 EEMD-SVD降噪时域图与频域图

表2 降噪方法对比

通过对比表2信噪比可以看出，WTD-EEMD-SVD算法能够有效滤除随机噪声，凸显频率特征，是一种更优的降噪处理方法。

4 实例分析

为验证WTD-EEMD-SVD方法在轴承故障信号中降噪效果，采用美国西储大学数据进行试验，试验轴承型号为：SKF6205-2RS深沟球轴承，尺寸如表3所示，图10为西储大学轴承实验设备。

表3 SKF6205-2RS轴承尺寸数据

为简洁地展示降噪效果，选取内圈故障的轴承的实验数据进行处理。依据公式(8)计算出理论内圈故障频率为162.1 Hz。

(8)

图10 西储大学轴承实验设备

图11为降噪处理前轴承数据的时域图、包络谱图。由图可知，轴承数据中存在振动噪声，对后期的故障诊断造成干扰。经过 WTD-EEMD-SVD联合降噪处理后得到图12，明显去除了大部分噪声信号，且由包络谱图可看到故障特征频率和二倍频更加明显，验证了通过本文提出的降噪预处理方法提取故障频率的有效性。

图11 采样信号

图12 WTD-EEMD-SVD多重降噪

5 结论

1)对比分析了EEMD-SVD去噪方法，通过对比去噪后的信噪比，验证了本文提出方法能够更好地滤除振动信号中的噪声，是一种更优的降噪方法。

2)提出了一种基于WTD-EEMD-SVD的联合降噪方法。首先经过小波软阈值降噪得到第一重降噪信号，然后充分发挥EEMD分解的优点，挑选出合适IMF分量，再利用SVD进行分解降噪，最终对降噪后信号包络谱分析，有效地完成了信号降噪。